The Project Gutenberg eBook of Extra-galactic nebulae, by Edwin Hubble
This eBook is for the use of anyone anywhere in the United States and
most other parts of the world at no cost and with almost no restrictions
whatsoever. You may copy it, give it away or re-use it under the terms
of the Project Gutenberg License included with this eBook or online
at
www.gutenberg.org. If you
are not located in the United States, you will have to check the laws of the
country where you are located before using this eBook.
Title: Extra-galactic nebulae
Author: Edwin Hubble
Release Date: June 29, 2022 [eBook #68428]
Language: English
Produced by: Anonymous (This book was produced from images made available by the HathiTrust Digital Library.)
*** START OF THE PROJECT GUTENBERG EBOOK EXTRA-GALACTIC NEBULAE ***
Transcriber’s Note
Cover image was created by transcriber using an image of the irregular
nebula N.G.C. 4214 contained in Plate XIV. The cover is placed into the
public domain.
EXTRA-GALACTIC NEBULAE1
By EDWIN HUBBLE
[Transcriber’s Note: This etext was produced from
The Astrophysical Journal, Vol. LXIV, pp. 321-369, 1926.]
ABSTRACT
This contribution gives the results of a statistical investigation of
400 extra-galactic nebulae for which Holetschek has determined total
visual magnitudes. The list is complete for the brighter nebulae in the
northern sky and is representative to 12.5 mag. or fainter.
The classification employed is based on the forms of the photographic
images. About 3 per cent are irregular, but the remaining nebulae fall
into a sequence of type forms characterized by rotational symmetry
about dominating nuclei. The sequence is composed of two sections, the
elliptical nebulae and the spirals, which merge into each other.
Luminosity relations.—The distribution of magnitudes appears to
be uniform throughout the sequence. For each type or stage in the
sequence, the total magnitudes are related to the logarithms of the
maximum diameters by the formula,
 where C varies progressively from type to type, indicating a variation
in diameter for a given magnitude or vice versa. By applying
corrections to C, the nebulae can be reduced to a standard type and
then a single formula expresses the relation for all nebulae from
the Magellanic Clouds to the faintest that can be classified. When
the minor diameter is used, the value of C is approximately constant
throughout the entire sequence. The coefficient of log d corresponds
with the inverse-square law, which suggests that the nebulae are all of
the same order of absolute luminosity and that apparent magnitudes are
measures of distance. This hypothesis is supported by similar results
for the nuclear magnitudes and the magnitudes of the brightest stars
involved, and by the small range in luminosities among nebulae whose
distances are already known.
where C varies progressively from type to type, indicating a variation
in diameter for a given magnitude or vice versa. By applying
corrections to C, the nebulae can be reduced to a standard type and
then a single formula expresses the relation for all nebulae from
the Magellanic Clouds to the faintest that can be classified. When
the minor diameter is used, the value of C is approximately constant
throughout the entire sequence. The coefficient of log d corresponds
with the inverse-square law, which suggests that the nebulae are all of
the same order of absolute luminosity and that apparent magnitudes are
measures of distance. This hypothesis is supported by similar results
for the nuclear magnitudes and the magnitudes of the brightest stars
involved, and by the small range in luminosities among nebulae whose
distances are already known.
Distances and absolute dimensions.—The mean absolute visual
magnitude, as derived from the nebulae whose distances are known, is
–15.2. The statistical expression for the distance in parsecs is then
 where mT is the total apparent magnitude. This leads to mean values
for absolute dimensions at various stages in the sequence of types.
Masses appear to be of the order of 2.6×108 ☉.
where mT is the total apparent magnitude. This leads to mean values
for absolute dimensions at various stages in the sequence of types.
Masses appear to be of the order of 2.6×108 ☉.
Distribution and density of space.—To apparent magnitude about
16.7, corresponding to an exposure of one hour on fast plates with
the 60-inch reflector, the numbers of nebulae to various limits of
total magnitude vary directly with the volumes of space represented
by the limits. This indicates an approximately uniform density of
space, of the order of one nebula per 1017 cubic parsecs or 1.5×10–31
in C.G.S. units. The corresponding radius of curvature of the
finite universe of general relativity is of the order of 2.7×1010
parsecs, or about 600 times the distance at which normal nebulae can be
detected with the 100-inch reflector.
Recent studies have emphasized the fundamental nature of the division
between galactic and extra-galactic nebulae. The relationship is not
generic; it is rather that of the part to the whole. Galactic{2} nebulae
are clouds of dust and gas mingled with the stars of a particular
stellar system; extra-galactic nebulae, at least the most conspicuous
of them, are now recognized as systems complete in themselves, and
often incorporate clouds of galactic nebulosity as component parts of
their organization. Definite evidence as to distances and dimensions is
restricted to six systems, including the Magellanic Clouds. The similar
nature of the countless fainter nebulae has been inferred from the
general principle of the uniformity of nature.
The extra-galactic nebulae form a homogeneous group in which numbers
increase rapidly with diminishing apparent size and luminosity. Four
are visible to the naked eye;2 41 are found on the Harvard “Sky
Map”;3 700 are on the Franklin-Adams plates;4 300,000 are estimated
to be within the limits of an hour’s exposure with the 60-inch
reflector.5 These data indicate a wide range in distance or in
absolute dimensions. The present paper, to which is prefaced a general
classification of nebulae, discusses such observational material as we
now possess in an attempt to determine the relative importance of these
two factors, distance and absolute dimensions, in their bearing on the
appearance of extra-galactic nebulae.
The classification of these nebulae is based on structure, the
individual members of a class differing only in apparent size and
luminosity. It is found that for the nebulae in each class these
characteristics are related in a manner which closely approximates
the operation of the inverse-square law on comparable objects. The
presumption is that dispersion in absolute dimensions is relatively
unimportant, and hence that in a statistical sense the apparent
dimensions represent relative distances. The relative distances can be
reduced to absolute values with the aid of the nebulae whose distances
are already known.
PART I. CLASSIFICATION OF NEBULAE
GENERAL CLASSIFICATION
The classification used in the present investigation is essentially
the detailed formulation of a preliminary classification published
in{3} a previous paper.6 It was developed in 1923, from a study of
photographs of several thousand nebulae, including practically all
the brighter objects and a thoroughly representative collection of
the fainter ones.7 It is based primarily on the structural forms of
photographic images, although the forms divide themselves naturally
into two groups: those found in or near the Milky Way and those in
moderate or high galactic latitudes. In so far as possible, the system
is independent of the orientation of the objects in space. With minor
changes in the original notation, the complete classification is as
follows, although only the extra-galactic division is here discussed in
detail:
CLASSIFICATION OF NEBULAE
|
|
Symbol |
Example |
| I. |
Galactic nebulae: |
|
|
|
A. |
Planetaries |
P |
N.G.C. 7662 |
|
B. |
Diffuse |
D |
|
|
|
1. |
Predominantly luminous |
DL |
N.G.C. 6618 |
|
|
2. |
Predominantly obscure |
DO |
Barnard 92 |
|
|
3. |
Conspicuously mixed |
DLO |
N.G.C. 7023 |
| II. |
Extra-galactic nebulae: |
|
|
|
A. |
Regular: |
|
|
|
|
1. |
Elliptical
(n=1, 2, ..., 7 indicates the ellipticity
of the image without the decimal point) |
En |
N.G.C. 3379 E0
N.G.C. 221 E2
N.G.C. 4621 E5
N.G.C. 2117 E7{4} |
|
|
2. |
Spirals: |
|
|
|
|
|
|
a) |
Normal spirals |
S |
|
|
|
|
|
|
(1) Early |
Sa |
N.G.C. 4594 |
|
|
|
|
|
(2) Intermediate |
Sb |
N.G.C. 2841 |
|
|
|
|
|
(3) Late |
Sc |
N.G.C. 5457 |
|
|
|
|
b) |
Barred spirals |
SB |
|
|
|
|
|
|
(1) Early |
SBa |
N.G.C. 2859 |
|
|
|
|
|
(2) Intermediate |
SBb |
N.G.C. 3351 |
|
|
|
|
|
(3) Late |
SBc |
N.G.C. 7479 |
|
B. |
Irregular |
Irr |
N.G.C. 4449 |
Extra-galactic nebulae too faint to be classified are designated
by the symbol “Q.”
REGULAR NEBULAE
The characteristic feature of extra-galactic nebulae is rotational
symmetry about dominating non-stellar nuclei. About 97 per cent of
these nebulae are regular in the sense that they show this feature
conspicuously. The regular nebulae fall into a progressive sequence
ranging from globular masses of unresolved nebulosity to widely open
spirals whose arms are swarming with stars. The sequence comprises two
sections, elliptical nebulae and spirals, which merge into each other.
Although deliberate effort was made to find a descriptive
classification which should be entirely independent of theoretical
considerations, the results are almost identical with the path of
development derived by Jeans8 from purely theoretical investigations.
The agreement is very suggestive in view of the wide field covered by
the data, and Jeans’s theory might have been used both to interpret
the observations and to guide research. It should be borne in mind,
however, that the basis of the classification is descriptive and
entirely independent of any theory.
Elliptical nebulae.—These give images ranging from circular
through flattening ellipses to a limiting lenticular figure in which
the ratio of the axes is about 1 to 3 or 4. They show no evidence
of resolution,9 and the only claim to structure is that the
luminosity{5} fades smoothly from bright nuclei to indefinite edges.
Diameters are functions of the nuclear brightness and the exposure
times.
PLATE XII

E0 NGC 3379

E2 NGC 221 (M 32)

E5 NGC 4621 (M 59)

E7 NGC 3115

NGC 3034 (M 82),

NGC 4449
Elliptical and Irregular Nebulae
The only criterion available for further classification appears to
be the degree of elongation. Elliptical nebulae have accordingly been
designated by the symbol “E,” followed by a single figure, numerically
equal to the ellipticity (a – b)/a with the decimal point omitted.
The complete series is E0, E1, ..., E7, the last representing
a definite limiting figure which marks the junction with the
spirals.
The frequency distribution of ellipticities shows more round or nearly
round images than can be accounted for by the random orientation of
disk-shaped objects alone. It is presumed, therefore, that the images
represent nebulae ranging from globular to lenticular, oriented at
random. No simple method has yet been established for differentiating
the actual from the projected figure of an individual object, although
refined investigation furnishes a criterion in the relation between
nuclear brightness and maximum diameters. For the present, however,
it must be realized that any list of nebulae having a given apparent
ellipticity will include a number of tilted objects having greater
actual ellipticities. The statistical average will be too low, except
for E7, and the error will increase with decreasing ellipticity.
Normal spirals.—All regular nebulae with ellipticities greater than
about E7 are spirals, and no spirals are known with ellipticities less
than this limit. At this point in the sequence, however, ellipticity
becomes insensitive as a criterion and is replaced by conspicuous
structural features which now become available for classification. Of
these, practically speaking, there are three which fix the position of
an object in the sequence of forms: (1) relative size of the unresolved
nuclear region; (2) extent to which the arms are unwound; (3) degree of
resolution in the arms. The form most nearly related to the elliptical
nebulae has a large nuclear region similar to E7, around which are
closely coiled arms of unresolved nebulosity. Then follow objects in
which the arms appear to build up at the expense of the nuclear regions
and unwind as they grow; in the end, the arms are wide open and the
nuclei inconspicuous. Early in the series the arms begin to break up
into condensations, the resolution{6} commencing in the outer regions
and working inward until in the final stages it reaches the nucleus
itself. In the larger spirals where critical observations are possible,
these condensations are found to be actual stars and groups of stars.
The structural transition is so smooth and continuous that the
selection of division points for further classification is rather
arbitrary. The ends of the series are unmistakable, however, and, in
a general way, it is possible to differentiate a middle group. These
three groups are designated by the non-committal letters “a,” “b,” and
“c” attached to the spiral symbols “S,” and, with reference to their
position in the sequence, are called “early,” “intermediate,” and
“late” types.10 A more precise subdivision, on a decimal scale for
example, is not justified in the present state of our knowledge.
In the early types, the group Sa, most of the nebulosity is in the
nuclear region and the arms are closely coiled and unresolved. N.G.C.
3368 and 4274 are among the latest of this group.
The intermediate group, Sb, includes objects having relatively large
nuclear regions and thin rather open arms, as in M 81, or a smaller
nuclear region with closely coiled arms, as in M 94. These two nebulae
represent the lateral extension of the sequence in the intermediate
section. The extension along the sequence is approximately represented
by N.G.C. 4826, among the earliest of the Sb, and N.G.C. 3556 and
7331, which are among the latest. The resolution in the arms is seldom
conspicuous, although in M 31, a typical Sb, it is very pronounced in
the outer portions.
PLATE XIII
Sa NGC 4594

SBa NGC 2859

Sb NGC 2841

SBb NGC 5850

Sc NGC 5457 (M 101),

SBc NGC 7479
Normal and Barred Spirals
{7}
The characteristics of the late types, the group Sc, are more
definite—an inconspicuous nucleus and highly resolved arms. Individual
stars cannot be seen in the smaller nebulae of this group, but knots
are conspicuous, which, in larger objects, are known to be groups and
clusters of stars. The extent to which the arms are opened varies from
M 33 to M 101, both typical Sc nebulae.
Barred spirals.—In the normal spiral the arms emerge from two
opposite points on the periphery of the nuclear region. There is,
however, a smaller group, containing about 20 per cent of all spirals,
in which a bar of nebulosity extends diametrically across the nucleus.
In these spirals, the arms spring abruptly from the ends of this
bar. These nebulae also form a sequence, which parallels that of the
normal spirals, the arms apparently unwind, the nuclei dwindle, the
condensations form and work inward.
H. D. Curtis11 first called attention to these nebulae when he
described several in the intermediate stages of the series and called
them φ-type spirals. The bar, however, never extends beyond the inner
spiral arms, and the structure, especially in the early portion of the
sequence, is more accurately represented by the Greek letter θ. From a
dynamical point of view, the distinction has considerable significance.
Since Greek letters are inconvenient for cataloguing purposes, the
English term, “barred spiral,” is proposed, which can be contracted to
the symbol “SB.”
The SB series, like that of the normal spirals, is divided into three
roughly equal sections, distinguished by the appended letters “a,”
“b,” and “c.” The criteria on which the division is based are similar
in general to those used in the classification of the normal spirals.
In the earliest forms, SBa, the arms are not differentiated, and
the pattern is that of a circle crossed by a bar, or, as has been
mentioned, that of the Greek letter θ. When the bar is oriented nearly
in the line of sight, it appears foreshortened as a bright and definite
minor axis of the elongated nebular image. Such curious forms as the
images of N.G.C. 1023 and 3384 are explained in this manner. The latest
group, SBc, is represented by the S-shaped spirals such as N.G.C. 7479.
{8}
IRREGULAR NEBULAE
About 3 per cent of the extra-galactic nebulae lack both dominating
nuclei and rotational symmetry. These form a distinct class which can
be termed “irregular.” The Magellanic Clouds are the most conspicuous
examples, and, indeed, are the nearest of all the extra-galactic
nebulae. N.G.C. 6822, a curiously faithful miniature of the Clouds,
serves to bridge the gap between them and the smaller objects, such as
N.G.C. 4214 and 4449. In these latter, a few individual stars emerge
from an unresolved background, and occasional isolated spots give the
emission spectrum characteristic of diffuse nebulosity in the galactic
system, in the Clouds, and in N.G.C. 682212 These features are found
in other irregular nebulae as well, notably in N.G.C. 1156 and 4656,
and are just those to be expected in systems similar to the Clouds but
situated at increasingly greater distances.
The system outlined above is primarily for the formal classification of
photographic images obtained with large reflectors and portrait lenses.
For each instrument, however, there is a limiting size and luminosity
below which it is impossible to classify with any confidence. Except
in rare instances, these small nebulae are extra-galactic, and their
numbers, brightness, dimensions, and distribution are amenable to
statistical investigation. For cataloguing purposes, they require a
designating symbol, and the letter “Q” is suggested as convenient and
not too widely used with other significations.
PLATE XIV

Direct photograph with 100-inch reflector March 18, 1925. Scale 1 mm = 3″.3

Slitless spectrogram at primary focus of 100-inch reflector, March 19, 1925
Irregular Nebula N.G.C. 4214
PART II. STATISTICAL STUDY OF EXTRA-GALACTIC NEBULAE
THE DATA
The most homogeneous list of nebulae for statistical study is that
compiled by Hardcastle13 containing all nebulae found on the
Franklin-Adams charts. These are uniform exposures of two hours on
fast plates made with a Cooke astrographic lens of 10-inch aperture
and 45-inch focal length. The scale is 1 mm = 3′. The entire sky is
covered,{9} but since the plates are centered about 15° apart and the
definition decreases very appreciably with distance from the optical
axis, the material is not strictly homogeneous. Moreover, the published
list suffers from the usual errors attendant on routine cataloguing;
for instance, four conspicuous Messier nebulae, M 60, M 87, M 94,
and M 101, are missing. In general, however, the list is thoroughly
representative down to about the thirteenth photographic magnitude and
very few conspicuous objects are overlooked. It plays the role of a
standard with which other catalogues of the brighter nebulae may be
compared for completeness, and numbers in limited areas may be extended
to the entire sky.
When known galactic nebulae, clusters, and the objects in the
Magellanic Clouds are weeded out, the remaining 700 nebulae may
be treated as extra-galactic. Very few can be classified from the
Franklin-Adams plates; for this purpose photographs on a much larger
scale are required. Until further data on the individual objects
are available, Hardcastle’s list can be used only for the study of
distribution over the sky. This shows the well-known features—the
greater density in the northern galactic hemisphere, the concentration
in Virgo, and the restriction of the very large nebulae to the southern
galactic hemisphere.
Fortunately, numerical data do exist in the form of total visual
magnitudes for many of the nebulae in the northern sky. These
determinations were made by Holetschek,14 who attempted to observe
all nebulae within reach of his 6-inch refractor. He later restricted
his program; but the final list is reasonably complete for the more
conspicuous nebulae north of declination –10°, and is representative
down to visual magnitude about 12.5. Out of 417 extra-galactic nebulae
in Holetschek’s list, 408 are north of –10°, as compared with 400
in Hardcastle’s. The two lists agree very well for the brighter
objects, but diverge more and more with decreasing luminosity. At the
twelfth magnitude about half of Holetschek’s nebulae are included by
Hardcastle. Since the two lists compare favorably in completeness over
so large a region of the sky, Holetschek’s may be chosen as the basis
for a statistical study and advantage taken of the valuable numerical
data on total luminosities.
{10}
Hopmann15 has revised the scale of magnitudes by photometric measures
of the comparison stars used by Holetschek. New magnitudes were thus
obtained for 85 individual nebulae and from these were derived mean
correction tables applicable to the entire list. The revised magnitudes
are used throughout the following discussion. Hopmann’s corrections
extend to about 12.0 mag., and have been extrapolated on the assumption
that they are constant for the fainter magnitudes. The errors involved
are unimportant in view of selective effects which must be present
among the observed objects near the limit of visibility.
The nebulae were classified and their diameters measured from
photographs of about 300 of them taken with the 60-inch and 100-inch
reflectors at Mount Wilson. Most of the others are included in the
great collection of nebular photographs at Mount Hamilton, which
have been described by Curtis;16 and, through the courtesy of the
Director of the Lick Observatory, it has been possible to confirm
the classification inferred from the published description by actual
inspection of the original negatives.
Types, diameters, and total visual magnitudes are thus available for
some 400 of the nebulae in Holetschek’s list. The few unclassified
objects are all fainter than 12.5 mag. The data are listed in Tables
I–IV, in which the N.G.C. numbers, the total magnitudes, and the
logarithms of the maximum diameters in minutes of arc are given for
each type separately. A summary is given in Table V, in which the
relative frequencies and the mean magnitudes of the various types will
be found.
RELATIVE LUMINOSITIES OF THE VARIOUS TYPES
The frequency distribution of magnitudes for all types together and for
the elliptical nebulae and the spirals separately is shown in Table VI
and Figure 1. With the exception of the two outstanding spirals, M 31
and M 33, the apparent luminosities are about uniformly distributed
among the different types. The relative numbers of the elliptical
nebulae as compared with the spirals decrease somewhat with decreasing
luminosity, but this is very probably an effect{11} of selection.
The elliptical nebulae are more compact than the spirals and become
more stellar with decreasing luminosity. For this reason some of the
fainter nebulae are missed when small-scale instruments are used,
although the same luminosity spread over a larger area would still be
easily detected. The effect is very pronounced on photographic plates.
It accounts also for the slightly brighter mean magnitude of the
elliptical nebulae as compared with the spirals in Table V.
TABLE I
Elliptical Nebulae
| N.G.C. |
mT |
log d |
| E0 (17) |
| 404 |
11.1 |
+0.11 |
| 474 |
12.6 |
– .40 |
| 1407 |
10.9 |
.15 |
| 3348 |
11.8 |
– .15 |
| 3379* |
9.4 |
+ .30 |
| 4283 |
12.2 |
– .52 |
| 4486* |
9.7 |
+ .30 |
| 4494* |
10.1 |
– .15 |
| 4552* |
9.9 |
+ .23 |
| 4589 |
11.4 |
– .30 |
| 4648 |
12.3 |
.52 |
| 5044 |
11.8 |
.30 |
| 5216 |
13.3 |
.70 |
| 5273 |
12.1 |
.52 |
| 5557 |
12.3 |
.40 |
| 5812 |
12.0 |
– .40 |
| 5846 |
10.9 |
0.0 |
| Mean |
11.40 |
–0.204 |
| E1 (13) |
| 467 |
13.0 |
–0.70 |
| 596 |
11.8 |
.22 |
| 1400 |
11.1 |
.22 |
| 2880 |
12.0 |
.52 |
| 3226 |
12.0 |
.10 |
| 3962 |
11.8 |
– .30 |
| 4278* |
10.8 |
.0 |
| 4374* |
9.9 |
+ .08 |
| 4472 |
8.8 |
+ .30 |
| 4478 |
11.5 |
– .10 |
| 4636 |
10.9 |
+ .08 |
| 5813 |
12.6 |
– .30 |
| 7626 |
12.3 |
–0.30 |
| Mean |
11.43 |
–0.177 |
| E2 (14) |
| 221* |
8.8 |
+0.42 |
| 1453 |
11.9 |
– .10 |
| 2672 |
12.8 |
– .40 |
| 3193 |
12.1 |
0.0 |
| 3599 |
12.0 |
–0.30 |
| 3608 |
11.6 |
.22 |
| 3640 |
11.1 |
– .05 |
| 4261 |
11.1 |
+ .20 |
| 4291 |
12.3 |
– .52 |
| 4377 |
11.9 |
– .05 |
| 4406* |
10.0 |
+ .30 |
| 4476 |
12.8 |
– .30 |
| 4649* |
9.5 |
+ .30 |
| 5127 |
13.3 |
–0.52 |
| Mean |
11.52 |
–0.088 |
| E3 (10) |
| 1052 |
11.8 |
–0.15 |
| 1600 |
12.7 |
+ .17 |
| 3222 |
13.3 |
– .15 |
| 4319 |
12.8 |
– .52 |
| 4365 |
11.4 |
+ .04 |
| 4386 |
12.3 |
– .52 |
| 5322* |
9.6 |
+ .15 |
| 5982 |
11.4 |
.0 |
| 7562 |
12.8 |
– .22 |
| 7619 |
11.8 |
– .15 |
| Mean |
11.99 |
–0.133 |
| E4 (13) |
| 584 |
10.9 |
+0.30 |
| 1700 |
12.5 |
– .10 |
| 2974 |
11.8 |
.15 |
| 3605 |
12.5 |
– .52 |
| 3610 |
11.8 |
+ .15 |
| 3894 |
12.8 |
– .05 |
| 4125* |
10.3 |
+ .30 |
| 4378 |
12.1 |
– .15 |
| 4382* |
10.0 |
+ .48 |
| 4551 |
12.8 |
+ .04 |
| 4742 |
12.3 |
.0 |
| 5576 |
12.3 |
– .15 |
| 7454 |
13.3 |
0.0 |
| Mean |
11.95 |
–0.011 |
| E5 (6){12} |
| 720 |
10.9 |
+ .11 |
| 2693 |
12.3 |
– .15 |
| 3377 |
10.9 |
+ .17 |
| 4473 |
10.3 |
.11 |
| 4621* |
10.0 |
+ .30 |
| 4660 |
11.4 |
0.0 |
| Mean |
10.97 |
+0.090 |
| E6 (7) |
| 821 |
11.8 |
0.0 |
| 2768 |
10.7 |
+ .18 |
| 3613 |
11.8 |
.25 |
| 4179 |
11.8 |
.34 |
| 4435* |
10.5 |
.11 |
| 4546* |
10.3 |
.18 |
| 4697* |
9.6 |
+0.48 |
| Mean |
10.93 |
+0.220 |
| E7 (5) |
| 3115* |
9.5 |
+0.60 |
| 4111 |
10.1 |
.54 |
| 4270 |
12.1 |
.0 |
| 4570 |
11.1 |
.38 |
| 5308 |
12.3 |
+0.28 |
| Mean |
11.02 |
+0.360 |
| Peculiar (8) |
| 185 |
12.3 |
+0.48 |
| 205* |
9.3 |
.90 |
| 524† |
11.9 |
.41 |
| 3607† |
9.9 |
.11 |
| 3998† |
12.1 |
+ .23 |
| 4459‡ |
11.3 |
– .22 |
| 5485‡ |
12.3 |
.05 |
| 5739 |
13.3 |
–0.40 |
The various types are homogeneously distributed over the sky, their
spectra are similar, and the radial velocities are of the same general
order. These facts, together with the equality of the mean magnitudes
and the uniform frequency distribution of magnitudes, are consistent
with the hypothesis that the distances and absolute luminosities
as well are of the same order for the different types. This is an
assumption of considerable importance, but unfortunately it cannot yet
be subjected to positive and definite tests. None of the individual
similarities necessarily implies the adopted interpretation, but the
totality of them, together with the intimate series relations{13} among
the types, which will be discussed later, suggests it as the most
reasonable working hypothesis, at least until inconsistencies should
appear.
TABLE II
Barred Spirals
| N.G.C. |
mT |
log d |
| SBa (26) |
| 936 |
11.1 |
+0.48 |
| 1023* |
10.2 |
.78 |
| 2732 |
12.3 |
.11 |
| 2781 |
12.3 |
.11 |
| 2787 |
11.4 |
.36 |
| 2859 |
11.1 |
.28 |
| 2950 |
11.6 |
.15 |
| 3384* |
10.7 |
.48 |
| 3412* |
11.2 |
+ .40 |
| 3418 |
13.1 |
.0 |
| 3458 |
12.8 |
– .22 |
| 3945 |
11.5 |
+ .20 |
| 4026 |
11.1 |
.48 |
| 4203 |
11.1 |
.36 |
| 4346 |
12.0 |
.20 |
| 4371 |
12.0 |
.18 |
| 4421 |
12.8 |
.17 |
| 4442 |
10.9 |
.50 |
| 4477 |
10.9 |
.40 |
| 4596 |
12.0 |
.25 |
| 4643 |
11.1 |
.26 |
| 4754 |
10.9 |
.48 |
| 5473 |
12.0 |
+ .08 |
| 5574 |
13.0 |
– .05 |
| 5689 |
12.0 |
+ .30 |
| 5701 |
12.3 |
+0.17 |
| Mean |
11.66 |
+0.267 |
| SBb (16) |
| 1022 |
11.8 |
+0.04 |
| 2650 |
12.8 |
.0 |
| 3351* |
11.4 |
+ .48 |
| 3400 |
12.5 |
– .10 |
| 3414 |
11.5 |
+ .26 |
| 3504 |
11.4 |
.30 |
| 3718 |
11.8 |
+0.48 |
| 4102 |
12.0 |
+0.36 |
| 4245 |
11.1 |
.15 |
| 4394 |
11.5 |
.60 |
| 4548 |
11.1 |
.60 |
| 4699* |
10.0 |
.57 |
| 4725* |
9.2 |
.70 |
| 5218 |
12.8 |
.25 |
| 5566 |
11.1 |
.20 |
| 7723 |
11.8 |
+0.18 |
| Mean |
11.48 |
+0.317 |
| SBc (15) |
| 613 |
10.6 |
+0.60 |
| 779 |
12.1 |
.48 |
| 3206 |
13.3 |
.45 |
| 3344 |
11.4 |
.60 |
| 3346 |
12.3 |
.40 |
| 3625 |
13.3 |
.0 |
| 3686 |
12.0 |
.30 |
| 3769 |
12.8 |
.43 |
| 3953 |
11.1 |
.74 |
| 3992 |
11.5 |
.85 |
| 4303* |
10.6 |
.78 |
| 4579* |
9.7 |
.45 |
| 5383 |
12.6 |
.40 |
| 5921 |
12.8 |
.70 |
| 7479 |
12.1 |
+0.48 |
| Mean |
11.87 |
+0.509 |
| Peculiar (2) |
| 2782 |
12.3 |
+0.26 |
| 4314 |
11.1 |
+0.34 |
{14}
TABLE III
Normal Spirals
| N.G.C. |
mT |
log d |
| Sa (49) |
| 488 |
11.8 |
+0.48 |
| 676 |
13.3 |
.30 |
| 1332 |
10.9 |
.43 |
| 2655 |
11.1 |
.60 |
| 2681 |
10.7 |
.48 |
| 2775 |
10.9 |
.32 |
| 2811 |
12.3 |
.28 |
| 2855 |
12.8 |
.11 |
| 3169§ |
12.3 |
.60 |
| 3245 |
11.8 |
.30 |
| 3301 |
12.4 |
.15 |
| 3368* |
10.0 |
.85 |
| 3516 |
12.1 |
.20 |
| 3619 |
12.3 |
.0 |
| 3626* |
11.3 |
.28 |
| 3665 |
12.0 |
.0 |
| 3682 |
12.1 |
.08 |
| 3898 |
12.0 |
.43 |
| 3941 |
10.3 |
.30 |
| 4036 |
10.9 |
.60 |
| 4138 |
12.1 |
.20 |
| 4143 |
11.3 |
.11 |
| 4150 |
12.0 |
.11 |
| 4251 |
10.4 |
.26 |
| 4268 |
12.8 |
.0 |
| 4274 |
11.1 |
+0.54 |
| 4281 |
11.5 |
+0.18 |
| 4429 |
11.5 |
.48 |
| 4452 |
12.6 |
.15 |
| 4526 |
11.1 |
.70 |
| 4550 |
12.1 |
.43 |
| 4570 |
11.1 |
.38 |
| 4594 |
9.1 |
.85 |
| 4665 |
11.8 |
+ .08 |
| 4684 |
12.2 |
– .22 |
| 4698 |
11.9 |
+ .43 |
| 4710 |
11.8 |
.54 |
| 4762 |
11.5 |
.57 |
| 4866 |
12.0 |
.50 |
| 4958 |
11.4 |
.60 |
| 5377 |
11.8 |
.48 |
| 5389 |
12.5 |
.25 |
| 5422 |
12.1 |
+ .40 |
| 5631 |
12.0 |
– .05 |
| 5866* |
11.7 |
+ .48 |
| 7013 |
12.8 |
.08 |
| 7457 |
12.8 |
.30 |
| 7727 |
11.3 |
.43 |
| 7814* |
11.4 |
+0.48 |
| Mean |
11.69 |
+0.333 |
| Sb (70) |
| 224 |
5.0 |
+2.25 |
| 672 |
12.8 |
0.54 |
| 772 |
11.1 |
.70 |
| 949 |
13.3 |
.0 |
| 955 |
12.9 |
.40 |
| 1068 |
9.1 |
.40 |
| 1309 |
12.0 |
.15 |
| 2639 |
12.2 |
.0 |
| 2715 |
12.5 |
.40 |
| 2748 |
12.0 |
.32 |
| 2841* |
9.4 |
.78 |
| 2985 |
11.4 |
0.48 |
| 3031* |
8.3 |
+1.20 |
| 3182 |
12.9 |
–0.22 |
| 3190 |
11.9 |
+ .48 |
| 3227 |
12.0 |
.48 |
| 3277 |
12.6 |
.0 |
| 3310 |
10.4 |
+ .18 |
| 3380 |
12.1 |
– .05 |
| 3489* |
11.2 |
+0.40 |
| 3556 |
11.1 |
+0.90 |
| 3593 |
11.9 |
.60 |
| 3623* |
9.9 |
.90 |
| 3627* |
9.1 |
0.90 |
| 3628§ |
11.4 |
+1.08 |
| 3632 |
13.3 |
–0.10 |
| 3675 |
11.4 |
+ .48 |
| 3681 |
13.0 |
.0 |
| 3684 |
13.0 |
+ .08 |
| 3895 |
13.3 |
– .05 |
| 3900 |
12.1 |
+ .25 |
| 3938 |
12.1 |
.65 |
| 4020 |
12.3 |
.17 |
| 4030 |
11.1 |
.30 |
| 4051* |
11.9 |
.60 |
| 4085 |
12.5 |
.36 |
| 4151 |
12.0 |
.40 |
| 4192 |
10.9 |
.90 |
| 4216* |
10.8 |
0.85 |
| 4244§ |
12.3 |
+1.11{15} |
| 4258* |
8.7 |
+1.30 |
| 4273 |
11.8 |
0.20 |
| 4438* |
10.3 |
.54 |
| 4448 |
11.8 |
.48 |
| 4450 |
10.6 |
+ .57 |
| 4451 |
12.8 |
– .15 |
| 4500 |
12.8 |
+0.17 |
| 4565*§ |
11.0 |
1.17 |
| 4736* |
8.4 |
0.70 |
| 4750 |
11.8 |
.26 |
| 4800 |
11.8 |
.04 |
| 4814 |
12.7 |
.56 |
| 4826 |
9.0 |
.90 |
| 5055* |
9.6 |
.90 |
| 5376 |
12.8 |
+ .17 |
| 5379 |
12.9 |
–0.05 |
| 5394 |
13.3 |
+0.17 |
| 5633 |
13.0 |
– .10 |
| 5713 |
12.3 |
+ .32 |
| 5740 |
12.3 |
.48 |
| 5746 |
10.4 |
.87 |
| 5750 |
12.8 |
.15 |
| 5772 |
12.0 |
.25 |
| 5806 |
12.3 |
.30 |
| 5985 |
12.0 |
.60 |
| 6207 |
11.8 |
.30 |
| 6643 |
11.9 |
.48 |
| 7331* |
10.4 |
.95 |
| 7541 |
12.7 |
.41 |
| 7606 |
12.0 |
+0.78 |
| Mean |
11.55 |
+0.471 |
| Sc (115) |
| 157 |
11.4 |
+0.40 |
| 253 |
9.3 |
1.34 |
| 278 |
12.0 |
0.08 |
| 470 |
13.1 |
0.20 |
| 598 |
7.0 |
1.78 |
| 615 |
12.3 |
0.43 |
| 628* |
10.6 |
.90 |
| 908 |
11.9 |
.60 |
| 1084 |
11.4 |
.34 |
| 1087 |
12.1 |
.36 |
| 1637 |
12.6 |
.48 |
| 2339 |
13.1 |
0.28 |
| 2403* |
8.7 |
1.20 |
| 2532 |
13.3 |
0.17 |
| 2683 |
9.9 |
1.00 |
| 2712 |
12.3 |
0.20 |
| 2742 |
11.8 |
.40 |
| 2776 |
12.3 |
0.34 |
| 2903* |
9.1 |
1.04 |
| 2964 |
11.6 |
.40 |
| 2976 |
12.0 |
.50 |
| 3003§ |
13.3 |
.78 |
| 3021 |
12.3 |
.11 |
| 3079§ |
12.0 |
.90 |
| 3147 |
11.4 |
.30 |
| 3166 |
12.0 |
.0 |
| 3184 |
12.7 |
.78 |
| 3198 |
13.0 |
.95 |
| 3254 |
12.8 |
.60 |
| 3294 |
12.0 |
.48 |
| 3389 |
13.1 |
+0.30 |
| 3395 |
12.6 |
+0.11 |
| 3396 |
13.3 |
– .10 |
| 3430 |
12.6 |
+ .49 |
| 3432 |
12.0 |
.79 |
| 3437 |
12.4 |
.28 |
| 3445 |
13.1 |
.08 |
| 3448 |
12.3 |
.26 |
| 3486 |
11.8 |
.58 |
| 3488 |
12.8 |
.25 |
| 3512 |
12.3 |
.0 |
| 3521* |
10.1 |
.65 |
| 3549 |
13.3 |
.43 |
| 3596 |
13.3 |
.60 |
| 3631 |
11.8 |
.66 |
| 3642 |
12.0 |
.73 |
| 3655 |
11.9 |
.04 |
| 3666 |
11.8 |
.54 |
| 3672 |
13.0 |
.54 |
| 3683 |
12.0 |
.15 |
| 3780 |
13.0 |
.40 |
| 3810 |
11.3 |
.62 |
| 3813 |
12.3 |
.32 |
| 3877 |
11.8 |
.64 |
| 3887 |
12.3 |
.40 |
| 3893 |
11.8 |
.61 |
| 3949 |
11.8 |
.34 |
| 3982 |
12.1 |
.36 |
| 4013 |
13.3 |
.60 |
| 4041 |
11.4 |
.30 |
| 4062 |
12.6 |
.48 |
| 4088 |
11.5 |
.+0.72{16} |
| 4096 |
12.3 |
+0.78 |
| 4100 |
12.3 |
.60 |
| 4145 |
12.3 |
.70 |
| 4157§ |
12.3 |
.77 |
| 4212 |
12.3 |
.30 |
| 4220 |
12.1 |
0.40 |
| 4236 |
12.8 |
1.04 |
| 4254 |
10.4 |
0.65 |
| 4321* |
10.5 |
.70 |
| 4414 |
10.1 |
.48 |
| 4419 |
11.8 |
.36 |
| 4460 |
12.1 |
.20 |
| 4490* |
10.2 |
.60 |
| 4501* |
10.5 |
.70 |
| 4504 |
12.1 |
0.48 |
| 4517§ |
12.5 |
1.00 |
| 4536§ |
12.3 |
0.85 |
| 4559 |
10.7 |
.90 |
| 4569* |
10.9 |
.65 |
| 4580 |
12.3 |
.15 |
| 4605 |
9.9 |
0.48 |
| 4631* |
9.5 |
1.08 |
| 4632 |
13.1 |
0.50 |
| 4666 |
12.0 |
.60 |
| 4713 |
12.3 |
.38 |
| 4781 |
11.8 |
.48 |
| 4793 |
12.4 |
.20 |
| 4808 |
12.6 |
+0.34 |
| 4995 |
11.8 |
+0.36 |
| 5005* |
11.1 |
.70 |
| 5012 |
11.9 |
.43 |
| 5033* |
11.8 |
0.78 |
| 5194* |
7.4 |
1.08 |
| 5204 |
12.8 |
0.59 |
| 5236 |
10.4 |
1.00 |
| 5247 |
13.3 |
0.70 |
| 5248 |
11.5 |
.50 |
| 5290 |
12.5 |
.48 |
| 5297 |
12.6 |
.60 |
| 5364 |
13.3 |
.60 |
| 5395 |
12.8 |
0.30 |
| 5457 |
9.9 |
1.34 |
| 5474 |
12.0 |
0.60 |
| 5585 |
12.3 |
.60 |
| 5676 |
11.8 |
.48 |
| 5678 |
11.8 |
.41 |
| 5832 |
13.1 |
0.56 |
| 5907§ |
11.9 |
1.04 |
| 6181 |
12.5 |
0.30 |
| 6217 |
12.1 |
.25 |
| 6503 |
9.9 |
.70 |
| 7448 |
11.8 |
+ .30 |
| 7671 |
13.3 |
– .15 |
| Mean |
11.75 |
+0.537 |
| Peculiar Spirals (Unclassified) |
| 972 |
13.3 |
+0.17 |
| 2537 |
13.3 |
.0 |
| 4900 |
11.8 |
+0.23 |
RELATION BETWEEN LUMINOSITIES AND DIAMETERS
Among the nebulae of each separate type are found linear correlations
between total magnitudes and logarithms of diameters. These are
shown in Figures 2–5 for the beginning, middle, and end of the sequence
of types and also for the irregular nebulae. In Figures 2 and 3
adjacent types have been grouped in order to increase the material, and
in Figure 5 the Magellanic Clouds have been added to increase the range.
The correlations can be expressed in the form
where K is constant from type to type, but C varies progressively
throughout the sequence. The value of K cannot be accurately
determined{17} from the scattered data for any particular type, but,
within the limits of uncertainty, it approximates the round number 5.0,
the value which is represented by the lines in Figures 2–5.
When K is known, the value of C can be computed from the mean magnitude
and the logarithm of the diameter for each type. This amounts to
reading from the curves the magnitudes corresponding to a diameter
of one minute of arc, but avoids the uncertainty of establishing the
curves where the data are limited.
TABLE IV
Irregular Nebulae
| N.G.C. |
mT |
log d |
| 2968 |
12.6 |
+0.08 |
| 3034* |
9.0 |
.85 |
| 3077 |
11.4 |
.48 |
| 3729 |
11.8 |
.17 |
| 4214* |
11.3 |
.90 |
| 4449* |
9.5 |
.65 |
| 4618 |
12.3 |
+0.40 |
| 4656§ |
11.5 |
+1.30 |
| 4753 |
11.4 |
+0.43 |
| 5144 |
12.8 |
– .30 |
| 5363 |
11.1 |
+0.20 |
| Mean |
11.34 |
+0.469 |
NOTES TO TABLES I–IV
* Magnitude from Hopmann.
† N.G.C. 524 and 3998 are late elliptical nebulae in which the
equatorial planes are perpendicular to the line of sight. They might be
included with the E6 or E7 nebulae.
§ Absorption very conspicuous.
‡ N.G.C. 3607, 4459, and 5485 appear to be elliptical nebulae with
narrow bands of absorption between the nuclei and the peripheries.
The progressive change in the value of C throughout the sequence may be
expressed as a variation either in the magnitude for a given diameter
or in the diameter for a given magnitude. Both effects are listed in
Table VII and are illustrated in Figure 6, in which magnitudes and
diameters thus found are plotted against types. With the exception of
the later elliptical nebulae, for which the data are wholly inadequate
for reliable determinations, the points fall on smooth curves. In the
region of the earlier elliptical nebulae, the curves should be somewhat
steeper in order to allow for objects of greater ellipticities which
are probably included.
REDUCTION OF NEBULAE TO A STANDARD TYPE
The slope, K, in the formula relating magnitudes with diameters,
appears to be closely similar for the various types, but accurate
determinations{18} are restricted by the limited and scattered nature
of the data for each type separately. With a knowledge of the parameter
C, however, it is possible to reduce all the material to a standard{19}
type and hence to determine the value of K from the totality of the
data. The mean of E7, SBa, and Sa was chosen for the purpose, as
representing a hypothetical transition-point between the elliptical
nebulae and the spirals, and was designated by the symbol “S0.”
The corresponding value of C, in round numbers, is 13.0. Corrections
were applied to the logarithms of the diameters of the nebulae of each
observed class, amounting to
 where C is the observed value for a particular class.17 When
the values of C are read from the smooth curve in Figure 6, these
corrections are as shown in Table VIII.
where C is the observed value for a particular class.17 When
the values of C are read from the smooth curve in Figure 6, these
corrections are as shown in Table VIII.
TABLE V
Frequency Distribution of Types
| Type |
Number |
Percentage |
Mean Mag. |
| Elliptical Nebulae |
| E0 |
17 |
18 |
11.40 |
| 1 |
13 |
14 |
11.43 |
| 2 |
14 |
15 |
11.52 |
| 3 |
10 |
11 |
11.99 |
| 4 |
13 |
14 |
11.95 |
| 5 |
6 |
6 |
10.97 |
| 6 |
7 |
8 |
10.93 |
| 7 |
5 |
5 |
11.02 |
| Pec |
8 |
9 |
11.55 |
| Total |
93 |
23* |
11.53 |
| Normal Spirals |
| Sa |
49 |
21 |
11.69 |
| b |
70 |
29 |
11.55 |
| c |
115 |
49 |
11.75 |
| Pec |
3 |
1 |
12.80 |
| Total |
237 |
59* |
11.68 |
| Barred Spirals |
| SBa |
26 |
44 |
11.66 |
| b |
16 |
27 |
11.48 |
| c |
15 |
26 |
11.87 |
| Pec |
2 |
3 |
11.70 |
| Total |
59 |
15* |
11.66 |
| Irregular Nebulae |
|
11 |
3* |
11.34 |
| Totals |
| All types |
400 |
100 |
11.63 |
* Percentages of 400, the total number of nebulae investigated. The
percentages of the subtypes refer to the number of nebulae in the
particular type.
TABLE VI
Frequency Distribution of Magnitudes
| Magnitude Interval |
Numbers of Nebulae |
| E |
S |
All |
| 8.1– 8.5 |
0 |
2 |
2 |
| 8.6– 9.0 |
2 |
4 |
7 |
| 9.1– 9.5 |
4 |
6 |
11 |
| 9.6–10.0 |
7 |
7 |
19 |
| 10.1–10.5 |
7 |
13 |
20 |
| 10.6–11.0 |
8 |
14 |
32 |
| 11.1–11.5 |
9 |
24 |
49 |
| 11.6–12.0 |
21 |
57 |
88 |
| 12.1–12.5 |
20 |
52 |
86 |
| 12.6–13.0 |
10 |
33 |
51 |
The corrected values of log d were then plotted against the observed
magnitudes. This amounts to shifting the approximately parallel
correlation curves for the separate types along the axis of log d
until they coincide. Since the mean magnitudes of the various types
are nearly constant, the relative shifts will very nearly equal the
differences in the mean observed log d, and hence the effect of errors
in the first approximation to the values of K will be negligible.
{20}

Fig. 1.—Frequency distribution of apparent magnitudes
among nebulae in Holetschek’s list.

Fig. 2.—Relation between luminosity and diameter among
nebulae at the beginning of the sequence of types—E0 and E1 nebulae.
The plot is shown in Figure 7, in which the two Magellanic{21} Clouds
have been included in order to strengthen the bright end of the curve
which would otherwise be unduly influenced by the single{22} object, M
31. The magnitudes +0.5 and +1.5, which were assigned to the Clouds,
are estimates based upon published descriptions.

Fig. 3.—Relation between luminosity and diameter among
nebulae at the middle of the sequence of types—E7, Sa, and SBa nebulae.

Fig. 4.—Relation between luminosity and diameter among
nebulae at the end of the sequence of types—Sc and SBc nebulae.
The correlation of the data is very closely represented by the formula
This falls between the two regression curves derived from least-square
solutions and could be obtained exactly by assigning appropriate
weights to the two methods of grouping. The nature of the data is such
that a closer agreement can scarcely be expected. No correction to the
assumed value of the slope appears to be required. The material extends
over a range of 12 mag., and the few cases which have been investigated
indicate that the correlation can be extended another 3 mag., to the
limit at which nebulae can be classified with certainty on photographs
made with the 100-inch reflector. The relation may therefore be
considered to hold throughout the entire range of observations.

Fig. 5.—Relation between luminosity and diameter among
the irregular nebulae. The Magellanic Clouds are included. N.G.C. 4656
is an exceptional case in that it shows a narrow, greatly elongated
image in which absorption effects are very conspicuous; hence the
maximum diameter is exceptionally large for its apparent luminosity.
{23}
The residuals without regard to sign average 0.87 mag., and there
appears to be no systematic effect due either to type or luminosity.
The scatter, however, is much greater for the spirals, especially in
the later types, than for the elliptical nebulae. The limiting cases
are explained by peculiar structural features. The nebulae which fall
well above the line usually have bright stellar nuclei, and those which
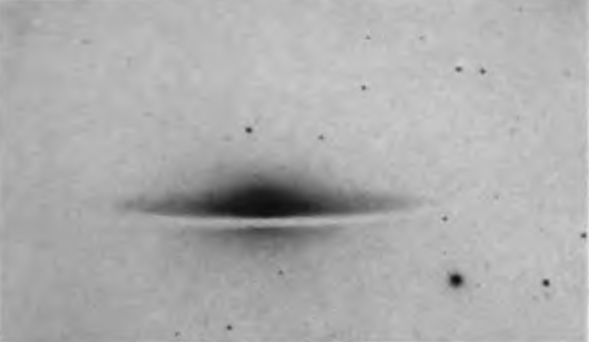
fall lowest are spirals seen edge-on in which belts of absorption are
conspicuous.
TABLE VII
| Type |
mT |
log d |
C* |
d† |
| E0 |
11.40 |
–0.204 |
10.38 |
1.2 |
| 1 |
11.43 |
.177 |
10.54 |
1.3 |
| 2 |
11.52 |
.088 |
11.08 |
1.6 |
| 3 |
11.99 |
.133 |
11.33 |
1.8 |
| 4 |
11.95 |
– .011 |
11.90 |
2.4 |
| 5 |
10.97 |
+ .090 |
11.42 |
1.9 |
| 6 |
10.93 |
.220 |
12.03 |
2.5 |
| 7 |
11.02 |
.360 |
12.82 |
3.7 |
| Sa |
11.69 |
.333 |
13.35 |
4.7 |
| b |
11.55 |
.471 |
13.90 |
6.0 |
| c |
11.74 |
.540 |
14.44 |
7.7 |
| SBa |
11.66 |
.267 |
13.00 |
4.0 |
| b |
11.48 |
.317 |
13.16 |
4.3 |
| c |
11.87 |
.509 |
14.41 |
7.6 |
| Irr |
11.34 |
+0.469 |
13.68 |
5.4 |
* C = mT + 5 log d.
† log d = 0.2 (C — mT); mT = 10.0.
EFFECTS OF ORIENTATION
The effect of the orientation is appreciable among the spirals in
general. In order to illustrate this feature, they have been divided
into three groups consisting of those whose images are round or nearly
round, elliptical, and edge-on, or nearly so. The mean values of mT
+ 5 log d were then computed and compared with the theoretical value,
13.0. The residuals are negative when the nebulae are too bright for
their diameters and positive when they are too faint. The results are
given in Table IX, where mean residuals are followed by the numbers of
nebulae, in parentheses, which are represented by the means.
{24}
The numbers of the barred spirals are too limited to inspire confidence
in the results, but among the normal spirals there is conclusive
evidence that the highly tilted and edge-on nebulae are fainter for a
given diameter than those seen in the round. A study of the individual
images indicates that the effect is due very largely to dark absorption
clouds, which become more conspicuous when the nebulae are highly
tilted. These clouds are generally, but not universally, peripheral
features. An extensive investigation will be necessary before any
residual effect due to absorption by luminous nebulosity can be
established with certainty. Even should such exist, it clearly cannot
be excessive.
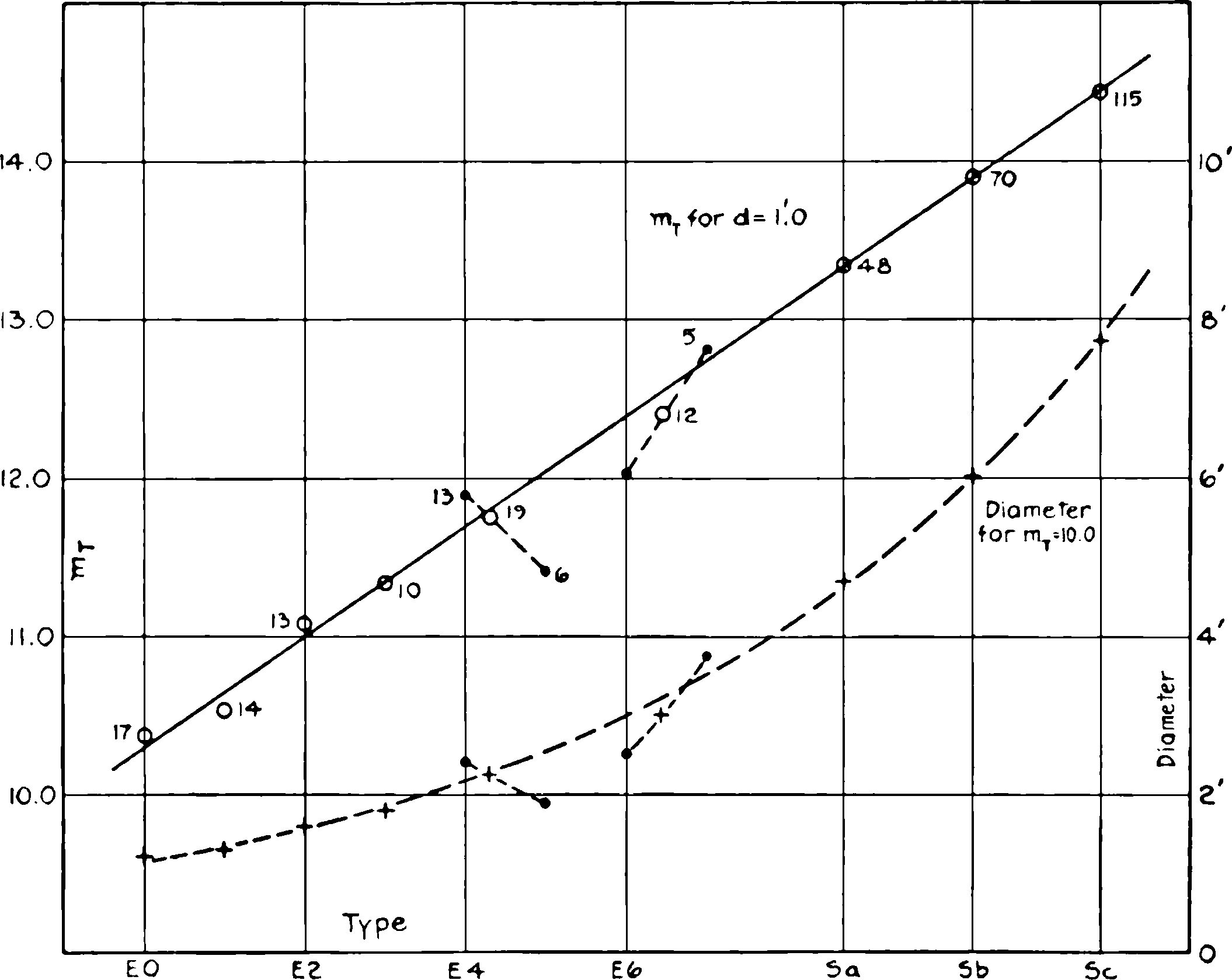
Fig. 6.—Progressive characteristics in the sequence of
types. The upper curve represents the progression in total magnitude
with type for nebulae having maximum diameters of one minute of
arc. The elliptical nebulae and the normal spirals are included as
representing the normal sequence, but the barred spirals and the
irregular nebulae are omitted. The figures give the number of objects
observed in each type. Among the later elliptical nebulae the numbers
are so small that means of adjacent types have been plotted. The lower
curve represents the progression in diameter along the normal sequence
for nebulae of the tenth magnitude.
TABLE VIII
| Type |
C |
Δ log d |
| E0 |
10.30 |
+0.54 |
| 1 |
10.65 |
.47 |
| 2 |
11.00 |
.40 |
| 3 |
11.35 |
.33 |
| 4 |
11.70 |
.26 |
| 5 |
12.05 |
.19 |
| 6 |
12.40 |
.12 |
| 7 |
12.75 |
+0.05 |
| Sa |
13.31 |
–0.06 |
| Sb |
13.90 |
.18 |
| Sc |
14.45 |
.29 |
| SBa |
13.00 |
.00 |
| SBb |
13.16 |
.03 |
| SBc |
14.41 |
.28 |
| Irr |
13.68 |
–0.14 |

Fig. 7.—Relation between luminosity and diameter among
extra-galactic nebulae. The nebulae have been reduced to a standard
type, S0, which, being the mean of E7, Sa, and SBa, represents a
hypothetical transition point between elliptical nebulae and spirals.
The Magellanic Clouds have been included in order to strengthen the
brighter end of the plot.
SIGNIFICANCE OF THE LUMINOSITY RELATION
The correlations thus far derived are between total luminosities and
maximum diameters. In the most general sense, therefore, they{25}
express laws of mean surface brightness. The value, K = 5.0, in formula
(1) indicates that the surface brightness is constant for each separate
type. The variations in C indicate a progressive diminution in the
surface brightness from class to class throughout the entire sequence.
The consistency of the results amply justifies the sequence as a basis
of classification, since a progression in physical dimensions{26}
is indicated, which accompanies the progression in structural form.
Although the correlations do not necessarily establish any generic
relation among the observed classes, they support in a very evident
manner the hypothesis that the various stages in the sequence represent
different phases of a single fundamental type of astronomical body.
Moreover, the quantitative variation in C is consistent with this
interpretation, as is apparent from the following considerations.
TABLE IX
Residuals in mT + 5 log d as a Function of Orientation
| Type |
Round |
Elliptical |
Edge-On |
| Sa |
|
–0.02 (13) |
–0.27 (13) |
+0.57 (23) |
| Sb |
|
.77 (24) |
.0 (35) |
1.71 (11) |
| Sc |
|
–0.08 (35) |
–0.13 (57) |
+0.66 (22) |
|
All S |
–0.26 (72) |
–0.11 (105) |
+0.83 (56) |
| SBa |
|
0.0 (10) |
–0.30 (7) |
+0.31 (8) |
| SBb |
|
– .16 (10) |
+ .07 (6) |
|
| SBc |
|
+0.19 (9) |
–0.50 (4) |
+0.32 (2) |
|
All SB |
+0.01 (29) |
+0.21 (17) |
+0.31 (10) |
|
All spirals |
–0.22 (101) |
–0.13 (122) |
+0.73 (66) |
Among the elliptical nebulae it is observed that the nuclei are sharp
and distinct and that the color distribution is uniform over the
images. This indicates that there is no appreciable absorption, either
general or selective, and hence that the luminosity of the projected
image represents the total luminosity of the nebula, regardless of
the orientation. If the observed classes were pure, that is, if the
apparent ellipticities were the actual ellipticities, formula (1) could
be written
where b is the minor diameter in minutes of arc and e is the
ellipticity. The term mT + 5 log b is observed to be constant for a
given type. If it were constant for all elliptical nebulae, then the
term Ce + 5 log (1 – e) would be constant also. On this assumption,
{27}
where C0 is the value of C for the pure class E0. Hence
a relation which can be tested by the observations. An analysis of the
material indicates that this is actually the case, and hence that among
the elliptical nebulae in general, the minor diameter determines the
total luminosity, at least to a first approximation.18
The observed values of C vary with the class, as is seen in Table VII
and Figure 6, but, excepting that for E7, they are too large because of
the mixture of later types of nebulae among those of a given observed
class. It is possible, however, to calculate the values of Ce –
C0 for the pure classes and then to make approximate corrections
for the observed mixtures on the assumption that the nebulae of any
given actual ellipticity are oriented at random. In this manner, mean
theoretical values can be compared with the observed values. The
comparisons are shown in Table XII in the form C7 – Ce, because
E7 is the only observed class that can be considered as pure. The
significance of the table will be discussed later.
The following method has been used to determine the relative
frequencies with which nebulae of a given actual ellipticity, oriented
at random, will be observed as having various apparent ellipticities.
In Figure 8, let the co-ordinate axes OX and OY coincide with the
major and minor axes, a and b, of a meridian section of an ellipsoid
of revolution. Let OO′ be the line of sight to the observer, making an
angle i with OX, and let OR be perpendicular to OO′. Let PP′ be a{28}
tangent to the ellipse, parallel to and at a distance from OO′. Let
x0 and y0 be the intercepts of the tangent on the X- and Y-axis,
respectively. The apparent ellipticity is determined by bx, which,
for various values of the angle i, ranges from b to a. The problem is
to determine the relative areas on the surface of a sphere whose center
is O, within which the radius OY must pass in order that the values of
b1, and hence of the apparent ellipticity, e1 may fall within
certain designated limits. This requires that the angle i be expressed
in terms of b1.
From the equation of the tangent, PP′,

 Since
Since

 Let a = 1, then
Let a = 1, then
 where
where

From these equations, the values of i can be determined for all
possible values of e1. The limits for the observed classes E0 to E7
were chosen midway between the consecutive tenths, E0 ranging{29} from
e = 0 to e = 0.05; E1, from e = 0.05 to e = 0.15; E7, from e = 0.65
to e = 0.75. The relative frequencies of the various observed classes
are then proportional to the differences in sin i corresponding to the
two limiting values of e1. These frequencies must be calculated
separately for nebulae of different actual ellipticities.
The results are given in Table X, where the actual ellipticities,
listed in the first column, are followed across the table by the
percentages which, on the assumption of random orientation, will be
observed as having the various apparent ellipticities. The bottom
row will be seen to show the percentages of apparent ellipticities
observed in an assembly of nebulae in which the numbers for each actual
ellipticity are equal and all are oriented at random.
TABLE X
| Actual |
Apparent |
| E0 |
E1 |
E2 |
E3 |
E4 |
E5 |
E6 |
E7 |
Total |
| E7 |
0.055 |
0.111 |
0.114 |
0.116 |
0.121 |
0.132 |
0.164 |
0.187 |
1.000 |
| 6 |
.059 |
.123 |
.126 |
.133 |
.148 |
.187 |
0.224 |
|
|
| 5 |
.067 |
.140 |
.148 |
.166 |
.216 |
0.263 |
|
|
|
| 4 |
.079 |
.169 |
.190 |
.250 |
0.312 |
|
|
|
|
| 3 |
.100 |
.225 |
.299 |
0.376 |
|
|
|
|
|
| 2 |
.145 |
.378 |
0.477 |
|
|
|
|
|
|
| 1 |
0.300 |
0.700 |
|
|
|
|
|
|
|
| 0 |
1.000 |
|
|
|
|
|
|
|
|
| Total |
1.805 |
1.846 |
1.354 |
1.041 |
0.797 |
0.582 |
0.388 |
0.187 |
8.000 |
| 0.226 |
0.231 |
0.169 |
0.130 |
0.100 |
0.073 |
0.049 |
0.023 |
1.000 |
From this table and the actual numbers in the observed classes as
read from a smoothed curve, the numbers of each actual ellipticity
mingled in the observed classes can be determined. For instance, the
four nebulae observed as E7 represent 0.187 of the total number of
actual E7. The others are distributed among the observed classes E0
to E6 according to the percentages listed in Table X. Six nebulae are
observed as E6, but 3.6 of these are actually E7. The remaining 2.4
actual E6 nebulae represent 0.224 of the total number of that actual
ellipticity, the others, as before, being scattered among the observed
classes E0 to E5. Table XI gives the complete analysis and is similar
to Table X except that the percentages in the latter are replaced by
the actual numbers indicated by the observations.
{30}
Finally, the mean values of C7 – Ce are calculated from the
numbers of nebulae in the various columns of Table XI together with
the values of C7 – Ce for the pure classes as derived from
formula (4). The results are listed in the fourth column of Table XII
following those for the pure and the observed classes. In determining
the observed values, N.G.C. 524 and 3998 are included as E0 and E1,
although in Table I they are listed as peculiar, because they are
obviously much flattened nebulae whose minor axes are close to the line
of sight.
TABLE XI
| Actual |
Apparent |
| E0 |
E1 |
E2 |
E3 |
E4 |
E5 |
E6 |
E7 |
Total |
| E7 |
1.2 |
2.4 |
2.5 |
2.5 |
2.6 |
2.9 |
3.6 |
4.0 |
21.7 |
| 6 |
0.6 |
1.3 |
1.4 |
1.5 |
1.6 |
2.0 |
2.4 |
|
10.8 |
| 5 |
.8 |
1.7 |
1.8 |
2.0 |
2.7 |
3.1 |
|
|
12.1 |
| 4 |
.8 |
1.7 |
1.9 |
2.5 |
3.1 |
|
|
|
10.0 |
| 3 |
.9 |
2.1 |
2.8 |
3.5 |
|
|
|
|
9.3 |
| 2 |
1.1 |
2.9 |
3.6 |
|
|
|
|
|
7.6 |
| 1 |
1.7 |
3.9 |
|
|
|
|
|
|
5.6 |
| 0 |
9.9 |
|
|
|
|
|
|
|
9.9 |
| Total* |
17.0 |
16.0 |
14.0 |
12.0 |
10.0 |
8.0 |
6.0 |
4.0 |
87.0 |
* The totals represent the numbers in the observed classes as read from
a smooth curve.
The observed values in general fall between those for the pure
classes and those corresponding to random orientation. They are of
the same order as the latter, and the discrepancies are perhaps not
unaccountably large in view of the nature and the limited extent of the
material. There is a systematic difference, however, averaging about
0.2 mag., in the sense that the observed values are too large, and
increasing with decreasing ellipticity. One explanation is that the
observed classes are purer than is expected on the assumption of random
orientation. This view is supported by the relatively small dispersion
in C, as may be seen in Table I and Figure 2, among the nebulae of a
given class, but it is difficult to account for any such selective
effect in the observations. The discrepancies may be largely eliminated
by an arbitrary adjustment of the numbers of nebulae with various
degrees of actual ellipticity; for instance, the values in{31} the last
column of Table XII, calculated on the assumption of equal numbers,
agree very well with the observed values, although the resulting
numbers having the various apparent ellipticities differ slightly from
those observed. The observed values, however, can again be accounted
for by the inclusion of some flatter nebulae among the classes E6 and
E7. Very early Sa or SBa nebulae might easily be mistaken for E nebulae
when oriented edge-on, although they would be readily recognized when
even slightly tilted. If the numerical results fully represented actual
statistical laws, the explanation would be sought in the physical
nature of the nebulae. The change from ellipsoidal to lenticular
figures, noticeable in the later-type nebulae, would affect the results
in the proper direction, as would also a progressive shortening of the
polar axis. The discrepancies, however, are second-order effects, and
since they may be due to accidental variations from random orientation,
a further discussion must await the accumulation of more data.
TABLE XII
Differential Values of C
| Class |
Pure Classes |
Observed |
Random Orientation |
| No. as Observed |
Equal No. |
| C7–C7 |
0.00 |
0.00 |
0.00 |
0.00 |
| C6 |
0.63 |
0.35* |
0.25 |
0.35 |
| C5 |
1.10 |
0.70* |
0.58 |
0.70 |
| C4 |
1.51 |
0.85 |
1.11 |
1.01 |
| C3 |
1.84 |
1.42 |
0.87 |
1.28 |
| C2 |
2.13 |
1.67 |
1.33 |
1.55 |
| C1 |
2.39 |
2.01† |
1.54 |
1.83 |
| C0 |
2.62 |
2.17† |
2.15 |
2.25 |
* Read from smooth curve in Fig. 6. The small numbers of observed E5
and E6 nebulae justify this procedure. The other values are the means
actually observed.
† N.G.C. 524 and 3998 are included as E0 and E1, respectively.
Meanwhile, it is evident that, to a first approximation at least,
the polar diameters alone determine the total luminosities of all
elliptical nebulae, and the entire series can be represented by the
various configurations of an originally globular mass expanding
equatorially. A single formula represents the relation, in which the
value of C is that corresponding to the pure type E0. From Table XII,{32}
this is found to be 2.62 mag. less than the value of C7 The
latter is observed to be 12.75, hence
If this relation held for the spirals as well, the polar diameters
could be calculated from the measured magnitudes. Unfortunately, it has
not been possible to measure accurately the polar diameters directly,
and hence to test the question, but they have been computed for the
mean magnitudes of the Sa, Sb, and Sc nebulae as given in Table III,
and the ratios of the axes have been derived by a comparison of these
hypothetical values with the means of the measured maximum diameters.
The results, 1 to 4.4, 1 to 5.7, and 1 to 7.3, respectively, although
of the right order, appear to be somewhat too high. An examination of
the photographs indicates values of the order of 1 to 5.5, 1 to 8, and
1 to 10, but the material is meager and may not be representative. The
comparison emphasizes, however, the homogeneity and the progressive
nature of the entire sequence of nebulae and lends some additional
color to the assumption that it represents various aspects of the same
fundamental type of system.
From the dynamical point of view, the empirical results are consistent
with the general order of events in Jeans’s theory. Thus interpreted,
the series is one of expansion, and the scale of types becomes the
time scale in the evolutionary history of nebulae. In two respects
this scale is not entirely arbitrary. Among the elliptical nebulae the
successive types differ by equal increments in the ellipticity or the
degree of flattening, and among the spirals the intermediate stage is
midway between the two end-stages in the structural features as well as
in the luminosity relations.
One other feature of the curves may be discussed from the point of view
of Jeans’s theory before returning to the strictly empirical attitude.
The close agreement of the diameters for the stages E7 and Sa suggests
that the transition from the lenticular nebula to the normal spiral
form is not cataclysmic. If the transition were gradual, however, we
should expect to observe occasional objects in the very process, but
among the thousand or so nebulae whose images have been inspected, not
one clear case of a transition form has been detected. The observations
jump suddenly from lenticular nebulae{33} with no trace of structure to
spirals in which the arms are fully developed.
If the numerical data could be fully trusted, the SBa forms would fill
the gap. Among these nebulae, the transition from the lenticular to the
spiral with arms is gradual and complete. It is tempting to suppose
that the barred spirals do not form an independent series parallel with
that of the normal spirals, but that all or most spirals begin life
with the bar, although only a few maintain it conspicuously throughout
their history. This would also account for the fact that the relative
numbers of the SBa nebulae are intermediate to those of the lenticular
and of the Sa. The normal spirals become more numerous as the sequence
progresses, while the numbers of barred spirals, on the contrary,
actually decrease with advancing type.
RELATION BETWEEN NUCLEAR LUMINOSITIES AND DIAMETERS
Visual magnitudes have been determined by Hopmann for the
nuclei of 37 of the nebulae included in the present discussion. These
data, together with types and diameters of the nebulae, are listed
in Table XIII. When the magnitudes are plotted directly against
the logarithms of the diameters, they show little or no correlation.
When, however, the nebulae are reduced to the standard type (by
applying corrections for differences in diameter along the sequence),
a decided correlation is found whose coefficient is 0.76. This is
shown in Figure 9 The simple mean of the two regression curves
is
where the slope differs by about 1 per cent from that in formula (2).
The list contains 16 elliptical nebulae, 15 normal, and 6 barred
spirals. The nebulae are fairly representative, except that few
late-type spirals are included. This is an effect of selection due to
the fact that nuclei become less and less conspicuous as the sequence
progresses.
The same result can be derived from a study of the differences, mn – mT,
for the individual nebulae. The mean value is 1.55 ± 0.08, and
the average residual is 0.60 mag. Means for the separate types are to
be found in Table XIV.
TABLE XIII
Diameters and Nuclear Magnitudes
| N.G.C. |
Type |
log d |
mn Hopmann |
mn Reduced |
| 221 |
E2 |
+0.42 |
9.84 |
11.85 |
| 1023 |
SBa |
.78 |
11.86 |
11.86 |
| 2841 |
Sb |
0.78 |
12.08 |
11.19 |
| 3031 |
Sb |
1.20 |
10.94 |
10.05 |
| 3115 |
E7 |
0.60 |
10.83 |
11.09 |
| 3351 |
SBb |
.48 |
12.31 |
12.15 |
| 3368 |
Sa |
.85 |
11.68 |
11.43 |
| 3379 |
E0 |
.30 |
11.55 |
14.27 |
| 3412 |
SBa |
.40 |
11.59 |
11.59 |
| 3489 |
Sb |
.40 |
11.54 |
10.65 |
| 3626 |
Sa |
.28 |
12.37 |
12.12 |
| 3627 |
Sb |
.90 |
12.03 |
11.14 |
| 4125 |
E4 |
.30 |
11.74 |
13.04 |
| 4216 |
Sb |
.85 |
11.65 |
10.76 |
| 4278 |
E1 |
.0 |
12.02 |
14.38 |
| 4374 |
E1 |
.08 |
11.43 |
13.79 |
| 4382 |
E4 |
.48 |
11.77 |
13.07 |
| 4435 |
E6 |
.11 |
11.65 |
12.26 |
| 4438 |
Sb |
.54 |
11.83 |
10.94 |
| 4486 |
E0 |
.30 |
11.23 |
13.95 |
| 4546 |
E6 |
.18 |
11.75 |
12.36 |
| 4552 |
E0 |
.23 |
11.59 |
14.31 |
| 4569 |
Sc |
.65 |
12.05 |
10.57 |
| 4579 |
SBc |
.45 |
11.48 |
10.07 |
| 4621 |
E5 |
.30 |
11.60 |
12.56 |
| 4636 |
E1 |
.08 |
11.97 |
14.33 |
| 4649 |
E2 |
.30 |
11.57 |
13.58 |
| 4697 |
E6 |
.48 |
10.90 |
11.51 |
| 4699 |
SBb |
.57 |
10.72 |
10.56 |
| 4725 |
SBb |
.70 |
11.97 |
11.81 |
| 4736 |
Sb |
.70 |
10.36 |
9.47 |
| 5005 |
Sc |
.70 |
12.04 |
10.56 |
| 5033 |
Sc |
0.78 |
12.38 |
10.90 |
| 5194 |
Sc |
1.08 |
11.38 |
9.90 |
| 5322 |
E3 |
0.15 |
12.10 |
13.76 |
| 5866 |
Sa |
.48 |
11.76 |
11.51 |
| 7331 |
Sb |
+0.95 |
11.82 |
10.93 |
| Means |
|
+0.509 |
11.60 |
11.90 |
The low value for Sa-SBa is due to N.G.C. 5866, for which the{34}
magnitude difference of 0.06 is certainly in error, and the high value
for Sc and SBc, to M 51, for which the difference of 3.98 mag. is not
representative. The latter is accounted for in part by the fact that
the mT refers to the combined magnitude of the main spiral and
the outlying mass, N.G.C. 5195. When these two cases are discarded,
the final mean becomes 1.52 ± 0.05, and the average residual, 0.52
mag., is consistent with the probable errors of the magnitude
determinations.{35} The small numbers of objects within each class are
insufficient for reliable conclusions concerning slight variations
along the sequence. From the constancy of mn – mT, the relation
expressed by formula (6) necessarily follows, the small difference in
the constant being accounted for by the different methods of handling
the data.

Fig. 9.—Relation between nuclear magnitudes and
diameters. The nebulae have been reduced to the standard type by
applying corrections to the magnitudes.
The parallelism of the two curves representing formulae (2) and (6)
indicates that the regular extra-galactic nebulae, when reduced to the
standard type, are similar objects. The mean surface brightness is
constant, and the luminosity of the nucleus, as measured by Hopmann,
is a constant fraction, about one-fourth, of the total luminosity of
the nebulae. If there is a considerable range in absolute magnitude
and hence in actual dimensions, the smaller nebulae must be faithful
miniatures of the larger ones.
ABSOLUTE MAGNITUDES OF EXTRA-GALACTIC NEBULAE
Reliable values of distances, and hence of absolute magnitudes, are
restricted to a very few of the brightest nebulae. These are derived
from a study of individual stars involved in the nebulae, among which
certain types have been identified whose absolute magnitudes in the
galactic system are well known. The method assumes that the{36} stars
involved in the nebulae are directly comparable with the stars in our
own system, and this is supported by the consistency of the results
derived from the several different types which have been identified.
TABLE XIV
| Type |
mn – mT |
Number |
| E0–E3 |
1.64 |
(9) |
|
| E4–E7 |
1.43 |
(7) |
|
| Sa–SBa |
0.97 |
(5) |
1.27 when N.G.C. 5866 is omitted |
| Sb–SBb |
1.70 |
(11) |
|
| Sc–SBc |
1.76 |
(5) |
1.19 when N.G.C. 5194 is omitted |
| Unweighted mean |
1.50 |
(37) |
1.45 (35) |
| Weighted mean |
1.55 |
(37) |
1.52 (35) |
TABLE XV
Absolute Magnitudes of Nebulae
| System |
MT |
MS |
| Galaxy |
|
–5.5 |
| M 31 |
–17.1 |
6.5 |
| LMC |
17.0 |
8.0 |
| SMC |
16.0 |
5.5 |
| M 33 |
15.1 |
6.5 |
| N.G.C. 6822 |
13.7 |
5.8 |
| M 101 |
13.5 |
–6.3 |
| M 32 |
–13.3 |
|
|
|
–6.3 |
|
|
–9.0 = MS – MT |
| Means |
–15.1 |
–15.3 |
| Adopted |
–15.2 |
|
In Table XV are listed absolute magnitudes of the entire system and
of the brightest stars involved, for the galaxy and the seven nebulae
whose distances are known. The data for the Magellanic Clouds are taken
from Shapley’s investigations. The absolute magnitudes of the remaining
nebulae were derived from Holetschek’s apparent magnitudes and the
distances as determined at Mount Wilson, where the stellar magnitudes
were also determined. M 32 is generally assumed to be associated with
the great spiral M 31, because the radial velocities are nearly equal
and are unique in that{37} they are the only large negative velocities
that have been found among the extra-galactic nebulae. M 101 has been
added to the list on rather weak evidence. The brightest stars involved
are slightly brighter than apparent magnitude 17.0, and several
variables have been found with magnitudes at maxima fainter than 19.0.
Sufficient observations have not yet been accumulated to determine
the light-curves of the variables, but from analogy with the other
nebulae they are presumed to be Cepheids. On this assumption, both the
star counts and the variables lead to a distance of the order of 1.7
times the distance of M 33. The inclusion of M 101 does not change the
mean magnitude of the brightest stars involved, but reduces the mean
magnitude of the nebulae by 0.2.
The range in the stars involved is about 2.5 mag., and in the total
luminosities of the nebulae, about 3.8 mag. This latter is consistent
with the scatter in the diagram exhibiting the relation between total
luminosities and diameters. The associated objects, M 31 and 32,
represent the extreme limits among the known systems, and the mean of
these two is very close to the mean of them all.
LUMINOSITY OF STARS INVOLVED IN NEBULAE
The number of nebulae of known distance is too small to serve as a
basis for estimates of the range in absolute magnitude among nebulae in
general. Further information, however, can be derived from a comparison
of total apparent magnitudes with apparent magnitudes of the brightest
stars involved, on the reasonable assumption, supported by such
evidence as is available, that the brightest stars in isolated systems
are of about the same intrinsic luminosity.
The most convenient procedure is to test the constancy of the
differences in apparent magnitude between the brightest stars involved
and the nebulae themselves, over as wide a range as possible in the
latter quantities.
An examination of the photographs in the Mount Wilson collection has
revealed no stars in the very faint objects or in the bright elliptical
nebulae and early-type spirals. This was to be expected from the
conclusions previously derived. Observations were therefore confined to
intermediate- and late-type spirals and the irregular{38} nebulae to
the limiting visual magnitude 10.5. The Magellanic Clouds and N.G.C.
6822 were added to the nebulae in Holetschek’s{39} list. Altogether,
data were available for 32 objects, or about 60 per cent of the total
number in the sky to the adopted limit. For this reason it is believed
that the results are thoroughly representative.
TABLE XVI
Difference in Magnitude between Nebulae and Their Brightest Stars
| N.G.C. |
ms |
mT |
ms – mT |
| Sb |
| 224 |
15.5 |
5.0 |
10.5 |
| 1068 |
17.5 |
9.1 |
8.4 |
| 2841 |
>19.5 |
9.4 |
>10.1 |
| 3031 |
18.5 |
8.3 |
10.2 |
| 3310 |
>19.0 |
10.4 |
> 8.6 |
| 3623 |
>20.0 |
9.9 |
>10.1 |
| 3627 |
18.5 |
9.1 |
9.4 |
| 4438 |
>19.0 |
10.3 |
> 8.7 |
| 4450 |
19.5 |
10.0 |
9.5 |
| 4736 |
17.3 |
8.4 |
8.9 |
| 4826 |
>19.5 |
9.2 |
>10.3 |
| 5055 |
>19.0 |
9.6 |
> 9.4 |
| 5746 |
>19.5 |
10.4 |
> 9.1 |
| 7331 |
19.0 |
10.4 |
8.6 |
| SBb |
| 4699 |
>19.5 |
10.0 |
> 9.5 |
| Sc |
| 253 |
18.3 |
9.3 |
9.0 |
| 598 |
15.6 |
7.0 |
8.6 |
| 2403 |
17.3 |
8.7 |
8.6 |
| 2683 |
>20.0 |
9.9 |
>10.1 |
| 2903 |
19.0 |
9.1 |
9.9 |
| 4254 |
18.5 |
10.4 |
8.1 |
| 4321 |
18.8 |
10.5 |
8.3 |
| 4414 |
>19.5 |
10.1 |
> 9.4 |
| 4490 |
18.8 |
10.2 |
8.6 |
| 5194 |
17.3 |
7.4 |
9.9 |
| 5236 |
18.6 |
10.4 |
8.2 |
| 5457 |
17.0 |
9.9 |
7.1 |
| Irr. |
| LMC |
9.5 |
0.5 |
9.0 |
| SMC |
12.0 |
1.5 |
10.5 |
| 3034 |
>19.5 |
9.0 |
>10.5 |
| 4449 |
17.8 |
9.5 |
8.3 |
| 6822 |
15.8 |
8.5 |
7.3 |
The data are listed in Table XVI and are shown graphically in Figure 10.
The luminosities of the brightest stars are given in photographic
magnitudes. For the Magellanic Clouds, M 33, and N.G.C. 6822, these
were obtained from published star counts. For M 31, 51, 63, 81, 94,
and N.G.C. 2403, they depend upon unpublished counts, for which the
magnitudes were determined by comparisons with Selected Areas. For the
remaining nebulae, the magnitudes of stars were estimated with varying
degrees of precision, but are probably less than 0.5 mag. in error.

Fig. 10.—Relation between total magnitudes of
extra-galactic nebulae and magnitudes of the brightest stars involved.
Differences between total visual magnitudes of nebulae and the
photographic magnitudes of the brightest stars are plotted against
the total magnitudes. The dots represent cases in which the stars
could actually be detected; the incomplete crosses represent cases in
which stars could not be detected, and hence give lower limits for the
magnitude differences. The diagonal line indicates the approximate
limits of observation, fixed by the circumstance that, in general,
stars fainter than 19.5 probably would not be detected on the nebulous
background.
The sloping line to the right in Figure 10 represents the limits
of the observations, for, from a study of the plates themselves,
it appeared improbable that stars fainter than about 19.5 could be
detected with certainty on a nebulous background. Points representing
nebulae in which individual stars could not be found should lie in this
excluded region above the line, and their scatter is presumably{40}
comparable with that of the points actually determined below the line.
When allowance is made for this inaccessible region, the data can be
interpreted as showing a moderate dispersion around the mean ordinate
The range in total magnitudes is sufficiently large in comparison with
the dispersion to lend considerable confidence to the conclusion. The
total range of four, and the average dispersion of less than 1 mag.,
are comparable with those in Table XV and in Figure 7, and agree with
the former in indicating a constant order of absolute magnitude.
The mean absolute magnitude of the brightest stars in the nebulae
listed in Table XV, combined with the mean difference between nebulae
and their brightest stars, furnishes a mean absolute magnitude of –15.3
for the nebulae listed in Table XVI. This differs by only 0.2 mag. from
the average of the nebulae in Table XV, and the mean of the two, –15.2,
can be used as the absolute magnitude of intermediate- and late-type
spirals and irregular nebulae whose apparent magnitudes are brighter
than 10.5. The dispersion is small and can safely be neglected in
statistical investigations.
This is as far as the positive evidence can be followed. For reasons
already given, however, it is presumed that the earlier nebulae,
the elliptical and the early-type spirals, are of the same order of
absolute magnitude as the later. The one elliptical nebula whose
distance is known, M 32, is consistent with this hypothesis.
Conclusions concerning the intrinsic luminosities of the apparently
fainter nebulae are in the nature of extrapolations of the results
found for the brighter objects. When the nebulae are reduced to a
standard type, they are found to be constructed on a single model,
with the total luminosities varying directly as the square of the
diameters. The most general interpretation of this relation is that the
mean surface brightness is constant, but the small range in absolute
magnitudes among the brighter nebulae indicates that, among these
objects at least, the relation merely expresses the operation of the
inverse-square law on comparable objects distributed at different
distances. The actual observed range covered by this restricted
interpretation is from apparent magnitude 0.5 to 10.5. The{41}
homogeneity of the correlation diagrams and the complete absence of
evidence to the contrary justify the extrapolation of the restricted
interpretation to cover the 2 or 3 mag. beyond the limits of actual
observation.
These considerations lead to the hypothesis that the nebulae treated
in the present discussion are all of the same order of absolute
magnitude; in fact, they lend considerable color to the assumption
that extra-galactic nebulae in general are of the same order of
absolute magnitude and, within each class, of the same order of
actual dimensions. Some support to this assumption is found in the
observed absence of individual stars in the apparently fainter
late-type nebulae. If the luminosity of the brightest stars involved
is independent of the total luminosity of a nebula, as is certainly
the case among the brighter objects, then, when no stars brighter than
19.5 are found, the nebulae must in general be brighter than absolute
magnitude mT – 25.8 where mT is the total apparent magnitude. On
this assumption, the faintest of the Holetschek nebulae are brighter
than –12.5 and hence of the same general order as the brighter nebulae.
Once the assumption of a uniform order of luminosity is accepted as a
working hypothesis, the apparent magnitudes become, for statistical
purposes, a measure of the distances. For a mean absolute magnitude of
–15.2, the distance in parsecs is
DIMENSIONS OF EXTRA-GALACTIC NEBULAE
When the distances are known, it is possible to derive actual
dimensions and hence to calibrate the curve in Figure 6, which exhibits
the apparent diameters as a function of type, or stage in the nebular
sequence, for nebulae of a given apparent magnitude. The mean maximum
diameters in parsecs corresponding to the different mean types are
given in Table XVII. For the elliptical nebulae, values are given both
for the statistical mean observed diameters and for the diameter as
calculated for the pure types.
Spirals at the last stage in the observed sequence have diameters of
the order of 3000 parsecs. Assuming 1:10 as the ratio of the two{42}
axes, the corresponding volume is of the order of 1.4×109 cubic
parsecs, and the mean luminosity density is of the order of 7.7
absolute magnitudes per cubic parsec as compared with 8.15 for the
galactic system in the vicinity of the sun. These results agree with
those of Seares who, from a study of surface brightness, concluded
that the galactic system must be placed at the end of, if not actually
outside, the series of known spirals when arranged according to
density.19
TABLE XVII
| Type |
Diameter in Parsecs |
| Obs |
Cal. |
| E0 |
360 |
340 |
| E1 |
430 |
380 |
| E2 |
500 |
430 |
| E3 |
590 |
490 |
| E4 |
700 |
570 |
| E5 |
810 |
680 |
| E6 |
960 |
850 |
| E7 |
1130 |
1130 |
| Type |
Diameter in Parsecs |
| Sa |
1450 |
| Sb |
1900 |
| Sc |
2500 |
| SBa |
1280 |
| SBb |
1320 |
| SBc |
2250 |
| Irr |
1500 |
MASSES OF EXTRA-GALACTIC NEBULAE
Spectroscopic rotations are available for the spirals M 3120 and
N.G.C. 4594,21 and from these it is possible to estimate the masses
on the assumption of orbital rotation around the nucleus. The distances
of the nebulae are involved, however, and this is known accurately
only for M 31; for N.G.C. 4594 it must be estimated from the apparent
luminosity.
Another method of estimating masses is that used by Öpik22 in
deriving his estimate of the distance of M 31. It is based on the
assumption that luminous material in the spirals has about the same
coefficient of emission as the material in the galactic system. Öpik
computed the ratio of luminosity to mass for our own system in{43}
terms of the sun as unity, using Jeans’s value23 for the relative
proportion of luminous to non-luminous material. The relation is
The application of this method of determining orders of masses seems
to be justified, at least in the case of the later-type spirals and
irregular nebulae, by the many analogies with the galactic system
itself. Moreover, when applied to M 31, where the distance is fairly
well known, it leads to a mass of the same order as that derived from
the spectrographic rotation:
MASS OF M 31
| Spectrographic rotation |
3.5×109 ☉ |
| Öpik’s method |
1.6×109 |
The distance of N.G.C. 4594 is unknown, but the assumption that it is a
normal nebula with an absolute magnitude of –15.2 places it at 700,000
parsecs. The orders of the mass by the two methods are then
MASS OF N.G.C. 4594
| Spectrographic rotation |
2.0×109 ☉ |
| Öpik’s method |
2.6×108 |
Here again the resulting masses are of the same order. They can be made
to agree as well as those for M 31 by the not unreasonable assumption
that the absolute luminosity of the nebula is 2 mag. or so brighter
than normal.
Öpik’s method leads to values that are reasonable and fairly consistent
with those obtained by the independent spectrographic method.
Therefore, in the absence of other resources, its use for deriving the
mass of the normal nebula appears to be permissible. The result, 2.6 ×
108 ☉, corresponding to an absolute magnitude of –15.2, is probably
of the right order. The two test cases suggest that this value may be
slightly low, but the data are not sufficient to warrant any empirical
corrections.
NUMBERS OF NEBULAE TO DIFFERENT LIMITING MAGNITUDES
The numbers of nebulae to different limiting magnitudes can be used to
test the constancy of the density function, or, on the hypothesis{44}
of uniform luminosities, to determine the distribution in space. The
nebulae brighter than about the tenth magnitude are known individually.
Those not included in Holetschek’s list are: the Magellanic Clouds, the
two nebulae N.G.C. 55 and 1097, between 9.0 and 9.5 mag., and the seven
nebulae N.G.C. 134, 289, 1365, 1533, 1559, 1792, and 3726, all between
9.5 and 10.0 mag.
A fair estimate of the number between 10.0 and 11.0 mag. can be derived
from a comparison of Holetschek’s list with that of Hardcastle,
an inspection of images on the Franklin-Adams charts and other
photographs, and a correlation between known total magnitudes and
the descriptions of size and brightness in Dreyer’s catalogues. It
appears that very few of these objects were missed by Holetschek in
the northern sky—not more than six of Hardcastle’s nebulae. For the
southern sky, beyond the region observed by Holetschek, the results are
very uncertain, but probable upper and lower limits were determined as
50 and 20, respectively. The brighter nebulae are known to be scarce in
those regions. A mean value of 35 leads to a total 295 for the entire
sky, and this is at least of the proper order.
The number of nebulae between 11.0 and 12.0 mag. can be estimated on
the assumption that the two lists, Holetschek’s and Hardcastle’s,
are about equally complete within this range. They are known to be
comparable for the brighter nebulae, and, moreover, the total numbers
included in the two lists for the same area of the sky, that north
of declination –10°, are very nearly equal—400 as compared with 408.
The percentages of Holetschek’s nebulae included by Hardcastle were
first determined as a function of magnitude. Within the half-magnitude
interval 11.0 to 11.5, for instance, 60 per cent are in Hardcastle’s
list. If the two lists are equally complete and, taken together, are
exhaustive, the total number in the interval will be 1.4 times the
number of Holetschek’s nebulae. The latter is found to be 50 from
smoothed frequency curves of the magnitudes listed in Tables I–IV.
The total number north of –10° is therefore 70. This can be corrected
to represent the entire sky by applying the factor 1.75, which is the
ratio of the total number of Hardcastle’s nebulae, 700, to the number
north of –10°, 400. In this manner a reasonable estimate of 123 is
obtained for the number of nebulae in{45} the entire sky between 11.0
and 11.5 mag. Similarly, between 11.5 and 12.0, where 50 per cent of
Holetschek’s nebulae are included in Hardcastle’s list, the total
number for the entire sky is found to be 236.
The greatest uncertainty in these figures arises from the assumption
that the two lists together are complete to the twelfth magnitude. The
figures are probably too small, but no standards are available by which
they can be corrected. It is believed, however, that the errors are
certainly less than 50 per cent and probably not more than 25 per cent.
This will not be excessive in view of the possible deviations from
uniform distribution where so limited a number of objects is considered.
Beyond 12.0 mag. the lists quickly lose their aspect of completeness
and cannot be used for the present purpose. There are available,
however, the counts by Fath24 of nebulae found on plates of Selected
Areas made with the 60-inch reflector at Mount Wilson. The exposures
were uniformly 60 minutes on fast plates and cover the Areas in
the northern sky down to and including the –15° zone. The limiting
photographic magnitudes for stars average about 18.5. The counts have
been carefully revised by Seares25 and are the basis for his estimate
of 300,000 nebulae in the entire sky down to this limit.
Approximate limiting total magnitudes for the nebulae in two of the
richest fields, S.A. 56 and 80, have been determined from extra-focal
exposures with the 100-inch reflector. The results are 17.7 in each
case, and this, corrected by the normal color-index of such objects,
gives a limiting visual magnitude of about 16.7, which can be used for
comparison with the counts of the brighter nebulae.
The various data are collected in Table XVIII, where the observed
numbers of extra-galactic nebulae to different limits of visual
magnitude are compared with those computed on the assumption of uniform
distribution of objects having a constant absolute luminosity. The
formula used for the computation is
{46}
where the constant is the value of log N for mT = 0. The value —4.45
is found to fit the observational data fairly well.
The agreement between the observed and computed log N over a range of
more than 8 mag. is consistent with the double assumption of uniform
luminosity and uniform distribution or, more generally, indicates that
the density function is independent of the distance.
The systematic decrease in the residuals O – C with decreasing
luminosity is probably within the observational errors, but it may also
be explained as due to a clustering of nebulae in the vicinity of the
galactic system. The cluster in Virgo alone accounts for an appreciable
part. This is a second-order effect in the distribution, however, and
will be discussed at length in a later paper.
TABLE XVIII
Numbers of Nebulae to Various Limits
| mT |
log N* |
O – C |
log D† |
| O |
C |
| 8.5 |
0.85 |
0.65 |
+0.20 |
5.74 |
| 9.0 |
1.08 |
0.95 |
.13 |
5.84 |
| 9.5 |
1.45 |
1.25 |
.20 |
5.94 |
| 10.0 |
1.73 |
1.55 |
.18 |
6.04 |
| 10.5 |
1.95 |
1.85 |
.10 |
6.14 |
| 11.0 |
2.17 |
2.15 |
+ .02 |
6.24 |
| 11.5 |
2.43 |
2.45 |
– .02 |
6.34 |
| 12.0 |
2.70 |
2.75 |
.05 |
6.44 |
| 16.7 |
5.48 |
5.57 |
–0.09 |
7.38 |
| (18.0) |
|
(6.35) |
|
(7.64) |
* Log N = 0.6 mT – 4.45.
† Log D = 0.2 mT + 4.04.
Distances corresponding to the different limiting magnitudes, as
derived from formula (8), are given in the last column of Table XVIII.
The 300,000 nebulae estimated to the limits represented by an
hour’s exposure on fast plates with the 60-inch reflector appear to
be the inhabitants of space out to a distance of the order of 2.4 ×
107 parsecs. The 100-inch reflector, with long exposures under good
conditions, will probably reach the total visual magnitude 18.0, and
this, by a slight extrapolation, is estimated to represent a distance
of the order of 4.4×107 parsecs or 1.4×108 light-years, within
which it is expected that about two million nebulae should be found.
This{47} seems to represent the present boundaries of the observable
region 3 of space.
DENSITY OF SPACE
The data are now available for deriving a value for the order of the
density of space. This is accomplished by means of the formulae for the
numbers of nebulae to a given limiting magnitude and for the distance
in terms of the magnitude. In nebulae per cubic parsec, the density is
This is a lower limit, for the absence of nebulae in the plane of the
Milky Way has been ignored. The current explanation of this phenomenon
in terms of obscuration by dark clouds which encircle the Milky Way
is supported by the extra-galactic nature of the nebulae, their
general similarity to the galactic system, and the frequency with
which peripheral belts of obscuring material are encountered among the
spirals. The known clouds of dark nebulosity are interior features of
our system, and they do not form a continuous belt. In the regions
where they are least conspicuous, however, the extra-galactic nebulae
approach nearest to the plane of the Milky Way, many being found within
10°. This is consistent with the hypothesis of a peripheral belt of
absorption.
The only positive objection which has been urged to this explanation
has been to the effect that the nebular density is a direct function of
galactic latitude. Accumulating evidence26 has failed to confirm this
view and indicates that it is largely due to the influence of the great
cluster in Virgo, some 15° from the north galactic pole. There is no
corresponding concentration in the neighborhood of the south pole.{48}
If an outer belt of absorption is assumed, which, combined with the
known inner clouds, obscures extra-galactic nebulae to a mean distance
of 15° from the galactic plane, the value derived for the density of
space must be increased by nearly 40 per cent. This will not change the
order of the value previously determined and is within the uncertainty
of the masses as derived by Öpik’s method. The new value is then
The corresponding mean distance between nebulae is of the order of
570,000 parsecs, although in several of the clusters the distances
between members appear to be a tenth of this amount or less.
The density can be reduced to absolute units by substituting the value
for the mean mass of a nebula, 2.6×108 ☉. Then, since the mass of
the sun in grams is 2×1033 and 1 parsec is 3.1×1018 cm,
This must be considered as a lower limit, for loose material scattered
between the systems is entirely ignored. There are no means of
estimating the order of the necessary correction. No positive evidence
of absorption by inter-nebular material, either selective or general,
has been found, nor should we expect to find it unless the amount of
this material is many times that which is concentrated in the systems.
THE FINITE UNIVERSE OF GENERAL RELATIVITY
The mean density of space can be used to determine the dimensions of
the finite but boundless universe of general relativity. De Sitter27
made the calculations some years ago, but used values for the density,
10–26 and greater, which are of an entirely different order from
that indicated by the present investigations. As a consequence, the
various dimensions, both for spherical and for elliptical space, were
small as compared with the range of existing instruments.
For the present purpose, the simplified equations which Einstein has
derived for a spherically curved space can be used.28 When{49} R, V,
M, and ρ represent the radius of curvature, volume, mass, and density,
and k and c are the gravitational constant and the velocity of light,
Substituting the value found for ρ, 1.5×10–31, the dimensions
become
The mass corresponds to 3.5×1015 normal nebulae.
The distance to which the 100-inch reflector should detect the normal
nebula was found to be of the order of 4.4×1075 parsecs, or about
1⁄600 the radius of curvature. Unusually bright nebulae, such as M
31, could be photographed at several times this distance, and with
reasonable increases in the speed of plates and size of telescopes it
may become possible to observe an appreciable fraction of the Einstein
universe.
Mount Wilson Observatory
September 1926
| e |
Ce |
5 log (1 – e) |
C0 |
Res. |
| 0 |
10.30 |
0.0 |
10.30 |
–0.14 |
| 1 |
10.65 |
– .23 |
10.42 |
– .02 |
| 2 |
11.00 |
.48 |
10.52 |
+ .10 |
| 3 |
11.35 |
0.78 |
10.57 |
+ .13 |
| 4 |
11.70 |
1.11 |
10.59 |
+ .15 |
| 5 |
12.05 |
1.50 |
10.55 |
+ .11 |
| 6 |
12.40 |
1.99 |
10.41 |
– .03 |
| 7 |
12.75 |
–2.62 |
10.13 |
–0.31 |
| Mean |
|
|
10.44 |
0.12 |
Transcriber’s Notes
Text notes:
- For the HTML version, page numbers of the original printed text
are displayed within braces to the side of the text. The numbers
have been remapped to start at page 1.
- Footnotes have been renumbered and moved to the end of the paper.
- Tables have been moved to avoid splitting paragraphs. In some cases
the tables have been reconfigured or split in order to work better
with e-readers. As a result, page numbers may not be accurate
for tables and adjacent text.
- Some of the mathematical equations were created using TeX notation
that was converted into SVG images via the tex2svg function in
MathJax. The Tex notation is contained in the plain text version.
- Except as mentioned above every effort has been made to replicate
this text as faithfully as possible, including non-standard
punctuation, inconsistently hyphenated words, etc.
- The original printed text is available from HathiTrust at:
https://hdl.handle.net/2027/uc1.b3805680 (see pg 353).
- The outline “CLASSIFICATION OF NEBULAE” starting on page 3 lists
N.G.C. 2117 as a type E7 nebula. The version of this paper printed in
Contributions from the Mount Wilson Observatory No. 324
lists N.G.C 3115. Otherwise the papers are essentially identical.
*** END OF THE PROJECT GUTENBERG EBOOK EXTRA-GALACTIC NEBULAE ***
Updated editions will replace the previous one—the old editions will
be renamed.
Creating the works from print editions not protected by U.S. copyright
law means that no one owns a United States copyright in these works,
so the Foundation (and you!) can copy and distribute it in the United
States without permission and without paying copyright
royalties. Special rules, set forth in the General Terms of Use part
of this license, apply to copying and distributing Project
Gutenberg™ electronic works to protect the PROJECT GUTENBERG™
concept and trademark. Project Gutenberg is a registered trademark,
and may not be used if you charge for an eBook, except by following
the terms of the trademark license, including paying royalties for use
of the Project Gutenberg trademark. If you do not charge anything for
copies of this eBook, complying with the trademark license is very
easy. You may use this eBook for nearly any purpose such as creation
of derivative works, reports, performances and research. Project
Gutenberg eBooks may be modified and printed and given away—you may
do practically ANYTHING in the United States with eBooks not protected
by U.S. copyright law. Redistribution is subject to the trademark
license, especially commercial redistribution.
START: FULL LICENSE
THE FULL PROJECT GUTENBERG LICENSE
PLEASE READ THIS BEFORE YOU DISTRIBUTE OR USE THIS WORK
To protect the Project Gutenberg™ mission of promoting the free
distribution of electronic works, by using or distributing this work
(or any other work associated in any way with the phrase “Project
Gutenberg”), you agree to comply with all the terms of the Full
Project Gutenberg™ License available with this file or online at
www.gutenberg.org/license.
Section 1. General Terms of Use and Redistributing Project Gutenberg™ electronic works
1.A. By reading or using any part of this Project Gutenberg™
electronic work, you indicate that you have read, understand, agree to
and accept all the terms of this license and intellectual property
(trademark/copyright) agreement. If you do not agree to abide by all
the terms of this agreement, you must cease using and return or
destroy all copies of Project Gutenberg™ electronic works in your
possession. If you paid a fee for obtaining a copy of or access to a
Project Gutenberg™ electronic work and you do not agree to be bound
by the terms of this agreement, you may obtain a refund from the person
or entity to whom you paid the fee as set forth in paragraph 1.E.8.
1.B. “Project Gutenberg” is a registered trademark. It may only be
used on or associated in any way with an electronic work by people who
agree to be bound by the terms of this agreement. There are a few
things that you can do with most Project Gutenberg™ electronic works
even without complying with the full terms of this agreement. See
paragraph 1.C below. There are a lot of things you can do with Project
Gutenberg™ electronic works if you follow the terms of this
agreement and help preserve free future access to Project Gutenberg™
electronic works. See paragraph 1.E below.
1.C. The Project Gutenberg Literary Archive Foundation (“the
Foundation” or PGLAF), owns a compilation copyright in the collection
of Project Gutenberg™ electronic works. Nearly all the individual
works in the collection are in the public domain in the United
States. If an individual work is unprotected by copyright law in the
United States and you are located in the United States, we do not
claim a right to prevent you from copying, distributing, performing,
displaying or creating derivative works based on the work as long as
all references to Project Gutenberg are removed. Of course, we hope
that you will support the Project Gutenberg™ mission of promoting
free access to electronic works by freely sharing Project Gutenberg™
works in compliance with the terms of this agreement for keeping the
Project Gutenberg™ name associated with the work. You can easily
comply with the terms of this agreement by keeping this work in the
same format with its attached full Project Gutenberg™ License when
you share it without charge with others.
1.D. The copyright laws of the place where you are located also govern
what you can do with this work. Copyright laws in most countries are
in a constant state of change. If you are outside the United States,
check the laws of your country in addition to the terms of this
agreement before downloading, copying, displaying, performing,
distributing or creating derivative works based on this work or any
other Project Gutenberg™ work. The Foundation makes no
representations concerning the copyright status of any work in any
country other than the United States.
1.E. Unless you have removed all references to Project Gutenberg:
1.E.1. The following sentence, with active links to, or other
immediate access to, the full Project Gutenberg™ License must appear
prominently whenever any copy of a Project Gutenberg™ work (any work
on which the phrase “Project Gutenberg” appears, or with which the
phrase “Project Gutenberg” is associated) is accessed, displayed,
performed, viewed, copied or distributed:
This eBook is for the use of anyone anywhere in the United States and most
other parts of the world at no cost and with almost no restrictions
whatsoever. You may copy it, give it away or re-use it under the terms
of the Project Gutenberg License included with this eBook or online
at
www.gutenberg.org. If you
are not located in the United States, you will have to check the laws
of the country where you are located before using this eBook.
1.E.2. If an individual Project Gutenberg™ electronic work is
derived from texts not protected by U.S. copyright law (does not
contain a notice indicating that it is posted with permission of the
copyright holder), the work can be copied and distributed to anyone in
the United States without paying any fees or charges. If you are
redistributing or providing access to a work with the phrase “Project
Gutenberg” associated with or appearing on the work, you must comply
either with the requirements of paragraphs 1.E.1 through 1.E.7 or
obtain permission for the use of the work and the Project Gutenberg™
trademark as set forth in paragraphs 1.E.8 or 1.E.9.
1.E.3. If an individual Project Gutenberg™ electronic work is posted
with the permission of the copyright holder, your use and distribution
must comply with both paragraphs 1.E.1 through 1.E.7 and any
additional terms imposed by the copyright holder. Additional terms
will be linked to the Project Gutenberg™ License for all works
posted with the permission of the copyright holder found at the
beginning of this work.
1.E.4. Do not unlink or detach or remove the full Project Gutenberg™
License terms from this work, or any files containing a part of this
work or any other work associated with Project Gutenberg™.
1.E.5. Do not copy, display, perform, distribute or redistribute this
electronic work, or any part of this electronic work, without
prominently displaying the sentence set forth in paragraph 1.E.1 with
active links or immediate access to the full terms of the Project
Gutenberg™ License.
1.E.6. You may convert to and distribute this work in any binary,
compressed, marked up, nonproprietary or proprietary form, including
any word processing or hypertext form. However, if you provide access
to or distribute copies of a Project Gutenberg™ work in a format
other than “Plain Vanilla ASCII” or other format used in the official
version posted on the official Project Gutenberg™ website
(www.gutenberg.org), you must, at no additional cost, fee or expense
to the user, provide a copy, a means of exporting a copy, or a means
of obtaining a copy upon request, of the work in its original “Plain
Vanilla ASCII” or other form. Any alternate format must include the
full Project Gutenberg™ License as specified in paragraph 1.E.1.
1.E.7. Do not charge a fee for access to, viewing, displaying,
performing, copying or distributing any Project Gutenberg™ works
unless you comply with paragraph 1.E.8 or 1.E.9.
1.E.8. You may charge a reasonable fee for copies of or providing
access to or distributing Project Gutenberg™ electronic works
provided that:
• You pay a royalty fee of 20% of the gross profits you derive from
the use of Project Gutenberg™ works calculated using the method
you already use to calculate your applicable taxes. The fee is owed
to the owner of the Project Gutenberg™ trademark, but he has
agreed to donate royalties under this paragraph to the Project
Gutenberg Literary Archive Foundation. Royalty payments must be paid
within 60 days following each date on which you prepare (or are
legally required to prepare) your periodic tax returns. Royalty
payments should be clearly marked as such and sent to the Project
Gutenberg Literary Archive Foundation at the address specified in
Section 4, “Information about donations to the Project Gutenberg
Literary Archive Foundation.”
• You provide a full refund of any money paid by a user who notifies
you in writing (or by e-mail) within 30 days of receipt that s/he
does not agree to the terms of the full Project Gutenberg™
License. You must require such a user to return or destroy all
copies of the works possessed in a physical medium and discontinue
all use of and all access to other copies of Project Gutenberg™
works.
• You provide, in accordance with paragraph 1.F.3, a full refund of
any money paid for a work or a replacement copy, if a defect in the
electronic work is discovered and reported to you within 90 days of
receipt of the work.
• You comply with all other terms of this agreement for free
distribution of Project Gutenberg™ works.
1.E.9. If you wish to charge a fee or distribute a Project
Gutenberg™ electronic work or group of works on different terms than
are set forth in this agreement, you must obtain permission in writing
from the Project Gutenberg Literary Archive Foundation, the manager of
the Project Gutenberg™ trademark. Contact the Foundation as set
forth in Section 3 below.
1.F.
1.F.1. Project Gutenberg volunteers and employees expend considerable
effort to identify, do copyright research on, transcribe and proofread
works not protected by U.S. copyright law in creating the Project
Gutenberg™ collection. Despite these efforts, Project Gutenberg™
electronic works, and the medium on which they may be stored, may
contain “Defects,” such as, but not limited to, incomplete, inaccurate
or corrupt data, transcription errors, a copyright or other
intellectual property infringement, a defective or damaged disk or
other medium, a computer virus, or computer codes that damage or
cannot be read by your equipment.
1.F.2. LIMITED WARRANTY, DISCLAIMER OF DAMAGES - Except for the “Right
of Replacement or Refund” described in paragraph 1.F.3, the Project
Gutenberg Literary Archive Foundation, the owner of the Project
Gutenberg™ trademark, and any other party distributing a Project
Gutenberg™ electronic work under this agreement, disclaim all
liability to you for damages, costs and expenses, including legal
fees. YOU AGREE THAT YOU HAVE NO REMEDIES FOR NEGLIGENCE, STRICT
LIABILITY, BREACH OF WARRANTY OR BREACH OF CONTRACT EXCEPT THOSE
PROVIDED IN PARAGRAPH 1.F.3. YOU AGREE THAT THE FOUNDATION, THE
TRADEMARK OWNER, AND ANY DISTRIBUTOR UNDER THIS AGREEMENT WILL NOT BE
LIABLE TO YOU FOR ACTUAL, DIRECT, INDIRECT, CONSEQUENTIAL, PUNITIVE OR
INCIDENTAL DAMAGES EVEN IF YOU GIVE NOTICE OF THE POSSIBILITY OF SUCH
DAMAGE.
1.F.3. LIMITED RIGHT OF REPLACEMENT OR REFUND - If you discover a
defect in this electronic work within 90 days of receiving it, you can
receive a refund of the money (if any) you paid for it by sending a
written explanation to the person you received the work from. If you
received the work on a physical medium, you must return the medium
with your written explanation. The person or entity that provided you
with the defective work may elect to provide a replacement copy in
lieu of a refund. If you received the work electronically, the person
or entity providing it to you may choose to give you a second
opportunity to receive the work electronically in lieu of a refund. If
the second copy is also defective, you may demand a refund in writing
without further opportunities to fix the problem.
1.F.4. Except for the limited right of replacement or refund set forth
in paragraph 1.F.3, this work is provided to you ‘AS-IS’, WITH NO
OTHER WARRANTIES OF ANY KIND, EXPRESS OR IMPLIED, INCLUDING BUT NOT
LIMITED TO WARRANTIES OF MERCHANTABILITY OR FITNESS FOR ANY PURPOSE.
1.F.5. Some states do not allow disclaimers of certain implied
warranties or the exclusion or limitation of certain types of
damages. If any disclaimer or limitation set forth in this agreement
violates the law of the state applicable to this agreement, the
agreement shall be interpreted to make the maximum disclaimer or
limitation permitted by the applicable state law. The invalidity or
unenforceability of any provision of this agreement shall not void the
remaining provisions.
1.F.6. INDEMNITY - You agree to indemnify and hold the Foundation, the
trademark owner, any agent or employee of the Foundation, anyone
providing copies of Project Gutenberg™ electronic works in
accordance with this agreement, and any volunteers associated with the
production, promotion and distribution of Project Gutenberg™
electronic works, harmless from all liability, costs and expenses,
including legal fees, that arise directly or indirectly from any of
the following which you do or cause to occur: (a) distribution of this
or any Project Gutenberg™ work, (b) alteration, modification, or
additions or deletions to any Project Gutenberg™ work, and (c) any
Defect you cause.
Section 2. Information about the Mission of Project Gutenberg™
Project Gutenberg™ is synonymous with the free distribution of
electronic works in formats readable by the widest variety of
computers including obsolete, old, middle-aged and new computers. It
exists because of the efforts of hundreds of volunteers and donations
from people in all walks of life.
Volunteers and financial support to provide volunteers with the
assistance they need are critical to reaching Project Gutenberg™’s
goals and ensuring that the Project Gutenberg™ collection will
remain freely available for generations to come. In 2001, the Project
Gutenberg Literary Archive Foundation was created to provide a secure
and permanent future for Project Gutenberg™ and future
generations. To learn more about the Project Gutenberg Literary
Archive Foundation and how your efforts and donations can help, see
Sections 3 and 4 and the Foundation information page at www.gutenberg.org.
Section 3. Information about the Project Gutenberg Literary Archive Foundation
The Project Gutenberg Literary Archive Foundation is a non-profit
501(c)(3) educational corporation organized under the laws of the
state of Mississippi and granted tax exempt status by the Internal
Revenue Service. The Foundation’s EIN or federal tax identification
number is 64-6221541. Contributions to the Project Gutenberg Literary
Archive Foundation are tax deductible to the full extent permitted by
U.S. federal laws and your state’s laws.
The Foundation’s business office is located at 809 North 1500 West,
Salt Lake City, UT 84116, (801) 596-1887. Email contact links and up
to date contact information can be found at the Foundation’s website
and official page at www.gutenberg.org/contact
Section 4. Information about Donations to the Project Gutenberg Literary Archive Foundation
Project Gutenberg™ depends upon and cannot survive without widespread
public support and donations to carry out its mission of
increasing the number of public domain and licensed works that can be
freely distributed in machine-readable form accessible by the widest
array of equipment including outdated equipment. Many small donations
($1 to $5,000) are particularly important to maintaining tax exempt
status with the IRS.
The Foundation is committed to complying with the laws regulating
charities and charitable donations in all 50 states of the United
States. Compliance requirements are not uniform and it takes a
considerable effort, much paperwork and many fees to meet and keep up
with these requirements. We do not solicit donations in locations
where we have not received written confirmation of compliance. To SEND
DONATIONS or determine the status of compliance for any particular state
visit
www.gutenberg.org/donate.
While we cannot and do not solicit contributions from states where we
have not met the solicitation requirements, we know of no prohibition
against accepting unsolicited donations from donors in such states who
approach us with offers to donate.
International donations are gratefully accepted, but we cannot make
any statements concerning tax treatment of donations received from
outside the United States. U.S. laws alone swamp our small staff.
Please check the Project Gutenberg web pages for current donation
methods and addresses. Donations are accepted in a number of other
ways including checks, online payments and credit card donations. To
donate, please visit: www.gutenberg.org/donate
Section 5. General Information About Project Gutenberg™ electronic works
Professor Michael S. Hart was the originator of the Project
Gutenberg™ concept of a library of electronic works that could be
freely shared with anyone. For forty years, he produced and
distributed Project Gutenberg™ eBooks with only a loose network of
volunteer support.
Project Gutenberg™ eBooks are often created from several printed
editions, all of which are confirmed as not protected by copyright in
the U.S. unless a copyright notice is included. Thus, we do not
necessarily keep eBooks in compliance with any particular paper
edition.
Most people start at our website which has the main PG search
facility:
www.gutenberg.org.
This website includes information about Project Gutenberg™,
including how to make donations to the Project Gutenberg Literary
Archive Foundation, how to help produce our new eBooks, and how to
subscribe to our email newsletter to hear about new eBooks.
where C varies progressively from type to type, indicating a variation
in diameter for a given magnitude or vice versa. By applying
corrections to C, the nebulae can be reduced to a standard type and
then a single formula expresses the relation for all nebulae from
the Magellanic Clouds to the faintest that can be classified. When
the minor diameter is used, the value of C is approximately constant
throughout the entire sequence. The coefficient of log d corresponds
with the inverse-square law, which suggests that the nebulae are all of
the same order of absolute luminosity and that apparent magnitudes are
measures of distance. This hypothesis is supported by similar results
for the nuclear magnitudes and the magnitudes of the brightest stars
involved, and by the small range in luminosities among nebulae whose
distances are already known.
where mT is the total apparent magnitude. This leads to mean values
for absolute dimensions at various stages in the sequence of types.
Masses appear to be of the order of 2.6×108 ☉.























