
MARY SOMERVILLE
J. COOPER Sc.
The Project Gutenberg EBook of On the Connexion of the Physical Sciences, by Mary Somerville This eBook is for the use of anyone anywhere at no cost and with almost no restrictions whatsoever. You may copy it, give it away or re-use it under the terms of the Project Gutenberg License included with this eBook or online at www.gutenberg.org/license Title: On the Connexion of the Physical Sciences Author: Mary Somerville Release Date: August 21, 2016 [EBook #52869] Language: English Character set encoding: UTF-8 *** START OF THIS PROJECT GUTENBERG EBOOK CONNEXION OF THE PHYSICAL SCIENCES *** Produced by Sonya Schermann and the Online Distributed Proofreading Team at http://www.pgdp.net (This file was produced from images generously made available by The Internet Archive)
This book uses some unusual characters, such as those representing the constellation Aries (♈) and Libra (♎). These characters may fail to display correctly if the font you are using does not support them.
Some corrections have been made to the printed text. These are listed in a second transcriber’s note at the end of the text.

MARY SOMERVILLE
J. COOPER Sc.
“No natural phenomenon can be adequately studied in itself alone—but, to be understood, it must be considered as it stands connected with all Nature.”—Bacon.
Florence, Nov. 1, 1858.
Introduction
Attraction of a Sphere—Form of Celestial Bodies—Terrestrial Gravitation retains the Moon in her Orbit—The Heavenly Bodies move in Conic Sections—Gravitation Proportional to Mass—Gravitation of the Particles of Matter—Figure of the Planets—How it affects the Motions of their Satellites—Rotation and Translation impressed by the same Impulse—Motion of the Sun and Solar System
Elliptical Motion—Mean and True Motion—Equinoctial—Ecliptic—Equinoxes—Mean and True Longitude—Equation of Centre—Inclination of the Orbits of Planets—Celestial Latitude—Nodes—Elements of an Orbit—Undisturbed or Elliptical Orbits—Great Inclination of the Orbits of the New Planets—Universal Gravitation the Cause of Perturbations in the Motions of the Heavenly Bodies—Problem of the Three Bodies—Stability of Solar System depends upon the Primitive Momentum of the Bodies
Perturbations, Periodic and Secular—Disturbing Action equivalent to three Partial Forces—Tangential Force the cause of the Periodic Inequalities in Longitude, and Secular Inequalities in the Form and Position of the Orbit in its own Plane—Radial Force the cause of Variations in the Planet’s Distance from the Sun—It combines with the Tangential Force to produce the Secular Variations in the Form and Position of the Orbit in its own Plane—Perpendicular Force the cause of Periodic Perturbations in Latitude, and Secular Variations in the Position of the Orbit with regard to the Plane of the Ecliptic—Mean Motion and Major Axis Invariable—Stability of System—Effects of a Resisting Medium—Invariable Plane of the Solar System and of the Universe—Great Inequality of Jupiter and Saturn
Theory of Jupiter’s Satellites—Effects of the Figure of Jupiter upon his Satellites—Position of their Orbits—Singular Laws among the Motions of the first Three Satellites—Eclipses of the Satellites—Velocity of Light—Aberration—Ethereal Medium—Satellites of Saturn and Uranus
Lunar Theory—Periodic Perturbations of the Moon—Equation of Centre—Evection—Variation—Annual Equation—Direct and Indirect Action of Planets—The Moon’s Action on the Earth disturbs her own Motion—Excentricity and Inclination of Lunar Orbit invariable—Acceleration—Secular Variation in Nodes and Perigee—Motion of Nodes and Perigee inseparably connected with the Acceleration—Nutation of Lunar Orbit—Form and Internal Structure of the Earth determined from it—Lunar, Solar, and Planetary Eclipses—Occultations and Lunar Distances—Mean Distance of the Sun from the Earth obtained from Lunar Theory—Absolute Distances of the Planets, how found
Form of the Earth and Planets—Figure of a Homogeneous Spheroid in Rotation—Figure of a Spheroid of variable Density—Figure of the Earth, supposing it to be an Ellipsoid of Revolution—Mensuration of a Degree of the Meridian—Compression and Size of the Earth from Degrees of Meridian—Figure of Earth from the Pendulum
Parallax—Lunar Parallax found from Direct Observation—Solar Parallax deduced from the Transit of Venus—Distance of the Sun from the Earth—Annual Parallax—Distance of the Fixed Stars
Masses of Planets that have no Satellites determined from their Perturbations—Masses of the others obtained from the Motions of their Satellites—Masses of the Sun, the Earth, of Jupiter and of the Jovial System—Mass of the Moon—Real Diameters of Planets, how obtained—Size of Sun, Densities of the Heavenly Bodies—Formation of Astronomical Tables—Requisite Data and Means of obtaining them
Rotation of the Sun and Planets—Saturn’s Rings—Periods of the Rotation of the Moon and other Satellites equal to the Periods of their Revolutions—Form of Lunar Spheroid—Libration, Aspect, and Constitution of the Moon—Rotation of Jupiter’s Satellites
Rotation of the Earth invariable—Decrease in the Earth’s mean Temperature—Earth originally in a state of Fusion—Length of Day constant—Decrease of Temperature ascribed by Sir John Herschel to the variation in the Excentricity of the Terrestrial Orbit—Difference in the Temperature of the two Hemispheres erroneously ascribed to the Excess in the Length of Spring and Summer in the Southern Hemisphere; attributed by Sir Charles Lyell to the Operation of existing Causes—Three principal Axes of Rotation—Position of the Axis of Rotation on the Surface of the Earth invariable—Ocean not sufficient to restore the Equilibrium of the Earth if deranged—Its Density and mean Depth—Internal Structure of the Earth
Precession and Nutation—Their Effects on the Apparent Places of the Fixed Stars
Mean and Apparent Sidereal Time—Mean and Apparent Solar Time—Equation of Time—English and French Subdivisions of Time—Leap Year—Christian Era—Equinoctial Time—Remarkable Eras depending upon the Position of the Solar Perigee—Inequality of the Lengths of the Seasons in the two Hemispheres—Application of Astronomy to Chronology—English and French Standards of Weights and Measures
Tides—Forces that produce them—Origin and Course of Tidal Wave—Its Speed—Three kinds of Oscillations in the Ocean—The Semidiurnal Tides—Equinoctial Tides—Effects of the Declination of the Sun and Moon—Theory insufficient without Observation—Direction of the Tidal Wave—Height of Tides—Mass of Moon obtained from her Action on the Tides—Interference of Undulations—Impossibility of a Universal Inundation—Currents
Molecular Forces—Permanency of the ultimate Particles of Matter—Interstices—Mossotti’s Theory—Rankin’s Theory of Molecular Vortices—Gases reduced to Liquids by Pressure—Gravitation of Particles—Cohesion—Crystallization—Cleavage—Isomorphism—Minuteness of the Particles—Height of Atmosphere—Chemical Affinity—Definite Proportions and Relative Weights of Atoms—Faraday’s Discovery with regard to Affinity—Capillary Attraction
Analysis of the Atmosphere—Its pressure—Law of Decrease in Density—Law of Decrease in Temperature—Measurement of Heights by the Barometer—Extent of the Atmosphere—Barometrical Variations—Oscillations—Trade-Winds—Cloud-Ring—Monsoons—Rotation of Winds—Laws of Hurricanes
Sound—Propagation of Sound illustrated by a Field of Standing Corn—Nature of Waves—Propagation of Sound through the Atmosphere—Intensity—Noises—A Musical Sound—Quality—Pitch—Extent of Human Hearing—Velocity of Sound in Air, Water, and Solids—Causes of the Obstruction of Sound—Law of its Intensity—Reflection of Sound—Echoes—Thunder—Refraction of Sound—Interference of Sounds
Vibration of Musical Strings—Harmonic Sounds—Nodes—Vibration of Air in Wind-Instruments—Vibration of Solids—Vibrating Plates—Bells—Harmony—Sounding Boards—Forced Vibrations—Resonance—Speaking Machines
Refraction—Astronomical Refraction and its Laws—Formation of Tables of Refraction—Terrestrial Refraction—Its Quantity—Instances of Extraordinary Refraction—Reflection—Instances of Extraordinary Reflection—Loss of Light by the Absorbing Power of the Atmosphere—Apparent Magnitude of Sun and Moon in the Horizon
Constitution of Light according to Sir Isaac Newton—Absorption of Light—Colours of Bodies—Constitution of Light according to Sir David Brewster—New Colours—Fraunhofer’s Dark Lines—Dispersion of Light—The Achromatic Telescope—Homogeneous Light—Accidental and Complementary Colours—M. Plateau’s Experiments and Theory of Accidental Colours
Interference of Light—Undulatory Theory of Light—Propagation of Light—Newton’s Rings—Measurement of the Length of the Waves of Light, and of the Frequency of the Vibrations of Ether for each Colour—Newton’s Scale of Colours—Diffraction of Light—Sir John Herschel’s Theory of the Absorption of Light—Refraction and Reflection of Light
Polarization of Light—Defined—Polarization by Refraction—Properties of the Tourmaline—Double Refraction—All doubly Refracted Light is Polarized—Properties of Iceland Spar—Tourmaline absorbs one of the two Refracted Rays—Undulations of Natural Light—Undulations of Polarized Light—The Optic Axes of Crystals—M. Fresnel’s Discoveries on the Rays passing along the Optic Axis—Polarization by Reflection
Phenomena exhibited by the Passage of Polarized Light through Mica and Sulphate of Lime—The Coloured Images produced by Polarized Light passing through Crystals having one and two Optic Axes—Circular Polarization—Elliptical Polarization—Discoveries of MM. Biot, Fresnel, and Professor Airy—Coloured Images produced by the Interference of Polarized Rays—Fluorescence
Objections to the Undulatory Theory, from a difference in the Action of Sound and Light under the same circumstances, removed—The Dispersion of Light according to the Undulatory Theory—Arago’s final proof that the Undulatory Theory is the Law of Nature
Chemical or Photographic Rays of Solar Spectrum—Scheele, Ritter, and Wollaston’s Discoveries—Wedgwood’s and Sir Humphry Davy’s Photographic Pictures—The Calotype—The Daguerreotype—The Chromatype—The Cyanotype—Collodion—Sir John Herschel’s Discoveries in the Chemical Spectrum—M. Becquerel’s Discoveries of Inactive Lines in ditto—Thermic Spectrum—Phosphoric Spectrum—Electrical Properties—Parathermic Rays—Moser and Hunt’s Experiments—General Structure and antagonist Properties of Solar Spectrum—Defracted Spectrum
Size and Constitution of the Sun—The Solar Spots—Intensity of the Sun’s Light and Heat—The Sun’s Atmosphere—His influence on the Planets—Atmospheres of the Planets—The Moon has none—Lunar heat—The Differential Telescope—Temperature of Space—Internal Heat of the Earth—Zone of constant Temperature—Increase of Heat with the Depth—Central Heat—Volcanic Action—Quantity of Heat received from the Sun—Isogeothermal Lines—Line of Perpetual Congelation—Climate—Isothermal Lines—Same quantity of Heat annually received and radiated by the Earth
Influence of Temperature on Vegetation—Vegetation varies with the Latitude and Height above the Sea—Geographical Distribution of Land Plants—Distribution of Marine Plants—Corallines, Shell-fish, Reptiles, Insects, Birds, and Quadrupeds—Varieties of Mankind, yet identity of Species
Terrestrial Heat—Radiation—Transmission—Melloni’s experiments—Heat in Solar Spectrum—Polarization of Heat—Nature of Heat—Absorptions—Dew—Rain—Combustion—Expansion—Compensation Pendulum—Transmission through Crystals—Propagation—Dynamic Theory of Heat—Mechanical equivalent of Heat—Latent Heat is the Force of Expansion—Steam—Work performed by Heat—Conservation of Force—Mechanical Power in the Tides—Dynamical Power of Light—Analogy between Light, Heat, and Sound
Common or Static Electricity, or Electricity of Tension—A Dual Power—Methods of exciting it—Attraction and Repulsion—Conduction—Electrics and Non-electrics—Induction—Dielectrics—Tension—Law of the Electric Force—Distribution—Laws of Distribution—Heat of Electricity—Electrical Light and its Spectrum—Velocity—Atmospheric Electricity—Its cause—Electric Clouds—Violent effects of Lightning—Back Stroke—Electric Glow—Phosphorescence
Voltaic Electricity—The Voltaic Battery—Intensity—Quantity—Static Electricity, and Electricity in Motion—Luminous Effects—Mr. Grove on the Electric Arc and Light—Decomposition of Water—Formation of Crystals by Voltaic Electricity—Photo-galvanic Engraving—Conduction—Heat of Voltaic Electricity—Electric Fish
Discovery of Electro-magnetism—Deflection of the Magnetic Needle by a Current of Electricity—Direction of the Force—Rotatory Motion by Electricity—Rotation of a Wire and a Magnet—Rotation of a Magnet about its Axis—Of Mercury and Water—Electro-Magnetic Cylinder or Helix—Suspension of a Needle in a Helix—Electro-Magnetic Induction—Temporary Magnets—The Galvanometer
Electro-Dynamics—Reciprocal Action of Electric Currents—Identity of Electro-Dynamic Cylinders and Magnets—Differences between the Action of Voltaic Electricity and Electricity of Tension—Effects of a Voltaic Current—Ampère’s Theory—Dr. Faraday’s Experiment of Electrifying and Magnetising a Ray of Light
Magneto-Electricity—Volta-Electric Induction—Magneto-Electric Induction—Identity in the Action of Electricity and Magnetism—Description of a Magneto-Electric Apparatus and its Effects—Identity of Magnetism and Electricity—The Submarine Telegraph
Electricity produced by Rotation—Direction of the Currents—Electricity from the Rotation of a Magnet—M. Arago’s Experiment explained—Rotation of a Plate of Iron between the Poles of a Magnet—Relation of Substances to Magnets of three Kinds—Thermo-Electricity
Magnetism a Dual Power—Antithetic Character of Paramagnetism and Diamagnetism—The Earth Paramagnetic—Properties of Paramagnetic Bodies—Polarity—Induction—Lines of Magnetic Force—Currents of Electricity induced by them—Proved to be Closed Curves—Analogy and Identity of Electricity and Magnetism—Terrestrial Magnetism—Mean Values of the Three Magnetic Elements—Their Variations in Double Progression proved to consist of Two Superposed Variations—Discovery of the Periodicity of the Magnetic Storms—The Decennial Period of the Magnetic Elements the same with that of the Solar Spots—Magnetism of the Atmosphere—Diamagnetism—Action of Electro-Magnetism on Paramagnetic, Diamagnetic Bodies, and on Copper, very different—Proof of Diamagnetic Polarity and Induction—Magnecrystallic Action—Effects of Compression, Heat, and Cleavage on Magnetic Bodies—Mutual Dependence of Light, Heat, Electricity, &c. &c.—The Conservation of Force and the Permanency of Matter Primary Laws of Nature—Definition of Gravity not according to that Law—Gravity only the Residual Force of a Universal Power—Magnetism of the Ethereal Medium
Ethereal Medium—Comets—Do not disturb the Solar System—Their Orbits and Disturbances—M. Faye’s Comet probably the same with Lexel’s—Periods of other three known—Acceleration in the mean Motions of Encke’s and Biela’s Comets—The Shock of a Comet—Disturbing Action of the Earth and Planets on Encke’s and Biela’s Comets—Velocity of Comets—The Comet of 1264—The great Comet of 1343—Physical Constitution—Shine by borrowed Light—Estimation of their Number
The Fixed Stars—Their Number—The Milky Way—Double Stars—Binary Systems—Their Orbits and Periodic Times—Colours of the Stars—Stars that have vanished—Variable Stars—Variation in Sun’s Light—Parallax and Distances of the Fixed Stars—Masses of the Stars—Comparative Light of the Stars—Proper Motions of the Stars—Apparent Motions of the Stars—Motion and Velocity of the Sun and Solar System—The Nebulæ—Their Number—Catalogue of them—Consist of Two Classes—Diffuse Nebulæ—Definitely formed Nebulæ—Globular Clusters—Splendour of Milky Way—Distribution of the Nebulæ—The Magellanic Clouds—Nebulæ round η Argûs—Constitution of Nebulæ, and the Forces that maintain them—Meteorites and Shooting Stars
Diffusion of Matter through Space—Gravitation—Its Velocity—Simplicity of its Laws—Gravitation independent of the Magnitude and Distances of the Bodies—Not impeded by the intervention of any Substance—Its Intensity invariable—General Laws—Recapitulation and Conclusion
Notes
Index
Science, regarded as the pursuit of truth, must ever afford occupation of consummate interest, and subject of elevated meditation. The contemplation of the works of creation elevates the mind to the admiration of whatever is great and noble; accomplishing the object of all study, which, in the eloquent language of Sir James Mackintosh, “is to inspire the love of truth, of wisdom, of beauty—especially of goodness, the highest beauty—and of that supreme and eternal Mind, which contains all truth and wisdom, all beauty and goodness. By the love or delightful contemplation and pursuit of these transcendent aims, for their own sake only, the mind of man is raised from low and perishable objects, and prepared for those high destinies which are appointed for all those who are capable of them.”
Astronomy affords the most extensive example of the connection of the physical sciences. In it are combined the sciences of number and quantity, of rest and motion. In it we perceive the operation of a force which is mixed up with everything that exists in the heavens or on earth; which pervades every atom, rules the motions of animate and inanimate beings, and is as sensible in the descent of a rain-drop as in the falls of Niagara; in the weight of the air, as in the periods of the moon. Gravitation not only binds satellites to their planet, and planets to the sun, but it connects sun with sun throughout the wide extent of creation, and is the cause of the disturbances, as well as of the order of nature; since every tremor it excites in any one planet 2is immediately transmitted to the farthest limits of the system, in oscillations which correspond in their periods with the cause producing them, like sympathetic notes in music, or vibrations from the deep tones of an organ.
The heavens afford the most sublime subject of study which can be derived from science. The magnitude and splendour of the objects, the inconceivable rapidity with which they move, and the enormous distances between them, impress the mind with some notion of the energy that maintains them in their motions, with a durability to which we can see no limit. Equally conspicuous is the goodness of the great First Cause, in having endowed man with faculties, by which he can not only appreciate the magnificence of His works, but trace, with precision, the operation of His laws, use the globe he inhabits as a base wherewith to measure the magnitude and distance of the sun and planets, and make the diameter (Note 1) of the earth’s orbit the first step of a scale by which he may ascend to the starry firmament. Such pursuits, while they ennoble the mind, at the same time inculcate humility, by showing that there is a barrier which no energy, mental or physical, can ever enable us to pass: that, however profoundly we may penetrate the depths of space, there still remain innumerable systems, compared with which, those apparently so vast must dwindle into insignificance, or even become invisible; and that not only man, but the globe he inhabits—nay, the whole system of which it forms so small a part—might be annihilated, and its extinction be unperceived in the immensity of creation.
A complete acquaintance with physical astronomy can be attained by those only who are well versed in the higher branches of mathematical and mechanical science (N. 2), and they alone can appreciate the extreme beauty of the results, and of the means by which these results are obtained. It is nevertheless true, that a sufficient skill in analysis (N. 3) to follow the general outline—to see the mutual dependence of the different parts of the system, and to comprehend by what means the most extraordinary conclusions have been arrived at,—is within the reach of many who shrink from the task, appalled by difficulties, not more formidable than those incident to the study of the elements of every branch of knowledge. There is a wide distinction between the degree of mathematical acquirement necessary for 3making discoveries, and that which is requisite for understanding what others have done.
Our knowledge of external objects is founded upon experience, which furnishes facts; the comparison of these facts establishes relations, from which the belief that like causes will produce like effects leads to general laws. Thus, experience teaches that bodies fall at the surface of the earth with an accelerated velocity, and with a force proportional to their masses. By comparison, Newton proved that the force which occasions the fall of bodies at the earth’s surface is identical with that which retains the moon in her orbit; and he concluded, that, as the moon is kept in her orbit by the attraction of the earth, so the planets might be retained in their orbits by the attraction of the sun. By such steps he was led to the discovery of one of those powers with which the Creator has ordained that matter should reciprocally act upon matter.
Physical astronomy is the science which compares and identifies the laws of motion observed on earth with the motions that take place in the heavens: and which traces, by an uninterrupted chain of deduction from the great principle that governs the universe, the revolutions and rotations of the planets, and the oscillations (N. 4) of the fluids at their surfaces; and which estimates the changes the system has hitherto undergone, or may hereafter experience—changes which require millions of years for their accomplishment.
The accumulated efforts of astronomers, from the earliest dawn of civilization, have been necessary to establish the mechanical theory of astronomy. The courses of the planets have been observed for ages, with a degree of perseverance that is astonishing, if we consider the imperfection and even the want of instruments. The real motions of the earth have been separated from the apparent motions of the planets; the laws of the planetary revolutions have been discovered; and the discovery of these laws has led to the knowledge of the gravitation (N. 5) of matter. On the other hand, descending from the principle of gravitation, every motion in the solar system has been so completely explained, that the laws of any astronomical phenomena that may hereafter occur are already determined.
Attraction of a Sphere—Form of Celestial Bodies—Terrestrial Gravitation retains the Moon in her Orbit—The Heavenly Bodies move in Conic Sections—Gravitation Proportional to Mass—Gravitation of the Particles of Matter—Figure of the Planets—How it affects the Motions of their Satellites—Rotation and Translation impressed by the same Impulse—Motion of the Sun and Solar System.
It has been proved by Newton, that a particle of matter (N. 6) placed without the surface of a hollow sphere (N. 7) is attracted by it in the same manner as if the mass of the hollow sphere, or the whole matter it contains, were collected into one dense particle in its centre. The same is therefore true of a solid sphere, which may be supposed to consist of an infinite number of concentric hollow spheres (N. 8). This, however, is not the case with a spheroid (N. 9); but the celestial bodies are so nearly spherical, and at such remote distances from one another, that they attract and are attracted as if each were condensed into a single particle situate in its centre of gravity (N. 10)—a circumstance which greatly facilitates the investigation of their motions.
Newton has shown that the force which retains the moon in her orbit is the same with that which causes heavy substances to fall at the surface of the earth. If the earth were a sphere, and at rest, a body would be equally attracted, that is, it would have the same weight at every point of its surface, because the surface of a sphere is everywhere equally distant from its centre. But, as our planet is flattened at the poles (N. 11), and bulges at the equator, the weight of the same body gradually decreases from the poles, where it is greatest, to the equator, where it is least. There is, however, a certain mean (N. 12) latitude (N. 13), or part of the earth intermediate between the pole and the equator, where the attraction of the earth on bodies at its surface is the same as if it were a sphere; and experience shows that bodies there fall through 16·0697 feet in a second. The mean distance (N. 14) of the moon from the earth is about sixty times the mean radius (N. 15) of the earth. When the number 16·0697 is diminished 5in the ratio (N. 16) of 1 to 3600, which is the square of the moon’s distance (N. 17) from the earth’s centre, estimated in terrestrial radii, it is found to be exactly the space the moon would fall through in the first second of her descent to the earth, were she not prevented by the centrifugal force (N. 18) arising from the velocity with which she moves in her orbit. The moon is thus retained in her orbit by a force having the same origin, and regulated by the same law, with that which causes a stone to fall at the earth’s surface. The earth may, therefore, be regarded as the centre of a force which extends to the moon; and, as experience shows that the action and reaction of matter are equal and contrary (N. 19), the moon must attract the earth with an equal and contrary force.
Newton also ascertained that a body projected (N. 20) in space (N. 21) will move in a conic section (N. 22), if attracted by a force proceeding from a fixed point, with an intensity inversely as the square of the distance (N. 23); but that any deviation from that law will cause it to move in a curve of a different nature. Kepler found, by direct observation, that the planets describe ellipses (N. 24), or oval paths, round the sun. Later observations show that comets also move in conic sections. It consequently follows that the sun attracts all the planets and comets inversely as the square of their distances from its centre; the sun, therefore, is the centre of a force extending indefinitely in space, and including all the bodies of the system in its action.
Kepler also deduced from observation that the squares of the periodic times (N. 25) of the planets, or the times of their revolutions round the sun, are proportional to the cubes of their mean distances from its centre (N. 26). Hence the intensity of gravitation of all the bodies towards the sun is the same at equal distances. Consequently, gravitation is proportional to the masses (N. 27); for, if the planets and comets were at equal distances from the sun, and left to the effects of gravity, they would arrive at his surface at the same time (N. 28). The satellites also gravitate to their primaries (N. 29) according to the same law that their primaries do to the sun. Thus, by the law of action and reaction, each body is itself the centre of an attractive force extending indefinitely in space, causing all the mutual disturbances which render the celestial motions so complicated, and their investigation so difficult.
6The gravitation of matter directed to a centre, and attracting directly as the mass and inversely as the square of the distance, does not belong to it when considered in mass only; particle acts on particle according to the same law when at sensible distances from each other. If the sun acted on the centre of the earth, without attracting each of its particles, the tides would be very much greater than they now are, and would also, in other respects, be very different. The gravitation of the earth to the sun results from the gravitation of all its particles, which, in their turn, attract the sun in the ratio of their respective masses. There is a reciprocal action likewise between the earth and every particle at its surface. The earth and a feather mutually attract each other in the proportion of the mass of the earth to the mass of the feather. Were this not the case, and were any portion of the earth, however small, to attract another portion, and not be itself attracted, the centre of gravity of the earth would be moved in space by this action, which is impossible.
The forms of the planets result from the reciprocal attraction of their component particles. A detached fluid mass, if at rest, would assume the form of a sphere, from the reciprocal attraction of its particles. But if the mass revolve about an axis, it becomes flattened at the poles and bulges at the equator (N. 11), in consequence of the centrifugal force arising from the velocity of rotation (N. 30); for the centrifugal force diminishes the gravity of the particles at the equator, and equilibrium can only exist where these two forces are balanced by an increase of gravity. Therefore, as the attractive force is the same on all particles at equal distances from the centre of a sphere, the equatorial particles would recede from the centre, till their increase in number balance the centrifugal force by their attraction. Consequently, the sphere would become an oblate or flattened spheroid, and a fluid, partially or entirely covering a solid, as the ocean and atmosphere cover the earth, must assume that form in order to remain in equilibrio. The surface of the sea is, therefore, spheroidal, and the surface of the earth only deviates from that figure where it rises above or sinks below the level of the sea. But the deviation is so small, that it is unimportant when compared with the magnitude of the earth; for the mighty chain of the Andes, and the yet more lofty Himalaya, bear about the same proportion to the earth that a grain of sand does to a globe three feet in 7diameter. Such is the form of the earth and planets. The compression (N. 31) or flattening at their poles is, however, so small, that even Jupiter, whose rotation is the most rapid, and therefore the most elliptical of the planets, may, from his great distance, be regarded as spherical. Although the planets attract each other as if they were spheres, on account of their distances, yet the satellites (N. 32) are near enough to be sensibly affected in their motions by the forms of their primaries. The moon, for example, is so near the earth, that the reciprocal attraction between each of her particles, and each of the particles in the prominent mass at the terrestrial equator, occasions considerable disturbances in the motions of both bodies; for the action of the moon on the matter at the earth’s equator produces a nutation (N. 33) in the axis (N. 34) of rotation, and the reaction of that matter on the moon is the cause of a corresponding nutation in the lunar orbit (N. 35).
If a sphere at rest in space receive an impulse passing through its centre of gravity, all its parts will move with an equal velocity in a straight line; but, if the impulse does not pass through the centre of gravity, its particles, having unequal velocities, will have a rotatory or revolving motion, at the same time that it is translated (N. 36) in space. These motions are independent of one another; so that a contrary impulse, passing through its centre of gravity, will impede its progress, without interfering with its rotation. The sun rotates about an axis, and modern observations show that an impulse in a contrary direction has not been given to his centre of gravity, for he moves in space, accompanied by all those bodies which compose the solar system—a circumstance which in no way interferes with their relative motions; for, in consequence of the principle that force is proportional to velocity (N. 37), the reciprocal attractions of a system remain the same whether its centre of gravity be at rest, or moving uniformly in space. It is computed that, had the earth received its motion from a single impulse, that impulse must have passed through a point about twenty-five miles from its centre.
Since the motions of rotation and translation of the planets are independent of each other, though probably communicated by the same impulse, they form separate subjects of investigation.
Elliptical Motion—Mean and True Motion—Equinoctial—Ecliptic—Equinoxes—Mean and True Longitude—Equation of Centre—Inclination of the Orbits of Planets—Celestial Latitude—Nodes—Elements of an Orbit—Undisturbed or Elliptical Orbits—Great Inclination of the Orbits of the New Planets—Universal Gravitation the Cause of Perturbations in the Motions of the Heavenly Bodies—Problem of the Three Bodies—Stability of Solar System depends upon the Primitive Momentum of the Bodies.
A planet moves in its elliptical orbit with a velocity varying every instant, in consequence of two forces, one tending to the centre of the sun, and the other in the direction of a tangent (N. 38) to its orbit, arising from the primitive impulse given at the time when it was launched into space. Should the force in the tangent cease, the planet would fall to the sun by its gravity. Were the sun not to attract it, the planet would fly off in the tangent. Thus, when the planet is at the point of its orbit farthest from the sun, his action overcomes the planet’s velocity, and brings it towards him with such an accelerated motion, that at last it overcomes the sun’s attraction, and, shooting past him, gradually decreases in velocity until it arrives at the most distant point, where the sun’s attraction again prevails (N. 39). In this motion the radii vectores (N. 40), or imaginary lines joining the centres of the sun and the planets, pass over equal areas or spaces in equal times (N. 41).
The mean distance of a planet from the sun is equal to half the major axis (N. 42) of its orbit: if, therefore, the planet described a circle (N. 43) round the sun at its mean distance, the motion would be uniform, and the periodic time unaltered, because the planet would arrive at the extremities of the major axis at the same instant, and would have the same velocity, whether it moved in the circular or elliptical orbit, since the curves coincide in these points. But in every other part the elliptical, or true motion (N. 44), would either be faster or 9slower than the circular or mean motion (N. 45). As it is necessary to have some fixed point in the heavens from whence to estimate these motions, the vernal equinox (N. 46) at a given epoch has been chosen. The equinoctial, which is a great circle traced in the starry heavens by the imaginary extension of the plane of the terrestrial equator, is intersected by the ecliptic, or apparent path of the sun, in two points diametrically opposite to one another, called the vernal and autumnal equinoxes. The vernal equinox is the point through which the sun passes in going from the southern to the northern hemisphere; and the autumnal, that in which he crosses from the northern to the southern. The mean or circular motion of a body, estimated from the vernal equinox, is its mean longitude; and its elliptical, or true motion, reckoned from that point, is its true longitude (N. 47): both being estimated from west to east, the direction in which the bodies move. The difference between the two is called the equation of the centre (N. 48); which consequently vanishes at the apsides (N. 49), or extremities of the major axis, and is at its maximum ninety degrees (N. 50) distant from these points, or in quadratures (N. 51), where it measures the excentricity (N. 52) of the orbit; so that the place of the planet in its elliptical orbit is obtained by adding or subtracting the equation of the centre to or from its mean longitude.
The orbits of the principal planets have a very small obliquity or inclination (N. 53) to the plane of the ecliptic in which the earth moves; and, on that account, astronomers refer their motions to this plane at a given epoch as a known and fixed position. The angular distance of a planet from the plane of the ecliptic is its latitude (N. 54), which is south or north according as the planet is south or north of that plane. When the planet is in the plane of the ecliptic, its latitude is zero; it is then said to be in its nodes (N. 55). The ascending node is that point in the ecliptic through which the planet passes in going from the southern to the northern hemisphere. The descending node is a corresponding point in the plane of the ecliptic diametrically opposite to the other, through which the planet descends in going from the northern to the southern hemisphere. The longitude and latitude of a planet cannot be obtained by direct observation, but are deduced from observations made at the surface of the 10earth by a very simple computation. These two quantities, however, will not give the place of a planet in space. Its distance from the sun (N. 56) must also be known; and, for the complete determination of its elliptical motion, the nature and position of its orbit must be ascertained by observation. This depends upon seven quantities, called the elements of the orbit (N. 57). These are, the length of the major axis, and the excentricity, which determine the form of the orbit; the longitude of the planet when at its least distance from the sun, called the longitude of the perihelion; the inclination of the orbit to the plane of the ecliptic, and the longitude of its ascending node: these give the position of the orbit in space; but the periodic time, and the longitude of the planet at a given instant, called the longitude of the epoch, are necessary for finding the place of the body in its orbit at all times. A perfect knowledge of these seven elements is requisite for ascertaining all the circumstances of undisturbed elliptical motion. By such means it is found that the paths of the planets, when their mutual disturbances are omitted, are ellipses nearly approaching to circles, whose planes, slightly inclined to the ecliptic, cut it in straight lines, passing through the centre of the sun (N. 58). The orbits of the recently-discovered planets deviate more from the ecliptic than those of the ancient planets: that of Pallas, for instance, has an inclination of 34° 42ʹ 29·8ʺ to it; on which account it is more difficult to determine their motions.
Were the planets attracted by the sun only, they would always move in ellipses, invariable in form and position; and because his action is proportional to his mass, which is much larger than that of all the planets put together, the elliptical is the nearest approximation to their true motions. The true motions of the planets are extremely complicated, in consequence of their mutual attraction, so that they do not move in any known or symmetrical curve, but in paths now approaching to, now receding from, the elliptical form; and their radii vectores do not describe areas or spaces exactly proportional to the time, so that the areas become a test of disturbing forces.
To determine the motion of each body, when disturbed by all the rest, is beyond the power of analysis. It is therefore necessary to estimate the disturbing action of one planet at a time, 11whence the celebrated problem of the three bodies, originally applied to the moon, the earth, and the sun—namely, the masses being given of three bodies projected from three given points, with velocities given both in quantity and direction; and supposing the bodies to gravitate to one another with forces that are directly as their masses, and inversely as the squares of the distances, to find the lines described by these bodies, and their positions at any given instant; or, in other words, to determine the path of a celestial body when attracted by a second body, and disturbed in its motion round the second body by a third—a problem equally applicable to planets, satellites, and comets.
By this problem the motions of translation of the celestial bodies are determined. It is an extremely difficult one, and would be infinitely more so if the disturbing action were not very small when compared with the central force; that is, if the action of the planets on one another were not very small when compared with that of the sun. As the disturbing influence of each body may be found separately, it is assumed that the action of the whole system, in disturbing any one planet, is equal to the sum of all the particular disturbances it experiences, on the general mechanical principle, that the sum of any number of small oscillations is nearly equal to their simultaneous and joint effect.
On account of the reciprocal action of matter, the stability of the system depends upon the intensity of the primitive momentum (N. 59) of the planets, and the ratio of their masses to that of the sun; for the nature of the conic sections in which the celestial bodies move depends upon the velocity with which they were first propelled in space. Had that velocity been such as to make the planets move in orbits of unstable equilibrium (N. 60), their mutual attractions might have changed them into parabolas, or even hyperbolas (N. 22); so that the earth and planets might, ages ago, have been sweeping far from our sun through the abyss of space. But as the orbits differ very little from circles, the momentum of the planets, when projected, must have been exactly sufficient to ensure the permanency and stability of the system. Besides, the mass of the sun is vastly greater than that of any planet; and as their inequalities bear the same ratio to their elliptical motions that their masses do to that of the sun, their 12mutual disturbances only increase or diminish the excentricities of their orbits by very minute quantities; consequently the magnitude of the sun’s mass is the principal cause of the stability of the system. There is not in the physical world a more splendid example of the adaptation of means to the accomplishment of an end than is exhibited in the nice adjustment of these forces, at once the cause of the variety and of the order of Nature.
Perturbations, Periodic and Secular—Disturbing Action equivalent to three Partial Forces—Tangential Force the cause of the Periodic Inequalities in Longitude, and Secular Inequalities in the Form and Position of the Orbit in its own Plane—Radial Force the cause of Variations in the Planet’s Distance from the Sun—It combines with the Tangential Force to produce the Secular Variations in the Form and Position of the Orbit in its own Plane—Perpendicular Force the cause of Periodic Perturbations in Latitude, and Secular Variations in the Position of the Orbit with regard to the Plane of the Ecliptic—Mean Motion and Major Axis Invariable—Stability of System—Effects of a Resisting Medium—Invariable Plane of the Solar System and of the Universe—Great Inequality of Jupiter and Saturn.
The planets are subject to disturbances of two kinds, both resulting from the constant operation of their reciprocal attraction: one kind, depending upon their positions with regard to each other, begins from zero, increases to a maximum, decreases, and becomes zero again, when the planets return to the same relative positions. In consequence of these, the disturbed planet is sometimes drawn away from the sun, sometimes brought nearer to him: sometimes it is accelerated in its motion, and sometimes retarded. At one time it is drawn above the plane of its orbit, at another time below it, according to the position of the disturbing body. All such changes, being accomplished in short periods, some in a few months, others in years, or in hundreds of years, are denominated periodic inequalities. The inequalities of the other kind, though occasioned likewise by the disturbing energy of the planets, are entirely independent of their relative positions. They depend upon the relative positions of the orbits alone, whose forms and places in space are altered by very minute quantities, in immense periods of time, and are therefore called secular inequalities.
The periodical perturbations are compensated when the bodies return to the same relative positions with regard to one another and to the sun: the secular inequalities are compensated when 14the orbits return to the same positions relatively to one another and to the plane of the ecliptic.
Planetary motion, including both these kinds of disturbance, may be represented by a body revolving in an ellipse, and making small and transient deviations, now on one side of its path, and now on the other, whilst the ellipse itself is slowly, but perpetually, changing both in form and position.
The periodic inequalities are merely transient deviations of a planet from its path, the most remarkable of which only lasts about 918 years; but, in consequence of the secular disturbances, the apsides, or extremities of the major axes of all the orbits, have a direct but variable motion in space, excepting those of the orbit of Venus, which are retrograde (N. 61), and the lines of the nodes move with a variable velocity in a contrary direction. Besides these, the inclination and excentricity of every orbit are in a state of perpetual but slow change. These effects result from the disturbing action of all the planets on each. But, as it is only necessary to estimate the disturbing influence of one body at a time, what follows may convey some idea of the manner in which one planet disturbs the elliptical motion of another.
Suppose two planets moving in ellipses round the sun; if one of them attracted the other and the sun with equal intensity, and in parallel directions (N. 62), it would have no effect in disturbing the elliptical motion. The inequality of this attraction is the sole cause of perturbation, and the difference between the disturbing planet’s action on the sun and on the disturbed planet constitutes the disturbing force, which consequently varies in intensity and direction with every change in the relative positions of the three bodies. Although both the sun and planet are under the influence of the disturbing force, the motion of the disturbed planet is referred to the centre of the sun as a fixed point, for convenience. The whole force (N. 63) which disturbs a planet is equivalent to three partial forces. One of these acts on the disturbed planet, in the direction of a tangent to its orbit, and is called the tangential force: it occasions secular inequalities in the form and position of the orbit in its own plane, and is the sole cause of the periodical perturbations in the planet’s longitude. Another acts upon the same body in the direction of its radius vector, that is, in the line joining the centres of 15the sun and planet, and is called the radial force: it produces periodical changes in the distance of the planet from the sun, and affects the form and position of the orbit in its own plane. The third, which may be called the perpendicular force, acts at right angles to the plane of the orbit, occasions the periodic inequalities in the planet’s latitude, and affects the position of the orbit with regard to the plane of the ecliptic.
It has been observed, that the radius vector of a planet, moving in a perfectly elliptical orbit, passes over equal spaces or areas in equal times; a circumstance which is independent of the law of the force, and would be the same whether it varied inversely as the square of the distance, or not, provided only that it be directed to the centre of the sun. Hence the tangential force, not being directed to the centre, occasions an unequable description of areas, or, what is the same thing, it disturbs the motion of the planet in longitude. The tangential force sometimes accelerates the planet’s motion, sometimes retards it, and occasionally has no effect at all. Were the orbits of both planets circular, a complete compensation would take place at each revolution of the two planets, because the arcs in which the accelerations and retardations take place would be symmetrical on each side of the disturbing force. For it is clear, that if the motion be accelerated through a certain space, and then retarded through as much, the motion at the end of the time will be the same as if no change had taken place. But, as the orbits of the planets are ellipses, this symmetry does not hold: for, as the planet moves unequably in its orbit, it is in some positions more directly, and for a longer time, under the influence of the disturbing force than in others. And, although multitudes of variations do compensate each other in short periods, there are others, depending on peculiar relations among the periodic times of the planets, which do not compensate each other till after one, or even till after many revolutions of both bodies. A periodical inequality of this kind in the motions of Jupiter and Saturn has a period of no less than 918 years.
The radial force, or that part of the disturbing force which acts in the direction of the line joining the centres of the sun and disturbed planet, has no effect on the areas, but is the cause of periodical changes of small extent in the distance of the planet from the sun. It has already been shown, that the force producing 16perfectly elliptical motion varies inversely as the square of the distance, and that a force following any other law would cause the body to move in a curve of a very different kind. Now, the radial disturbing force varies directly as the distance; and, as it sometimes combines with and increases the intensity of the sun’s attraction for the disturbed body, and at other times opposes and consequently diminishes it, in both cases it causes the sun’s attraction to deviate from the exact law of gravity, and the whole action of this compound central force on the disturbed body is either greater or less than what is requisite for perfectly elliptical motion. When greater, the curvature of the disturbed planet’s path, on leaving its perihelion (N. 64), or point nearest the sun, is greater than it would be in the ellipse, which brings the planet to its aphelion (N. 65), or point farthest from the sun, before it has passed through 180°, as it would do if undisturbed. So that in this case the apsides, or extremities of the major axis, advance in space. When the central force is less than the law of gravity requires, the curvature of the planet’s path is less than the curvature of the ellipse. So that the planet, on leaving its perihelion, would pass through more than 180° before arriving at its aphelion, which causes the apsides to recede in space (N. 66). Cases both of advance and recess occur during a revolution of the two planets; but those in which the apsides advance preponderate. This, however, is not the full amount of the motion of the apsides; part arises also from the tangential force (N. 63), which alternately accelerates and retards the velocity of the disturbed planet. An increase in the planet’s tangential velocity diminishes the curvature of its orbit, and is equivalent to a decrease of central force. On the contrary, a decrease of the tangential velocity, which increases the curvature of the orbit, is equivalent to an increase of central force. These fluctuations, owing to the tangential force, occasion an alternate recess and advance of the apsides, after the manner already explained (N. 66). An uncompensated portion of the direct motion, arising from this cause, conspires with that already impressed by the radial force, and in some cases even nearly doubles the direct motion of these points. The motion of the apsides may be represented by supposing a planet to move in an ellipse, while the ellipse itself is slowly revolving about the sun in the same plane (N. 67). This motion of the major axis, 17which is direct in all the orbits except that of the planet Venus, is irregular, and so slow that it requires more than 109,830 years for the major axis of the earth’s orbit to accomplish a sidereal revolution (N. 68), that is, to return to the same stars; and 20,984 years to complete its tropical revolution (N. 69), or to return to the same equinox. The difference between these two periods arises from a retrograde motion in the equinoctial point, which meets the advancing axis before it has completed its revolution with regard to the stars. The major axis of Jupiter’s orbit requires no less than 200,610 years to perform its sidereal revolution, and 22,748 years to accomplish its tropical revolution from the disturbing action of Saturn alone.
A variation in the excentricity of the disturbed planet’s orbit is an immediate consequence of the deviation from elliptical curvature, caused by the action of the disturbing force. When the path of the body, in proceeding from its perihelion to its aphelion, is more curved than it ought to be from the effect of the disturbing forces, it falls within the elliptical orbit, the excentricity is diminished, and the orbit becomes more nearly circular; when that curvature is less than it ought to be, the path of the planet falls without its elliptical orbit (N. 66), and the excentricity is increased; during these changes, the length of the major axis is not altered, the orbit only bulges out, or becomes more flat (N. 70). Thus the variation in the excentricity arises from the same cause that occasions the motion of the apsides (N. 67). There is an inseparable connection between these two elements: they vary simultaneously, and have the same period; so that, whilst the major axis revolves in an immense period of time, the excentricity increases and decreases by very small quantities, and at length returns to its original magnitude at each revolution of the apsides. The terrestrial excentricity is decreasing at the rate of about 40 miles annually; and, if it were to decrease equably, it would be 39,861 years before the earth’s orbit became a circle. The mutual action of Jupiter and Saturn occasions variations in the excentricity of both orbits, the greatest excentricity of Jupiter’s orbit corresponding to the least of Saturn’s. The period in which these vicissitudes are accomplished is 70,414 years, estimating the action of these two planets alone; but, if the action of all the planets were estimated, the cycle would extend to millions of years.
18That part of the disturbing force is now to be considered which acts perpendicularly to the plane of the orbit, causing periodic perturbations in latitude, secular variations in the inclination of the orbit, and a retrograde motion to its nodes on the true plane of the ecliptic (N. 71). This force tends to pull the disturbed body above, or push (N. 72) it below, the plane of its orbit, according to the relative positions of the two planets with regard to the sun, considered to be fixed. By this action, it sometimes makes the plane of the orbit of the disturbed body tend to coincide with the plane of the ecliptic, and sometimes increases its inclination to that plane. In consequence of which, its nodes alternately recede or advance on the ecliptic (N. 73). When the disturbing planet is in the line of the disturbed planet’s nodes (N. 74), it neither affects these points, the latitude, nor the inclination, because both planets are then in the same plane. When it is at right angles to the line of the nodes, and the orbit symmetrical on each side of the disturbing force, the average motion of these points, after a revolution of the disturbed body, is retrograde, and comparatively rapid: but, when the disturbing planet is so situated that the orbit of the disturbed planet is not symmetrical on each side of the disturbing force, which is most frequently the case, every possible variety of action takes place. Consequently, the nodes are perpetually advancing or receding with unequal velocity; but, as a compensation is not effected, their motion is, on the whole, retrograde.
With regard to the variations in the inclination, it is clear, that, when the orbit is symmetrical on each side of the disturbing force, all its variations are compensated after a revolution of the disturbed body, and are merely periodical perturbations in the planet’s latitude; and no secular change is induced in the inclination of the orbit. When, on the contrary, that orbit is not symmetrical on each side of the disturbing force, although many of the variations in latitude are transient or periodical, still, after a complete revolution of the disturbed body, a portion remains uncompensated, which forms a secular change in the inclination of the orbit to the plane of the ecliptic. It is true, part of this secular change in the inclination is compensated by the revolution of the disturbing body, whose motion has not hitherto been taken into the account, so that perturbation compensates perturbation; but still a comparatively permanent 19change is effected in the inclination, which is not compensated till the nodes have accomplished a complete revolution.
The changes in the inclination are extremely minute (N. 75), compared with the motion of the nodes, and there is the same kind of inseparable connection between their secular changes that there is between the variation of the excentricity and the motion of the major axis. The nodes and inclinations vary simultaneously; their periods are the same, and very great. The nodes of Jupiter’s orbit, from the action of Saturn alone, require 36,261 years to accomplish even a tropical revolution. In what precedes, the influence of only one disturbing body has been considered; but, when the action and reaction of the whole system are taken into account, every planet is acted upon, and does itself act, in this manner, on all the others; and the joint effect keeps the inclinations and excentricities in a state of perpetual variation. It makes the major axes of all the orbits continually revolve, and causes, on an average, a retrograde motion of the nodes of each orbit upon every other. The ecliptic (N. 71) itself is in motion from the mutual action of the earth and planets, so that the whole is a compound phenomenon of great complexity, extending through unknown ages. At the present time the inclinations of all the orbits are decreasing, but so slowly, that the inclination of Jupiter’s orbit is only about six minutes less than it was in the age of Ptolemy.
But, in the midst of all these vicissitudes, the length of the major axes and the mean motions of the planets remain permanently independent of secular changes. They are so connected by Kepler’s law, of the squares of the periodic times being proportional to the cubes of the mean distances of the planets from the sun, that one cannot vary without affecting the other. And it is proved, that any variations which do take place are transient, and depend only on the relative positions of the bodies.
It is true that, according to theory, the radial disturbing force should permanently alter the dimensions of all the orbits, and the periodic times of all the planets, to a certain degree. For example, the masses of all the planets revolving within the orbit of any one, such as Mars, by adding to the interior mass, increase the attracting force of the sun, which, therefore, must contract the dimensions of the orbit of that planet, and diminish its periodic time; whilst the planets exterior to Mars’s orbit must 20have the contrary effect. But the mass of the whole of the planets and satellites taken together is so small, when compared with that of the sun, that these effects are quite insensible, and could only have been discovered by theory. And, as it is certain that the length of the major axes and the mean motions are not permanently changed by any other power whatever, it may be concluded that they are invariable.
With the exception of these two elements, it appears that all the bodies are in motion, and every orbit in a state of perpetual change. Minute as these changes are, they might be supposed to accumulate in the course of ages, sufficiently to derange the whole order of nature, to alter the relative positions of the planets, to put an end to the vicissitudes of the seasons, and to bring about collisions which would involve our whole system, now so harmonious, in chaotic confusion. It is natural to inquire, what proof exists that nature will be preserved from such a catastrophe? Nothing can be known from observation, since the existence of the human race has occupied comparatively but a point in duration, while these vicissitudes embrace myriads of ages. The proof is simple and conclusive. All the variations of the solar system, secular as well as periodic, are expressed analytically by the sines and cosines of circular arcs (N. 76), which increase with the time; and, as a sine or cosine can never exceed the radius, but must oscillate between zero and unity, however much the time may increase, it follows that when the variations have accumulated to a maximum by slow changes, in however long a time, they decrease, by the same slow degrees, till they arrive at their smallest value, again to begin a new course; thus for ever oscillating about a mean value. This circumstance, however, would be insufficient, were it not for the small excentricities of the planetary orbits, their minute inclinations to the plane of the ecliptic, and the revolutions of all the bodies, as well planets as satellites, in the same direction. These secure the perpetual stability of the solar system (N. 77). However, at the time that the stability was proved by La Grange and La Place, the telescopic planets between Mars and Jupiter had not been discovered; but La Grange, having investigated the subject under a very general point of view, showed that, if a planetary system be composed of very unequal masses, the whole of the larger would maintain an unalterable stability with regard to the form and 21position of their orbits, while the orbits of the lesser might undergo unlimited changes. M. Le Verrier has applied this to the solar system, and has found that the orbits of all the larger planets will for ever maintain an unalterable stability in form and position; for, though liable to mutations of very long periods, they return again exactly to what they originally were, oscillating between very narrow limits; but he found a zone of instability between the orbit of Mars, and twice the mean distance of the earth from the sun,[1] or between 1·5 and 2·00; therefore the position and form of the orbits of such of the telescopic planets as revolve within that zone will be subject to unlimited variations. But the orbits of those more remote from the sun than Flora, or beyond 2·20, will be stable, so that their excentricities and inclinations must always have been, and will always remain, very great, since they must have depended upon the primitive conditions that prevailed when these planetary atoms were launched into space. The 51st of these small bodies, which was discovered, and the elements of its orbit determined, by M. Valz, at Nimes, has a mean distance of 1·88; so it revolves within the zone of instability. It has a shorter periodic time than any of those previously discovered, and a greater excentricity, with the exception of Nysa. Its orbit cuts that of Mars, and comes nearer to the earth than the orbits of either Mars or Venus, a circumstance which would be favourable for correcting the parallax of the sun, or confirming its accuracy. The telescopic planets, numerous as they are, have no influence on the motions of the larger planets, for Jupiter has a diameter of 90,734 miles, while that of Pallas, his nearest neighbour, is only 97 miles, little more than the distance from London to Bath. The diameter of Mars, on the other side of the small planets, is 4546 miles, and that of the earth 79251⁄2 miles, so that the telescopic group are too minute to disturb the others. M. Le Verrier found another zone of instability between Venus and the sun, on the border of which Mercury is revolving, the inclination of whose orbit to the plane of the ecliptic is about 7°, which is more than that of any of the large planets. Neptune’s 22orbit is, no doubt, as stable as that of any other of the large planets, as the inclination is very small, but he will have periodical variations of very long duration from the reciprocal attraction between him and Uranus, one especially of an enormous duration, similar to those of Jupiter and Saturn, and, like them, depending on the time of his revolution round the sun, being nearly twice as long as that of Saturn. Mr. Adams has computed that Neptune produces a periodical perturbation in the motion of Uranus, whose duration is about 6800 years.
The equilibrium of the system, however, would be deranged if the planets moved in a resisting medium (N. 78) sufficiently dense to diminish their tangential velocity, for then both the excentricities and the major axes of the orbits would vary with the time, so that the stability of the system would be ultimately destroyed. The existence of an ethereal medium is now proved; and, although it is so extremely rare that hitherto its effects on the motions of the planets have been altogether insensible, there can be no doubt that, in the immensity of time, it will modify the forms of the planetary orbits, and may at last even cause the destruction of our system, which in itself contains no principle of decay, unless a rotatory motion from west to east has been given to this medium by the bodies of the solar system, which have all been revolving about the sun in that direction for unknown ages. This rotation, which seems to be highly probable, may even have been coeval with its creation. Such a vortex would have no effect on bodies moving with it, but it would influence the motions of those revolving in a contrary direction. It is possible that the disturbances experienced by comets, which have already revealed the existence of this medium, may also, in time, disclose its rotatory motion.
The form and position of the planetary orbits, and the motion of the bodies in the same direction, together with the periodicity of the terms in which the inequalities are expressed, assure us that the variations of the system are confined within very narrow limits, and that, although we do not know the extent of the limits, nor the period of that grand cycle which probably embraces millions of years, yet they never will exceed what is requisite for the stability and harmony of the whole; for the preservation of which every circumstance is so beautifully and wonderfully adapted.
23The plane of the ecliptic itself, though assumed to be fixed at a given epoch for the convenience of astronomical computation, is subject to a minute secular variation of 45ʺ·7, occasioned by the reciprocal action of the planets. But, as this is also periodical, and cannot exceed 2° 42ʹ, the terrestrial equator, which is inclined to it at an angle[2] of 23° 27ʹ 28ʺ·29, will never coincide with the plane of the ecliptic: so there never can be perpetual spring (N. 79). The rotation of the earth is uniform; therefore day and night, summer and winter, will continue their vicissitudes while the system endures, or is undisturbed by foreign causes.
The stability of our system was established by La Grange: “a discovery,” says Professor Playfair, “that must render the name for ever memorable in science, and revered by those who delight in the contemplation of whatever is excellent and sublime.” After Newton’s discovery of the mechanical laws of the elliptical orbits of the planets, that of their periodical inequalities, by La Grange, is, without doubt, the noblest truth in the mechanism of the heavens; and, in respect of the doctrine of final causes, it may be regarded as the greatest of all.
Notwithstanding the permanency of our system, the secular variations in the planetary orbits would have been extremely embarrassing to astronomers when it became necessary to compare observations separated by long periods. The difficulty was in part obviated, and the principle for accomplishing it established, by La Place, and has since been extended by M. Poinsot. It appears that there exists an invariable plane (N. 80), passing through the centre of gravity of the system, about which the whole oscillates within very narrow limits, and that this plane will always remain parallel to itself, whatever changes time may induce in the orbits of the planets, in the plane of the ecliptic, or even in the law of gravitation; provided only that our system remains unconnected with any other. The position of the plane is determined by this property—that, if each particle in the system be multiplied by the area described upon this plane in a 24given time, by the projection of its radius vector about the common centre of gravity of the whole, the sum of all these products will be a maximum (N. 81). La Place found that the plane in question is inclined to the ecliptic at an angle of nearly 1° 34ʹ 15ʺ, and that, in passing through the sun, and about midway between the orbits of Jupiter and Saturn, it may be regarded as the equator of the solar system, dividing it into two parts, which balance one another in all their motions. This plane of greatest inertia, by no means peculiar to the solar system, but existing in every system of bodies submitted to their mutual attractions only, always maintains a fixed position, whence the oscillations of the system may be estimated through unlimited time. Future astronomers will know, from its immutability or variation, whether the sun and his attendants are connected or not with the other systems of the universe. Should there be no link between them, it may be inferred, from the rotation of the sun, that the centre of gravity (N. 82) of the system situate within his mass describes a straight line in this invariable plane or great equator of the solar system, which, unaffected by the changes of time, will maintain its stability through endless ages. But, if the fixed stars, comets, or any unknown and unseen bodies, affect our sun and planets, the nodes of this plane will slowly recede on the plane of that immense orbit which the sun may describe about some most distant centre, in a period which it transcends the power of man to determine. There is every reason to believe that this is the case; for it is more than probable that, remote as the fixed stars are, they in some degree influence our system, and that even the invariability of this plane is relative, only appearing fixed to creatures incapable of estimating its minute and slow changes during the small extent of time and space granted to the human race. “The development of such changes,” as M. Poinsot justly observes, “is similar to an enormous curve, of which we see so small an arc that we imagine it to be a straight line.” If we raise our views to the whole extent of the universe, and consider the stars, together with the sun, to be wandering bodies, revolving about the common centre of creation, we may then recognise in the equatorial plane passing through the centre of gravity of the universe the only instance of absolute and eternal repose.
All the periodic and secular inequalities deduced from the law 25of gravitation are so perfectly confirmed by observation, that analysis has become one of the most certain means of discovering the planetary irregularities, either when they are too small, or too long in their periods, to be detected by other methods. Jupiter and Saturn, however, exhibit inequalities which for a long time seemed discordant with that law. All observations, from those of the Chinese and Arabs down to the present day, prove that for ages the mean motions of Jupiter and Saturn have been affected by a great inequality of a very long period, forming an apparent anomaly in the theory of the planets. It was long known by observation that five times the mean motion of Saturn is nearly equal to twice that of Jupiter; a relation which the sagacity of La Place perceived to be the cause of a periodic irregularity in the mean motion of each of these planets, which completes its period in nearly 918 years, the one being retarded while the other is accelerated; but both the magnitude and period of these quantities vary, in consequence of the secular variations in the elements of the orbits. Suppose the two planets to be on the same side of the sun, and all three in the same straight line, they are then said to be in conjunction (N. 83). Now, if they begin to move at the same time, one making exactly five revolutions in its orbit while the other only accomplishes two, it is clear that Saturn, the slow-moving body, will only have got through a part of its orbit during the time that Jupiter has made one whole revolution and part of another, before they be again in conjunction. It is found that during this time their mutual action is such as to produce a great many perturbations which compensate each other, but that there still remains a portion outstanding, owing to the length of time during which the forces act in the same manner; and, if the conjunction always happened in the same point of the orbit, this uncompensated inequality in the mean motion would go on increasing till the periodic times and forms of the orbits were completely and permanently changed: a case that would actually take place if Jupiter accomplished exactly five revolutions in the time Saturn performed two. These revolutions are, however, not exactly commensurable; the points in which the conjunctions take place are in advance each time as much as 8°·37; so that the conjunctions do not happen exactly in the same points of the orbits till after a period of 850 years; and, in consequence of this small advance, 26the planets are brought into such relative positions, that the inequality, which seemed to threaten the stability of the system, is completely compensated, and the bodies, having returned to the same relative positions with regard to one another and the sun, begin a new course. The secular variations in the elements of the orbit increase the period of the inequality to 918 years (N. 84). As any perturbation which affects the mean motion affects also the major axis, the disturbing forces tend to diminish the major axis of Jupiter’s orbit, and increase that of Saturn’s, during one half of the period, and the contrary during the other half. This inequality is strictly periodical, since it depends upon the configuration (N. 85) of the two planets; and theory is confirmed by observation, which shows that, in the course of twenty centuries, Jupiter’s mean motion has been accelerated by about 3° 23ʹ, and Saturn’s retarded by 5° 13ʹ. Several instances of perturbations of this kind occur in the solar system. One, in the mean motions of the Earth and Venus, only amounting to a few seconds, has been recently worked out with immense labour by Professor Airy. It accomplishes its changes in 240 years, and arises from the circumstance of thirteen times the periodic time of Venus being nearly equal to eight times that of the Earth. Small as it is, it is sensible in the motions of the Earth.
It might be imagined that the reciprocal action of such planets as have satellites would be different from the influence of those that have none. But the distances of the satellites from their primaries are incomparably less than the distances of the planets from the sun, and from one another. So that the system of a planet and its satellites moves nearly as if all these bodies were united in their common centre of gravity. The action of the sun, however, in some degree disturbs the motion of the satellites about their primary.
Theory of Jupiter’s Satellites—Effects of the Figure of Jupiter upon his Satellites—Position of their Orbits—Singular Laws among the Motions of the first Three Satellites—Eclipses of the Satellites—Velocity of Light—Aberration—Ethereal Medium—Satellites of Saturn and Uranus.
The changes which take place in the planetary system are exhibited on a smaller scale by Jupiter and his satellites; and, as the period requisite for the development of the inequalities of these moons only extends to a few centuries, it may be regarded as an epitome of that grand cycle which will not be accomplished by the planets in myriads of ages. The revolutions of the satellites about Jupiter are precisely similar to those of the planets about the sun; it is true they are disturbed by the sun, but his distance is so great, that their motions are nearly the same as if they were not under his influence. The satellites, like the planets, were probably projected in elliptical orbits: but, as the masses of the satellites are nearly 100,000 times less than that of Jupiter; and as the compression of Jupiter’s spheroid is so great, in consequence of his rapid rotation, that his equatorial diameter exceeds his polar diameter by no less than 6000 miles; the immense quantity of prominent matter at his equator must soon have given the circular form observed in the orbits of the first and second satellites, which its superior attraction will always maintain. The third and fourth satellites, being farther removed from its influence, revolve in orbits with a very small excentricity. And, although the first two sensibly move in circles, their orbits acquire a small ellipticity, from the disturbances they experience (N. 86).
It has been stated, that the attraction of a sphere on an exterior body is the same as if its mass were united in one particle in its centre of gravity, and therefore inversely as the square of the distance. In a spheroid, however, there is an additional force arising from the bulging mass at its equator, which, not following the exact law of gravity, acts as a disturbing force. 28One effect of this disturbing force in the spheroid of Jupiter is to occasion a direct motion in the greater axes of the orbits of all his satellites, which is more rapid the nearer the satellite is to the planet, and very much greater than that part of their motion which arises from the disturbing action of the sun. The same cause occasions the orbits of the satellites to remain nearly in the plane of Jupiter’s equator (N. 87), on account of which the satellites are always seen nearly in the same line (N. 88); and the powerful action of that quantity of prominent matter is the reason why the motions of the nodes of these small bodies are so much more rapid than those of the planet. The nodes of the fourth satellite accomplish a tropical revolution in 531 years, while those of Jupiter’s orbit require no less than 36,261 years;—a proof of the reciprocal attraction between each particle of Jupiter’s equator and of the satellites. In fact, if the satellites moved exactly in the plane of Jupiter’s equator, they would not be pulled out of that plane, because his attraction would be equal on both sides of it. But, as their orbits have a small inclination to the plane of the planet’s equator, there is a want of symmetry, and the action of the protuberant matter tends to make the nodes regress by pulling the satellites above or below the planes of their orbits; an action which is so great on the interior satellites, that the motions of their nodes are nearly the same as if no other disturbing force existed.
The orbits of the satellites do not retain a permanent inclination, either to the plane of Jupiter’s equator, or to that of his orbit, but to certain planes passing between the two, and through their intersection. These have a greater inclination to his equator the farther the satellite is removed, owing to the influence of Jupiter’s compression; and they have a slow motion corresponding to secular variations in the planes of Jupiter’s orbit and equator.
The satellites are not only subject to periodic and secular inequalities from their mutual attraction, similar to those which affect the motions and orbits of the planets, but also to others peculiar to themselves. Of the periodic inequalities arising from their mutual attraction the most remarkable take place in the angular motions (N. 89) of the three nearest to Jupiter, the second of which receives from the first a perturbation similar to that which it produces in the third; and it experiences from the 29third a perturbation similar to that which it communicates to the first. In the eclipses these two inequalities are combined into one, whose period is 437·659 days. The variations peculiar to the satellites arise from the secular inequalities occasioned by the action of the planets in the form and position of Jupiter’s orbit, and from the displacement of his equator. It is obvious that whatever alters the relative positions of the sun, Jupiter, and his satellites, must occasion a change in the directions and intensities of the forces, which will affect the motions and orbits of the satellites. For this reason the secular variations in the excentricity of Jupiter’s orbit occasion secular inequalities in the mean motions of the satellites, and in the motions of the nodes and apsides of their orbits. The displacement of the orbit of Jupiter, and the variation in the position of his equator, also affect these small bodies (N. 90). The plane of Jupiter’s equator is inclined to the plane of his orbit at an angle of 3° 5ʹ 30ʺ, so that the action of the sun and of the satellites themselves produces a nutation and precession (N. 91) in his equator, precisely similar to that which takes place in the rotation of the earth, from the action of the sun and moon. Hence the protuberant matter at Jupiter’s equator is continually changing its position with regard to the satellites, and produces corresponding mutations in their motions. And, as the cause must be proportional to the effect, these inequalities afford the means, not only of ascertaining the compression of Jupiter’s spheroid, but they prove that his mass is not homogeneous. Although the apparent diameters of the satellites are too small to be measured, yet their perturbations give the values of their masses with considerable accuracy—a striking proof of the power of analysis.
A singular law obtains among the mean motions and mean longitudes of the first three satellites. It appears from observation that the mean motion of the first satellite, plus twice that of the third, is equal to three times that of the second; and that the mean longitude of the first satellite, minus three times that of the second, plus twice that of the third, is always equal to two right angles. It is proved by theory, that, if these relations had only been approximate when the satellites were first launched into space, their mutual attractions would have established and maintained them, notwithstanding the secular inequalities to which they are liable. They extend to the synodic motions 30(N. 92) of the satellites; consequently they affect their eclipses, and have a very great influence on their whole theory. The satellites move so nearly in the plane of Jupiter’s equator, which has a very small inclination to his orbit, that the first three are eclipsed at each revolution by the shadow of the planet, which is much larger than the shadow of the moon: the fourth satellite is not eclipsed so frequently as the others. The eclipses take place close to the disc of Jupiter when he is near opposition (N. 93); but at times his shadow is so projected with regard to the earth, that the third and fourth satellites vanish and reappear on the same side of the disc (N. 94). These eclipses are in all respects similar to those of the moon: but, occasionally, the satellites eclipse Jupiter, sometimes passing like obscure spots across his surface, resembling annular eclipses of the sun, and sometimes like a bright spot traversing one of his dark belts. Before opposition, the shadow of the satellite, like a round black spot, precedes its passage over the disc of the planet; and, after opposition, the shadow follows the satellite.
In consequence of the relations already mentioned in the mean motions and mean longitudes of the first three satellites, they never can be all eclipsed at the same time: for, when the second and third are in one direction, the first is in the opposite direction; consequently, when the first is eclipsed, the other two must be between the sun and Jupiter. The instant of the beginning or end of an eclipse of a satellite marks the same instant of absolute time to all the inhabitants of the earth; therefore, the time of these eclipses observed by a traveller, when compared with the time of the eclipse computed for Greenwich, or any other fixed meridian (N. 95), gives the difference of the meridians in time, and, consequently, the longitude of the place of observation. The longitude is determined with extreme precision whenever it is possible to convey the time instantaneously by means of electricity from one place to another, since it obviates the errors of clocks and chronometers. The eclipses of Jupiter’s satellites have been the means of a discovery which, though not so immediately applicable to the wants of man, unfolds one of the properties of light—that medium without whose cheering influence all the beauties of the creation would have been to us a blank. It is observed, that those eclipses of the first satellite which happen when Jupiter is near conjunction 31(N. 96), are later by 16ʹ 26ʺ·6 than those which take place when the planet is in opposition. As Jupiter is nearer to us when in opposition by the whole breadth of the earth’s orbit than when in conjunction, this circumstance is to be attributed to the time employed by the rays of light in crossing the earth’s orbit, a distance of about 190,000,000 of miles; whence it is estimated that light travels at the rate of 192,000 miles in one second. Such is its velocity, that the earth, moving at the rate of nineteen miles in a second, would take two months to pass through a distance which a ray of light would dart over in eight minutes. The subsequent discovery of the aberration of light has fully confirmed this astonishing result.
Objects appear to be situate in the direction of the rays which proceed from them. Were light propagated instantaneously, every object, whether at rest or in motion, would appear in the direction of these rays; but, as light takes some time to travel, we see Jupiter in conjunction, by means of rays that left him 16m 26s·6 before; but, during that time, we have changed our position, in consequence of the motion of the earth in its orbit: we therefore refer Jupiter to a place in which he is not. His true position is in the diagonal (N. 97) of the parallelogram, whose sides are in the ratio of the velocity of light to the velocity of the earth in its orbit, which is as 192,000 to 19, or nearly as 10,000 to 1. In consequence of the aberration of light, the heavenly bodies seem to be in places in which they are not. In fact, if the earth were at rest, rays from a star would pass along the axis of a telescope directed to it; but, if the earth were to begin to move in its orbit with its usual velocity, these rays would strike against the side of the tube; it would, therefore, be necessary to incline the telescope a little, in order to see the star. The angle contained between the axis of the telescope and a line drawn to the true place of the star is its aberration, which varies in quantity and direction in different parts of the earth’s orbit; but, as it is only 20ʺ·481, it is insensible in ordinary cases (N. 98).
The velocity of light deduced from the observed aberration of the fixed stars perfectly corresponds with that given by the eclipses of the first satellite. The same result, obtained from sources so different, leaves not a doubt of its truth. Many such beautiful coincidences, derived from circumstances apparently the most unpromising and dissimilar, occur in physical astronomy, 32and prove connections which we might otherwise be unable to trace. The identity of the velocity of light, at the distance of Jupiter, and on the earth’s surface, shows that its velocity is uniform; and as light consists in the vibrations of an elastic medium or ether filling space, the uniformity of its velocity shows that the density of the medium throughout the whole extent of the solar system must be proportional to its elasticity (N. 99). Among the fortunate conjectures which have been confirmed by subsequent experience, that of Bacon is not the least remarkable, “It produces in me,” says the restorer of true philosophy, “a doubt whether the face of the serene and starry heavens be seen at the instant it really exists, or not till some time later: and whether there be not, with respect to the heavenly bodies, a true time and an apparent time, no less than a true place and an apparent place, as astronomers say, on account of parallax. For it seems incredible that the species or rays of the celestial bodies can pass through the immense interval between them and us in an instant, or that they do not even require some considerable portion of time.”
Great discoveries generally lead to a variety of conclusions: the aberration of light affords a direct proof of the motion of the earth in its orbit; and its rotation is proved by the theory of falling bodies, since the centrifugal force it induces retards the oscillations of the pendulum (N. 100) in going from the pole to the equator. Thus a high degree of scientific knowledge has been requisite to dispel the errors of the senses (N. 237).
The little that is known of the theories of the satellites of Saturn and Uranus is, in all respects, similar to that of Jupiter. Saturn is accompanied by eight satellites. The seventh is about the size of Mars, and the eighth was simultaneously discovered by Mr. Bond in America, and that distinguished astronomer Mr. Lassell, of Liverpool. The orbits of the two last have a sensible inclination to the plane of the ring; but the great compression of Saturn occasions the other satellites to move nearly in the plane of his equator. So many circumstances must concur to render the two interior satellites visible, that they have very rarely been seen. They move exactly at the edge of the ring, and their orbits never deviate from its plane. In 1789 Sir William Herschel saw them like beads, threading the slender line of light which the ring is reduced to when seen edgewise 33from the earth. And for a short time he perceived them advancing off it at each end, when turning round in their orbits. The eclipses of the exterior satellites only take place when the ring is in this position. Mr. Lassell, with a powerful telescope, made by himself, has seen Iapetus, the nearest of the two, on several occasions, even when the opening of the ring was very wide, which made it extremely difficult to see so minute an object. Of the situation of the equator of Uranus we know nothing, nor of his compression; but the orbits of his satellites are nearly perpendicular to the plane of the ecliptic; and, by analogy, they ought to be in the plane of his equator. Uranus is so remote that he has more the appearance of a planetary nebula than a planet, which renders it extremely difficult to distinguish the satellites at all; and quite hopeless without such a telescope as is rarely to be met with even in observatories. Sir William Herschel discovered the two that are farthest from the planet, and ascertained their approximate periods, which his son afterwards determined to be 13d 11h 7m 12s·6 and 8d 16h 56m 28s·6 respectively. The orbits of both seem to have an inclination of about 101°·2 to the plane of the ecliptic. The two interior satellites are so faint and small, and so near the edge of the planet, that they can with difficulty be seen even under the most favourable circumstances: however, Mr. Lassell has ascertained that the more distant of the two revolves about Uranus in 4 days, and that nearest to the planet in 21⁄2 days, and from a long and minute examination he is convinced that the system only consists of four satellites. Soon after Neptune was seen Mr. Lassell discovered the only satellite known to belong to that planet. The satellites of Uranus and Neptune, the two planets on the remotest verge of the solar system, offer the singular and only instance of a revolution from east to west, while all the planets and all the other satellites revolve from west to east. Retrograde motion is occasionally met with in the comets and double stars.
Lunar Theory—Periodic Perturbations of the Moon—Equation of Centre—Evection—Variation—Annual Equation—Direct and Indirect Action of Planets—The Moon’s Action on the Earth disturbs her own Motion—Excentricity and Inclination of Lunar Orbit invariable—Acceleration—Secular Variation in Nodes and Perigee—Motion of Nodes and Perigee inseparably connected with the Acceleration—Nutation of Lunar Orbit—Form and Internal Structure of the Earth determined from it—Lunar, Solar, and Planetary Eclipses—Occultations and Lunar Distances—Mean Distance of the Sun from the Earth obtained from Lunar Theory—Absolute Distances of the Planets, how found.
Our constant companion, the moon, next claims our attention. Several circumstances concur to render her motions the most interesting, and at the same time the most difficult to investigate, of all the bodies of our system. In the solar system, planet troubles planet; but, in the lunar theory, the sun is the great disturbing cause, his vast distance being compensated by his enormous magnitude, so that the motions of the moon are more irregular than those of the planets; and, on account of the great ellipticity of her orbit, and the size of the sun, the approximations to her motions are tedious and difficult, beyond what those unaccustomed to such investigations could imagine. The average distance of the moon from the centre of the earth is only 238,793 miles, so that her motion among the stars is perceptible in a few hours. She completes a circuit of the heavens in 27d 7h 43m 11s·5, moving in an orbit whose excentricity is about 12,985 miles. The moon is about four hundred times nearer to the earth than the sun. The proximity of the moon to the earth keeps them together. For so great is the attraction of the sun, that, if the moon were farther from the earth, she would leave it altogether, and would revolve as an independent planet about the sun.
The disturbing action (N. 101) of the sun on the moon is equivalent to three forces. The first, acting in the direction of the line joining the moon and earth, increases or diminishes her gravity to the earth. The second, acting in the direction of a 35tangent to her orbit, disturbs her motion in longitude. And the third, acting perpendicularly to the plane of her orbit, disturbs her motion in latitude; that is, it brings her nearer to, or removes her farther from, the plane of the ecliptic than she would otherwise be. The periodic perturbations in the moon, arising from these forces, are perfectly similar to the periodic perturbations of the planets. But they are much greater and more numerous; because the sun is so large, that many inequalities which are quite insensible in the motions of the planets, are of great magnitude in those of the moon. Among the innumerable periodic inequalities to which the moon’s motion in longitude is liable, the most remarkable are, the Equation of the Centre, which is the difference between the moon’s mean and true longitude, the Evection, the Variation, and the Annual Equation. The disturbing force which acts in the line joining the moon and earth produces the Evection: it diminishes the excentricity of the lunar orbit in conjunction and opposition, thereby making it more circular, and augments it in quadrature, which consequently renders it more elliptical. The period of this inequality is less than thirty-two days. Were the increase and diminution always the same, the Evection would only depend upon the distance of the moon from the sun; but its absolute value also varies with her distance from the perigee (N. 102) of her orbit. Ancient astronomers, who observed the moon solely with a view to the prediction of eclipses, which can only happen in conjunction and opposition, where the excentricity is diminished by the Evection, assigned too small a value to the ellipticity of her orbit (N. 103). The Evection was discovered by Ptolemy from observation, about A.D. 140. The Variation produced by the tangential disturbing force, which is at its maximum when the moon is 45° distant from the sun, vanishes when that distance amounts to a quadrant, and also when the moon is in conjunction and opposition; consequently, that inequality never could have been discovered from the eclipses: its period is half a lunar month (N. 104). The Annual Equation depends upon the sun’s distance from the earth: it arises from the moon’s motion being accelerated when that of the earth is retarded, and vice versâ—for, when the earth is in its perihelion, the lunar orbit is enlarged by the action of the sun; therefore, the moon requires more time to perform her revolution. But, as the earth approaches its aphelion, the 36moon’s orbit contracts, and less time is necessary to accomplish her motion—its period, consequently, depends upon the time of the year. In the eclipses the Annual Equation combines with the Equation of the Centre of the terrestrial orbit, so that ancient astronomers imagined the earth’s orbit to have a greater excentricity than modern astronomers assign to it.
The planets disturb the motion of the moon both directly and indirectly; their action on the earth alters its relative position with regard to the sun and moon, and occasions inequalities in the moon’s motion, which are more considerable than those arising from their direct action; for the same reason the moon, by disturbing the earth, indirectly disturbs her own motion. Neither the excentricity of the lunar orbit, nor its mean inclination to the plane of the ecliptic, have experienced any changes from secular inequalities; for, although the mean action of the sun on the moon depends upon the inclination of the lunar orbit to the ecliptic, and the position of the ecliptic is subject to a secular inequality, yet analysis shows that it does not occasion a secular variation in the inclination of the lunar orbit, because the action of the sun constantly brings the moon’s orbit to the same inclination to the ecliptic. The mean motion, the nodes, and the perigee, however, are subject to very remarkable variations.
From the eclipse observed at Babylon, on the 19th of March, seven hundred and twenty-one years before the Christian era, the place of the moon is known from that of the sun at the instant of opposition (N. 83), whence her mean longitude may be found. But the comparison of this mean longitude with another mean longitude, computed back for the instant of the eclipse from modern observations, shows that the moon performs her revolution round the earth more rapidly and in a shorter time now than she did formerly, and that the acceleration in her mean motion has been increasing from age to age as the square of the time (N. 105). All ancient and intermediate eclipses confirm this result. As the mean motions of the planets have no secular inequalities, this seemed to be an unaccountable anomaly. It was at one time attributed to the resistance of an ethereal medium pervading space, and at another to the successive transmission of the gravitating force. But, as La Place proved that neither of these causes, even if they exist, have any influence on the motions of the lunar perigee (N. 102) or nodes, 37they could not affect the mean motion; a variation in the mean motion from such causes being inseparably connected with variations in the motions of the perigee and nodes. That great mathematician, in studying the theory of Jupiter’s satellites, perceived that the secular variation in the elements of Jupiter’s orbit, from the action of the planets, occasions corresponding changes in the motions of the satellites, which led him to suspect that the acceleration in the mean motion of the moon might be connected with the secular variation in the excentricity of the terrestrial orbit. Analysis has shown that he assigned the true cause of the acceleration.
It is proved that the greater the excentricity of the terrestrial orbit, the greater is the disturbing action of the sun on the moon. Now, as the excentricity has been decreasing for ages, the effect of the sun in disturbing the moon has been diminishing during that time. Consequently the attraction of the earth has had a more and more powerful effect on the moon, and has been continually diminishing the size of the lunar orbit. So that the moon’s velocity has been gradually augmenting for many centuries to balance the increase of the earth’s attraction. This secular increase in the moon’s velocity is called the Acceleration, a name peculiarly appropriate at present, and which will continue to be so for a vast number of ages; because, as long as the earth’s excentricity diminishes, the moon’s mean motion will be accelerated; but when the excentricity has passed its minimum, and begins to increase, the mean motion will be retarded from age to age. The secular acceleration is now about 11ʺ·9, but its effect on the moon’s place increases as the square of the time (N. 106). It is remarkable that the action of the planets, thus reflected by the sun to the moon, is much more sensible than their direct action either on the earth or moon. The secular diminution in the excentricity, which has not altered the equation of the centre of the sun by eight minutes since the earliest recorded eclipses, has produced a variation of about 1° 48ʹ in the moon’s longitude, and of 7° 12ʹ in her mean anomaly (N. 107).
The action of the sun occasions a rapid but variable motion in the nodes and perigee of the lunar orbit. Though the nodes recede during the greater part of the moon’s revolution, and advance during the smaller, they perform their sidereal revolution in 6793d 9h 23m 9s·3, or about 186⁄10 years; and the 38perigee accomplishes a revolution, called of the moon’s apsides, in 3232d 13h 48m 29s·6, or a little more than nine years, notwithstanding its motion is sometimes retrograde and sometimes direct: but such is the difference between the disturbing energy of the sun and that of all the planets put together, that it requires no less than 109,830 years for the greater axis of the terrestrial orbit to do the same, moving at the rate of 11ʺ·8 annually. The form of the earth has no sensible effect either on the lunar nodes or apsides. It is evident that the same secular variation which changes the sun’s distance from the earth, and occasions the acceleration in the moon’s mean motion, must affect the nodes and perigee. It consequently appears, from theory as well as observation, that both these elements are subject to a secular inequality, arising from the variation in the excentricity of the earth’s orbit, which connects them with the Acceleration, so that both are retarded when the mean motion is anticipated. The secular variations in these three elements are in the ratio of the numbers 3, 0·735, and 1; whence the three motions of the moon, with regard to the sun, to her perigee, and to her nodes, are continually accelerated, and their secular equations are as the numbers 1, 4·702, and 0·612. A comparison of ancient eclipses observed by the Arabs, Greeks, and Chaldeans, imperfect as they are, with modern observations, confirms these results of analysis. Future ages will develop these great inequalities, which at some most distant period will amount to many circumferences (N. 108). They are, indeed, periodic; but who shall tell their period? Millions of years must elapse before that great cycle is accomplished.
The moon is so near, that the excess of matter at the earth’s equator occasions periodic variations in her longitude, and also that remarkable inequality in her latitude, already mentioned as a nutation in the lunar orbit, which diminishes its inclination to the ecliptic when the moon’s ascending node coincides with the equinox of spring, and augments it when that node coincides with the equinox of autumn. As the cause must be proportional to the effect, a comparison of these inequalities, computed from theory, with the same given by observation, shows that the compression of the terrestrial spheroid, or the ratio of the difference between the polar and the equatorial diameters, to the diameter of the equator, is 1⁄305·05. It is proved analytically, that, if a fluid mass of homogeneous matter, whose particles attract each other 39inversely as the squares of the distance, were to revolve about an axis as the earth does, it would assume the form of a spheroid whose compression is 1⁄230. Since that is not the case, the earth cannot be homogeneous, but must decrease in density from its centre to its circumference. Thus the moon’s eclipses show the earth to be round; and her inequalities not only determine the form, but even the internal structure of our planet; results of analysis which could not have been anticipated. Similar inequalities in the motions of Jupiter’s satellites prove that his mass is not homogeneous, and that his compression is 1⁄13·8. His equatorial diameter exceeds his polar diameter by about 6000 miles.
The phases (N. 109) of the moon, which vary from a slender silvery crescent soon after conjunction, to a complete circular disc of light in opposition, decrease by the same degrees till the moon is again enveloped in the morning beams of the sun. These changes regulate the returns of the eclipses. Those of the sun can only happen in conjunction, when the moon, coming between the earth and the sun, intercepts his light. Those of the moon are occasioned by the earth intervening between the sun and moon when in opposition. As the earth is opaque and nearly spherical, it throws a conical shadow on the side of the moon opposite to the sun, the axis of which passes through the centres of the sun and earth (N. 110). The length of the shadow terminates at the point where the apparent diameters (N. 111) of the sun and earth would be the same. When the moon is in opposition, and at her mean distance, the diameter of the sun would be seen from her centre under an angle of 1918ʺ·1. That of the earth would appear under an angle of 6908ʺ·3. So that the length of the shadow is at least three times and a half greater than the distance of the moon from the earth, and the breadth of the shadow, where it is traversed by the moon, is about eight-thirds of the lunar diameter. Hence the moon would be eclipsed every time she is in opposition, were it not for the inclination of her orbit to the plane of the ecliptic, in consequence of which the moon, when in opposition, is either above or below the cone of the earth’s shadow, except when in or near her nodes. Her position with regard to them occasions all the varieties in the lunar eclipses. Every point of the moon’s surface successively loses the light of different parts of the sun’s disc before being eclipsed. Her brightness therefore gradually diminishes before she plunges 40into the earth’s shadow. The breadth of the space occupied by the penumbra (N. 112) is equal to the apparent diameter of the sun, as seen from the centre of the moon. The mean duration of a revolution of the sun, with regard to the node of the lunar orbit, is to the duration of a synodic revolution (N. 113) of the moon as 223 to 19. So that, after a period of 223 lunar months, the sun and moon would return to the same relative position with regard to the node of the moon’s orbit, and therefore the eclipses would recur in the same order were not the periods altered by irregularities in the motions of the sun and moon. In lunar eclipses, our atmosphere bends the sun’s rays which pass through it all round into the cone of the earth’s shadow. And as the horizontal refraction (N. 114) or bending of the rays surpasses half the sum of the semidiameters of the sun and moon, divided by their mutual distance, the centre of the lunar disc, supposed to be in the axis of the shadow, would receive the rays from the same point of the sun, round all sides of the earth; so that it would be more illuminated than in full moon, if the greater portion of the light were not stopped or absorbed by the atmosphere. Instances are recorded where this feeble light has been entirely absorbed, so that the moon has altogether disappeared in her eclipses.
The sun is eclipsed when the moon intercepts his rays (N. 115). The moon, though incomparably smaller than the sun, is so much nearer the earth, that her apparent diameter differs but little from his, but both are liable to such variations that they alternately surpass one another. Were the eye of a spectator in the same straight line with the centres of the sun and moon, he would see the sun eclipsed. If the apparent diameter of the moon surpassed that of the sun, the eclipse would be total. If it were less, the observer would see a ring of light round the disc of the moon, and the eclipse would be annular, as it was on the 17th of May, 1836, and on the 15th of March, 1858. If the centre of the moon should not be in the straight line joining the centres of the sun and the eye of the observer, the moon might only eclipse a part of the sun. The variation, therefore, in the distances of the sun and moon from the centre of the earth, and of the moon from her node at the instant of conjunction, occasions great varieties in the solar eclipses. Besides, the height of the moon above the horizon 41changes her apparent diameter, and may augment or diminish the apparent distances of the centres of the sun and moon, so that an eclipse of the sun may occur to the inhabitants of one country, and not to those of another. In this respect the solar eclipses differ from the lunar, which are the same for every part of the earth where the moon is above the horizon. In solar eclipses, the light reflected by the atmosphere diminishes the obscurity they produce. Even in total eclipses the higher part of the atmosphere is enlightened by a part of the sun’s disc, and reflects its rays to the earth. The whole disc of the new moon is frequently visible from atmospheric reflection. During the eclipse of the 19th of March, 1849, the spots on the lunar disc were distinctly visible, and during that of 1856 the moon was like a beautiful rose-coloured ball floating in the ether: the colour is owing to the refraction of the sun’s light passing through the earth’s atmosphere.
In total solar eclipses the slender luminous arc that is visible for a few seconds before the sun vanishes and also before he reappears, resembles a string of pearls surrounding the dark edge of the moon; it is occasioned by the sun’s rays passing between the tops of the lunar mountains: it occurs likewise in annular eclipses.
A phenomenon altogether unprecedented was seen during the total eclipse of the sun which happened on the 8th of July, 1842. The moon was like a black patch on the sky surrounded by a faint whitish light or corona about the eighth of the moon’s diameter in breadth, which is supposed to be the solar atmosphere rendered visible by the intervention of the moon. In this whitish corona there appeared three rose-coloured flames like the teeth of a saw. Similar flames were also seen in the white corona of the total eclipse which took place in 1851, and a long rose-coloured chain of what appeared to be jagged mountains or sierras united at the base by a red band seemed to be raised into the corona by mirage; but there is no doubt that the corona and red phenomena belong to the sun. This red chain was so bright that Mr. Airy saw it illuminate the northern horizon through an azimuth of 90° with red light. M. Faye attributes the rose-coloured protuberances to the constitution of the sun, which, like Sir William Herschel, he conceives to be an incandescent globe, consisting of two concentric parts of very unequal density, the internal part being a dark spherical mass, the external a very 42extensive atmosphere, at a certain height in which there is a stratum of luminous clouds which constitutes the photosphere of the sun; above this rises his real atmosphere, so rare as to be only visible as a white aureola or corona during total and annular eclipses. M. Faye conceives that from the central mass gaseous eruptions issue, which form the spots by dissipating and partly extinguishing the luminous clouds, and then rising into the rare atmosphere above that they appear as rose-coloured protuberances during annular eclipses. He estimates that the volume of these vapours sometimes surpasses that of the earth a thousand or even two thousand times. Sir William Herschel attributed the spots to occasional openings in the luminous coating, which seems to be always in motion; but whatever the cause of the spots may be, it is certainly periodical. The white corona and beads were seen during the eclipse of the 15th March, 1858, but there were no rose-coloured appearances, in England at least; but the sky was clouded, so that the eclipse was only visible at intervals.
Planets sometimes eclipse one another. On the 17th of May, 1737, Mercury was eclipsed by Venus near their inferior conjunction; Mars passed over Jupiter on the 9th of January, 1591; and on the 30th of October, 1825, the moon eclipsed Saturn. These phenomena, however, happen very seldom, because all the planets, or even a part of them, are very rarely seen in conjunction at once; that is, in the same part of the heavens at the same time. More than 2500 years before our era the five great planets were in conjunction. On the 15th of September, 1186, a similar assemblage took place between the constellations of Virgo and Libra; and in 1801 the Moon, Jupiter, Saturn, and Venus were united in the heart of the Lion. These conjunctions are so rare, that Lalande has computed that more than seventeen millions of millions of years separate the epochs of the contemporaneous conjunctions of the six great planets.
The motions of the moon have now become of more importance to the navigator and geographer than those of any other heavenly body, from the precision with which terrestrial longitude is determined by occultations of stars, and by lunar distances. In consequence of the retrograde motion of the nodes of the lunar orbit, at the rate of 3ʹ 10ʺ·64 daily, these points make a tour of the heavens in a little more than eighteen years and a half. 43This causes the moon to move round the earth in a kind of spiral, so that her disc at different times passes over every point in a zone of the heavens extending rather more than 5° 9ʹ on each side of the ecliptic. It is therefore evident that at one time or other she must eclipse every star and planet she meets with in this space. Therefore the occultation of a star by the moon is a phenomenon of frequent occurrence. The moon seems to pass over the star, which almost instantaneously vanishes at one side of her disc, and after a short time as suddenly reappears on the other. A lunar distance is the observed distance of the moon from the sun, or from a particular star or planet, at any instant. The lunar theory is brought to such perfection, that the times of these phenomena, observed under any meridian, when compared with those computed for that of Greenwich, and given in the Nautical Almanac, furnish the longitude of the observer within a few miles (N. 95.)
From the lunar theory, the mean distance of the sun from the earth, and thence the whole dimensions of the solar system, are known; for the forces which retain the earth and moon in their orbits are respectively proportional to the radii vectores of the earth and moon, each being divided by the square of its periodic time. And, as the lunar theory gives the ratio of the forces, the ratio of the distances of the sun and moon from the earth is obtained. Hence it appears that the sun’s mean distance from the earth is 399·7 or nearly 400 times greater than that of the moon. The method of finding the absolute distances of the celestial bodies, in miles, is in fact the same with that employed in measuring the distances of terrestrial objects. From the extremities of a known base (N. 116), the angles which the visual rays from the object form with it are measured; their sum subtracted from two right angles gives the angle opposite the base; therefore, by trigonometry, all the angles and sides of the triangle may be computed—consequently the distance of the object is found. The angle under which the base of the triangle is seen from the object is the parallax of that object. It evidently increases and decreases with the distance. Therefore the base must be very great indeed to be visible from the celestial bodies. The globe itself, whose dimensions are obtained by actual admeasurement, furnishes a standard of measures with which we compare the distances, masses, densities, and volumes of the sun and planets.
Form of the Earth and Planets—Figure of a Homogeneous Spheroid in Rotation—Figure of a Spheroid of variable Density—Figure of the Earth, supposing it to be an Ellipsoid of Revolution—Mensuration of a Degree of the Meridian—Compression and Size of the Earth from Degrees of Meridian—Figure of Earth from the Pendulum.
The theoretical investigation of the figure of the earth and planets is so complicated, that neither the geometry of Newton, nor the refined analysis of La Place, has attained more than an approximation. The solution of that difficult problem has been accomplished by our distinguished countryman Mr. Ivory. The investigation has been conducted by successive steps, beginning with a simple case, and then proceeding to the more difficult. But, in all, the forces which occasion the revolutions of the earth and planets are omitted, because, by acting equally upon all the particles, they do not disturb their mutual relations. A fluid mass of uniform density, whose particles mutually gravitate to each other, will assume the form of a sphere when at rest. But, if the sphere begins to revolve, every particle will describe a circle (N. 117), having its centre in the axis of revolution. The planes of all these circles will be parallel to one another and perpendicular to the axis, and the particles will have a tendency to fly from that axis in consequence of the centrifugal force arising from the velocity of rotation. The force of gravity is everywhere perpendicular to the surface (N. 118), and tends to the interior of the fluid mass; whereas the centrifugal force acts perpendicularly to the axis of rotation, and is directed to the exterior. And, as its intensity diminishes with the distance from the axis of rotation, it decreases from the equator to the poles, where it ceases. Now it is clear that these two forces are in direct opposition to each other in the equator alone, and that gravity is there diminished by the whole effect of the centrifugal force, whereas, in every other part of the fluid, the centrifugal force is resolved into two parts, one of which, being perpendicular to the surface, diminishes 45the force of gravity; but the other, being at a tangent to the surface, urges the particles towards the equator, where they accumulate till their numbers compensate the diminution of gravity, which makes the mass bulge at the equator, and become flattened at the poles. It appears, then, that the influence of the centrifugal force is most powerful at the equator, not only because it is actually greater there than elsewhere, but because its whole effect is employed in diminishing gravity, whereas, in every other point of the fluid mass, it is only a part that is so employed. For both these reasons, it gradually decreases towards the poles, where it ceases. On the contrary, gravity is least at the equator, because the particles are farther from the centre of the mass, and increases towards the poles, where it is greatest. It is evident, therefore, that, as the centrifugal force is much less than the force of gravity—gravitation, which is the difference between the two, is least at the equator, and continually increases towards the poles, where it is a maximum. On these principles Sir Isaac Newton proved that a homogeneous fluid (N. 119) mass in rotation assumes the form of an ellipsoid of revolution (N. 120), whose compression is 1⁄230. Such, however, cannot be the form of the earth, because the strata increase in density towards the centre. The lunar inequalities also prove the earth to be so constructed; it was requisite, therefore, to consider the fluid mass to be of variable density. Including this condition, it has been found that the mass, when in rotation, would still assume the form of an ellipsoid of revolution (N. 120); that the particles of equal density would arrange themselves in concentric elliptical strata (N. 121), the most dense being in the centre; but that the compression or flattening would be less than in the case of the homogeneous fluid. The compression is still less when the mass is considered to be, as it actually is, a solid nucleus, decreasing regularly in density from the centre to the surface, and partially covered by the ocean, because the solid parts, by their cohesion, nearly destroy that part of the centrifugal force which gives the particles a tendency to accumulate at the equator, though not altogether; otherwise the sea, by the superior mobility of its particles, would flow towards the equator and leave the poles dry. Besides, it is well known that the continents at the equator are more elevated than they are in higher latitudes. It is also necessary for the equilibrium of the ocean that its density 46should be less than the mean density of the earth, otherwise the continents would be perpetually liable to inundations from storms and other causes. On the whole, it appears from theory, that a horizontal line passing round the earth through both poles must be nearly an ellipse, having its major axis in the plane of the equator, and its minor axis coincident with the axis of the earth’s rotation (N. 122). It is easy to show, in a spheroid whose strata are elliptical, that the increase in the length of the radii (N. 123), the decrease of gravitation, and the increase in the length of the arcs of the meridian, corresponding to angles of one degree, from the poles to the equator, are all proportional to the square of the cosine of the latitude (N. 124). These quantities are so connected with the ellipticity of the spheroid, that the total increase in the length of the radii is equal to the compression or flattening, and the total diminution in the length of the arcs is equal to the compression, multiplied by three times the length of an arc of one degree at the equator. Hence, by measuring the meridian curvature of the earth, the compression, and consequently its figure, become known. This, indeed, is assuming the earth to be an ellipsoid of revolution; but the actual measurement of the globe will show how far it corresponds with that solid in figure and constitution.
The courses of the great rivers, which are in general navigable to a considerable extent, prove that the curvature of the land differs but little from that of the ocean; and, as the heights of the mountains and continents are inconsiderable when compared with the magnitude of the earth, its figure is understood to be determined by a surface at every point perpendicular to the direction of gravitation, or of the plumb-line, and is the same which the sea would have if it were continued all round the earth beneath the continents. Such is the figure that has been measured in the following manner:—
A terrestrial meridian is a line passing through both poles, all the points of which have their noon contemporaneously. Were the lengths and curvatures of different meridians known, the figure of the earth might be determined. But the length of one degree is sufficient to give the figure of the earth, if it be measured on different meridians, and in a variety of latitudes. For, if the earth were a sphere, all degrees would be of the same length; but, if not, the lengths of the degrees would be greater, 47exactly in proportion as the curvature is less. A comparison of the length of a degree in different parts of the earth’s surface will therefore determine its size and form.
An arc of the meridian may be measured by determining the latitude of its extreme points by astronomical observations (N. 125), and then measuring the distance between them in feet or fathoms. The distance thus determined on the surface of the earth, divided by the degrees and parts of a degree contained in the difference of the latitudes, will give the exact length of one degree, the difference of the latitudes being the angle contained between the verticals at the extremities of the arc. This would be easily accomplished were the distance unobstructed and on a level with the sea. But, on account of the innumerable obstacles on the surface of the earth, it is necessary to connect the extreme points of the arc by a series of triangles (N. 126), the sides and angles of which are either measured or computed, so that the length of the arc is ascertained with much laborious calculation. In consequence of the irregularities of the surface each triangle is in a different plane. They must therefore be reduced by computation to what they would have been had they been measured on the surface of the sea. And, as the earth may in this case be esteemed spherical, they require a correction to reduce them to spherical triangles. The officers who conducted the trigonometrical survey, in measuring 500 feet of a base in Ireland twice over, found that the difference in the two measurements did not amount to the 800th part of an inch; and in the General Survey of Great Britain, five bases were measured from 5 to 7 miles long, and some of them 400 miles apart, yet, when connected by series of triangles, the measured and computed lengths did not differ by more than 3 inches, an unparalleled degree of accuracy; but such is the accuracy with which these operations are conducted.
Arcs of the meridian have been measured in a variety of latitudes in both hemispheres, as well as arcs perpendicular to the meridian. From these measurements it appears that the length of the degrees increases from the equator to the poles, nearly in proportion to the square of the sine of the latitude (N. 127). Consequently, the convexity of the earth diminishes from the equator to the poles.
Were the earth an ellipsoid of revolution, the meridians would be ellipses whose lesser axes would coincide with the axis of 48rotation, and all the degrees measured between the pole and the equator would give the same compression when combined two and two. That, however, is far from being the case. Scarcely any of the measurements give exactly the same results, chiefly on account of local attractions, which cause the plumb-line to deviate from the vertical. The vicinity of mountains produces that effect. One of the most remarkable anomalies of this kind has been observed in certain localities of northern Italy, where the action of some dense subterraneous matter causes the plumb-line to deviate seven or eight times more than it did from the attraction of Chimborazo, in the observations of Bouguer, while measuring a degree of the meridian at the equator. In consequence of this local attraction, the degrees of the meridian in that part of Italy seem to increase towards the equator through a small space, instead of decreasing, as if the earth was drawn out at the poles, instead of being flattened.
Many other discrepancies occur, but from the mean of the five principal measurements of arcs in Peru, India, France, England, and Lapland, Mr. Ivory has deduced that the figure which most nearly follows this law is an ellipsoid of revolution whose equatorial radius is 3962·824 miles, and the polar radius 3949·585 miles. The difference, or 13·239 miles, divided by the equatorial radius, is 1⁄299 nearly[3] (N. 128). This fraction is called the compression of the earth, and does not differ much from that given by the lunar inequalities. Since the preceding quantities were determined, arcs of the meridian have been measured in various parts of the globe, of which the most extensive are the Russian arc of 25° 20ʹ between the Glacial Sea and the Danube, conducted under the superintendence of M. Struve, and the Indian arc extended to 21° 21ʹ, by Colonel Everest. The compression deduced by Bessel from the sum of ten arcs is 2983⁄4, the equatorial radius 3962·802, and the polar 3949·554 miles, whilst Mr. Airy arrives at an almost identical result (3962·824, 3949·585, and 29883⁄100) from a consideration of all the arcs, measured up to 1831, including the great Indian and Russian ones. If we assume the earth to be a sphere, the length of a degree of the meridian is 6914⁄100 English miles. Therefore 360 degrees, or the whole equatorial 49circumference of the globe, is 24,899 English miles. Eratosthenes, who died 194 years before the Christian era, was the first to give an approximate value of the earth’s circumference, by the measurement of an arc between Alexandria and Syene.
There is another method of finding the figure of the earth, totally different from the preceding, solely depending upon the increase of gravitation from the equator to the poles. The force of gravitation at any place is measured by the descent of a heavy body during the first second of its fall. And the intensity of the centrifugal force is measured by the deflection of any point from the tangent in a second. For, since the centrifugal force balances the attraction of the earth, it is an exact measure of the gravitating force. Were the attraction to cease, a body on the surface of the earth would fly off in the tangent by the centrifugal force, instead of bending round in the circle of rotation. Therefore, the deflection of the circle from the tangent in a second measures the intensity of the earth’s attraction, and is equal to the versed sine of the arc described during that time, a quantity easily determined from the known velocity of the earth’s rotation. Whence it has been found that at the equator the centrifugal force is equal to the 289th part of gravity. Now, it is proved by analysis that, whatever the constitution of the earth and planets may be, if the intensity of gravitation at the equator be taken equal to unity, the sum of the compression of the ellipsoid, and the whole increase of gravitation from the equator to the pole, is equal to five halves of the ratio of the centrifugal force to gravitation at the equator. This quantity with regard to the earth is 5⁄2 of 1⁄289 or 1⁄115·2. Consequently, the compression of the earth is equal to 1⁄115·2 diminished by the whole increase of gravitation. So that its form will be known, if the whole increase of gravitation from the equator to the pole can be determined by experiment. This has been accomplished by a method founded upon the following considerations:—If the earth were a homogeneous sphere without rotation, its attraction on bodies at its surface would be everywhere the same. If it be elliptical and of variable density, the force of gravity, theoretically, ought to increase from the equator to the pole, as unity plus a constant quantity multiplied into the square of the sine of the latitude (N. 127). But for a spheroid in rotation the centrifugal force varies, by the laws of mechanics, as the square of the sine of the latitude, from 50the equator, where it is greatest, to the pole, where it vanishes. And, as it tends to make bodies fly off the surface, it diminishes the force of gravity by a small quantity. Hence, by gravitation, which is the difference of these two forces, the fall of bodies ought to be accelerated from the equator to the poles proportionably to the square of the sine of the latitude; and the weight of the same body ought to increase in that ratio. This is directly proved by the oscillations of the pendulum (N. 129), which, in fact, is a falling body; for, if the fall of bodies be accelerated, the oscillations will be more rapid: in order, therefore, that they may always be performed in the same time, the length of the pendulum must be altered. By numerous and careful experiments it is proved that a pendulum, which oscillates 86,400 times in a mean day at the equator, will do the same at every point of the earth’s surface, if its length be increased progressively to the pole, as the square of the sine of the latitude.
From the mean of these it appears that the whole decrease of gravitation from the poles to the equator is 0·0051449, which, subtracted from 1⁄115·2, shows that the compression of the terrestrial spheroid is about 1⁄285·26. This value has been deduced by the late Mr. Baily, president of the Astronomical Society, who devoted much attention to this subject; at the same time, it may be observed that no two sets of pendulum experiments give the same result, probably from local attractions. The compression obtained by this method does not differ much from that given by the lunar inequalities, nor from the arcs in the direction of the meridian, and those perpendicular to it. The near coincidence of these three values, deduced by methods so entirely independent of each other, shows that the mutual tendencies of the centres of the celestial bodies to one another, and the attraction of the earth for bodies at its surface, result from the reciprocal attraction of all their particles. Another proof may be added. The nutation of the earth’s axis and the precession of the equinoxes (N. 146) are occasioned by the action of the sun and moon on the protuberant matter at the earth’s equator. And, although these inequalities do not give the absolute value of the terrestrial compression, they show that the fraction expressing it is comprised between the limits 1⁄279 and 1⁄573.
It might be expected that the same compression should result from each, if the different methods of observation could be made without error. This, however, is not the case; for after allowance 51has been made for every cause of error, such discrepancies are found, both in the degrees of the meridian and in the length of the pendulum, as show that the figure of the earth is very complicated. But they are so small, when compared with the general results, that they may be disregarded. The compression deduced from the mean of the whole appears not to differ much from 1⁄300; that given by the lunar theory has the advantage of being independent of the irregularities of the earth’s surface and of local attractions. The regularity with which the observed variation in the length of the pendulum follows the law of the square of the sine of the latitude proves the strata to be elliptical, and symmetrically disposed round the centre of gravity of the earth, which affords a strong presumption in favour of its original fluidity. It is remarkable how little influence the sea has on the variation of the lengths of the arcs of the meridian, or on gravitation; neither does it much affect the lunar inequalities, from its density being only about a fifth of the mean density of the earth. For, if the earth were to become fluid, after being stripped of the ocean, it would assume the form of an ellipsoid of revolution whose compression is 1⁄304·8, which differs very little from that determined by observation, and proves, not only that the density of the ocean is inconsiderable, but that its mean depth is very small. There are profound cavities in the bottom of the sea, but its mean depth probably does not much exceed the mean height of the continents and islands above its level. On this account, immense tracts of land may be deserted or overwhelmed by the ocean, as appears really to have been the case, without any great change in the form of the terrestrial spheroid. The variation in the length of the pendulum was first remarked by Richter in 1672, while observing transits of the fixed stars across the meridian at Cayenne, about five degrees north of the equator. He found that his clock lost at the rate of 2m 28s daily, which induced him to determine the length of a pendulum beating seconds in that latitude; and, repeating the experiments on his return to Europe, he found the seconds’ pendulum at Paris to be more than the twelfth of an inch longer than that at Cayenne. The form and size of the earth being determined, a standard of measure is furnished with which the dimensions of the solar system may be compared.
Parallax—Lunar Parallax found from Direct Observation—Solar Parallax deduced from the Transit of Venus—Distance of the Sun from the Earth—Annual Parallax—Distance of the Fixed Stars.
The parallax of a celestial body is the angle under which the radius of the earth would be seen if viewed from the centre of that body; it affords the means of ascertaining the distances of the sun, moon, and planets (N. 130). When the moon is in the horizon at the instant of rising or setting, suppose lines to be drawn from her centre to the spectator and to the centre of the earth: these would form a right-angled triangle with the terrestrial radius, which is of a known length; and, as the parallax or angle at the moon can be measured, all the angles and one side are given; whence the distance of the moon from the centre of the earth may be computed. The parallax of an object may be found, if two observers under the same meridian, but at a very great distance from one another, observe its zenith distances on the same day at the time of its passage over the meridian. By such contemporaneous observations at the Cape of Good Hope and at Berlin, the mean horizontal parallax of the moon was found to be 3459ʺ, whence the mean distance of the moon is about sixty times the greatest terrestrial radius, or 237,608 miles nearly.[4] Since the parallax is equal to the radius of the earth divided by the distance of the moon, it varies with the distance of the moon from the earth under the same parallel of latitude, and proves the ellipticity of the lunar orbit. When the moon is at her mean distance, it varies with the terrestrial radii, thus showing that the earth is not a sphere (N. 131).
Although the method described is sufficiently accurate for finding the parallax of an object as near as the moon, it will not answer for the sun, which is so remote that the smallest error in observation would lead to a false result. But that difficulty is obviated by the transits of Venus. When that planet is in her nodes (N. 132), or within 11⁄4° of them, that is, in, or nearly in, the plane of the ecliptic, she is occasionally seen to pass over the 53sun like a black spot. If we could imagine that the sun and Venus had no parallax, the line described by the planet on his disc, and the duration of the transit, would be the same to all the inhabitants of the earth. But, as the semi-diameter of the earth has a sensible magnitude when viewed from the centre of the sun, the line described by the planet in its passage over his disc appears to be nearer to his centre, or farther from it, according to the position of the observer; so that the duration of the transit varies with the different points of the earth’s surface at which it is observed (N. 133). This difference of time, being entirely the effect of parallax, furnishes the means of computing it from the known motions of the earth and Venus, by the same method as for the eclipses of the sun. In fact, the ratio of the distances of Venus and the sun from the earth at the time of the transit is known from the theory of their elliptical motion. Consequently the ratio of the parallaxes of these two bodies, being inversely as their distances, is given; and as the transit gives the difference of the parallaxes, that of the sun is obtained. In 1769 the parallax of the sun was determined by observations of a transit of Venus made at Wardhus in Lapland, and at Tahiti in the South Sea. The latter observation was the object of Cook’s first voyage. The transit lasted about six hours at Tahiti, and the difference in duration at these two stations was eight minutes; whence the sun’s horizontal parallax was found to be 8ʺ·72. But by other considerations it has been reduced by Professor Encke to 8ʺ·5776; from which the mean distance of the sun appears to be about ninety-five millions of miles. This is confirmed by an inequality in the motion of the moon, which depends upon the parallax of the sun, and which, when compared with observation, gives 8ʺ·6 for the sun’s parallax. The transits of Venus in 1874 and 1882 will be unfavourable for ascertaining the accuracy of the solar parallax, and no other transit of that planet will take place till the twenty-first century; but in the mean time recourse may be had to the oppositions of Mars.
The parallax of Venus is determined by her transits; that of Mars by direct observation, and it is found to be nearly double that of the sun, when the planet is in opposition. The distance of these two planets from the earth is therefore known in terrestrial radii, consequently their mean distances from the sun may be computed; and as the ratios of the distances of the planets from the sun are known by Kepler’s law, of the squares 54of the periodic times of any two planets being as the cubes of their mean distances from the sun, their absolute distances in miles are easily found (N. 134). This law is very remarkable, in thus uniting all the bodies of the system, and extending to the satellites as well as the planets.
Far as the earth seems to be from the sun, Uranus is no less than nineteen, and Neptune thirty times farther. Situate on the verge of the system, the sun must appear from Uranus not much larger than Venus does to us, and from Neptune as a star of the fifth magnitude. The earth cannot even be visible as a telescopic object to a body so remote as either Uranus or Neptune. Yet man, the inhabitant of the earth, soars beyond the vast dimensions of the system to which his planet belongs, and assumes the diameter of its orbit as the base of a triangle whose apex extends to the stars.
Sublime as the idea is, this assumption proves ineffectual, except in a very few cases; for the apparent places of the fixed stars are not sensibly changed by the earth’s annual revolution. With the aid derived from the refinements of modern astronomy, and of the most perfect instruments, a sensible parallax has been detected only in a very few of these remote suns. α Centauri has a parallax of one second of space, therefore it is the nearest known star, and yet it is more than two hundred thousand times farther from us than the sun is. At such a distance not only the terrestrial orbit shrinks to a point, but the whole solar system, seen in the focus of the most powerful telescope, might be eclipsed by the thickness of a spider’s thread. Light, flying at the rate of 190,000 miles in a second, would take more than three years to travel over that space. One of the nearest stars may therefore have been kindled or extinguished more than three years before we could have been aware of so mighty an event. But this distance must be small when compared with that of the most remote of the bodies which are visible in the heavens. The fixed stars are undoubtedly luminous like the sun: it is therefore probable that they are not nearer to one another than the sun is to the nearest of them. In the milky way and the other starry nebulæ, some of the stars that seem to us to be close to others may be far behind them in the boundless depth of space; nay, may be rationally supposed to be situate many thousand times farther off. Light would therefore require thousands of years to come to the earth from those myriads of suns of which our own is but “the remote companion.”
Masses of Planets that have no Satellites determined from their Perturbations—Masses of the others obtained from the Motions of their Satellites—Masses of the Sun, the Earth, of Jupiter and of the Jovial System—Mass of the Moon—Real Diameters of Planets, how obtained—Size of Sun, Densities of the Heavenly Bodies—Formation of Astronomical Tables—Requisite Data and Means of obtaining them.
The masses of such planets as have no satellites are known by comparing the inequalities they produce in the motions of the earth and of each other, determined theoretically, with the same inequalities given by observation; for the disturbing cause must necessarily be proportional to the effect it produces. The masses of the satellites themselves may also be compared with that of the sun by their perturbations. Thus, it is found, from the comparison of a vast number of observations with La Place’s theory of Jupiter’s satellites, that the mass of the sun is no less than 65,000,000 times greater than the least of these moons. But, as the quantities of matter in any two primary planets are directly as the cubes of the mean distances at which their satellites revolve, and inversely as the squares of their periodic times (N. 135), the mass of the sun and of any planets which have satellites may be compared with the mass of the earth. In this manner it is computed that the mass of the sun is 354,936 times that of the earth; whence the great perturbations of the moon, and the rapid motion of the perigee and nodes of her orbit (N. 136). Even Jupiter, the largest of the planets, has been found by Professor Airy to be 1047·871 times less than the sun; and, indeed, the mass of the whole Jovial system is not more than the 1054·4th part of that of the sun. So that the mass of the satellites bears a very small proportion to that of their primary. The mass of the moon is determined from several sources—from her action on the terrestrial equator, which occasions the nutation in the axis of rotation; from her horizontal parallax; from an inequality she produces in the sun’s longitude; and from her action on the tides. The three first quantities, computed from 56theory and compared with their observed values, give her mass respectively equal to the 1⁄71, 1⁄74·2, and 1⁄69·2, part of that of the earth, which do not differ much from each other. Dr. Brinkley has found it to be 1⁄80 from the constant of lunar nutation: but, from the moon’s action in raising the tides, her mass appears to be about the 1⁄75 part of that of the earth—a value that cannot differ much from the truth.
The apparent diameters of the sun, moon, and planets are determined by measurement; therefore their real diameters may be compared with that of the earth; for the real diameter of a planet is to the real diameter of the earth, or 7926 miles, as the apparent diameter of the planet to the apparent diameter of the earth as seen from the planet, that is, to twice the parallax of the planet. According to Bessel, the mean apparent diameter of the sun is 1923ʺ·64, and with the solar parallax 8ʺ·5776, it will be found that the diameter of the sun is about 886,877 miles. Therefore, if the centre of the sun were to coincide with the centre of the earth, his volume would not only include the orbit of the moon, but would extend nearly as far again; for the moon’s mean distance from the earth is about sixty times the earth’s equatorial radius, or 238,793 miles: so that twice the distance of the moon is 477,586 miles, which differs but little from the solar radius; his equatorial radius is probably not much less than the major axis of the lunar orbit. The diameter of the moon is only 2160 miles; and Jupiter’s diameter of 88,200 miles is very much less than that of the sun; the diameter of Pallas does not much exceed 79 miles, so that an inhabitant of that planet, in one of our steam carriages, might go round his world in a few hours. The diameters of Lutetia and Atalanta are only 8 and 4 miles respectively; but the whole of the 55 telescopic planets are so small, that their united mass is probably not more than the fifth or sixth part of that of the moon.
The densities of bodies are proportional to their masses, divided by their volumes. Hence, if the sun and planets be assumed to be spheres, their volumes will be as the cubes of their diameters. Now, the apparent diameters of the sun and earth, at their mean distance, are 1923ʺ·6 and 17ʺ·1552, and the mass of the earth is the 354,936th part of that of the sun taken as the unit. It follows, therefore, that the earth is four times as dense as the sun. But the sun is so large that his attractive force would 57cause bodies to fall through about 334·65 feet in a second. Consequently, if he were habitable by human beings, they would be unable to move, since their weight would be thirty times as great as it is here. A man of moderate size would weigh about two tons at the surface of the sun; whereas at the surface of some of the new planets he would be so light that it would be impossible to stand steady, since he would only weigh a few pounds. The mean density of the earth has been determined by the following method. Since a comparison of the action of two planets upon a third gives the ratio of the masses of these two planets, it is clear that, if we can compare the effect of the whole earth with the effect of any part of it, a comparison may be instituted between the mass of the whole earth and the mass of that part of it. Now a leaden ball was weighed against the earth by comparing the effects of each upon a pendulum; the nearness of the smaller mass making it produce a sensible effect as compared with that of the larger: for by the laws of attraction the whole earth must be considered as collected in its centre. By this method it has been found that the mean density of the earth is 5·660 times greater than that of water at the temperature of 62° of Fahrenheit’s thermometer. The late Mr. Baily, whose accuracy as an experimental philosopher is acknowledged, was unremittingly occupied nearly four years in accomplishing this very important object. In order to ascertain the mean density of the earth still more perfectly, Mr. Airy made a series of experiments to compare the simultaneous oscillations of two pendulums, one at the bottom of the Harton coal-pit, 1260 feet deep, in Northumberland, and the other on the surface of the earth immediately above it. The oscillations of the pendulums were compared with an astronomical clock at each station, and the time was instantaneously transmitted from one to the other by a telegraphic wire. The oscillations were observed for more than 100 hours continuously, when it was found that the lower pendulum made 21⁄2 oscillations more in 24 hours than the upper one. The experiment was repeated for the same length of time with the same result; but on this occasion the upper pendulum was taken to the bottom of the mine and the lower brought to the surface. From the difference between the oscillations at the two stations it appears that gravitation at the bottom of the mine exceeds that at the surface by the 1⁄19190 part, and that the 58mean density of the earth is 6·565, which is greater than that obtained by Mr. Baily by ·89. While employed on the trigonometrical survey of Scotland, Colonel James determined the mean density of the earth to be 5·316, from a deviation of the plumb-line amounting to 2ʺ, caused by the attraction of Arthur’s Seat and the heights east of Edinburgh: it agrees more nearly with the density found by Mr. Baily than with that deduced from Mr. Airy’s experiments. All the planets and satellites appear to be of less density than the earth. The motions of Jupiter’s satellites show that his density increases towards his centre. Were his mass homogeneous, his equatorial and polar axes would be in the ratio of 41 to 36, whereas they are observed to be only as 41 to 38. The singular irregularities in the form of Saturn, and the great compression of Mars, prove the internal structure of these two planets to be very far from uniform.
Before entering on the theory of rotation, it may not be foreign to the subject to give some idea of the methods of computing the places of the planets, and of forming astronomical tables. Astronomy is now divided into the three distinct departments of theory, observation, and computation. Since the problem of the three bodies can only be solved by approximation, the analytical astronomer determines the position of a planet in space by a series of corrections. Its place in its circular orbit is first found, then the addition or subtraction of the equation of the centre (N. 48) to or from its mean place gives its position in the ellipse. This again is corrected by the application of the principal periodic inequalities. But, as these are determined for some particular position of the three bodies, they require to be corrected to suit other relative positions. This process is continued till the corrections become less than the errors of observation, when it is obviously unnecessary to carry the approximation further. The true latitude and distance of the planet from the sun are obtained by methods similar to those employed for the longitude.
As the earth revolves equably about its axis in 24 hours, at the rate of 15° in an hour, time becomes a measure of angular motion, and the principal element in astronomy, where the object is to determine the exact state of the heavens and the successive changes it undergoes in all ages, past, present, and to come. Now, the longitude, latitude, and distance of a planet from the 59sun are given in terms of the time, by general analytical formulæ. These formulæ will consequently give the exact place of the body in the heavens, for any time assumed at pleasure, provided they can be reduced to numbers. But before the calculator begins his task the observer must furnish the necessary data, which are, obviously, the forms of the orbits, and their positions with regard to the plane of the ecliptic (N. 57). It is therefore necessary to determine by observation, for each planet, the length of the major axis of its orbit, the excentricity, the inclination of the orbit to the plane of the ecliptic, the longitudes of its perihelion and ascending node at a given time, the periodic time of the planet, and its longitude at any instant arbitrarily assumed, as an origin from whence all its subsequent and antecedent longitudes are estimated. Each of these quantities is determined from that position of the planet on which it has most influence. For example, the sum of the greatest and least distances of the planet from the sun is equal to the major axis of the orbit, and their difference is equal to twice the excentricity. The longitude of the planet, when at its least distance from the sun, is the same with the longitude of the perihelion; the greatest latitude of the planet is equal to the inclination of the orbit: the longitude of the planet, when in the plane of the ecliptic in passing towards the north, is the longitude of the ascending node, and the periodic time is the interval between two consecutive passages of the planet through the same node, a small correction being made for the precession of the node during the revolution of the planet (N. 137). Notwithstanding the excellence of instruments and the accuracy of modern observers, unavoidable errors of observation can only be compensated by finding the value of each element from the mean of a thousand, or even many thousands of observations. For as it is probable that the errors are not all in one direction, but that some are in excess and others in defect, they will compensate each other when combined.
However, the values of the elements determined separately can only be regarded as approximate, because they are so connected that the estimation of any one independently will induce errors in the others. The excentricity depends upon the longitude of the perihelion, the mean motion depends upon the major axis, the longitude of the node upon the inclination of the orbit, and vice versâ. Consequently, the place of a planet computed 60with the approximate data will differ from its observed place. Then the difficulty is to ascertain what elements are most in fault, since the difference in question is the error of all; that is obviated by finding the errors of some thousands of observations, and combining them, so as to correct the elements simultaneously, and to make the sum of the squares of the errors a minimum with regard to each element (N. 138). The method of accomplishing this depends upon the Theory of Probabilities; a subject fertile in most important results in the various departments of science and of civil life, and quite indispensable in the determination of astronomical data. A series of observations continued for some years will give approximate values of the secular and periodic inequalities, which must be corrected from time to time, till theory and observation agree. And these again will give values of the masses of the bodies forming the solar system, which are important data in computing their motions. The periodic inequalities derived from a great number of observations are employed for the determination of the values of the masses till such time as the secular inequalities shall be perfectly known, which will then give them with all the necessary precision. When all these quantities are determined in numbers, the longitude, latitude, and distance of the planet from the sun are computed for stated intervals, and formed into tables, arranged according to the time estimated from a given epoch, so that the place of the body may be determined from them by inspection alone, at any instant for perhaps a thousand years before and after that epoch. By this tedious process, tables have been computed for all the great planets, and several of the small, besides the moon and the satellites of Jupiter. In the present state of astronomy the masses and elements of the orbits are pretty well known, so that the tables only require to be corrected from time to time as observations become more accurate. Those containing the motions of Jupiter, Saturn, and Uranus have already been twice constructed within the last thirty years, and the tables of Jupiter and Saturn agree almost perfectly with modern observation. The following prediction will be found in the sixth edition of this book, published in the year 1842: “Those of Uranus, however, are already defective, probably because the discovery of that planet in 1781 is too recent to admit of much precision in the determination of 61its motions, or that possibly it may be subject to disturbances from some unseen planet revolving about the sun beyond the present boundaries of our system. If, after a lapse of years, the tables formed from a combination of numerous observations should be still inadequate to represent the motions of Uranus, the discrepancies may reveal the existence, nay, even the mass and orbit, of a body placed for ever beyond the sphere of vision.”[5]
That prediction has been fulfilled since the seventh edition of this book was published. Not only the existence of Neptune, revolving at the distance of three thousand millions of miles from the sun, has been discovered from his disturbing action on Uranus, but his mass, the form and position of his orbit in space, and his periodic time had been determined before the planet had been seen, and the planet itself was discovered in the very point of the heavens which had been assigned to it. It had been noticed for years that the perturbation of Uranus had increased in an unaccountable manner (N. 139). After the disturbing action of all the known planets had been determined, it was found that, between the years 1833 and 1837, the observed and computed distance of Uranus from the sun differed by 240,000 miles, which is about the mean distance of the moon from the earth, while, in 1841, the error in the geocentric longitude of the planet amounted to 96ʺ. These discrepancies were therefore attributed to the attraction of some unseen and unknown planet, consequently they gave rise to a case altogether unprecedented in the history of astronomy. Heretofore it was required to determine the disturbing action of one known planet upon another. Whereas the inverse problem had now to be solved, in which it was required to find the place of an unknown body in the heavens, at a given time, together with its mass, and the form and position of its orbit, from the disturbance it produced on the motions of another. The difficulty was extreme, because all the elements of the orbit of Uranus were erroneous from the action of Neptune, and those of Neptune’s orbit were unknown. In this dilemma it was necessary to form some hypothesis with regard to the unknown planet; it was therefore assumed, according to Bode’s empirical law on the mean distances of the planets, that it was revolving at twice the distance of Uranus from the sun. 62In fact, the periodic time of Uranus is about 84 years, and, as the discrepancies in his motions increased slowly and regularly, it was evident that it would require a planet with a much longer periodic time to produce them—moreover, it was clear that the new planet must be exterior to Uranus, otherwise it would have disturbed the motions of Saturn.
Another circumstance tended to lessen the difficulty; the latitude of Uranus was not much affected, therefore it was concluded that the inclination of the orbit of the unknown body must be very small, and, as that of the orbit of Uranus is only 46ʹ 28ʺ·4, both planets were assumed to be moving in the plane of the ecliptic, and thus the elements of the orbit of the unknown planet were reduced from six to four. Having thus assumed that the unknown body was revolving in a circle in the plane of the ecliptic, the analytical expression of its action on the motion of Uranus, when in numerous points of its orbit, was compared with the observed longitude of Uranus, through a regular series of years, by means of which the faulty elements of the orbit of Uranus were eliminated, or got rid of, and there only remained a relation between the mass of the new planet and three of the elements of its orbit; and it then was necessary to assume such a value for two of them as would suit the rest. That was accomplished so dexterously, that the perturbations of Uranus were perfectly conformable to the motions of Neptune, moving in the orbit thus found, and the place of the new planet exactly agreed with observation. Subsequently its orbit and motions have been determined more accurately.
The honour of this admirable effort of genius is shared by Mr. Adams and M. Le Verrier, who, independently of each other, arrived at these wonderful results. Mr. Adams had determined the mass and apparent diameter of Neptune, with all the circumstances of its motion, eight months before M. Le Verrier had terminated his results, and had also pointed out the exact spot where the planet would be found; but the English observers neglected to look for it till M. Le Verrier made known his researches, and communicated its position to Dr. Galle, at Berlin, who found it the very first night he looked for it, and then it was evident that it would have been seen in the place Mr. Adams had assigned to it eight months before had it been looked for. So closely did the results of these two great mathematicians agree.
63Neptune has a diameter of 39,793 miles, consequently he is nearly 200 times larger than the earth, and may be seen with a telescope of moderate power. His motion is retrograde at present, and six times slower than that of the earth. At so great a distance from the sun it can only have the 1⁄1300th part of the light and heat the earth receives; but having a satellite, the deficiency of light may in some measure be supplied.
The prediction may now be transferred from Uranus to Neptune, whose perturbations may reveal the existence of a planet still further removed, which may for ever remain beyond the reach of telescopic vision—yet its mass, the form and position of its orbit, and all the circumstances of its motion may become known, and the limits of the solar system may still be extended hundreds of millions of miles.
The mean distance of Neptune from the sun has subsequently proved to be only 2893 millions of miles, and the period of his revolution 166 years, so that Baron Bode’s law, of the interval between the orbits of any two planets being twice as great as the inferior interval and half of the superior, fails in the case of Neptune, though it was useful on the first approximation to his motions; and since Bode’s time it has led to the discovery of fifty-five telescopic planets revolving between the orbits of Mars and Jupiter, some by chance, others by a systematic search on the faith that these minute planets are fragments of a larger body that has exploded, because their distances from the sun are nearly the same; the lines of the nodes of some of their orbits terminate in the same points of the heavens, and the inclinations of their orbits are such as might have taken place from their mutual disturbances at the time of the explosion, and while yet they were near enough for their forms to affect their motions. The orbits of the more recently discovered asteroids show that this hypothesis is untenable.
The tables of Mars, Venus, and even those of the sun, have been greatly improved, and still engage the attention of our Astronomer Royal, Mr. Airy, and other eminent astronomers. We are chiefly indebted to the German astronomers for tables of the four older telescopic planets, Vesta, Juno, Ceres, and Pallas; the others have only been discovered since the year 1845.
The determination of the path of a planet when disturbed by all the others, a problem which has employed the talents of the 64greatest astronomers, from Newton to the present day, is only successfully accomplished with regard to the older planets, which revolve in nearly circular orbits, but little inclined to the plane of the ecliptic. When the excentricity and inclination of the orbits are great, their analysis fails, because the series expressing the co-ordinates of the bodies become extremely complicated, and do not converge when applied to comets and the telescopic planets. This difficulty has been overcome by Sir John Lubbock, and other mathematicians, who have the honour of having completed the theory of planetary motion, which becomes every day of more importance, from the new planets that have been discovered, and also with regard to comets, many of which return to the sun at regular intervals, and from whose perturbations the masses of the planets will be more accurately determined, and the retarding influence of the ethereal medium better known.
Rotation of the Sun and Planets—Saturn’s Rings—Periods of the Rotation of the Moon and other Satellites equal to the Periods of their Revolutions—Form of Lunar Spheroid—Libration, Aspect, and Constitution of the Moon—Rotation of Jupiter’s Satellites.
The oblate form of several of the planets indicates rotatory motion. This has been confirmed in most cases by tracing spots on their surface, by which their poles and times of rotation have been determined. The rotation of Mercury is unknown, on account of his proximity to the sun; that of the new planets has not yet been ascertained. The sun revolves in twenty-five days and ten hours about an axis which is directed towards a point half-way between the pole-star and α of Lyra, the plane of rotation being inclined by 7° 30ʹ, or a little more than seven degrees, to the plane of the ecliptic: it may therefore be concluded that the sun’s mass is a spheroid, flattened at the poles. From the rotation of the sun, there was every reason to believe that he has a progressive motion in space, a circumstance which is confirmed by observation. But, in consequence of the reaction of the planets, he describes a small irregular orbit about the centre of gravity of the system, never deviating from his position by more than twice his own diameter, or a little more than seven times the distance of the moon from the earth. The sun and all his attendants rotate from west to east, on axes that remain nearly parallel to themselves (N. 140) in every point of their orbit, and with angular velocities that are sensibly uniform (N. 141). Although the uniformity in the direction of their rotation is a circumstance hitherto unaccounted for in the economy of nature, yet, from the design and adaptation of every other part to the perfection of the whole, a coincidence so remarkable cannot be accidental. And, as the revolutions of the planets and satellites are also from west to east, it is evident that both must have arisen from the primitive cause which determined the planetary motions.[6] Indeed, La Place has computed the probability to be 66as four millions to one that all the motions of the planets, both of rotation and revolution, were at once imparted by an original common cause, but of which we know neither the nature nor the epoch.
The larger planets rotate in shorter periods than the smaller planets and the earth. Their compression is consequently greater, and the action of the sun and of their satellites occasions a nutation in their axes and a precession of their equinoxes (N. 147) similar to that which obtains in the terrestrial spheroid, from the attraction of the sun and moon on the prominent matter at the equator. Jupiter revolves in less than ten hours round an axis at right angles to certain dark belts or bands, which always cross his equator. (See Plate 1.) This rapid rotation occasions a very great compression in his form. His equatorial axis exceeds his polar axis by 6000 miles, whereas the difference in the axes of the earth is only about twenty-six and a half. It is an evident consequence of Kepler’s law of the squares of the periodic times of the planets being as the cubes of the major axes of their orbits, that the heavenly bodies move slower the farther they are from the sun. In comparing the periods of the revolutions of Jupiter and Saturn with the times of their rotation, it appears that a year of Jupiter contains nearly ten thousand of his days, and that of Saturn about thirty thousand Saturnian days.
The appearance of Saturn is unparalleled in the system of the world. He is a spheroid nearly 1000 times larger than the earth, surrounded by a ring even brighter than himself, which always remains suspended in the plane of his equator: and, viewed with a very good telescope, it is found to consist of two concentric rings, divided by a dark band. The exterior ring, as seen through Mr. Lassell’s great equatorial at Malta, has a dark-striped band through the centre, and is altogether less bright than the interior ring, one half of which is extremely brilliant; while the interior half is shaded in rings like the seats in an amphitheatre. Mr. Lassell made the remarkable discovery of a dark transparent ring, whose edge coincides with the inner edge of the interior ring, and which occupies about half the space between it and Saturn. He compares it to a band of dark-coloured crape drawn across a portion of the disc of the planet, and the part projected upon the blue sky is also transparent. At the time these observations were made at Malta, Captain Jacob discovered the transparent ring at Madras. It is conjectured to be 67fluid; even the luminous rings cannot be very dense, since the density of Saturn himself is known to be less than the eighth part of that of the earth. A transit of the ring across a star might reveal something concerning this wonderful object. The ball of Saturn is striped by belts of different colours. At the time of these observations the part above the ring was bright white; at his equator there was a ruddy belt divided in two, above which were belts of a bluish green alternately dark and light, while at the pole there was a circular space of a pale colour. (See Plate 2.) The mean distance of the interior part of the double ring from the surface of the planet is about 22,240 miles, it is no less than 33,360 miles broad, but, by the estimation of Sir John Herschel, its thickness does not much exceed 100 miles, so that it appears like a plane. By the laws of mechanics, it is impossible that this body can retain its position by the adhesion of its particles alone. It must necessarily revolve with a velocity that will generate a centrifugal force sufficient to balance the attraction of Saturn. Observation confirms the truth of these principles, showing that the rings rotate from west to east about the planet in ten hours and a half, which is nearly the time a satellite would take to revolve about Saturn at the same distance. Their plane is inclined to the ecliptic, at an angle of 28° 10ʹ 44ʺ·5; in consequence of this obliquity of position, they always appear elliptical to us, but with an excentricity so variable as even to be occasionally like a straight line drawn across the planet. In the beginning of October, 1832, the plane of the rings passed through the centre of the earth; in that position they are only visible with very superior instruments, and appear like a fine line across the disc of Saturn. About the middle of December, in the same year, the rings became invisible, with ordinary instruments, on account of their plane passing through the sun. In the end of April, 1833, the rings vanished a second time, and reappeared in June of that year. Similar phenomena will occur as often as Saturn has the same longitude with either node of his rings. Each side of these rings has alternately fifteen years of sunshine and fifteen years of darkness.
It is a singular result of theory, that the rings could not maintain their stability of rotation if they were everywhere of uniform thickness; for the smallest disturbance would destroy the equilibrium, which would become more and more deranged, 68till, at last, they would be precipitated on the surface of the planet. The rings of Saturn must therefore be irregular solids, of unequal breadth in different parts of the circumference, so that their centres of gravity do not coincide with the centres of their figures. Professor Struve has also discovered that the centre of the rings is not concentric with the centre of Saturn. The interval between the outer edge of the globe of the planet and the outer edge of the rings on one side is 11ʺ·272, and, on the other side, the interval is 11ʺ·390, consequently there is an excentricity of the globe in the rings of 0ʺ·215. If the rings obeyed different forces, they would not remain in the same plane, but the powerful attraction of Saturn always maintains them and his satellites in the plane of his equator. The rings, by their mutual action, and that of the sun and satellites, must oscillate about the centre of Saturn, and produce phenomena of light and shadow whose periods extend to many years. According to M. Bessel the mass of Saturn’s ring is equal to the 1⁄118 part of that of the planet.
The periods of rotation of the moon and the other satellites are equal to the times of their revolutions, consequently these bodies always turn the same face to their primaries. However, as the mean motion of the moon is subject to a secular inequality, which will ultimately amount to many circumferences (N. 108), if the rotation of the moon were perfectly uniform and not affected by the same inequalities, it would cease exactly to counterbalance the motion of revolution; and the moon, in the course of ages, would successively and gradually discover every point of her surface to the earth. But theory proves that this never can happen; for the rotation of the moon, though it does not partake of the periodic inequalities of her revolution, is affected by the same secular variations, so that her motions of rotation and revolution round the earth will always balance each other, and remain equal. This circumstance arises from the form of the lunar spheroid, which has three principal axes of different lengths at right angles to each other.
The moon is flattened at her poles from her centrifugal force, therefore her polar axis is the least. The other two are in the plane of her equator, but that directed towards the earth is the greatest (N. 142). The attraction of the earth, as if it had drawn out that part of the moon’s equator, constantly brings the 69greatest axis, and consequently the same hemisphere, towards us, which makes her rotation participate in the secular variations of her mean motion of revolution. Even if the angular velocities of rotation and revolution had not been nicely balanced in the beginning of the moon’s motion, the attraction of the earth would have recalled the greatest axis to the direction of the line joining the centres of the moon and earth; so that it would have vibrated on each side of that line in the same manner as a pendulum oscillates on each side of the vertical from the influence of gravitation. No such libration is perceptible; and, as the smallest disturbance would make it evident, it is clear that, if the moon has ever been touched by a comet, the mass of the latter must have been extremely small. If it had been only the hundred thousandth part of that of the earth, it would have rendered the libration sensible. According to analysis, a similar libration exists in the motions of Jupiter’s satellites, which still remains insensible to observation, and yet the comet of 1770 passed twice through the midst of them.
The moon, it is true, is liable to librations depending upon the position of the spectator. At her rising, part of the western edge of her disc is visible, which is invisible at her setting, and the contrary takes place with regard to her eastern edge. There are also librations arising from the relative positions of the earth and moon in their respective orbits; but, as they are only optical appearances, one hemisphere will be eternally concealed from the earth. For the same reason the earth, which must be so splendid an object to one lunar hemisphere, will be for ever veiled from the other. On account of these circumstances, the remoter hemisphere of the moon has its day a fortnight long, and a night of the same duration, not even enlightened by a moon, while the favoured side is illuminated by the reflection of the earth during its long night. A planet exhibiting a surface thirteen times larger than that of the moon, with all the varieties of clouds, land, and water, coming successively into view, must be a splendid object to a lunar traveller in a journey to his antipodes. The great height of the lunar mountains probably has a considerable influence on the phenomena of her motion, the more so as her compression is small, and her mass considerable. In the curve passing through the poles, and that diameter of the moon which always points to the earth, nature has furnished a permanent 70meridian, to which the different spots on her surface have been referred, and their positions are determined with as much accuracy as those of many of the most remarkable places on the surface of our globe. According to the observations of Professor Secchi at Rome, the mountains of the moon are mostly volcanic and of three kinds. The first and oldest have their borders obliterated, so that they look like deep wells; the second, which are of an intermediate class, have elevated, and, for the most part, regular unbroken edges, with the ground around them raised to a prodigious extent in proportion to the size of the volcano, with generally an insulated rock in the centre of the crater. The third, and most recent class, are very small, and seem to be the last effort of the expiring volcanic force, which is probably now extinct.
The distance and minuteness of Jupiter’s satellites render it extremely difficult to ascertain their rotation. It was, however, accomplished by Sir William Herschel from their relative brightness. He observed that they alternately exceed each other in brilliancy, and, by comparing the maxima and minima of their illumination with their positions relatively to the sun and to their primary, he found that, like the moon, the time of their rotation is equal to the period of their revolution about Jupiter. Miraldi was led to the same conclusion with regard to the fourth satellite, from the motion of a spot on its surface.
Rotation of the Earth invariable—Decrease in the Earth’s mean Temperature—Earth originally in a state of Fusion—Length of Day constant—Decrease of Temperature ascribed by Sir John Herschel to the variation in the Excentricity of the Terrestrial Orbit—Difference in the Temperature of the two Hemispheres erroneously ascribed to the Excess in the Length of Spring and Summer in the Southern Hemisphere; attributed by Sir Charles Lyell to the Operation of existing Causes—Three principal Axes of Rotation—Position of the Axis of Rotation on the Surface of the Earth invariable—Ocean not sufficient to restore the Equilibrium of the Earth if deranged—Its Density and mean Depth—Internal Structure of the Earth.
The rotation of the earth, which determines the length of the day, may be regarded as one of the most important elements in the system of the world. It serves as a measure of time, and forms the standard of comparison for the revolutions of the celestial bodies, which, by their proportional increase or decrease, would soon disclose any changes it might sustain. Theory and observation concur in proving that, among the innumerable vicissitudes which prevail throughout creation, the period of the earth’s diurnal rotation is immutable. The water of rivers, falling from a higher to a lower level, carries with it the velocity due to its revolution with the earth at a greater distance from the centre; it will therefore accelerate, although to an almost infinitesimal extent, the earth’s daily rotation. The sum of all these increments of velocity, arising from the descent of all the rivers on the earth’s surface, would in time become perceptible, did not nature, by the process of evaporation, raise the waters back to their sources, and thus, by again removing matter to a greater distance from the centre, destroy the velocity generated by its previous approach; so that the descent of rivers does not affect the earth’s rotation. Enormous masses projected by volcanoes from the equator to the poles, and the contrary, would indeed affect it, but there is no evidence of such convulsions. The disturbing action of the moon and planets, which has so powerful an effect on the revolution of the earth, in no way 72influences its rotation. The constant friction of the trade winds on the mountains and continents between the tropics does not impede its velocity, which theory even proves to be the same as if the sea, together with the earth, formed one solid mass. But, although these circumstances be insufficient, a variation in the mean temperature would certainly occasion a corresponding change in the velocity of rotation. In the science of dynamics it is a principle in a system of bodies or of particles revolving about a fixed centre, that the momentum or sum of the products of the mass of each into its angular velocity and distance from the centre is a constant quantity, if the system be not deranged by a foreign cause. Now, since the number of particles in the system is the same whatever its temperature may be, when their distances from the centre are diminished, their angular velocity must be increased, in order that the preceding quantity may still remain constant. It follows, then, that, as the primitive momentum of rotation with which the earth was projected into space must necessarily remain the same, the smallest decrease in heat, by contracting the terrestrial spheroid, would accelerate its rotation, and consequently diminish the length of the day. Notwithstanding the constant accession of heat from the sun’s rays, geologists have been induced to believe, from the fossil remains, that the mean temperature of the globe is decreasing.
The high temperature of mines, hot springs, and above all the internal fires which have produced, and do still occasion, such devastation on our planet, indicate an augmentation of heat towards its centre. The increase of density corresponding to the depth and the form of the spheroid, being what theory assigns to a fluid mass in rotation, concurs to induce the idea that the temperature of the earth was originally so high as to reduce all the substances of which it is composed to a state of fusion or of vapour, and that in the course of ages it has cooled down to its present state; that it is still becoming colder; and that it will continue to do so till the whole mass arrives at the temperature of the medium in which it is placed, or rather at a state of equilibrium between this temperature, the cooling power of its own radiation, and the heating effect of the sun’s rays.
Previous to the formation of ice at the poles, the ancient lands of northern latitudes might, no doubt, have been capable of producing those tropical plants preserved in the coal-measures, if 73indeed such plants could flourish without the intense light of a tropical sun. But, even if the decreasing temperature of the earth be sufficient to produce the observed effects, it must be extremely slow in its operation; for, in consequence of the rotation of the earth being a measure of the periods of the celestial motions, it has been proved that, if the length of the day had decreased by the three-thousandth part of a second since the observations of Hipparchus two thousand years ago, it would have diminished the secular equation of the moon by 44ʺ·4. It is, therefore, beyond a doubt that the mean temperature of the earth cannot have sensibly varied during that time. If, then, the appearances exhibited by the strata are really owing to a decrease of internal temperature, it either shows the immense periods requisite to produce geological changes, to which two thousand years are as nothing, or that the mean temperature of the earth had arrived at a state of equilibrium before these observations.
However strong the indications of the primitive fluidity of the earth, as there is no direct proof of it, the hypothesis can only be regarded as very probable. But one of the most profound philosophers and elegant writers of modern times has found in the secular variation of the excentricity of the terrestrial orbit an evident cause of decreasing temperature. That accomplished author, in pointing out the mutual dependencies of phenomena, says, “It is evident that the mean temperature of the whole surface of the globe, in so far as it is maintained by the action of the sun at a higher degree than it would have were the sun extinguished, must depend on the mean quantity of the sun’s rays which it receives, or—which comes to the same thing—on the total quantity received in a given invariable time; and, the length of the year being unchangeable in all the fluctuations of the planetary system, it follows that the total amount of solar radiation will determine, cæteris paribus, the general climate of the earth. Now, it is not difficult to show that this amount is inversely proportional to the minor axis of the ellipse described by the earth about the sun (N. 143), regarded as slowly variable; and that, therefore, the major axis remaining, as we know it to be, constant, and the orbit being actually in a state of approach to a circle, and consequently the minor axis being on the increase, the mean annual amount of solar radiation received 74by the whole earth must be actually on the decrease. We have, therefore, an evident real cause to account for the phenomenon.” The limits of the variation in the excentricity of the earth’s orbit are unknown. But, if its ellipticity has ever been as great as that of the orbit of Mercury or Pallas, the mean temperature of the earth must have been sensibly higher than it is at present. Whether it was great enough to render our northern climates fit for the production of tropical plants, and for the residence of the elephant and other animals now inhabitants of the torrid zone, it is impossible to say.
Of the decrease in temperature of the northern hemisphere there is abundant evidence in the fossil plants discovered in very high latitudes, which could only have existed in a tropical climate, and which must have grown near the spot where they are found, from the delicacy of their structure and the perfect state of their preservation. This change of temperature has been erroneously ascribed to an excess in the duration of spring and summer in the northern hemisphere, in consequence of the excentricity of the solar ellipse. The length of the seasons varies with the position of the perihelion (N. 64) of the earth’s orbit for two reasons. On account of the excentricity, small as it is, any line passing through the centre of the sun divides the terrestrial ellipse into two unequal parts, and by the laws of elliptical motion the earth moves through these two portions with unequal velocities. The perihelion always lies in the smaller portion, and there the earth’s motion is the most rapid. In the present position of the perihelion, spring and summer north of the equator exceed by about eight days the duration of the same seasons south of it. And 10,492 years ago the southern hemisphere enjoyed the advantage we now possess from the secular variation of the perihelion. Yet Sir John Herschel has shown that by this alternation neither hemisphere acquires any excess of light or heat above the other; for, although the earth is nearer to the sun while moving through that part of its orbit in which the perihelion lies than in the other part, and consequently receives a greater quantity of light and heat, yet as it moves faster it is exposed to the heat for a shorter time. In the other part of the orbit, on the contrary, the earth, being farther from the sun, receives fewer of his rays; but because its motion is slower, it is exposed to them for a longer time; and, as in both 75cases the quantity of heat and the angular velocity vary exactly in the same proportion, a perfect compensation takes place (N. 144). So that the excentricity of the earth’s orbit has little or no effect on the temperature corresponding to the difference of the seasons.
Sir Charles Lyell, in his excellent works on Geology, refers the increased cold of the northern hemisphere to the operation of existing causes with more probability than most theories that have been advanced in solution of this difficult subject. The loftiest mountains would be represented by a grain of sand on a globe six feet in diameter, and the depth of the ocean by a scratch on its surface. Consequently the gradual elevation of a continent or chain of mountains above the surface of the ocean, or their depression below it, is no very great event compared with the magnitude of the earth, and the energy of its subterranean fires, if the same periods of time be admitted in the progress of geological as in astronomical phenomena, which the successive and various races of extinct beings show to have been immense. Climate is always more intense in the interior of continents than in islands or sea-coasts. An increase of land within the tropics would therefore augment the general heat, and an increase in the temperate and frigid zones would render the cold more severe. Now it appears that most of the European, North Asiatic, and North American continents and islands were raised from the deep after the coal-measures were formed in which the fossil tropical plants are found; and a variety of geological facts indicate the existence of an ancient and extensive archipelago throughout the greater part of the northern hemisphere. Sir Charles Lyell is therefore of opinion that the climate of these islands must have been sufficiently mild, in consequence of the surrounding ocean, to clothe them with tropical plants, and render them a fit abode for the huge animals whose fossil remains are so often found; that the arborescent ferns and the palms of these regions, carried by streams to the bottom of the ocean, were imbedded in the strata which were by degrees heaved up by the subterranean fires during a long succession of ages, till the greater part of the northern hemisphere became dry land as it now is, and that the consequence has been a continual decrease of temperature.
It is evident, from the marine shells found on the tops of the 76highest mountains and in almost every part of the globe, that immense continents have been elevated above the ocean which must have engulfed others. Such a catastrophe would be occasioned by a variation in the position of the axis of rotation on the surface of the earth; for the seas tending to a new equator would leave some portions of the globe and overwhelm others. Now, it is found by the laws of mechanics that in every body, be its form or density what it may, there are at least three axes at right angles to each other, round any one of which, if the solid begins to rotate, it will continue to revolve for ever, provided it be not disturbed by a foreign cause, but that the rotation about any other axis will only be for an instant, and consequently the poles or extremities of the instantaneous axis of rotation would perpetually change their position on the surface of the body. In an ellipsoid of revolution the polar diameter and every diameter in the plane of the equator are the only permanent axes of rotation (N. 145). Hence, if the ellipsoid were to begin to revolve about any diameter between the pole and the equator, the motion would be so unstable that the axis of rotation and the position of the poles would change every instant. Therefore, as the earth does not differ much from this figure, if it did not turn round one of its principal axes, the position of the poles would change daily; the equator, which is 90° distant, would undergo corresponding variations; and the geographical latitudes of all places, being estimated from the equator, assumed to be fixed, would be perpetually changing. A displacement in the position of the poles of only two hundred miles would be sufficient to produce these effects, and would immediately be detected. But, as the latitudes are found to be invariable, it may be concluded that the terrestrial spheroid must have revolved about the same axis for ages. The earth and planets differ so little from ellipsoids of revolution, that in all probability any libration from one axis to another, produced by the primitive impulse which put them in motion, must have ceased soon after their creation from the friction of the fluids at their surface.
Theory also proves that neither nutation, precession, nor any of the disturbing forces that affect the system, have the smallest influence on the axis of rotation, which maintains a permanent position on the surface, if the earth be not disturbed in its rotation by a foreign cause, as the collision of a comet, which might 77have happened in the immensity of time. But, had that been the case, its effects would still have been perceptible in the variations of the geographical latitudes. If we suppose that such an event had taken place, and that the disturbance had been very great, equilibrium could then only have been restored with regard to a new axis of rotation by the rushing of the seas to the new equator, which they must have continued to do till the surface was everywhere perpendicular to the direction of gravity. But it is probable that such an accumulation of the waters would not be sufficient to restore equilibrium if the derangement had been great, for the mean density of the sea is only about a fifth part of the mean density of the earth, and the mean depth of the Pacific Ocean is supposed not to be more than four or five miles, whereas the equatorial diameter of the earth exceeds the polar diameter by about 261⁄2 miles. Consequently the influence of the sea on the direction of gravity is very small. And, as it thus appears that a great change in the position of the axis is incompatible with the law of equilibrium, the geological phenomena in question must be ascribed to an internal cause. Indeed it is now demonstrated that the strata containing marine diluvia, which are in lofty situations, must have been formed at the bottom of the ocean, and afterwards upheaved by the action of subterraneous fires. Besides, it is clear, from the mensuration of the arcs of the meridian and the length of the seconds’ pendulum, as well as from the lunar theory, that the internal strata and also the external outline of the globe are elliptical, their centres being coincident and their axes identical with that of the surface—a state of things which, according to the distinguished author lately quoted, is incompatible with a subsequent accommodation of the surface to a new and different state of rotation from that which determined the original distribution of the component matter. Thus, amidst the mighty revolutions which have swept innumerable races of organized beings from the earth, which have elevated plains and buried mountains in the ocean, the rotation of the earth and the position of the axes on its surface have undergone but slight variations.
The strata of the terrestrial spheroid are not only concentric and elliptical, but the lunar inequalities show that they increase in density from the surface of the earth to its centre. This would certainly have happened if the earth had originally been 78fluid, for the denser parts must have subsided towards the centre as it approached a state of equilibrium. But the enormous pressure of the superincumbent mass is a sufficient cause for the phenomenon. Professor Leslie observes that air compressed into the fiftieth part of its volume has its elasticity fifty times augmented. If it continues to contract at that rate, it would, from its own incumbent weight, acquire the density of water at the depth of thirty-four miles. But water itself would have its density doubled at the depth of ninety-three miles, and would even attain the density of quicksilver at a depth of 362 miles. Descending therefore towards the centre through nearly 4000 miles, the condensation of ordinary substances would surpass the utmost powers of conception. Dr. Young says that steel would be compressed into one-fourth and stone into one-eighth of its bulk at the earth’s centre. However, we are yet ignorant of the laws of compression of solid bodies beyond a certain limit; from the experiments of Mr. Perkins they appear to be capable of a greater degree of compression than has generally been imagined.
But a density so extreme is not borne out by astronomical observation. It might seem to follow therefore that our planet must have a widely cavernous structure, and that we tread on a crust or shell whose thickness bears a very small proportion to the diameter of its sphere. Possibly, too, this great condensation at the central regions may be counterbalanced by the increased elasticity due to a very elevated temperature.
Precession and Nutation—Their Effects on the Apparent Places of the Fixed Stars.
It has been shown that the axis of rotation is invariable on the surface of the earth; and observation as well as theory prove that, were it not for the action of the sun and moon on the matter at the equator, it would remain exactly parallel to itself in every point of its orbit.
The attraction of an external body not only draws a spheroid towards it, but, as the force varies inversely as the square of the distance, it gives it a motion about its centre of gravity, unless when the attracting body is situated in the prolongation of one of the axes of the spheroid. The plane of the equator is inclined to the plane of the ecliptic at an angle of 23° 27ʹ 28ʺ·29; and the inclination of the lunar orbit to the same is 5° 8ʹ 47ʺ·9. Consequently, from the oblate figure of the earth, the sun and moon, acting obliquely and unequally on the different parts of the terrestrial spheroid, urge the plane of the equator from its direction, and force it to move from east to west, so that the equinoctial points have a slow retrograde motion on the plane of the ecliptic of 50ʺ·41 annually. The direct tendency of this action is to make the planes of the equator and ecliptic coincide, but it is balanced by the tendency of the earth to return to stable rotation about the polar diameter, which is one of its principal axes of rotation. Therefore the inclination of the two planes remains constant, as a top spinning preserves the same inclination to the plane of the horizon. Were the earth spherical, this effect would not be produced, and the equinoxes would always correspond with the same points of the ecliptic, at least as far as this kind of motion is concerned. But another and totally different cause which operates on this motion has already been mentioned. The action of the planets on one another and on the sun occasions a very slow variation in the position of the plane of the ecliptic, which affects its inclination to the plane of the equator, and gives 80the equinoctial points a slow but direct motion on the ecliptic of 0ʺ·31 annually, which is entirely independent of the figure of the earth, and would be the same if it were a sphere. Thus the sun and moon by moving the plane of the equator cause the equinoctial points to retrograde on the ecliptic: and the planets by moving the plane of the ecliptic give them a direct motion, though much less than the former. Consequently the difference of the two is the mean precession, which is proved both by theory and observation to be about 50ʺ·1 annually (N. 146).
As the longitudes of all the fixed stars are increased by this quantity, the effects of precession are soon detected. It was accordingly discovered by Hipparchus in the year 128 before Christ, from a comparison of his own observations with those of Timocharis 155 years before. In the time of Hipparchus the entrance of the sun into the constellation Aries was the beginning of spring; but since that time the equinoctial points have receded 30°, so that the constellations called the signs of the zodiac are now at a considerable distance from those divisions of the ecliptic which bear their names. Moving at the rate of 50ʺ·1 annually, the equinoctial points will accomplish a revolution in 25,868 years. But, as the precession varies in different centuries, the extent of this period will be slightly modified. Since the motion of the sun is direct, and that of the equinoctial points retrograde, he takes a shorter time to return to the equator than to arrive at the same stars; so that the tropical year of 365d 5h 48m 49s·7 must be increased by the time he takes to move through an arc of 50ʺ·1, in order to have the length of the sidereal year. The time required is 20m 19s·6, so that the sidereal year contains 365d 6h 9m 9s·6 mean solar days.
The mean annual precession is subject to a secular variation; for, although the change in the plane of the ecliptic in which the orbit of the sun lies be independent of the form of the earth, yet, by bringing the sun, moon, and earth into different relative positions from age to age, it alters the direct action of the two first on the prominent matter at the equator: on this account the motion of the equinox is greater by 0ʺ·455 now than it was in the time of Hipparchus. Consequently the actual length of the tropical year is about 4s·21 shorter than it was at that time. The utmost change that it can experience from this cause amounts to 43 seconds.
81Such is the secular motion of the equinoxes. But it is sometimes increased and sometimes diminished by periodic variations, whose periods depend upon the relative positions of the sun and moon with regard to the earth, and which are occasioned by the direct action of these bodies on the equator. Dr. Bradley discovered that by this action the moon causes the pole of the equator to describe a small ellipse in the heavens, the axes of which are 18ʺ·5 and 13ʺ·674, the longer being directed towards the pole of the ecliptic. The period of this inequality is about 19 years, the time employed by the nodes of the lunar orbit to accomplish a revolution. The sun causes a small variation in the description of this ellipse; it runs through its period in half a year. Since the whole earth obeys these motions, they affect the position of its axis of rotation with regard to the starry heavens, though not with regard to the surface of the earth; for in consequence of precession alone the pole of the equator moves in a circle round the pole of the ecliptic in 25,868 years, and by nutation alone it describes a small ellipse in the heavens every 19 years, on each side of which it deviates every half-year from the action of the sun. The real curve traced in the starry heavens by the imaginary prolongation of the earth’s axis is compounded of these three motions (N. 147). This nutation in the earth’s axis affects both the precession and obliquity with small periodic variations. But in consequence of the secular variation in the position of the terrestrial orbit, which is chiefly owing to the disturbing energy of Jupiter on the earth, the obliquity of the ecliptic is annually diminished, according to M. Bessel, by 0ʺ·457. This variation in the course of ages may amount to 10 or 11 degrees; but the obliquity of the ecliptic to the equator can never vary more than 2° 42ʹ or 3°, since the equator will follow in some measure the motion of the ecliptic.
It is evident that the places of all the celestial bodies are affected by precession and nutation. Their longitudes estimated from the equinox are augmented by precession; but, as it affects all the bodies equally, it makes no change in their relative positions. Both the celestial latitudes and longitudes are altered to a small degree by nutation; hence all observations must be corrected for these inequalities. In consequence of this real motion in the earth’s axis, the pole-star, forming part of the constellation 82of the Little Bear, which was formerly 12° from the celestial pole, is now within 1° 24ʹ of it, and will continue to approach it till it is within 1⁄2°, after which it will retreat from the pole for ages; and 12,934 years hence the star α Lyræ will come within 5° of the celestial pole, and become the polar star of the northern hemisphere.
Mean and Apparent Sidereal Time—Mean and Apparent Solar Time—Equation of Time—English and French Subdivisions of Time—Leap Year—Christian Era—Equinoctial Time—Remarkable Eras depending upon the Position of the Solar Perigee—Inequality of the Lengths of the Seasons in the two Hemispheres—Application of Astronomy to Chronology—English and French Standards of Weights and Measures.
Astronomy has been of immediate and essential use in affording invariable standards for measuring duration, distance, magnitude, and velocity. The mean sidereal day measured by the time elapsed between two consecutive transits of any star at the same meridian (N. 148), and the mean sidereal year which is the time included between two consecutive returns of the sun to the same star, are immutable units with which all great periods of time are compared; the oscillations of the isochronous pendulum measure its smaller portions. By these invariable standards alone we can judge of the slow changes that other elements of the system may have undergone. Apparent sidereal time, which is measured by the transit of the equinoctial point at the meridian of any place, is a variable quantity, from the effects of precession and nutation. Clocks showing apparent sidereal time are employed for observation, and are so regulated that they indicate 0h 0m 0s at the instant the equinoctial point passes the meridian of the observatory. And as time is a measure of angular motion, the clock gives the distances of the heavenly bodies from the equinox by observing the instant at which each passes the meridian, and converting the interval into arcs at the rate of 15° to an hour.
The returns of the sun to the meridian and to the same equinox or solstice have been universally adopted as the measure of our civil days and years. The solar or astronomical day is the time that elapses between two consecutive noons or midnights. It is consequently longer than the sidereal day, on account of the proper motion of the sun during a revolution of the celestial 84sphere. But, as the sun moves with greater rapidity at the winter than at the summer solstice, the astronomical day is more nearly equal to the sidereal day in summer than in winter. The obliquity of the ecliptic also affects its duration; for near the equinoxes the arc of the equator is less than the corresponding arc of the ecliptic, and in the solstices it is greater (N. 149). The astronomical day is therefore diminished in the first case, and increased in the second. If the sun moved uniformly in the equator at the rate of 59ʹ 8ʺ·33 every day, the solar days would be all equal. The time therefore which is reckoned by the arrival of an imaginary sun at the meridian, or of one which is supposed to move uniformly in the equator, is denominated mean solar time, and is given by clocks and watches in common life. When it is reckoned by the arrival of the real sun at the meridian, it is true or apparent time, and is given by dials. The difference between the time shown by a clock and a dial is the equation of time given in the Nautical Almanac, sometimes amounting to as much as sixteen minutes. The apparent and mean time coincide four times in the year; when the sun’s daily motion in right ascension is equal to 59ʹ 8ʺ·33 in a mean solar day, which happens about the 16th of April, the 16th of June, the 1st of September, and the 25th of December.
The astronomical day begins at noon, but in common reckoning the day begins at midnight. In England it is divided into twenty-four hours, which are counted by twelve and twelve; but in France astronomers, adopting the decimal division, divide the day into ten hours, the hour into one hundred minutes, and the minute into a hundred seconds, because of the facility in computation, and in conformity with their decimal system of weights and measures. This subdivision is not now used in common life, nor has it been adopted in any other country; and although some scientific writers in France still employ that division of time, the custom is beginning to wear out. At one period during the French Revolution, the clock in the gardens of the Tuileries was regulated to show decimal time. The mean length of the day, though accurately determined, is not sufficient for the purposes either of astronomy or civil life. The tropical or civil year of 365d 5h 48m 49s·7, which is the time elapsed between the consecutive returns of the sun to the mean equinoxes or solstices, including all the changes of the seasons, is a natural 85cycle peculiarly suited for a measure of duration. It is estimated from the winter solstice, the middle of the long annual night under the north pole. But although the length of the civil year is pointed out by nature as a measure of long periods, the incommensurability that exists between the length of the day and the revolution of the sun renders it difficult to adjust the estimation of both in whole numbers. If the revolution of the sun were accomplished in 365 days, all the years would be of precisely the same number of days, and would begin and end with the sun at the same point of the ecliptic. But as the sun’s revolution includes the fraction of a day, a civil year and a revolution of the sun have not the same duration. Since the fraction is nearly the fourth of a day, in four years it is nearly equal to a revolution of the sun, so that the addition of a supernumerary day every fourth year nearly compensates the difference. But in process of time further correction will be necessary, because the fraction is less than the fourth of a day. In fact, if a bissextile be suppressed at the end of three out of four centuries, the year so determined will only exceed the true year by an extremely small fraction of a day; and if in addition to this a bissextile be suppressed every 4000 years, the length of the year will be nearly equal to that given by observation. Were the fraction neglected, the beginning of the year would precede that of the tropical year, so that it would retrograde through the different seasons in a period of about 1507 years. The Egyptian year began with the heliacal rising of Sirius (N. 150), and contained only 365 days, by which they lost one year in every 1461 years, their Sothaic period, or that cycle in which the heliacal rising of Sirius passes through the whole year and takes place again on the same day. The division of the year into months is very old and almost universal. But the period of seven days, by far the most permanent division of time, and the most ancient monument of astronomical knowledge, was used by the Brahmins in India with the same denominations employed by us, and was alike found in the calendars of the Jews, Egyptians, Arabs, and Assyrians. It has survived the fall of empires, and has existed among all successive generations, a proof of their common origin.
The day of the new moon immediately following the winter solstice in the 707th year of Rome was made the 1st of January of the first year of Julius Cæsar. The 25th of December of his 86forty-fifth year is considered as the date of Christ’s nativity; and the forty-sixth year of the Julian Calendar is assumed to be the first of our era. The preceding year is called the first year before Christ by chronologists, but by astronomers it is called the year 0. The astronomical year begins on the 31st of December at noon; and the date of an observation expresses the days and hours which have actually elapsed since that time.
Since solar and sidereal time are estimated from the passage of the sun and the equinoctial point across the meridian of each place, the hours are different at different places: while it is one o’clock at one place, it is two at another, three at another, &c.; for it is obvious that it is noon at one part of the globe at the same moment that it is midnight at another diametrically opposite to it: consequently an event which happens at one and the same instant of absolute time is recorded at different places as having happened at different times. Therefore, when observations made at different places are to be compared, they must be reduced by computation to what they would have been had they been made under the same meridian. To obviate this it was proposed by Sir John Herschel to employ mean equinoctial time, which is the same for all the world, and independent alike of local circumstances and inequalities in the sun’s motion. It is the time elapsed from the instant the mean sun enters the mean vernal equinox, and is reckoned in mean solar days and parts of a day.
Some remarkable astronomical eras are determined by the position of the major axis of the solar ellipse, which depends upon the direct motion of the perigee (N. 102) and the precession of the equinoxes conjointly, the annual motion of the one being 11ʺ·8, and that of the other 50ʺ·1. Hence the axis, moving at the rate of 61ʺ·9 annually, accomplishes a tropical revolution in 209·84 years. It coincided with the line of the equinoxes 4000 or 4089 years before the Christian era, much about the time chronologists assign for the creation of man. In 6483 the major axis will again coincide with the line of the equinoxes; but then the solar perigee will coincide with the equinox of autumn, whereas at the creation of man it coincided with the vernal equinox. In the year 1246 the major axis was perpendicular to the line of the equinoxes; then the solar perigee coincided with the solstice of summer, and the apogee with the 87solstice of winter. According to La Place, who computed these periods from different data, the last coincidence happened in the year 1250 of our era, which induced him to propose that year as a universal epoch, the vernal equinox of the year 1250 to be the first day of the first year. These eras can only be regarded as approximate, since ancient observations are too inaccurate, and modern observations too recent, to afford data for their precise determination.
The variation in the position of the solar ellipse occasions corresponding changes in the length of the seasons. In its present position spring is shorter than summer, and autumn longer than winter; and while the solar perigee continues as it now is, between the solstice of winter and the equinox of spring, the period including spring and summer will be longer than that including autumn and winter. In this century the difference is between seven and eight days. The intervals will be equal towards the year 6483, when the perigee will coincide with the equinox of spring; but, when it passes that point, the spring and summer taken together will be shorter than the period including the autumn and winter (N. 151). These changes will be accomplished in a tropical revolution of the major axis of the earth’s orbit, which includes an interval of 20,984 years. Were the orbit circular, the seasons would be equal; their difference arises from the excentricity of the orbit, small as it is; but the changes are so trifling as to be imperceptible in the short span of human life.
No circumstance in the whole science of astronomy excites a deeper interest than its application to chronology. “Whole nations,” says La Place, “have been swept from the earth, with their languages, arts, and sciences, leaving but confused masses of ruins to mark the place where mighty cities stood; their history, with the exception of a few doubtful traditions, has perished; but the perfection of their astronomical observations marks their high antiquity, fixes the periods of their existence, and proves that, even at that early time, they must have made considerable progress in science.” The ancient state of the heavens may now be computed with great accuracy; and, by comparing the results of calculation with ancient observations, the exact period at which they were made may be verified if true, or, if false, their error may be detected. If the date be accurate and the observation 88good, it will verify the accuracy of modern tables, and will show to how many centuries they may be extended without the fear of error. A few examples will show the importance of the subject.
At the solstices the sun is at his greatest distance from the equator; consequently his declination at these times is equal to the obliquity of the ecliptic (N. 152), which was formerly determined from the meridian length of the shadow of the stile of a dial on the day of a solstice. The lengths of the meridian shadow at the summer and winter solstices are recorded to have been observed at the city of Layang, in China, 1100 years before the Christian era. From these the distances of the sun from the zenith (N. 153) of the city of Layang are known. Half the sum of these zenith distances determines the latitude, and half their difference gives the obliquity of the ecliptic at the period of the observation; and, as the law of the variation of the obliquity is known, both the time and place of the observations have been verified by computations from modern tables. Thus the Chinese had made some advances in the science of astronomy at that early period. Their whole chronology is founded on the observations of eclipses, which prove the existence of that empire for more than 4700 years. The epoch of the lunar tables of the Indians, supposed by Bailly to be 3000 years before the Christian era, was proved by La Place, from the acceleration of the moon, not to be more ancient than the time of Ptolemy, who lived in the second century after it. The great inequality of Jupiter and Saturn, whose cycle embraces 918 years, is peculiarly fitted for marking the civilization of a people. The Indians had determined the mean motions of these two planets in that part of their periods when the apparent mean motion of Saturn was at the slowest, and that of Jupiter the most rapid. The periods in which that happened were 3102 years before the Christian era, and the year 1491 after it. The returns of comets to their perihelia may possibly mark the present state of astronomy to future ages.
The places of the fixed stars are affected by the precession of the equinoxes; and, as the law of that variation is known, their positions at any time may be computed. Now Eudoxus, a contemporary of Plato, mentions a star situate in the pole of the equator, and it appears from computation that χ Draconis was 89not very far from that place about 3000 years ago; but, as it is only about 2150 years since Eudoxus lived, he must have described an anterior state of the heavens, supposed to be the same that was mentioned by Chiron about the time of the siege of Troy. Thus every circumstance concurs in showing that astronomy was cultivated in the highest ages of antiquity.
It is possible that a knowledge of astronomy may lead to the interpretation of hieroglyphical characters. Astronomical signs are often found on the ancient Egyptian monuments, probably employed by the priests to record dates. The author had occasion to witness an instance of this most interesting application of astronomy, in ascertaining the date of a papyrus, sent from Egypt by Mr. Salt, in the hieroglyphical researches of the late Dr. Thomas Young, whose profound and varied acquirements do honour to his country, and to the age in which he lived. The manuscript was found in a mummy case; it proved to be a horoscope of the age of Ptolemy, and its date was determined from the configuration of the heavens at the time of its construction.
The form of the earth furnishes a standard of weights and measures for the ordinary purposes of life, as well as for the determination of the masses and distances of the heavenly bodies. The length of the pendulum vibrating seconds of mean solar time, in the latitude of London, forms the standard of the British measure of extension. Its approximate length oscillating in vacuo at the temperature of 62° of Fahrenheit, and reduced to the level of the sea (N. 154), was determined by Captain Kater to be 39·1393 inches. The weight of a cubic inch of water at the temperature of 62° of Fahrenheit, barometer 30 inches, was also determined in parts of the imperial troy pound, whence a standard both of weight and capacity was deduced. The French have adopted the mètre, equal to 3·2808992 English feet, for their unit of linear measure, which is the ten-millionth part of the arc of the meridian which extends from the equator to the pole, as deduced from the measures of the separate arc extending from Formentera, the most southern of the Balearic Islands, to Dunkirk. Should the national standards of the two countries ever be lost, both may be recovered, since they are derived from natural and invariable ones. The length of the measure deduced from that of the pendulum would be found again with more 90facility than the mètre. But, as no measure is mathematically exact, an error in the original standard may at length become sensible in measuring a great extent, whereas the error that must necessarily arise in measuring the quadrant of the meridian (N. 155) is rendered totally insensible by subdivision in taking its ten-millionth part. The French have adopted the decimal division, not only in time, but also in their degrees, weights, and measures, on account of the very great facility it affords in computation. It has not been adopted by any other country, though nothing is more desirable than that all nations should concur in using the same standards, not only on account of convenience, but as affording a more definite idea of quantity. It is singular that the decimal division of the day, of space, weights, and measures, was employed in China 4000 years ago; and that at the time Ibn Junis made his observations at Cairo, about the year 1000 of the Christian era, the Arabs were in the habit of employing the vibrations of the pendulum in their astronomical observations as a measure of time.
Tides—Forces that produce them—Origin and Course of Tidal Wave—Its Speed—Three kinds of Oscillations in the Ocean—The Semidiurnal Tides—Equinoctial Tides—Effects of the Declination of the Sun and Moon—Theory insufficient without Observation—Direction of the Tidal Wave—Height of Tides—Mass of Moon obtained from her Action on the Tides—Interference of Undulations—Impossibility of a Universal Inundation—Currents.
One of the most immediate and remarkable effects of a gravitating force external to the earth is the alternate rise and fall of the surface of the sea twice in the course of a lunar day, or 24h 50m 28s of mean solar time. As it depends upon the action of the sun and moon, it is classed among astronomical problems, of which it is by far the most difficult and its explanation the least satisfactory. The form of the surface of the ocean in equilibrio, when revolving with the earth round its axis, is an ellipsoid flattened at the poles; but the action of the sun and moon, especially of the moon, disturbs the equilibrium of the ocean. If the moon attracted the centre of gravity of the earth and all its particles with equal and parallel forces, the whole system of the earth and the waters that cover it would yield to these forces with a common motion, and the equilibrium of the seas would remain undisturbed. The difference of the forces and the inequality of their directions alone disturb the equilibrium.
The particles of water under the moon are more attracted than the centre of gravity of the earth, in the inverse ratio of the square of the distance. Hence they have a tendency to leave the earth, but are retained by their gravitation, which is diminished by this tendency. On the contrary, the moon attracts the centre of the earth more powerfully than she attracts the particles of water in the hemisphere opposite to her; so that the earth has a tendency to leave the waters, but is retained by gravitation, which is again diminished by this tendency. Thus the waters immediately under the moon are drawn from the earth, at the same time that the earth is drawn from those 92which are diametrically opposite to her, in both instances producing an elevation of the ocean of nearly the same height above the surface of equilibrium; for the diminution of the gravitation of the particles in each position is almost the same, on account of the distance of the moon being great in comparison of the radius of the earth. Were the earth entirely covered by the sea, the waters thus attracted by the moon would assume the form of an oblong spheroid whose greater axis would point towards the moon; since the columns of water under the moon, and in the direction diametrically opposite to her, are rendered lighter in consequence of the diminution of their gravitation; and, in order to preserve the equilibrium, the axes 90° distant would be shortened. The elevation, on account of the smaller space to which it is confined, is twice as great as the depression, because the contents of the spheroid always remain the same. If the waters were capable of assuming the form of equilibrium instantaneously, that is, the form of the spheroid, its summit would always point to the moon notwithstanding the earth’s rotation. But, on account of their resistance, the rapid motion produced in them by rotation prevents them from assuming at every instant the form which the equilibrium of the forces acting upon them requires. Hence, on account of the inertia of the waters, if the tides be considered relatively to the whole earth and open seas, there is a meridian about 30° eastward of the moon, where it is always high water both in the hemisphere where the moon is and in that which is opposite. On the west side of this circle the tide is flowing, on the east it is ebbing, and on every part of the meridian at 90° distant it is low water. This great wave, which follows all the motions of the moon as far as the rotation of the earth will permit, is modified by the action of the sun, the effects of whose attraction are in every respect like those produced by the moon, though greatly less in degree. Consequently a similar wave, but much smaller, raised by the sun, tends to follow his motions, which at times combines with the lunar wave, and at others opposes it, according to the relative positions of the two luminaries; but as the lunar wave is only modified a little by the solar, the tides must necessarily happen twice in a day, since the rotation of the earth brings the same point twice under the meridian of the moon in that time, once under the superior and once under the inferior meridian.
93The periodic motions of the waters of the ocean, on the hypothesis of an ellipsoid of revolution, entirely covered by the sea, are, however, very far from according with observation. This arises from the great irregularities in the surface of the earth, which is but partially covered by the sea, from the variety in the depths of the ocean, the manner in which it is spread out on the earth, the position and inclination of the shores, the currents, and the resistance which the waters meet with: causes impossible to estimate generally, but which modify the oscillations of the great mass of the ocean. However, amidst all these irregularities, the ebb and flow of the sea maintain a ratio to the forces producing them sufficient to indicate their nature, and to verify the law of the attraction of the sun and moon on the sea. La Place observes, that the investigation of such relations between cause and effect is no less useful in natural philosophy than the direct solution of problems, either to prove the existence of the causes or to trace the laws of their effects. Like the theory of probabilities, it is a happy supplement to the ignorance and weakness of the human mind.
Since the disturbing action of the sun and moon can only become sensible in a very great extent of deep water, the Antarctic Ocean is the origin and birthplace of our tides. A succession of tidal waves from that source follow one another in a north-westerly direction down the Pacific and Atlantic Oceans, modified as they proceed by the depth of the water and the form of the coasts. For when the sun and moon are in the same meridian, and pass over the mass of waters lying east from Van Diemen’s Land, New Zealand, and the South Pole, the resulting force of their combined attraction, penetrating to the abyss of the deep and boundless circuit of the Southern Ocean, raises a vast wave or ridge of water, which tends to follow the luminaries to the north and west, and continues to flow in that direction long after the bodies cease to act upon it; but it is so retarded by the rotation of the earth and by the inertia of the water, that it does not arrive at the different parts of the coasts till after the moon’s southing (N. 156). When this tidal wave leaves the Antarctic Ocean and enters the Pacific, it rushes along the western coast of America to its farthest end, but it is so much obstructed by the number of islands in the middle of that ocean that it is hardly perceptible among them; while on the east it 94enters the Indian Ocean, strikes with violence on the coasts of Hindostan and the shores at the mouths of the Ganges, and causes the terrific bore in the Hoogly. The part of this tidal wave that enters the Atlantic passes impetuously along the coasts of Africa and America, arriving later and later at each place. It is modified, however, by a tide raised in the Atlantic, which is deep and free from islands; and this combined tidal wave, still coming northward, pours its surge into the Gulf of Fundy to the height of fifty feet; then being deflected by the coast of America at right angles, it rushes eastward, bringing high water to the western coasts of Ireland and England. It then goes round Scotland, brings high water to Aberdeen and the opposite coasts of Norway and Denmark, and, continuing its course to the south, arrives at the mouth of the Thames and fills the channels of that river on the morning of the third day after leaving the Antarctic Ocean.
Thus the tides in our ports are owing to an impulse from the waters of the Antarctic seas raised by the action of the sun and moon. No doubt a similar action raised that tide in the North Polar Ocean which Dr. Kane saw rolling on the northern coast of Greenland in 82° N. latitude, but which, in the present state of the globe, is imprisoned by bars of ice and ice-bound lands.
The tidal wave extends to the bottom of the ocean, and moves uniformly and with great speed in very deep water, variably and slow in shallow water; the time of propagation depends upon the depth of the sea, as well as on the nature and form of the coasts. It varies inversely as the square of the depth—a law which theoretically affords the means of ascertaining the proportionate depth of the sea in different parts. It is one of the great constants of nature, and is to fluids what the pendulum is to solids—a connecting link between time and force.
For example: the tidal wave moves across the Southern Ocean with the velocity of 1000 miles an hour, and in the Atlantic it is scarcely less on account of the deep trough which runs through the centre of that ocean; but the sea is so shallow on the British coast that it takes more time to come from Aberdeen to London than to travel over an arc of 120°, between 60° S. lat. and 60° N. lat.
In deep water the tidal wave is merely a rise and fall of the surface; the water does not advance, though the wave does. Indeed, 95if so heavy a body as water were to move at the rate of 1000 miles an hour, it would cause universal destruction, since in the most violent hurricanes the velocity of the wind is little more than 100 miles an hour. Besides, it is evident that no ship could either sail or steam against it. When the water is shallow, however, there is a motion of translation in the water along with the tide.
In the deep ocean the undulating motion consists of two distinct things—an advancing form and a molecular movement. The motion of each particle of water is in an ellipse lying wholly in the vertical plane; so that, after the momentary displacement during the passage of the wave, they return to their places again. The resistance of the sea-bed is insensible in deep water; but when the tidal wave, which extends to the very bottom of the ocean, comes into shallow water with diminished velocity, the particles of water moving in vertical ellipses strike the bottom, and by reaction the wave rises higher; and that being continually repeated, as the form moves on the wave rises higher and higher, bends more and more forward, till at last it loses its equilibrium, and then both form and water roll to the shore, and the elliptical trajectories of the particles, which in deep water were vertical, incline more and more, till at length they become horizontal. The distance from the shore at which the water begins to be translated depends upon the depth, the nature of the coast, and the form of the shore. Mr. Scott Russell has demonstrated that in shallow water the velocity of the wave is equal to that which a heavy body falling freely by its gravity would acquire in descending through half the depth of the fluid.
It is proved by daily experience, as well as by strict mathematical reasoning, that, if a number of waves or oscillations be excited in a fluid by different forces, each pursues its course and has its effect independently of the rest. Now, in the tides there are three kinds of oscillations, depending on different causes, and producing their effects independently of each other, which may therefore be estimated separately. The oscillations of the first kind, which are very small, are independent of the rotation of the earth, and, as they depend upon the motion of the disturbing body in its orbit, they are of long periods. The second kind of oscillations depend upon the rotation of the earth, therefore their period is nearly a day. The oscillations of the third kind vary 96with an angle equal to twice the angular rotation of the earth, and consequently happen twice in twenty-four hours (N. 157). The first afford no particular interest, and are extremely small; but the difference of two consecutive tides depends upon the second. At the time of the solstices this difference, which ought to be very great according to Newton’s theory, is hardly sensible on our shores. La Place has shown that the discrepancy arises from the depth of the sea, and that if the depth were uniform there would be no difference in the consecutive tides but that which is occasioned by local circumstances. It follows, therefore, that, as this difference is extremely small, the sea, considered in a large extent, must be nearly of uniform depth, that is to say, there is a certain mean depth from which the deviation is not great. The mean depth of the Pacific Ocean is supposed to be about four or five miles, that of the Atlantic only three or four, which, however, is mere conjecture. Possibly the great extent and uniformly small depth of the Atlantic over the telegraphic platform may prevent the difference of the oscillations in question from being perceptible on our shores. From the formulæ which determine the difference of these consecutive tides it is proved that the precession of the equinoxes and the nutation of the earth’s axis are the same as if the sea formed one solid mass with the earth.
The oscillations of the third kind are the semi-diurnal tides so remarkable on our coasts. In these there are two phenomena particularly to be distinguished, one occurring twice in a month, the other twice in a year.
The first phenomenon is, that the tides are much increased in the syzygies (N. 158), or at the time of new and full moon: in both cases the sun and moon are in the same meridian; for when the moon is new they are in conjunction, and when she is full they are in opposition. In each of these positions their action is combined to produce the highest or spring tides under that meridian, and the lowest in those points that are 90° distant. It is observed that the higher the sea rises in full tide, the lower it is in the ebb. The neap tides take place when the moon is in quadrature. They neither rise so high nor sink so low as the spring tides. It is evident that the spring tides must happen twice in a month, since in that time the moon is once new and once full. Theory proves that each partial tide increases as the 97cube of the parallax or apparent diameter of the body producing it, for the greater the apparent diameter the nearer the body and the more intense its action upon the sea; hence the spring tides are much increased when the moon is in perigee, for then she is nearest to the earth.
The second phenomenon in the tides is the augmentation occurring at the time of the equinoxes, when the sun’s declination is zero (N. 159), which happens twice in every year. The spring tides which take place at that time are often much increased by the equinoctial gales, and, on the hypothesis of the whole earth covered by the ocean, would be the greatest possible if the line of the moon’s nodes coincided with that of her perigee, for then the whole action of the luminaries would be in the plane of the equator. But since the Antarctic Ocean is the source of the tides, it is evident that the spring tide must be greatest when the moon is in perigee, and when both luminaries have their highest southern declination, for then they act most directly upon the great circuit of the south polar seas.
The sun and moon are continually making the circuit of the heavens at different distances from the plane of the equator, on account of the obliquity of the ecliptic and the inclination of the lunar orbit. The moon takes about 291⁄2 days to vary through all her declinations, which sometimes extend 283⁄4° on each side of the equator, while the sun requires nearly 3651⁄4 days to accomplish his motions through 231⁄2° on each side of the same plane, so that their combined action causes great variations in the tides. Both the height and time of high water are perpetually changing, and, although the problem does not admit of a general solution, it is necessary to analyse the phenomena which ought to arise from the attraction of the sun and moon, but the result must be corrected in each particular case for local circumstances, so that the theory of the tides in each port becomes really a matter of experiment, and can only be determined by means of a vast number of observations, including many revolutions of the moon’s nodes.
The mean height of the tides will be increased by a very small quantity for ages to come, in consequence of the decrease in the mean distance of the moon from the earth; the contrary effect will take place after that period has elapsed, and the moon’s mean distance begins to increase again, which it will continue to 98do for many ages. Thus the mean distance of the moon and the consequent minute increase in the height of the tides will oscillate between fixed limits for ever.
The height to which the tides rise is much greater in narrow channels than in the open sea, on account of the obstructions they meet with. The sea is so pent up in the British Channel that the tides sometimes rise as much as fifty feet at St. Malo, on the coast of France; whereas on the shores of some of the South Sea islands, near the centre of the Pacific, they do not exceed one or two feet. The winds have great influence on the height of the tides, according as they conspire with or oppose them. But the actual effect of the wind in exciting the waves of the ocean extends very little below the surface. Even in the most violent storms the water is probably calm at the depth of ninety or a hundred fathoms. The tidal wave of the ocean does not reach the Mediterranean nor the Baltic, partly from their position and partly from the narrowness of the Straits of Gibraltar and of the Categat, but it is very perceptible in the Red Sea and in Hudson’s Bay. The ebb and flow of the sea are perceptible in rivers to a very great distance from their estuaries. In the Narrows of Pauxis, in the river of the Amazons, more than five hundred miles from the sea, the tides are evident. It requires so many days for the tide to ascend this mighty stream, that the returning tides meet a succession of those which are coming up; so that every possible variety occurs at some part or other of its shores, both as to magnitude and time. It requires a very wide expanse of water to accumulate the impulse of the sun and moon, so as to render their influence sensible; on that account the tides in the Mediterranean and Black Sea are scarcely perceptible.
These perpetual commotions in the waters are occasioned by forces that bear a very small proportion to terrestrial gravitation: the sun’s action in raising the ocean is only the 1⁄38448000 of gravitation at the earth’s surface, and the action of the moon is little more than twice as much; these forces being in the ratio of 1 to 2.35333, when the sun and moon are at their mean distances from the earth. From this ratio the mass of the moon is found to be only the 1⁄75 part of that of the earth. Had the action of the sun on the ocean been exactly equal to that of the moon, there would have been no neap tides, and the spring tides would have been of twice the height which the action of either the sun or 99moon would have produced separately—a phenomenon depending upon the interference of the waves or undulations.
A stone plunged into a pool of still water occasions a series of waves to advance along the surface, though the water itself is not carried forward, but only rises into heights and sinks into hollows, each portion of the surface being elevated and depressed in its turn. Another stone of the same size, thrown into the water near the first, will occasion a similar set of undulations. Then, if an equal and similar wave from each stone arrive at the same spot at the same time, so that the elevation of the one exactly coincides with the elevation of the other, their united effect will produce a wave twice the size of either. But, if one wave precede the other by exactly half an undulation, the elevation of the one will coincide with the hollow of the other, and the hollow of the one with the elevation of the other; and the waves will so entirely obliterate one another, that the surface of the water will remain smooth and level. Hence, if the length of each wave be represented by 1, they will destroy one another at intervals of 1⁄2, 3⁄2, 5⁄2, &c., and will combine their effects at the intervals 1, 2, 3, &c. It will be found according to this principle, when still water is disturbed by the fall of two equal stones, that there are certain lines on its surface of a hyperbolic form, where the water is smooth in consequence of the waves obliterating each other, and that the elevation of the water in the adjacent parts corresponds to both the waves united (N. 160). Now, in the spring and neap tides arising from the combination of the simple solilunar waves, the spring tide is the joint result of the combination when they coincide in time and place; and the neap tide happens when they succeed each other by half an interval, so as to leave only the effect of their difference sensible. It is, therefore, evident that, if the solar and lunar tides were of the same height, there would be no difference, consequently no neap tides, and the spring tides would be twice as high as either separately. In the port of Batsha, in Tonquin, where the tides arrive by two channels of lengths corresponding to half an interval, there is neither high nor low water on account of the interference of the waves.
The initial state of the ocean has no influence on the tides; for, whatever its primitive conditions may have been, they must soon have vanished by the friction and mobility of the fluid. One of the most remarkable circumstances in the theory of the tides is 100the assurance that, in consequence of the density of the sea being only one-fifth of the mean density of the earth, and the earth itself increasing in density towards the centre, the stability of the equilibrium of the ocean never can be subverted by any physical cause. A general inundation arising from the mere instability of the ocean is therefore impossible. A variety of circumstances, however, tend to produce partial variations in the equilibrium of the seas, which is restored by means of currents. Winds and the periodical melting of the ice at the poles occasion temporary watercourses; but by far the most important causes are the centrifugal force induced by the velocity of the earth’s rotation, and variations in the density of the sea.
The centrifugal force may be resolved into two forces—one perpendicular, and another tangent to the earth’s surface (N. 161). The tangential force, though small, is sufficient to make the fluid particles within the polar circles tend towards the equator, and the tendency is much increased by the immense evaporation in the equatorial regions from the heat of the sun, which disturbs the equilibrium of the ocean. To this may also be added the superior density of the waters near the poles, from their low temperature. In consequence of the combination of all these circumstances, two great currents perpetually set from each pole towards the equator. But, as they come from latitudes where the rotatory motion of the surface of the earth is very much less than it is between the tropics, on account of their inertia, they do not immediately acquire the velocity with which the solid part of the earth’s surface is revolving at the equatorial regions; from whence it follows that, within twenty-five or thirty degrees on each side of the line, the ocean has a general motion from east to west, which is much increased by the action of the trade winds. Both in the Pacific and Atlantic currents of enormous magnitude are deflected by the continents and islands to the north and south from this mighty mass of rushing waters, which convey the warmth of the equator to temper the severity of the polar regions, while to maintain the equilibrium of the seas counter currents of cold water are poured from the polar oceans to mingle with the warm waters at the line, so that a perpetual circulation is maintained.
Icebergs are sometimes drifted as far as the Azores from the Polar seas, and from the south pole they have come even to the 101Cape of Good Hope. But the ice which encircles the south pole extends to lower latitudes by 10° than that which surrounds the north. In consequence of the polar current Sir Edward Parry was obliged to give up his attempt to reach the north pole in the year 1827, because the fields of ice were drifting to the south faster than his party could travel over them to the north.
Kotzebue and Sir James Ross found a stratum of constant temperature in the ocean at a depth depending upon the latitude: at the equator it is at the depth of 7200 feet, from whence it gradually rises till it comes to the surface in both hemispheres about the latitude of 56° 26ʹ, where the water has the same temperature at all depths; it then descends to 4500 feet below the surface about the 70th parallel both in the Arctic and Antarctic Seas. The temperature of that aqueous zone is about 39°·5 of Fahrenheit.[7] It divides the surface of the ocean into five great zones of temperature, namely, a medial region, in which the highest mean temperature is 82° Fahr., two temperate zones each of 39°·5 Fahr., and two polar basins at the freezing point of salt water.
Molecular Forces—Permanency of the ultimate Particles of Matter—Interstices—Mossotti’s Theory—Rankin’s Theory of Molecular Vortices—Gases reduced to Liquids by Pressure—Gravitation of Particles—Cohesion—Crystallization—Cleavage—Isomorphism—Minuteness of the Particles—Height of Atmosphere—Chemical Affinity—Definite Proportions and Relative Weights of Atoms—Faraday’s Discovery with regard to Affinity—Capillary Attraction.
The oscillations of the atmosphere, and its action upon the rays of light coming from the heavenly bodies, connect the science of astronomy with the equilibrium and movements of fluids and the laws of molecular attraction. Hitherto that force has been under consideration which acts upon masses of matter at sensible distances; but now the effects of such forces are to be considered as act at inappreciable distances upon the ultimate molecules of material bodies.
All substances consist of an assemblage of material particles, or molecules, which are far too small to be visible by any means human ingenuity has yet been able to devise, and which are much beyond the limits of our perceptions. They neither can be created nor destroyed; bodies may be burned, but their particles are not consumed—they are merely liberated from one combination to enter into another, nor are their peculiar properties ever changed; whatever combinations they may enter into, they are ever and invariably the same.
Since every known substance may be reduced in bulk by pressure, it follows that the particles of matter are not in actual contact, but are separated by interstices; and it is evident that the smaller the interstitial spaces the greater the density. These spaces appear to be filled with air in some cases, as may be inferred from certain semi-opaque minerals and other substances becoming transparent when plunged into water. Sometimes they may possibly contain some unknown and highly elastic fluid, such as Sir David Brewster has discovered in the minute cavities of various minerals, which occasionally causes them to explode 103under the hands of the lapidary; but as it is inconceivable that the particles of matter should act upon one another without some means of communication, it is presumed that the interstices of material substances contain a portion of the ethereal medium with which the regions of space are filled.
The various hypotheses that have been formed as to the nature and action of the forces which unite the particles of matter, have been successively given up as science advanced, and now nothing decisive has been attained, although Professor Mossotti, of Pisa, by a very able analysis, has endeavoured to prove the identity of the cohesive force with gravitation. As the particles of material bodies are not in actual contact, he supposes that each is surrounded by an atmosphere of the ethereal medium, which he conceives to be electricity; moreover he assumes that the atoms of the medium repel one another, that the particles of matter also repel one another, but with less intensity, and that there is a mutual attraction between the particles of matter and the atoms of the medium, forces which are assumed to vary inversely as the square of the distance.
Hence, when the material molecules of a body are inappreciably near to one another, they mutually repel each other with a force which diminishes rapidly as the infinitely small distance between the material molecules augments, and at last vanishes. When the molecules are still farther apart, the force becomes attractive. At that particular point where the change takes place the forces of repulsion and attraction balance each other, so that the molecules of a body are neither disposed to approach nor recede, but remain in equilibrio. If we try to press them nearer, the repulsive force resists the attempt; and if we endeavour to break the body so as to tear the particles asunder, the attractive force predominates and keeps them together. This is what constitutes the cohesive force, or force of aggregation, by which the molecules of all substances are united. The limits of the distance at which the negative action becomes positive vary according to the temperature and nature of the molecules, and determine whether the body which they form be solid, liquid, or aëriform.
Beyond this neutral point the attractive force increases as the distance between the molecules augments till it attains a maximum; when the particles are more apart, it diminishes; and, as soon as they are separated by finite or sensible distances, it varies 104directly as their mass and inversely as the square of the distance, which is precisely the law of universal gravitation.
Thus, on the hypothesis that the mutual repulsion between the electric atoms is a little more powerful than the mutual repulsion between the particles of matter, the ether and the matter attract each other with unequal intensities, which leaves an excess of attractive force constituting gravitation. As the gravitating force is in operation wherever there is matter, the ethereal electric medium must encompass all the bodies in the universe; and, as it is utterly incomprehensible that the celestial bodies should exert a reciprocal attraction through a void, the Professor concludes that the ethereal electrical medium fills all space.
It is true that this connexion between the molecular forces and gravitation depends upon hypothesis; but in the greater number of physical investigations some hypothesis is requisite in the first instance to aid the imperfection of our senses; and when the phenomena of nature accord with the assumption, we are justified in believing it to be a general law.
Mr. Rankin’s theory of molecular vortices, or the molecular structure of matter, is independent of electricity. According to his hypothesis, each atom of matter consists of an inappreciably small nucleus, encompassed by an elastic ethereal atmosphere which is retained in its position by attractive forces directed towards the molecule, whilst the molecules attract each other in the direction of straight lines joining their centres. The nuclei may either be solid, or a high condensation of the atmospheres which surround each with decreasing density. When the attraction between the molecules is such that the elasticity of the atmospheres is insensible, the body is a perfect solid, the rigidity of which bears a certain definite proportion to the elasticity of the volume. When the atmospheres are less condensed and the attraction of the molecules merely produces a cohesive force sufficient to balance the atomic elasticity of the atmosphere, the body is a perfect liquid; and when the attraction of the molecules is very small compared with the elasticity of their ethereal atmospheres, the body is a perfect gas. These atmospheres are supposed to be portions of the ethereal medium which penetrates into the interstices of every substance, and their elasticity to be due to the heat generated by the centrifugal force or oscillations among their atoms, for motion is the cause of heat, the force 105producing the motions varying simply as the density of the ether.
In aëriform fluids, although the particles are more remote from each other than in liquids and solids, yet the pressure may be so great as to reduce an aëriform fluid to a liquid, and a liquid to a solid. Dr. Faraday has reduced some of the gases to a liquid state by very great compression; but although atmospheric air is capable of a diminution of volume to which we do not know a limit, it has hitherto always retained its gaseous qualities, and resumes its primitive volume the instant the pressure is removed. Substances are said to be more or less elastic, according to the facility with which they regain their bulk or volume when the pressure is removed; thus liquids resist compression on account of their elasticity, and in solids the resistance is much greater but variable, and the effort required to break a substance is a measure of the cohesive force exerted by its particles. In stone, iron, steel, and all brittle and hard substances, the cohesion of the particles is powerful but of small extent; in elastic bodies, on the contrary, its action is weak, but more extensive. An infinite variety of conditions may be observed in the fusion of metals and other substances passing from hardness to toughness, viscidity, and through all the other stages to perfect fluidity and even to vapour. Since all bodies expand by heat, the cohesive force is weakened by increase of temperature. The cohesion of matter or the strength of substances forms an important branch of study in engineering.
Every particle of matter, whether it forms a constituent part of a solid, liquid, or aëriform fluid, is subject to the law of gravitation. The weight of the atmosphere, of gases and vapour, shows that they consist of gravitating particles. In liquids the cohesive force is not sufficiently powerful to resist the action of gravitation. Therefore, although their component particles still maintain their connexion, the liquid is scattered by their weight, unless when it is confined in a vessel or has already descended to the lowest point possible, and assumed a level surface from the mobility of its particles and the influence of the gravitating forces, as in the ocean, or a lake. Solids would also fall to pieces by the weight of their particles, if the force of cohesion were not powerful enough to resist the efforts of gravitation.
The phenomena arising from the force of cohesion are innumerable. 106The spherical form of rain-drops; the difficulty of detaching a plate of glass from the surface of water; the force with which two plane surfaces adhere when pressed together; the drops that cling to the window-glass in a shower of rain—are all effects of cohesion entirely independent of atmospheric pressure, and are included in the same analytical formula (N. 162) which expresses all the circumstances accurately, although the laws according to which the forces of cohesion and repulsion vary are unknown. It is more than probable that the spherical form of the sun and planets is due to the force of cohesion, as they have every appearance of having been at one period in a state of fusion.
A very remarkable instance has occasionally been observed in plate-glass manufactories. After the large plates of glass of which mirrors are to be made have received their last polish, they are carefully wiped and laid on their edges with their surfaces resting on one another. In the course of time the cohesion has sometimes been so powerful, that they could not be separated without breaking. Instances have occurred where two or three have been so perfectly united, that they have been cut and their edges polished as if they had been fused together; and so great was the force required to make the surfaces slide that one tore off a portion of the surface of the other.
In liquids and gases the forms of the particles have no influence, they are so far apart; but the structure of solids varies according to the sides which the particles present to one another during their aggregation. Nothing is known of their form further than the dissimilarity of their different sides in certain cases, which appears from their reciprocal attractions during crystallisation being more or less powerful according to the sides they present to one another. Crystallisation is an effect of molecular attraction regulated by certain laws, according to which atoms of the same kind of matter unite in regular forms—a fact easily proved by dissolving a piece of alum in pure water. The mutual attraction of the particles is destroyed by the water; but, if it be evaporated, they unite, and form in uniting eight-sided figures called octahedrons (N. 163). These however are not all the same. Some have their angles cut off, others their edges, and some both, while the remainder take the regular form. It is quite clear that the same circumstances which cause the 107aggregation of a few particles would, if continued, cause the addition of more; and the process would go on as long as any particles remain free round the primitive nucleus, which would increase in size, but would remain unchanged in form, the figure of the particles being such as to maintain the regularity and smoothness of the surfaces of the solid and their mutual inclinations. A broken crystal will by degrees resume its regular figure when put back again into the solution of alum, which shows that the internal and external particles are similar, and have a similar attraction for the particles held in solution. The original conditions of aggregation which make the molecules of the same substance unite in different forms must be very numerous, since of carbonate of lime alone there are many hundred varieties; and certain it is, from the motion of polarised light through rock crystal, that a very different arrangement of particles is requisite to produce an extremely small change in external form. A variety of substances in crystallising combine chemically with a certain portion of water which in a dry state forms an essential part of their crystals, and, according to the experiments of MM. Haidinger and Mitscherlich, seems in some cases to give the peculiar determination to their constituent molecules. These gentlemen have observed that the same substance crystallising at different temperatures unites with different quantities of water and assumes a corresponding variety of forms. Seleniate of zinc, for example, unites with three different portions of water, and assumes three different forms, according as its temperature in the act of crystallising is hot, lukewarm, or cold. Sulphate of soda also, which crystallises at 90° of Fahrenheit without water of crystallisation, combines with water at the ordinary temperature, and takes a different form. Heat appears to have a great influence on the phenomena of crystallisation, not only when the particles of matter are free, but even when firmly united, for it dissolves their union, and gives them another determination. Professor Mitscherlich found that prismatic crystals of sulphate of nickel (N. 164), exposed to a summer’s sun in a close vessel, had their internal structure so completely altered without any exterior change, that when broken open they were composed internally of octahedrons with square bases. The original aggregation of the internal particles had been dissolved, and a disposition given to arrange themselves in a crystalline 108form. Crystals of sulphate of magnesia and of sulphate of zinc, gradually heated in alcohol till it boils, lose their transparency by degrees, and when opened are found to consist of innumerable minute crystals totally different in form from the whole crystals; and prismatic crystals of zinc (N. 165) are changed in a few seconds into octahedrons by the heat of the sun: other instances might be given of the influence of even moderate degrees of temperature on molecular attraction in the interior of substances. It must be observed that these experiments give entirely new views with regard to the constitution of solid bodies. We are led from the mobility of fluids to expect great changes in the relative positions of their molecules, which must be in perpetual motion even in the stillest water or calmest air; but we were not prepared to find motion to such an extent in the interior of solids. That their particles are brought nearer by cold and pressure, or removed farther from one another by heat, might be expected; but it could not have been anticipated that their relative positions could be so entirely changed as to alter their mode of aggregation. It follows, from the low temperature at which these changes are effected, that there is probably no portion of inorganic matter that is not in a state of relative motion.
Professor Mitscherlich’s discoveries with regard to the forms of crystallised substances, as connected with their chemical character, have thrown additional light on the constitution of material bodies. There is a certain set of crystalline forms which are not susceptible of variation, as the die or cube (N. 166), which may be small or large, but is invariably a solid bounded by six square surfaces or planes. Such also is the tetrahedron (N. 167) or four-sided solid contained by four equal-sided triangles. Several other solids belong to this class, which is called the Tessular system of crystallisation. There are other crystals which, though bounded by the same number of sides, and having the same form, are yet susceptible of variation; for instance, the eight-sided figure with a square base, called an octahedron (N. 168), which is sometimes flat and low, and sometimes acute and high. It was formerly believed that identity of form in all crystals not belonging to the Tessular system indicated identity of chemical composition. Professor Mitscherlich, however, has shown that substances differing to a certain degree in chemical composition have the property of assuming the same 109crystalline form. For example, the neutral phosphate of soda and the arseniate of soda crystallise in the very same form, contain the same quantities of acid, alkali, and water of crystallisation; yet they differ so far, that one contains arsenic and the other an equivalent quantity of phosphorus. Substances having such properties are said to be isomorphous, that is, equal in form. Of these there are many groups, each group having the same form, and similarity though not identity of chemical composition. For instance, one of the isomorphous groups is that consisting of certain chemical substances called the protoxides of iron, copper, zinc, nickel, and manganese, all of which are identical in form and contain the same quantity of oxygen, but differ in the respective metals they contain, which are, however, nearly in the same proportion in each. All these circumstances tend to prove that substances having the same crystalline form must consist of ultimate atoms having the same figure and arranged in the very same order; so that the form of crystals is dependent on their atomic constitution.
All crystallised bodies have joints called cleavages, at which they split more easily than in other directions; on this property the whole art of cutting diamonds depends. Each substance splits in a manner and in forms peculiar to itself. For example, all the hundreds of forms of carbonate of lime split into six-sided figures, called rhombohedrons (N. 169), whose alternate angles measure 105·55° and 75·05°, however far the division may be carried; therefore the ultimate particle of carbonate of lime is presumed to have that form. However this may be, it is certain that all the various crystals of that mineral may be formed by building up six-sided solids of the form described, in the same manner as children build houses with miniature bricks. It may be imagined that a wide difference may exist between the particles of an unformed mass and a crystal of the same substance—between the common shapeless limestone and the pure and limpid crystal of Iceland spar; yet chemical analysis detects none; their ultimate atoms are identical, and crystallisation shows that the difference arises only from the mode of aggregation. Besides, all substances either crystallise naturally, or may be made to do so by art. Liquids crystallise in freezing, vapours by sublimation (N. 170); and hard bodies, when fused, crystallise in cooling. Hence it may be inferred that all substances are 110composed of atoms, on whose magnitude, density, and form, their nature and qualities depend; and, as these qualities are unchangeable, the ultimate particles of matter must be incapable of wear—the same now as when created.
The size of the ultimate particles of matter must be small in the extreme. Organised beings, possessing life and all its functions, have been discovered so small, that a million of them would occupy less space than a grain of sand. The malleability of gold, the perfume of musk, the odour of flowers, and many other instances might be given of the excessive minuteness of the atoms of matter. Supposing the density of the air at the surface of the earth to be represented by unity, Sir John Herschel has shown that, under any hypothesis as to its atoms, it would require a fraction having at least 1370 figures in its denominator to express its tenuity in the interplanetary space; yet the definite proportions of chemical compounds afford a proof that divisibility of matter has a limit. The cohesive force, which has been the subject of the preceding considerations, only unites particles of the same kind of matter; whereas affinity, which is the cause of chemical compounds, is the mutual attraction between particles of different kinds of matter, generally producing a compound which has no sensible property in common with its component parts except that of their combined gravity, as, for example, water, which is a compound of oxygen and hydrogen gases. It is merely a result of the electrical state of the particles, chemical affinity and electricity being only forms of the same power. In most cases it produces electricity, as in the oxidation of metals and combustion, and in every case without exception heat is evolved by bodies while combining chemically; and as heat is an expansive force, chemical action is changed into mechanical expansion, but it is not known in this case why heat is produced, nor the manner in which the particles act.
It is a permanent and universal law in vast numbers of unorganised bodies that their composition is definite and invariable, the same compound always consisting of the same elements united together in the same proportions. Two substances may indeed be mixed; but they will not combine to form a third substance different from both, unless their component particles unite in definite proportions; that is to say, one part by weight of one of the substances will unite with one part by weight of the 111other, or with two parts, or three, or four, &c., so as to form a new substance; but in any other proportions they will only be mechanically mixed. For example, one part by weight of hydrogen gas will combine with eight parts by weight of oxygen gas, and form water; or it will unite with sixteen parts by weight of oxygen, and form a substance called deutoxide of hydrogen; but, added to any other weight of oxygen, it will produce one or both of these compounds mingled with the portion of oxygen or hydrogen in excess. The law of definite proportion established by Dr. Dalton, on the principle that every compound body consists of a combination of the atoms of its constituent parts, is of universal application, and is in fact one of the most important discoveries in physical science, furnishing information previously unhoped for with regard to the most secret and minute operations of nature, in disclosing the relative weights of the ultimate atoms of matter. Thus an atom of oxygen uniting with an atom of hydrogen forms the compound water; but, as every drop of water however small consists of eight parts by weight of oxygen and one part by weight of hydrogen, it follows that an atom of oxygen is eight times heavier than an atom of hydrogen. In the same manner sulphuretted hydrogen gas consists of sixteen parts by weight of sulphur and one of hydrogen; therefore an atom of sulphur is sixteen times heavier than an atom of hydrogen. Also carbonic oxide is constituted of six parts by weight of carbon and eight of oxygen; and, as an atom of oxygen has eight times the weight of an atom of hydrogen, it follows that an atom of carbon is six times heavier than one of hydrogen. Since the same definite proportion holds in the composition of a vast number of substances that have been examined, it has been concluded that there are great differences in the weights of the ultimate particles of matter. Although Dalton’s law is fully established, yet instances have occurred from which it appears that the atomic theory deduced from it is not always maintained. M. Gay Lussac discovered that gases unite together by their bulk or volumes, in such simple and definite proportions as one to one, one to two, one to three, &c. For example, one volume or measure of oxygen unites with two volumes or measures of hydrogen in the formation of water.
Dr. Faraday has proved, by experiments on bodies both in solution and fusion, that chemical affinity is merely a result of 112the electrical state of the particles of matter. Now it must be observed that the composition of bodies, as well as their decomposition, may be accomplished by means of electricity; and Dr. Faraday has found that this chemical composition and decomposition, by a given current of electricity, is always accomplished according to the laws of definite proportions; and that the quantity of electricity requisite for the decomposition of a substance is exactly the quantity necessary for its composition. Thus the quantity of electricity which can decompose a grain weight of water is exactly equal to the quantity of electricity which unites the elements of that grain of water together, and is equivalent to the quantity of atmospheric electricity which is active in a very powerful flash of lightning. This law is universal, and of that high and general order which characterises all great discoveries. Chemical force is extremely powerful. A pound of the best coal gives when burnt sufficient heat to raise the temperature of 8086 pounds of water one Centigrade degree, whence Professor Helmholtz of Bonn has computed that the magnitude of the chemical force of attraction between the particles of a pound of coal and the quantity of oxygen that corresponds to it, is capable of lifting a weight of 100 pounds to the height of 20 miles.
Dr. Faraday has given a singular instance of cohesive force inducing chemical combination, by the following experiment, which seems to be nearly allied to the discovery made by M. Dœbereiner, in 1823, of the spontaneous combustion of spongy platinum (N. 171) exposed to a stream of hydrogen gas mixed with common air. A plate of platinum with extremely clean surfaces, when plunged into oxygen and hydrogen gas mixed in the proportions which are found in the constitution of water, causes the gases to combine and water to be formed, the platinum to become red-hot, and at last an explosion to take place; the only conditions necessary for this curious experiment being excessive purity in the gases and in the surface of the plate. A sufficiently pure metallic surface can only be obtained by immersing the platinum in very strong hot sulphuric acid and then washing it in distilled water, or by making it the positive pole of a galvanic pile in dilute sulphuric acid. It appears that the force of cohesion, as well as the force of affinity, exerted by particles of matter, extends to all the particles within a very minute distance. Hence the 113platinum, while drawing the particles of the two gases towards its surface by its great cohesive attraction, brings them so near to one another that they come within the sphere of their mutual affinity, and a chemical combination takes place. Dr. Faraday attributes the effect in part also to a diminution in the elasticity of the gaseous particles on their sides adjacent to the platinum, and to their perfect mixture or association, as well as to the positive action of the metal in condensing them against its surface by its attractive force. The particles when chemically united run off the surface of the metal in the form of water by their gravitation, or pass away as aqueous vapour and make way for others.
The oscillations of the atmosphere, and the changes in its temperature, are measured by variations in the heights of the barometer and thermometer. But the actual length of the liquid columns depends not only upon the force of gravitation, but upon the cohesive force or reciprocal attraction between the molecules of the liquid and those of the tube containing it. This peculiar action of the cohesive force is called capillary attraction or capillarity. If a glass tube of extremely fine bore, such as a small thermometer tube, be plunged into a cup of water or spirit of wine, the liquid will immediately rise in the tube above the level of that in the cup; and the surface of the little column thus suspended will be a hollow hemisphere, whose diameter is the interior diameter of the tube. If the same tube be plunged into a cupful of mercury, the liquid will also rise in the tube, but it will never attain the level of that in the cup, and its surface will be a hemisphere whose diameter is also the diameter of the tube (N. 172). The elevation or depression of the same liquid in different tubes of the same matter is in the inverse ratio of their internal diameters (N. 173), and altogether independent of their thickness; whence it follows that the molecular action is insensible at sensible distances, and that it is only the thinnest possible film of the interior surface of the tubes that exerts a sensible action on the liquid. So much indeed is this the case, that, when tubes of the same bore are completely wetted with water throughout their whole extent, mercury will rise to the same height in all of them, whatever be their thickness or density, because the minute coating of moisture is sufficient to remove the internal column of mercury beyond the sphere of attraction 114of the tube, and to supply the place of a tube by its own capillary attraction. The forces which produce the capillary phenomena are the reciprocal attraction of the tube and the liquid, and of the liquid particles on one another; and, in order that the capillary column may be in equilibrio, the weight of that part of it which rises above or sinks below the level of the liquid in the cup must balance these forces.
The estimation of the action of the liquid is a difficult part of this problem. La Place, Dr. Young, and other mathematicians, have considered the liquid within the tube to be of uniform density; but M. Poisson, in one of those masterly productions in which he elucidates the most abstruse subjects, has proved that the phenomena of capillary attraction depend upon a rapid decrease in the density of the liquid column throughout an extremely small space at its surface. Every indefinitely thin layer of a liquid is compressed by the liquid above it, and supported by that below. Its degree of condensation depends upon the magnitude of the compressive force; and, as this force decreases rapidly towards the surface, where it vanishes the density of the liquid decreases also. M. Poisson has shown that, when this force is omitted, the capillary surface becomes plane, and that the liquid in the tube will neither rise above nor sink below the level of that in the cup. In estimating the forces, it is also necessary to include the variation in the density of the capillary surface round the edges from the attraction of the tube.
The direction of the resulting force determines the curvature of the surface of the capillary column. In order that a liquid may be in equilibrio, the force resulting from all the forces acting upon it must be perpendicular to the surface. Now it appears that, as glass is more dense than water or alcohol, the resulting force will be inclined towards the interior side of the tube; therefore the surface of the liquid must be more elevated at the sides of the tube than in the centre in order to be perpendicular to it, so that it will be concave as in the thermometer. But, as glass is less dense than mercury, the resulting force will be inclined from the interior side of the tube (N. 174), so that the surface of the capillary column must be more depressed at the sides of the tube than in the centre, in order to be perpendicular to the resulting force, and is consequently convex, as may be perceived 115in the mercury of the barometer when rising. The absorption of moisture by sponges, sugar, salt, &c., are familiar examples of capillary attraction. Indeed the pores of sugar are so minute, that there seems to be no limit to the ascent of the liquid. Wine is drawn up in a curve on the interior surface of a glass; tea rises above its level on the side of a cup; but, if the glass or cup be too full, the edges attract the liquid downwards, and give it a rounded form. A column of liquid will rise above or sink below its level between two plane parallel surfaces when near to one another, according to the relative densities of the plates and the liquid (N. 175); and the phenomena will be exactly the same as in a cylindrical tube whose diameter is double the distance of the plates from each other. If the two surfaces be very near to one another, and touch each other at one of their upright edges, the liquid will rise highest at the edges that are in contact, and will gradually diminish in height as the surfaces become more separated. The whole outline of the liquid column will have the form of a hyperbola. Indeed, so universal is the action of capillarity, that solids and liquids cannot touch one another without producing a change in the form of the surface of the liquid.
The attractions and repulsions arising from capillarity present many curious phenomena. If two plates of glass or metal, both of which are either dry or wet, be partly immersed in a liquid parallel to one another, the liquid will be raised or depressed close to their surfaces, but will maintain its level through the rest of the space that separates them. At such a distance they neither attract nor repel one another; but the instant they are brought so near as to make the level part of the liquid disappear, and the two curved parts of it meet, the two plates will rush towards each other and remain pressed together (N. 176). If one of the surfaces be wet and the other dry, they will repel one another when so near as to have a curved surface of liquid between them; but, if forced to approach a little nearer, the repulsion will be overcome, and they will attract each other as if they were both wet or both dry. Two balls of pith or wood floating in water, or two balls of tin floating in mercury, attract one another as soon as they are so near that the surface of the liquid is curved between them. Two ships in the ocean may be 116brought into collision by this principle. But two balls, one of which is wet and the other dry, repel one another as soon as the liquid which separates them is curved at its surface. A bit of tea-leaf is attracted by the edge of the cup if wet, and repelled when dry, provided it be not too far from the edge and the cup moderately full; if too full, the contrary takes place. It is probable that the rise of the sap in vegetables is in some degree owing to capillarity.
Analysis of the Atmosphere—Its Pressure—Law of Decrease in Density—Law of Decrease in Temperature—Measurement of Heights by the Barometer—Extent of the Atmosphere—Barometrical Variations—Oscillations—Trade-Winds—Cloud-Ring—Monsoons—Rotation of Winds—Laws of Hurricanes.
The atmosphere is not homogeneous. It appears from analysis that, of 100 parts, 99·5 consist of nitrogen and oxygen gases mixed in the proportions of 79 to 21 of volume, the remainder consists of 0·05 parts of carbonic acid and on an average 0·45 of aqueous vapour. These proportions are found to be the same at all heights hitherto attained by man. The air is an elastic fluid, resisting pressure in every direction, and is subject to the law of gravitation. As the space in the top of the tube of a barometer is a vacuum, the column of mercury suspended by the pressure of the atmosphere on the surface of that in the cistern is a measure of its weight. Consequently every variation in the density occasions a corresponding rise or fall in the barometrical column. At the level of the sea in latitude 42°, and at the temperature of melting ice, the mean height of the barometer is 29·922 or 30 inches nearly. The pressure of the atmosphere is about fifteen pounds on every square inch; so that the surface of the whole globe sustains a weight of 11,671,000,000 hundreds of millions of pounds. Shell-fish, which have the power of producing a vacuum, adhere to the rocks by a pressure of fifteen pounds upon every square inch of contact.
The atmosphere when in equilibrio is an ellipsoid flattened at the poles from its rotation with the earth. In that state its strata are of uniform density at equal heights above the level of the sea; but since the air is both heavy and elastic, its density necessarily diminishes in ascending above the surface of the earth; for each stratum of air is compressed only by the weight above it. Therefore the upper strata are less dense because they are less compressed than those below them. Whence it is easy to show, supposing the temperature to be constant, that if the 118heights above the earth be taken in increasing arithmetical progression, that is, if they increase by equal quantities, as by a foot or a mile, the densities of the strata of air, or the heights of the barometer which are proportionate to them, will decrease in geometrical progression. For example, at the level of the sea if the mean height of the barometer be 29·922 inches, at the height of 18,000 feet it will be 14·961 inches, or one half as great; at the height of 36,000 feet it will be one-fourth as great; at 54,000 feet it will be one-eighth, and so on. Sir John Herschel has shown that the actual decrease is much more rapid, and that, in any hypothesis that has been formed with regard to the divisibility of the aërial atoms, a vacuum exists at the height of 80 or 90 miles above the earth’s surface, inconceivably more perfect than any that can be produced in the best air-pumps. Indeed the decrease in density is so rapid that three-fourths of all the air contained in the atmosphere is within four miles of the earth; and, as its superficial extent is 200 millions of square miles, its relative thickness is less than that of a sheet of paper when compared with its breadth. The air even on mountain tops is sufficiently rare to diminish the intensity of sound, to affect respiration, and to occasion a loss of muscular strength. The blood burst from the lips and ears of M. de Humboldt as he ascended the Andes; and he experienced the same difficulty in kindling and maintaining a fire at great heights which Marco Polo, the Venetian, felt on the mountains of Central Asia. M. Gay-Lussac ascended in a balloon to the height of 4·36 miles, and he suffered greatly from the rarity of the air. It is true that at the height of thirty-seven miles the atmosphere is still dense enough to reflect the rays of the sun when 18° below the horizon; but the tails of comets show that extremely attenuated matter is capable of reflecting light. And although, at the height of fifty miles, the bursting of the meteor of 1783 was heard on earth like the report of a cannon, it only proves the immensity of the explosion of a mass half a mile in diameter, which could produce a sound capable of penetrating air three thousand times more rare than that we breathe. But even these heights are extremely small when compared with the radius of the earth.
The density of the air is modified by various circumstances, chiefly by changes of temperature, because heat dilates the air and cold contracts it, varying 1⁄480 of the whole bulk when at 32° 119for every degree of Fahrenheit’s thermometer. Experience shows that the heat of the air decreases as the height above the surface of the earth increases. It appears that the mean temperature of space is 226° below the zero point of Fahrenheit by the theories of Fourier and Pouillet, but Sir John Herschel has computed it to be -239° Fahr. from observations made during the ascent in balloons. Such would probably be the temperature of the surface of the earth also, were it not for the non-conducting power of the air, whence it is enabled to retain the heat of the sun’s rays, which the earth imbibes and radiates in all directions. The decrease in heat is very irregular; each authority gives a different estimate, because it varies with latitude and local circumstances, but from the mean of five different statements it seems to be about one degree for every 334 feet; the mean of observations made in balloons is 400 feet, which is probably nearer the truth. This is the cause of the severe cold and perpetual snow on the summits of the alpine chains. In the year 1852 four ascents in a balloon took place from the meteorological observatory at Kew, in which the greatest height attained was 22,370 feet. The observations then made by Mr. Welsh furnished Sir John Herschel with data for computing that the temperature of space is minus 239°, that is 239° below the zero point of Fahrenheit, that the limiting temperature of the atmosphere is probably 771⁄2 degrees below that point at the equator, and 1191⁄2 below it at the poles, with a range of temperature from the surface of 1611⁄2° in the former case, and 1191⁄2° in the latter. During these ascents it was found that the temperature of the air decreases uniformly up to a certain point, where it is arrested and remains constant, or increases through a depth of 2000 or 3000 feet, after which it decreases again according to the same law as before. Throughout this zone of constant temperature it either rains, or there is a great fall in the dew point; in short, it is the region of clouds, and the increase of temperature is owing to the latent or absorbed heat set free by the condensation of the aqueous vapour. In the latitude of Kew the cloud region begins at altitudes varying between 2000 and 6500 feet, according to the state of the weather.
Were it not for the effects of temperature on the density of the air, the heights of mountains might be determined by the barometer alone; but as the thermometer must also be consulted, 120the determination becomes more complicated. Mr. Ivory’s method of computing heights from barometrical measurements has the advantage of combining accuracy with the greatest simplicity. Indeed the accuracy with which the heights of mountains can be obtained by this method is very remarkable. Admiral Smyth, R.N., and Sir John Herschel measured the height of Etna by the barometer, without any communication and in different years; Admiral Smyth made it 10,874 feet, and Sir John Herschel 10,873, the difference being only one foot. In consequence of the diminished pressure of the atmosphere water boils at a lower temperature on mountain tops than in the valleys, which induced Fahrenheit to propose this mode of observation as a method of ascertaining their heights. It is very simple, as Professor Forbes ascertained that the temperature of the boiling point varies in arithmetical proportion with the height, or 5495 feet for every degree of Fahrenheit, so that the calculation of height becomes one of arithmetic only, without the use of any table.
The mean pressure of the atmosphere is not the same all over the globe. It is less by 0·24 of an inch at the equator than at the tropics or in the higher latitudes, in consequence of the ascent of heated air and vapour from the surface of the ocean. It is less also on the shores of the Baltic Sea than it is in France, and it was observed by Sir James C. Ross that throughout the whole of the Antarctic Ocean, from 68° to 74° S. latitude, and from 8° to 7° W. longitude, there is a depression of the barometer amounting to an inch and upwards, which is equivalent to an elevation above the sea level of 800 feet. A similar depression was observed by M. Erman in the sea of Ochotzk, and in the adjacent continent of eastern Siberia. Sir John Herschel assigns as the cause of these singular anomalies the great system of circulation of the trade and antetrade winds, in both hemispheres, reacting upon the general mass of the continents as obstacles in their path, which is modified by the configuration of the land.
There are various periodic oscillations in the atmosphere, which, rising and falling like waves in the sea, occasion corresponding changes in the height of the barometer, but they differ as much from the trade-winds, monsoons, and other currents, as the tides of the sea do from the Gulf-stream and other oceanic rivers. 121The sun and moon disturb the equilibrium of the atmosphere by their attraction, and produce annual undulations which have their maximum altitudes at the equinoxes, and their minima at the solstices. There are also lunar tides, which ebb and flow twice in the course of a lunation. The diurnal tides, which accomplish their rise and fall in six hours, are greatly modified by the heat of the sun. Between the tropics the barometer attains its maximum height about nine in the morning, then sinks till three or four in the afternoon; it again rises and attains a second maximum about nine in the evening, and then it begins to fall, and reaches a second minimum at three in the morning, again to pursue the same course. According to M. Bouvard, the amount of the oscillations at the equator is proportional to the temperature, and in other parallels it varies as the temperature and the square of the cosine of the latitude conjointly; consequently it decreases from the equator to the poles, but it is somewhat greater in the day than in the night.
Besides these small undulations, there are vast waves perpetually moving over the continents and oceans in separate and independent systems, being confined to local, yet very extensive districts, probably occasioned by long-continued rains or dry weather over large tracts of country. By numerous barometrical observations made simultaneously in both hemispheres, the courses of several have been traced, some of which occupy twenty-four, and others thirty-six, hours to accomplish their rise and fall. One especially of these vast barometric waves, many hundreds of miles in breadth, has been traced over the greater part of Europe; and not its breadth only, but also the direction of its front and its velocity, have been clearly ascertained. Although, like all other waves, these are but moving forms, yet winds arise dependent on them like tide streams in the ocean. Mr. Birt has determined the periods of other waves of still greater extent and duration, two of which required seventeen days to rise and fall; and another which takes fourteen days to complete its undulation, called by Mr. Birt the November wave, passes annually over the British Islands, probably over the whole of Europe and the seas on its northern coasts. Its crest, which appears to be 6000 miles in extent, moves from N.W. to S.E. at the rate of about 19 miles an hour; while the extent of its barometrical elevation from its trough to its crest is 122seldom less than an inch, sometimes double that quantity. The great crest is preceded and followed at about five days’ interval by two lower ones, and the beginning and end are marked by deep depressions. The researches of M. Leverrier leave no doubt that the great Crimean storm of the 14th November, 1854, was part of this phenomenon,[8] for even a very small difference of atmospheric pressure is sufficient to raise a considerable wind. Since each oscillation has its perfect effect independently of the others, each one is marked by a change in the barometer, and this is beautifully illustrated by curves constructed from a series of observations. The general form of the curve shows the course of the principal wave, while small undulations in its outline mark the maxima and minima of the minor oscillations.
The trade-winds, which are the principal currents in the atmosphere, are only a particular case of those very general laws which regulate the motion of the winds depending on the rarefaction of the air combined with the rotation of the earth on its axis. They are permanent currents of wind between the tropics, blowing to the N.E. on the N. side of the equator, and to the S.E. on the S. side.
If currents of air come from the poles, it is clear that equilibrium must be restored by counter-currents from the equator; moreover, winds coming from the poles, where there is no rotation, to the equator, which revolves from W. to E. at the rate of 1000 miles an hour, must of necessity move in a direction resulting from their own progressive motion and that of rotation; hence, in blowing towards the equator the bias is to the E., and in blowing from it the bias is to the W. Thus as N. and S. winds from the poles blow along the surface from the tropics to the equator, in consequence of this composition of motions that from the N. becomes the N.E. trade-wind, and that from the S. the S.E. trade-wind. Now these winds being in contrary directions cross at the equator, balance each other through about 6 degrees of latitude, and produce a belt of calms of that breadth encircling the globe, known as the calms of the equator, or the Variables of seamen. The heat of the sun rarefies the air so much, that the trade-winds, after crossing at the equator, ascend into the higher regions of the atmosphere, where that from the N. goes to the tropic of Capricorn, and 123that from the S. to the tropic of Cancer. But while travelling in these lofty regions they become cold and heavy, and, sinking to the surface at the tropics, each proceeds to the opposite pole from which it set out. Now, however, they have a greater rotatory motion than the places they successively arrive at, so the bias is to the W., and they become the N.W. and S.W. extra-tropical winds.
If on arriving at the poles the air were to accumulate there, the circulation of the winds would cease; but currents rise into the upper regions, and flow back again to the tropics, where they sink down to fill the vacuum caused by the great precipitation of vapour in these regions, and then flow to the equator as trade-winds (N. 177). So the currents of air cross again at the tropics and produce two belts of calms which surround the globe, named by Lieutenant Maury the Calms of Cancer and the Calms of Capricorn, but generally known to sailors as the Doldrums. Thus the winds go from pole to pole and back again, alternately as under and upper currents. In their circuits the winds cross each other five times, producing regions of calms at the poles, the tropics, and equator. The trade-winds generally extend for about 28° on each side of the equator, but, on account of the greater quantity of land in the northern hemisphere, the N.E. trade-wind is narrower than the S.E.
The sun is perpetually raising enormous quantities of vapour from the ocean which the trade-winds carry to the equator: it is condensed when it rises with the air into the higher strata, and forms a ring of clouds along the southern side of the belt of equatorial calms that surrounds the earth, which, during the day, is perpetually pouring down torrents of rain, while the sun continually beating upon its upper surface dissolves the clouds into invisible vapour which is carried by the winds and condensed into rain on the extra-tropical regions. The whole system of trade-winds, equatorial and tropical calms, with the cloud ring, follow the sun in declination; consequently in its journeys back and forwards it annually travels over 1000 miles of latitude, and regulates the dry and rainy season in the tropical parts of the earth.
The monsoons, which are periodic winds in the Indian Ocean, in part depend upon this movement. For when the sun is in the northern hemisphere the trade-winds come northward with him; 124and when his intense heat expands the air over the Great Gobi and other arid Asiatic deserts, it ascends; the N.E. trade-wind is drawn in to fill the vacuum and ascends with it; then the S.E. trade-wind, being no longer met and balanced by the N.E. trade, passes into the northern hemisphere, and as it proceeds northward from the equator it is deflected to the west by the rotation of the earth, combined with the indraught over the heated deserts, and becomes the S.W. monsoon, which blows while the sun is north of the equator, but as soon as he goes south, and no longer rarefies the air over the Indian deserts, the S.E. trade-wind resumes its usual course, and is then known as the S.E. monsoon. The influence of the heated deserts is perceptible to the distance of 1000 miles from the shore; the monsoons prevail with great steadiness over the Arabian Gulf, the Indian Ocean, and part of the China Sea. At the change, torrents of rain and violent thunderstorms accompany the conflict between the contending winds.
The Sahara desert in North Africa, and those of Utah, Texas, and New Mexico, occasion the monsoons which prevail in the North Atlantic and on both sides of Central America, and the monsoons which blow to the north of Australia show the sterility of the interior, even if other proofs were wanting. From the powerful effect of the land in drawing off the winds from their course, it may be seen why the N.E. trade-winds are narrower than the S.E. trades.
In the extra-tropical winds in the North Atlantic, which blow from the 40th parallel to the pole, the north-westerly are to the easterly as 2 to 1: hence there would be an accumulation of air at the pole at the expense of the equator, did not a current rise at the pole and return to the equator through the high regions of the atmosphere, which confirms the theory of the rotation of the wind.
There are many proofs of the existence of the counter-currents above the trade-winds. On the Peak of Teneriffe the prevailing winds are from the west. Light clouds have frequently been seen moving rapidly from west to east at a very great height above the trade-winds, which were sweeping along the surface of the ocean in a contrary direction. Rains, clouds, and nearly all the other atmospheric phenomena, occur below the height of 18,000 feet, and generally much nearer to the surface of the earth. 125They are owing to currents of air running upon each other in horizontal strata, differing in their electric state, in temperature and moisture, as well as in velocity and direction.
When north and south winds blow alternately, the wind at any place will veer in one uniform direction through every point of the compass, provided the one begins before the other has ceased. In the northern hemisphere a north wind sets out with a smaller degree of rotatory motion than the places have at which it successively arrives, consequently it passes through all the points of the compass from N. to N.E. and E. A current from the south, on the contrary, sets out with a greater rotatory velocity than the places have at which it successively arrives, so by the rotation of the earth it is deflected from S. to S.W. and W. Now, if the vane at any place should have veered from the N. through N.E. to E., and a south wind should spring up, it would combine its motion with the former and cause the vane to turn successively from the E. to S.E. and S. But by the earth’s rotation this south wind will veer to the S.W. and W., and, if a north wind should now arise, it would combine its motion with that of the west, and cause it to veer to the N.W. and N. Thus two alternations of north and south wind will cause the vane at any place to go completely round the compass, from N. to E., S., W., and N. again. At the Royal Observatory at Greenwich the wind accomplishes five circuits in that direction in the course of a year. When circumstances combine to produce alternate north and south winds in the southern hemisphere, the gyration is in the contrary direction. Although the general tendency of the wind may be rotatory, and is so in many instances, at least for part of the year, yet it is so often counteracted by local circumstances, that the winds are in general very irregular, every disturbance in atmospheric equilibrium from heat or any other cause producing a corresponding wind. The most prevalent winds in Europe are the N.E. and S.W.; the former arises from the north polar current, and the latter from causes already mentioned. The law of the wind’s rotation was first described by Dr. Dalton, but has been developed by Professor Dove, of Berlin.
Hurricanes are those storms of wind in which the portion of the atmosphere that forms them revolves in a horizontal circuit round a vertical or somewhat inclined axis of rotation, while the axis itself, and consequently the whole storm, is carried forward 126along the surface of the globe, so that the direction in which the storm is advancing is quite different from the direction in which the rotatory current may be blowing at any point. In the West Indies, where hurricanes are frequent and destructive, they generally originate in the tropical regions near the inner boundary of the trade-winds, and are caused by the vertical ascent of a column of rarefied air, whose place is supplied by a rush of wind from the surrounding regions, set into gyration by the rotation of the earth. By far the greater number of Atlantic hurricanes have begun eastward of the lesser Antilles or Caribbean Islands.
In every case the axis of the storm moves in an elliptical or parabolic curve, having its vertex in or near the tropic of Cancer, which marks the external limit of the trade-winds north of the equator. As the motion before it reaches the tropic is in a straight line from S.E. to N.W., and after it has passed it from S.W. to N.E., the bend of the curve is turned towards Florida and the Carolinas. In the southern hemisphere the body of the storm moves in exactly the opposite direction. The hurricanes which originate south of the equator, and whose initial path is from N.E. to S.W., bend round at the tropic of Capricorn, and then move from N.W. to S.E.
The extent and velocity of these storms are great; for instance, the hurricane that took place on the 12th of August, 1830, was traced from eastward of the Caribbee Islands, along the Gulf Stream, to the bank of Newfoundland, a distance of more than 3000 miles, which it passed over in six days. Although the hurricane of the 1st of September, 1821, was not so extensive, its velocity was greater, as it moved at the rate of 30 miles an hour: small storms are generally more rapid than those of greater dimensions.
The action of these storms seems to be at first confined to the stratum of air nearest the earth, and then they seldom appear to be more than a mile high, though sometimes they are raised higher; or even divided by a mountain into two separate storms, each of which continues its new path and gyrations with increased violence. This occurred in the gale of the 25th of December, 1821, in the Mediterranean, when the Spanish mountains and the Maritime Alps became new centres of motion.
By the friction of the earth the axis of the storm bends a little forward. This causes a continual intermixture of the lower and 127warmer strata of air with those that are higher and colder, producing torrents of rain and violent electric explosions.
The breadth of the whirlwind is greatly augmented when the path of the storm changes on crossing the tropic. The vortex of a storm has covered an extent of the surface of the globe 500 miles in diameter.
The revolving motion accounts for the sudden and violent changes observed during hurricanes. In consequence of the rotation of the air, the wind blows in opposite directions on each side of the axis of the storm, and the violence of the blast increases from the circumference towards the centre of gyration, but in the centre itself the air is in repose: hence, when the body of the storm passes over a place, the wind begins to blow moderately, and increases to a hurricane as the centre of the whirlwind approaches; then, in a moment, a dead and awful calm succeeds, suddenly followed by a renewal of the storm in all its violence, but now blowing in a direction diametrically opposite to its former course. This happened at the Island of St. Thomas on the 2nd of August, 1837, where the hurricane increased in violence till half-past seven in the morning, when perfect stillness took place for forty minutes, after which the storm recommenced in a contrary direction.
The sudden fall of the mercury in the barometer in the regions habitually visited by hurricanes is a certain indication of a coming tempest. In consequence of the centrifugal force of these rotatory storms the air becomes rarefied, and, as the atmosphere is disturbed to some distance beyond the actual circle of gyration or limits of the storm, the barometer often sinks some hours before its arrival, from the original cause of the rotatory disturbance. It continues sinking under the first half of the hurricane, is at a maximum sometimes of two inches in the centre of gyration, and again rises during the passage of the latter half, though it does not attain its greatest height till the storm is over. The diminution of atmospheric pressure is greater and extends over a wider area in the temperate zones than in the torrid, on account of the sudden expansion of the circle of rotation when the gale crosses the tropic.
As the fall of the barometer gives warning of the approach of a hurricane, so the laws of the storm’s motion afford the seaman knowledge to guide him in avoiding it. In the northern 128temperate zone, if the gale begins from the S.E. and veers by S. to W., the ship should steer to the S.E.; but, if the gale begins from the N.E., and changes through N. to N.W., the vessel should go to the N.W. In the northern part of the torrid zone, if the storm begin from the N.E., and veer through E. to S.E., the ship should steer to the N.E.; but, if it begin from the N.W., and veer by W. to S.W., the ship should steer to the S.W., because she is in the south-western side of the storm. Since the laws of storms are reversed in the southern hemisphere, the rules for steering vessels are necessarily reversed also. A heavy swell is peculiarly characteristic of these storms. In the open sea the swell often extends many leagues beyond the range of the gale which produced it.
Waterspouts are occasioned by small whirlwinds, which always have their origin at a great distance from that part of the sea from which the spout begins to rise, where it is generally calm. The whirl is produced by two currents of air, which, running in opposite directions, compress one another by their impetus, so that they rise in spiral eddies to the clouds. They move slowly along the surface of the sea, sometimes in vertical, and sometimes in twisted spirals, putting the sea into violent agitation as they pass, and carrying the water aloft by the force of gyration. Occasionally the eddies begin in the clouds and dip down to the sea.
Sound—Propagation of Sound illustrated by a Field of Standing Corn—Nature of Waves—Propagation of Sound through the Atmosphere—Intensity—Noises—A Musical Sound—Quality—Pitch—Extent of Human Hearing—Velocity of Sound in Air, Water, and Solids—Causes of the Obstruction of Sound—Law of its Intensity—Reflection of Sound—Echoes—Thunder—Refraction of Sound—Interference of Sounds.
One of the most important uses of the atmosphere is the conveyance of sound. Without the air, deathlike silence would prevail through nature, for in common with all substances it has a tendency to impart vibrations to bodies in contact with it. Therefore undulations received by the air, whether it be from a sudden impulse, such as an explosion or the vibrations of a musical chord, are propagated in every direction, and produce the sensation of sound upon the auditory nerves. A bell rung under the exhausted receiver of an air-pump is inaudible, which shows that the atmosphere is really the medium of sound. In the small undulations of deep water in a calm, the vibrations of the liquid particles are made in the vertical plane, that is, up and down, or at right angles to the direction of the transmission of the waves. But the vibrations of the particles of air which produce sound differ from these, being performed in the same direction in which the waves of sound travel. The propagation of sound has been illustrated by a field of corn agitated by the wind. However irregular the motion of the corn may seem on a superficial view, it will be found, if the velocity of the wind be constant, that the waves are all precisely similar and equal, and that all are separated by equal intervals and move in equal times.
A sudden blast depresses each ear equally and successively in the direction of the wind, but, in consequence of the elasticity of the stalks and the force of the impulse, each ear not only rises again as soon as the pressure is removed, but bends back nearly as much in the contrary direction, and then continues to oscillate 130backwards and forwards in equal times, like a pendulum, to a less and less extent, till the resistance of the air puts a stop to the motion. These vibrations are the same for every individual ear of corn. Yet, as their oscillations do not all commence at the same time, but successively, the ears will have a variety of positions at any one instant. Some of the advancing ears will meet others in their returning vibrations, and, as the times of oscillation are equal for all, they will be crowded together at regular intervals. Between these there will occur equal spaces where the ears will be few, in consequence of being bent in opposite directions; and at other equal intervals they will be in their natural upright positions. So that over the whole field there will be a regular series of condensations and rarefactions among the ears of corn, separated by equal intervals, where they will be in their natural state of density. In consequence of these changes the field will be marked by an alternation of bright and dark bands. Thus the successive waves which fly over the corn with the speed of the wind are totally distinct from, and entirely independent of the extent of the oscillations of each individual ear, though both take place in the same direction. The length of a wave is equal to the space between two ears precisely in the same state of motion, or which are moving similarly, and the time of the vibration of each ear is equal to that which elapses between the arrival of two successive waves at the same point. The only difference between the undulations of a corn-field and those of the air which produce sound is, that each ear of corn is set in motion by an external cause, and is uninfluenced by the motion of the rest; whereas in air, which is a compressible and elastic fluid, when one particle begins to oscillate, it communicates its vibrations to the surrounding particles, which transmit them to those adjacent, and so on continually. Hence from the successive vibrations of the particles of air the same regular condensations and rarefactions take place as in the field of corn, producing waves throughout the whole mass of air, though each molecule like each individual ear of corn never moves far from its state of rest. The small waves of a liquid, and the undulations of the air, like waves in the corn, are evidently not real masses moving in the direction in which they are advancing, but merely outlines, motions, or forms passing along, and comprehending all the particles of an undulating fluid which are at once in a 131vibratory state. It is thus that an impulse given to any one point of the atmosphere is successively propagated in all directions, in a wave diverging as from the centre of a sphere to greater and greater distances, but with decreasing intensity, in consequence of the increasing number of particles of inert matter which the force has to move; like the waves formed in still water by a falling stone, which are propagated circularly all around the centre of disturbance (N. 160).
The intensity of sound depends upon the violence and extent of the initial vibrations of air; but, whatever they may be, each undulation when once formed can only be transmitted straight forwards, and never returns back again unless when reflected by an opposing obstacle. The vibrations of the aërial molecules are always extremely small, whereas the waves of sound vary from a few inches to several feet. The various musical instruments, the human voice and that of animals, the singing of birds, the hum of insects, the roar of the cataract, the whistling of the wind, and the other nameless peculiarities of sound, show at once an infinite variety in the modes of aërial vibration, and the astonishing acuteness and delicacy of the ear, thus capable of appreciating the minutest differences in the laws of molecular oscillation.
All mere noises are occasioned by irregular impulses communicated to the ear; and, if they be short, sudden, and repeated beyond a certain degree of quickness, the ear loses the intervals of silence, and the sound appears continuous. Still such sounds will be mere noise: in order to produce a musical sound, the impulses, and consequently the undulations of the air, must be all exactly similar in duration and intensity, and must recur after exactly equal intervals of time. If a blow be given to the nearest of a series of broad, flat, and equidistant palisades, set edgewise in a line direct from the ear, each palisade will repeat or echo the sound; and these echoes, returning to the ear at successive equal intervals of time, will produce a musical note. The quality of a musical note depends upon the abruptness, and its intensity upon the violence and extent of the original impulse. In the theory of harmony the only property of sound taken into consideration is the pitch, which varies with the rapidity of the vibrations. The grave or low tones are produced by very slow vibrations, which increase in frequency as the note becomes more 132acute. The lowest man’s voice makes 396 vibrations in a second, whilst the highest woman’s voice makes 2112. Very deep tones are not heard by all alike, and Dr. Wollaston, who made a variety of experiments on the sense of hearing, found that many people, though not at all deaf, are quite insensible to the cry of the bat or the cricket, while to others it is painfully shrill. From his experiments he concluded that human hearing is limited to about nine octaves, extending from the lowest note of the organ to the highest known cry of insects; and he observes with his usual originality that, “as there is nothing in the nature of the atmosphere to prevent the existence of vibrations incomparably more frequent than any of which we are conscious, we may imagine that animals like the Grylli, whose powers appear to commence nearly where ours terminate, may have the faculty of hearing still sharper sounds which we do not know to exist, and that there may be other insects hearing nothing in common with us, but endowed with a power of exciting, and a sense which perceives vibrations, of the same nature indeed as those which constitute our ordinary sounds, but so remote that the animals which perceive them may be said to possess another sense, agreeing with our own solely in the medium by which it is excited.”
M. Savart, so well known for the number and beauty of his researches in acoustics, has proved that a high note of a given intensity, being heard by some ears and not by others, must not be attributed to its pitch, but to its feebleness. His experiments, and those more recently made by Professor Wheatstone, show that, if the pulses could be rendered sufficiently powerful, it would be difficult to fix a limit to human hearing at either end of the scale. M. Savart had a wheel made about nine inches in diameter with 360 teeth set at equal distances round its rim, so that while in motion each tooth successively hit on a piece of card. The tone increased in pitch with the rapidity of the rotation, and was very pure when the number of strokes did not exceed three or four thousand in a second, but beyond that it became feeble and indistinct. With a wheel of a larger size a much higher tone could be obtained, because, the teeth being wider apart, the blows were more intense and more separated from one another. With 720 teeth on a wheel thirty-two inches in diameter, the sound produced by 12,000 strokes in a second was audible, which corresponds to 24,000 vibrations of a musical 133chord. So that the human ear can appreciate a sound which only lasts the 24,000th part of a second. This note was distinctly heard by M. Savart and by several people who were present, which convinced him that with another apparatus still more acute sounds might be rendered audible.
For the deep tones M. Savart employed a bar of iron, two feet eight inches long, about two inches broad, and half an inch in thickness, which revolved about its centre as if its arms were the spokes of a wheel. When such a machine rotates, it impresses a motion on the air similar to its own, and, when a thin board or card is brought close to its extremities, the current of air is momentarily interrupted at the instant each arm of the bar passes before the card; it is compressed above the card and dilated below; but the instant the spoke has passed a rush of air to restore equilibrium makes a kind of explosion, and, when these succeed each other rapidly, a musical note is produced of a pitch proportional to the velocity of the revolution. When M. Savart turned this bar slowly, a succession of single beats was heard; as the velocity became greater, the sound was only a rattle; but, as soon as it was sufficient to give eight beats in a second, a very deep musical note was distinctly audible corresponding to sixteen single vibrations in a second, which is the lowest that has hitherto been produced. When the velocity of the bar was much increased, the intensity of the sound was hardly bearable. The spokes of a revolving wheel produce the sensation of sound, on the very same principle that a burning stick whirled round gives the impression of a luminous circle. The vibrations excited in the organ of hearing by one beat have not ceased before another impulse is given. Indeed it is indispensable that the impressions made upon the auditory nerves should encroach upon each other in order to produce a full and continued note. On the whole, M. Savart has come to the conclusion, that the most acute sounds would be heard with as much ease as those of a lower pitch, if the duration of the sensation produced by each pulse could be diminished proportionally to the augmentation of the number of pulses in a given time: and on the contrary, if the duration of the sensation produced by each pulse could be increased in proportion to their number in a given time, that the deepest tones would be as audible as any of the others.
The velocity of sound is uniform and independent of the 134nature, extent, and intensity of the primitive disturbance. Consequently sounds of every quality and pitch travel with equal speed. The smallest difference in their velocity is incompatible either with harmony or melody, for notes of different pitches and intensities, sounded together at a little distance, would arrive at the ear in different times. A rapid succession of notes would in this case produce confusion and discord. But, as the rapidity with which sound is transmitted depends upon the elasticity of the medium through which it has to pass, whatever tends to increase the elasticity of the air must also accelerate the motion of sound. On that account its velocity is greater in warm than in cold weather, supposing the pressure of the atmosphere constant. In dry air, at the freezing temperature, sound travels at the rate of 1090 feet in a second, and for any higher temperature one foot must be added for every degree of the thermometer above 32°: hence at 62° of Fahrenheit its speed in a second is 1120 feet, or 765 miles an hour, which is about three-fourths of the diurnal velocity of the earth’s equator. Since all the phenomena of the transmission of sound are simple consequences of the physical properties of the air, they have been predicted and computed rigorously by the laws of mechanics. It was found, however, that the velocity of sound, determined by observation, exceeded what it ought to have been theoretically by 173 feet, or about one-sixth of the whole amount. La Place suggested that this discrepancy might arise from the increased elasticity of the air in consequence of a development of latent or absorbed heat (N. 178) during the undulations of sound, and calculation confirmed the accuracy of his views. The aërial molecules being suddenly compressed give out their absorbed heat; and, as air is too bad a conductor to carry it rapidly off, it occasions a momentary and local rise of temperature, which, increasing the elasticity of the air without at the same time increasing its inertia, causes the movement to be propagated more rapidly. Analysis gives the true velocity of sound in terms of the elevation of temperature that a mass of air is capable of communicating to itself, by the disengagement of its own absorbed heat when suddenly compressed in a given ratio. This change of temperature however could not be obtained directly by any experiments which had been made at that epoch; but by inverting the problem, and assuming the velocity of sound as given by 135experiment, it was computed that the temperature of a mass of air is raised nine-tenths of a degree when the compression is equal to 1⁄116 of its volume.
Probably all liquids are elastic, though considerable force is required to compress them. Water suffers a condensation of nearly 0·0000496 for every atmosphere of pressure, and is consequently capable of conveying sound even more rapidly than air, the velocity in the former being 4708 feet in a second. A person under water hears sounds made in air feebly, but those produced in water very distinctly. According to the experiments of M. Colladon, the sound of a bell was conveyed under water through the Lake of Geneva to the distance of about nine miles. He also perceived that the progress of sound through water is greatly impeded by the interposition of any object, such as a projecting wall; consequently sound under water resembles light in having a distinct shadow. It has much less in air, being transmitted all round buildings or other obstacles, so as to be heard in every direction, though often with a considerable diminution of intensity, as when a carriage turns the corner of a street.
The velocity of sound in passing through solids is in proportion to their hardness, and is much greater than in air or water. A sound which takes some time in travelling through the air passes almost instantaneously along a wire six hundred feet long; consequently it is heard twice—first as communicated by the wire, and afterwards through the medium of the air. The facility with which the vibrations of sound are transmitted along the grain of a log of wood is well known. Indeed they pass through iron, glass, and some kinds of wood, at the rate of 18,530 feet in a second. The velocity of sound is obstructed by a variety of circumstances, such as falling snow, fog, rain, or any other cause which disturbs the homogeneity of the medium through which it has to pass. M. de Humboldt says that it is on account of the greater homogeneity of the atmosphere during the night that sounds are then better heard than during the day, when its density is perpetually changing from partial variations of temperature. His attention was called to this subject on the plain surrounding the Mission of the Apures by the rushing noise of the great cataracts of the Orinoco, which seemed to be three times as loud by night as by day. This he illustrated by experiment. 136A tall glass half full of champagne cannot be made to ring as long as the effervescence lasts. In order to produce a musical note, the glass together with the liquid it contains must vibrate in unison as a system, which it cannot do in consequence of the fixed air rising through the wine and disturbing its homogeneity, because, the vibrations of the gas being much slower than those of the liquid, the velocity of the sound is perpetually interrupted. For the same reason the transmission of sound as well as light is impeded in passing through an atmosphere of variable density. Sir John Herschel, in his admirable Treatise on Sound, thus explains the phenomenon:—“It is obvious,” he says, “that sound as well as light must be obstructed, stifled, and dissipated from its original direction by the mixture of air of different temperatures, and consequently elasticities; and thus the same cause which produces that extreme transparency of the air at night, which astronomers alone fully appreciate, renders it also more favourable to sound. There is no doubt, however, that the universal and dead silence generally prevalent at night renders our auditory nerves sensible to impressions which would otherwise escape notice. The analogy between sound and light is perfect in this as in so many other respects. In the general light of day the stars disappear. In the continual hum of voices, which is always going on by day, and which reach us from all quarters, and never leave the ear time to attain complete tranquillity, those feeble sounds which catch our attention at night make no impression. The ear, like the eye, requires long and perfect repose to attain its utmost sensibility.”
Many instances may be brought in proof of the strength and clearness with which sound passes over the surface of water or ice. Lieutenant Forster was able to carry on a conversation across Port Bowen Harbour, when frozen, a distance of a mile and a half.
The intensity of sound depends upon the extent of the excursions of the fluid molecules, on the energy of the transient condensations and dilatations, and on the greater or less number of particles which experience these effects. We estimate that intensity by the impetus of these fluid molecules on our organs, which is consequently as the square of the velocity, and not by their inertia, which is as the simple velocity. Were the latter 137the case, there would be no sound, because the inertia of the receding waves of air would destroy the equal and opposite inertia of those advancing; whence it may be concluded that the intensity of sound diminishes inversely as the square of the distance from its origin. In a tube, however, the force of sound does not decay as in open air, unless perhaps by friction against the sides. M. Biot found, from a number of highly-interesting experiments made on the pipes of the aqueducts in Paris, that a continued conversation could be carried on in the lowest possible whisper through a cylindrical tube about 3120 feet long, the time of transmission through that space being 2·79 seconds. In most cases sound diverges in all directions so as to occupy at any one time a spherical surface; but Dr. Young has shown that there are exceptions, as, for example, when a flat surface vibrates only in one direction. The sound is then most intense when the ear is at right angles to the surface, whereas it is scarcely audible in a direction precisely perpendicular to its edge. In this case it is impossible that the whole of the surrounding air can be affected in the same manner, since the particles behind the sounding surface must be moving towards it whenever the particles before it are retreating. Hence in one half of the surrounding sphere of air its motions are retrograde, while in the other half they are direct; consequently, at the edges where these two portions meet, the motions of the air will neither be retrograde nor direct, and therefore it must be at rest.
It appears, from theory as well as daily experience, that sound is capable of reflection from surfaces (N. 179) according to the same laws as light. Indeed any one who has observed the reflection of the waves from a wall on the side of a river, after the passage of a steam-boat, will have a perfect idea of the reflection of sound and of light. As every substance in nature is more or less elastic, it may be agitated according to its own law by the impulse of a mass of undulating air; and reciprocally the surface by its reaction will communicate its undulations back again into the air. Such reflections produce echoes; and as a series of them may take place between two or more obstacles, each will cause an echo of the original sound, growing fainter and fainter till it dies away; because sound, like light, is weakened by reflection. Should the reflecting surface be concave towards a person, the sound will converge towards him with increased intensity, 138which will be greater still if the surface be spherical and concentric with him. Undulations of sound diverging from one focus of an elliptical shell (N. 180) converge in the other after reflection. Consequently a sound from the one will be heard in the other as if it were close to the ear. The rolling noise of thunder has been attributed to reverberation between different clouds, which may possibly be the case to a certain extent. Sir John Herschel is of opinion that an intensely prolonged peal is probably owing to a combination of sounds, because, the velocity of electricity being incomparably greater than that of sound, the thunder may be regarded as originating in every point of a flash of lightning at the same instant. The sound from the nearest point will arrive first; and if the flash run in a direct line from a person, the noise will come later and later from the remote points of its path in a continued roar. Should the direction of the flash be inclined, the succession of sounds will be more rapid and intense: and if the lightning describe a circular curve round a person, the sound will arrive from every point at the same instant with a stunning crash. In like manner the subterranean noises heard during earthquakes like distant thunder may arise from the consecutive arrival at the ear of undulations propagated at the same instant from nearer and more remote points; or if they originate in the same point, the sound may come by different routes through strata of different densities.
Sounds under water are heard very distinctly in the air immediately above; but the intensity decays with great rapidity as the observer goes farther off, and is altogether inaudible at the distance of two or three hundred yards. So that waves of sound, like those of light, in passing from a dense to a rare medium, are not only refracted, but suffer total reflection at very oblique incidences (N. 189).
The laws of interference extend also to sound. It is clear that two equal and similar musical strings will be in unison if they communicate the same number of vibrations to the air in the same time. But if two such strings be so nearly in unison that one performs a hundred vibrations in a second, and the other a hundred and one in the same period—during the first few vibrations the two resulting sounds will combine to form one of double the intensity of either, because the aërial waves will sensibly coincide in time and place; but one will gradually gain 139on the other till at the fiftieth vibration it will be half an oscillation in advance. Then the waves of air which produce the sound being sensibly equal, but the receding part of the one coinciding with the advancing part of the other, they will destroy one another, and occasion an instant of silence. The sound will be renewed immediately after, and will gradually increase till the hundredth vibration, when the two waves will combine to produce a sound double the intensity of either. These intervals of silence and greatest intensity, called beats, will recur every second; but if the notes differ much from one another, the alternations will resemble a rattle; and if the strings be in perfect unison, there will be no beats, since there will be no interference. Thus by interference is meant the co-existence of two undulations in which the lengths of the waves are the same. And as the magnitude of an undulation may be diminished by the addition of another transmitted in the same direction, it follows that one undulation may be absolutely destroyed by another when waves of the same length are transmitted in the same direction, provided that the maxima of the undulations are equal, and that one follows the other by half the length of a wave. A tuning-fork affords a good example of interference. When that instrument vibrates, its two branches alternately recede from and approach one another; each communicates its vibrations to the air, and a musical note is the consequence. If the fork be held upright about a foot from the ear, and turned round its axis while vibrating, at every quarter revolution the sound will scarcely be heard, while at the intermediate points it will be strong and clear. This phenomenon arises from the interference of the undulations of air coming from the two branches of the fork. When the two branches coincide, or when they are at equal distances from the ear, the waves of air combine to reinforce each other; but at the quadrants, where the two branches are at unequal distances from the ear, the lengths of the waves differ by half an undulation, and consequently destroy one another.
Vibration of Musical Strings—Harmonic Sounds—Nodes—Vibration of Air in Wind-Instruments—Vibration of Solids—Vibrating Plates—Bells—Harmony—Sounding Boards—Forced Vibrations—Resonance—Speaking Machines.
When the particles of elastic bodies are suddenly disturbed by an impulse, they return to their natural position by a series of isochronous vibrations, whose rapidity, force, and permanency depend upon the elasticity, the form, and the mode of aggregation which unites the particles of the body. These oscillations are communicated to the air, and on account of its elasticity they excite alternate condensations and dilatations in the strata of the fluid nearest to the vibrating body; from thence they are propagated to a distance. A string or wire stretched between two pins, when drawn aside and suddenly let go, will vibrate till its own rigidity and the resistance of the air reduce it to rest. These oscillations may be rotatory, in every plane, or confined to one plane according as the motion is communicated. In the piano-forte, where the strings are struck by a hammer at one extremity, the vibrations probably consist of a bulge running to and fro from end to end. Different modes of vibration may be obtained from the same sonorous body. Suppose a vibrating string to give the lowest C of the pianoforte which is the fundamental note of the string; if it be lightly touched exactly in the middle, so as to retain that point at rest, each half will then vibrate twice as fast as the whole, but in opposite directions; the ventral or bulging segments will be alternately above and below the natural position of the string, and the resulting note will be the octave above C. When a point at a third of the length of the string is kept at rest, the vibrations will be three times as fast as those of the whole string, and will give the twelfth above C. When the point of rest is one-fourth of the whole, the oscillations will be four times as fast as those of the fundamental note, and will give the double octave; and so on. These acute sounds are called 141the harmonics of the fundamental note. It is clear, from what has been stated, that the string thus vibrating could not give these harmonics spontaneously unless it divided itself at its aliquot parts into two, three, four, or more segments in opposite states of vibration separated by points actually at rest. In proof of this, pieces of paper placed on the string at the half, third, fourth, or other aliquot points, according to the corresponding harmonic sound, will remain on it during its vibration, but will instantly fly off from any of the intermediate points. The points of rest, called the nodal points of the string, are a mere consequence of the law of interferences; for, if a rope fastened at one end be moved to and fro at the other extremity so as to transmit a succession of equal waves along it, they will be successively reflected when they arrive at the other end of the rope by the fixed point, and in returning they will occasionally interfere with the advancing waves; and, as these opposite undulations will at certain points destroy one another, the point of the rope in which this happens will remain at rest. Thus a series of nodes and ventral segments will be produced whose number will depend upon the tension and the frequency of the alternate motions communicated to the moveable end. So, when a string fixed at both ends is put in motion by a sudden blow at any point of it, the primitive impulse divides itself into two pulses running opposite ways, which are each totally reflected at the extremities, and, running back again along the whole length, are again reflected at the other ends. And thus they will continue to run backwards and forwards, crossing one another at each traverse, and occasionally interfering, so as to produce nodes; so that the motion of a string fastened at both ends consists of a wave or pulse continually doubled back on itself by reflection at the fixed extremities.
Harmonics generally co-exist with the fundamental sound in the same vibrating body. If one of the lowest strings of the pianoforte be struck, an attentive ear will not only hear the fundamental note, but will detect all the others sounding along with it, though with less and less intensity as their pitch becomes higher. According to the law of co-existing undulations, the whole string and each of its aliquot parts are in different and independent states of vibration at the same time; and as all the resulting notes are heard simultaneously, not only the air, but 142the ear also, vibrates in unison with each at the same instant (N. 181).
Harmony consists in an agreeable combination of sounds. When two chords perform their vibrations in the same time, they are in unison; but, when their vibrations are so related as to have a common period, after a few oscillations they produce concord. Thus, when the vibrations of two strings bear a very simple relation to each other, as where one of them makes two, three, four, &c., vibrations in the time the other makes one; or, if it accomplishes three, four, &c., vibrations while the other makes two, the result is a concord which is the more perfect the shorter the common period. In discords, on the contrary, the beats are distinctly audible, which produces a disagreeable and harsh effect, because the vibrations do not bear a simple relation to one another, as where one of two strings makes eight vibrations while the other accomplishes fifteen. The pleasure afforded by harmony is attributed by Dr. Young to the love of order, and to a predilection for a regular repetition of sensations natural to the human mind, which is gratified by the perfect regularity and rapid recurrence of the vibrations. The love of poetry and dancing he conceives to arise in some degree from the rhythm of the one and the regularity of the motions in the other.
A blast of air passing over the open end of a tube, as over the reeds in Pan’s pipes; over a hole in one side, as in the flute; or through the aperture called a reed, with a flexible tongue, as in the clarinet, puts the internal column of air into longitudinal vibrations by the alternate condensations and rarefactions of its particles. At the same time the column spontaneously divides itself into nodes, between which the air also vibrates longitudinally, but with a rapidity inversely proportional to the length of the divisions, giving the fundamental note or one of its harmonics. The nodes are produced on the principle of interferences by the reflection of the longitudinal undulations of the air at the ends of the pipe, as in the musical string, only that in one case the undulations are longitudinal, and in the other transverse.
A pipe, either open or shut at both ends, when sounded, vibrates entire, or divides itself spontaneously into two, three, four, &c., segments separated by nodes. The whole column gives the fundamental note by waves or vibrations of the same length with the pipe. The first harmonic is produced by waves 143half as long as the tube, the second harmonic by waves a third as long, and so on. The harmonic segments in an open and shut pipe are the same in number, but differently placed. In a shut pipe the two ends are nodes, but in an open pipe there is half a segment at each extremity, because the air at these points is neither rarefied nor condensed, being in contact with that which is external. If one of the ends of the open pipe be closed, its fundamental note will be an octave lower: the air will now divide itself into three, five, seven, &c., segments; and the wave producing its fundamental note will be twice as long as the pipe, so that it will be doubled back (N. 182). All these notes may be produced separately by varying the intensity of the blast. Blowing steadily and gently, the fundamental note will sound; when the force of the blast is increased the note will all at once start up an octave; when the intensity of the wind is augmented the twelfth will be heard; and, by continuing to increase the force of the blast, the other harmonics may be obtained, but no force of wind will produce a note intermediate between these. The harmonics of a flute may be obtained in this manner, from the lowest C or D upwards, without altering the fingering, merely by increasing the intensity of the blast and altering the form of the lips. Pipes of the same dimensions, whether of lead, glass, or wood, give the same tone as to pitch under the same circumstances, which shows that the air alone produces the sound.
Metal springs fastened at one end, when forcibly bent, endeavour to return to rest by a series of vibrations, which give very pleasing tones, as in musical boxes. Various musical instruments have been constructed, consisting of metallic springs thrown into vibration by a current of air. Among the most perfect of these are Mr. Wheatstone’s Symphonion, Concertina, and Æolian Organ, instruments of different effects and capabilities, but all possessing considerable execution and expression.
The Syren is an ingenious instrument, devised by M. Cagniard de la Tour, for ascertaining the number of pulsations in a second, corresponding to each pitch: the notes are produced by jets of air passing through small apertures, arranged at regular distances in a circle on the side of a box, before which a disc revolves pierced with the same number of holes. During a revolution of the disc the currents are alternately intercepted and allowed to 144pass as many times as there are apertures in it, and a sound is produced whose pitch depends on the velocity of rotation.
A glass or metallic rod, when struck at one end, or rubbed in the direction of its length with a wet finger, vibrates longitudinally, like a column of air, by the alternate condensation and expansion of its constituent particles, producing a clear and beautiful musical note of a high pitch, on account of the rapidity with which these substances transmit sound. Rods, surfaces, and, in general, all undulating bodies, resolve themselves into nodes. But in surfaces the parts which remain at rest during their vibrations are lines which are curved or plane according to the substance, its form, and the mode of vibration. If a little fine dry sand be strewed over the surface of a plate of glass or metal, and if undulations be excited by drawing the bow of a violin across its edge, it will emit a musical sound, and the sand will immediately arrange itself in the nodal lines, where alone it will accumulate and remain at rest, because the segments of the surface on each side will be in different states of vibration, the one being elevated while the other is depressed; and, as these two motions meet in the nodal lines, they neutralise one another. These lines vary in form and position with the part where the bow is drawn across, and the point by which the plate is held. The motion of the sand shows in what direction the vibrations take place. If they be perpendicular to the surface, the sand will be violently tossed up and down till it finds the points of rest. If they be tangential, the sand will only creep along the surface to the nodal lines. Sometimes the undulations are oblique, or compounded of both the preceding. If a bow be drawn across one of the angles of a square plate of glass or metal held firmly by the centre, the sand will arrange itself in two straight lines parallel to the sides of the plate, and crossing in the centre so as to divide it into four equal squares, whose motions will be contrary to each other. Two of the diagonal squares will make their excursions on one side of the plate, while the other two make their vibrations on the other side of it. This mode of vibration produces the lowest tone of the plate (N. 183). If the plate be still held by the centre, and the bow applied to the middle of one of the sides, the vibrations will be more rapid, and the tone will be a fifth higher than in the preceding case: now the sand will arrange itself from corner to corner, and will 145divide the plate into four equal triangles, each pair of which will make their excursions on opposite sides of the plate. The nodal lines and pitch vary not only with the point where the bow is applied, but with the point by which the plate is held, which being at rest necessarily determines the direction of one of the quiescent lines. The forms assumed by the sand in square plates are very numerous, corresponding to all the various modes of vibration. The lines in circular plates are even more remarkable for their symmetry, and upon them the forms assumed by the sand may be classed in three systems. The first is the diametrical system, in which the figures consist of diameters dividing the circumference of the plate into equal parts, each of which is in a different state of vibration from those adjacent. Two diameters, for example, crossing at right angles, divide the circumference into four equal parts; three diameters divide it into six equal parts; four divide it into eight, and so on. In a metallic plate, these divisions may amount to thirty-six or forty. The next is the concentric system, where the sand arranges itself in circles, having the same centre with the plate; and the third is the compound system, where the figures assumed by the sand are compounded of the other two, producing very complicated and beautiful forms. Galileo seems to have been the first to notice the points of rest and motion in the sounding-board of a musical instrument; but to Chladni is due the whole discovery of the symmetrical forms of the nodal lines in vibrating plates (N. 184). Professor Wheatstone has shown, in a paper read before the Royal Society in 1833, that all Chladni’s figures, and indeed all the nodal figures of vibrating surfaces, result from very simple modes of vibration oscillating isochronously, and superposed upon each other; the resulting figure varying with the component modes of vibration, the number of the superpositions, and the angles at which they are superposed. For example, if a square plate be vibrating so as to make the sand arrange itself in straight lines parallel to one side of the plate, and if, in addition to this, such vibrations be excited as would have caused the sand to form in lines perpendicular to the first had the plate been at rest, the combined vibrations will make the sand form in lines from corner to corner (N. 185).
M. Savart’s experiments on the vibrations of flat glass rulers are highly interesting. Let a lamina of glass 27in·56 long, 0·59 146of an inch broad, and 0·06 of an inch in thickness, be held by the edges in the middle, with its flat surface horizontal. If this surface be strewed with sand, and set in longitudinal vibration by rubbing its under surface with a wet cloth, the sand on the upper surface will arrange itself in lines parallel to the ends of the lamina, always in one or other of two systems (N. 186). Although the same one of the two systems will always be produced by the same plate of glass, yet among different plates of the preceding dimensions, even though cut from the same sheet side by side, one will invariably exhibit one system, and the other the other, without any visible reason for the difference. Now, if the positions of these quiescent lines be marked on the upper surface, and if the plate be turned so that the lower surface becomes the upper one, the sand being strewed, and vibrations excited as before, the nodal lines will still be parallel to the ends of the lamina, but their positions will be intermediate between those of the upper surface (N. 187). Thus it appears that all the motions of one half of the thickness of the lamina, or ruler, are exactly contrary to those of the corresponding points of the other half. If the thickness of the lamina be increased, the other dimensions remaining the same, the sound will not vary, but the number of nodal lines will be less. When the breadth of the lamina exceeds the 0·6 of an inch, the nodal lines become curved, and are different on the two surfaces. A great variety of forms are produced by increasing the breadth and changing the form of the surface; but in all it appears that the motions in one half of the thickness are opposed to those in the other half.
M. Savart also found, by placing small paper rings round a cylindrical tube or rod, so as to rest upon it at one point only, that, when the tube or rod is continually turned on its axis in the same direction, the rings slide along during the vibrations, till they come to a quiescent point, where they rest. By tracing these nodal lines he discovered that they twist in a spiral or corkscrew round rods and cylinders, making one or more turns according to the length; but at certain points, varying in number according to the mode of vibration of the rod, the screw stops, and recommences on the other side, though it is turned in a contrary direction; that is, on one side it is a right-handed screw, on the other a left (N. 188). The nodal lines in the 147interior surface of the tube are perfectly similar to those in the exterior, but they occupy intermediate positions. If a small ivory ball be put within the tube, it will follow these nodal lines when the tube is made to revolve on its axis.
All solids which ring when struck, such as bells, drinking glasses, gongs, &c., have their shape momentarily and forcibly changed by the blow, and from their elasticity, or tendency to resume their natural form, a series of undulations take place, owing to the alternate condensations and rarefactions of the particles of solid matter. These have also their harmonic tones, and consequently nodes. Indeed, generally, when a rigid system of any form whatever vibrates either transversely or longitudinally, it divides itself into a certain number of parts which perform their vibrations without disturbing one another. These parts are at every instant in alternate states of undulation; and, as the points or lines where they join partake of both, they remain at rest, because the opposing motions destroy one another.
The air, notwithstanding its rarity, is capable of transmitting its undulations when in contact with a body susceptible of admitting and exciting them. It is thus that sympathetic undulations are excited by a body vibrating near insulated tended strings, capable of following its undulations, either by vibrating entire, or by separating themselves into their harmonic divisions. If two chords equally stretched, of which one is twice or three times longer than the other, be placed side by side, and if the shorter be sounded, its vibrations will be communicated by the air to the other, which will be thrown into such a state of vibration that it will be spontaneously divided into segments equal in length to the shorter string. When a tuning-fork receives a blow and is made to rest upon a piano-forte during its vibration, every string which, either by its natural length or by its spontaneous subdivisions, is capable of executing corresponding vibrations, responds in a sympathetic note. The same effect will be produced by the stroke of a bell near a piano or harp. Some one or other of the notes of an organ are generally in unison with one of the panes or with the whole sash of a window, which consequently resounds when those notes are sounded. A peal of thunder has frequently the same effect. The sound of very large organ-pipes is generally inaudible till the air be set in 148motion by the undulations of some of the superior accords, and then the sound becomes extremely energetic. Recurring vibrations occasionally influence each other’s periods. For example, two adjacent organ-pipes nearly in unison may force themselves into concord; and two clocks, whose rates differed considerably when separate, have been known to beat together when fixed to the same wall, and one clock has forced the pendulum of another into motion, when merely standing on the same stone pavement. These forced oscillations, which correspond in their periods with those of the exciting cause, are to be traced in every department of physical science. Several instances of them have already occurred in this work. Such are the tides, which follow the sun and moon in all their motions and periods. The nutation of the earth’s axis also, which corresponds with the period, and represents the motion of the nodes of the moon, is again reflected back to the moon, and may be traced in the nutation of the lunar orbit. And, lastly, the acceleration of the moon’s mean motion represents the action of the planets on the earth reflected by the sun to the moon.
In consequence of the facility with which the air communicates undulations, all the phenomena of vibrating plates may be exhibited by sand strewed on paper or parchment, stretched over a harmonica glass or large bell-shaped tumbler. In order to give due tension to the paper or vellum, it must be wetted, stretched over the glass, gummed round the edges, allowed to dry, and varnished over, to prevent changes in its tension from the humidity of the atmosphere. If a circular disc of glass be held concentrically over this apparatus, with its plane parallel to the surface of the paper, and set in vibration by drawing a bow across its edge, so as to make sand on its surface take any of Chladni’s figures, the sand on the paper will assume the very same form, in consequence of the vibrations of the disc being communicated to the paper by the air. When the disc is removed slowly in a horizontal direction, the forms on the paper will correspond with those on the disc, till the distance is too great for the air to convey the vibrations. If the disc while vibrating be gradually more and more inclined to the horizon, the figures on the paper will vary by degrees; and, when the vibrating disc is perpendicular to the horizon, the sand on the paper will form into straight lines parallel to the surface of the 149disc, by creeping along it instead of dancing up and down. If the disc be made to turn round its vertical diameter while vibrating, the nodal lines on the paper will revolve, and exactly follow the motion of the disc. It appears, from this experiment, that the motions of the aërial molecules in every part of a spherical wave, propagated from a vibrating body as a centre, are parallel to each other, and not divergent like the radii of a circle. When a slow air is played on a flute near this apparatus, each note calls up a particular form in the sand, which the next note effaces, to establish its own. The motion of the sand will even detect sounds that are inaudible. By the vibrations of sand on a drum-head the besieged have discovered the direction in which a counter-mine was working. M. Savart, who made these beautiful experiments, employed this apparatus to discover nodal lines in masses of air. He found that the air of a room, when thrown into undulations by the continued sound of an organ-pipe, or by any other means, divides itself into masses separated by nodal curves of double curvature, such as spirals, on each side of which the air is in opposite states of vibration. He even traced these quiescent lines going out at an open window, and for a considerable distance in the open air. The sand is violently agitated where the undulations of the air are greatest, and remains at rest in the nodal lines. M. Savart observed, that when he moved his head away from a quiescent line towards the right the sound appeared to come from the right, and when he moved it towards the left the sound seemed to come from the left, because the molecules of air are in different states of motion on each side of the quiescent line.
A musical string gives a very feeble sound when vibrating alone, on account of the small quantity of air set in motion; but when attached to a sounding-board, as in the harp and piano-forte, it communicates its undulations to that surface, and from thence to every part of the instrument; so that the whole system vibrates isochronously, and by exposing an extensive undulating surface, which transmits its undulations to a great mass of air, the sound is much reinforced. The intensity is greatest when the vibrations of the string or sounding body are perpendicular to the sounding-board, and least when they are in the same plane with it. The sounding-board of the piano-forte is better disposed than that of any other stringed instrument, because the 150hammers strike the strings so as to make them vibrate at right angles to it. In the guitar, on the contrary, they are struck obliquely, which renders the tone feeble, unless when the sides, which also act as a sounding-board, are deep. It is evident that the sounding-board and the whole instrument are agitated at once by all the superposed vibrations excited by the simultaneous or consecutive notes that are sounded, each having its perfect effect independently of the rest. A sounding-board not only reciprocates the different degrees of pitch, but all the nameless qualities of tone. This has been beautifully illustrated by Professor Wheatstone in a series of experiments on the transmission through solid conductors of musical performances, from the harp, piano, violin, clarinet, &c. He found that all the varieties of pitch, quality, and intensity are perfectly transmitted with their relative gradations, and may be communicated, through conducting wires or rods of very considerable length, to a properly disposed sounding-board in a distant apartment. The sounds of an entire orchestra may be transmitted and reciprocated by connecting one end of a metallic rod with a sounding-board near the orchestra, so placed as to resound to all the instruments, and the other end with the sounding-board of a harp, piano, or guitar, in a remote apartment. Professor Wheatstone observes, “The effect of this experiment is very pleasing; the sounds, indeed, have so little intensity as scarcely to be heard at a distance from the reciprocating instrument; but, on placing the ear close to it, a diminutive band is heard in which all the instruments preserve their distinctive qualities, and the pianos and fortes, the crescendos and diminuendos, their relative contrasts. Compared with an ordinary band heard at a distance through the air, the effect is as a landscape seen in miniature beauty through a concave lens, compared with the same scene viewed by ordinary vision through a murky atmosphere.”
Every one is aware of the reinforcement of sound by the resonance of cavities. When singing or speaking near the aperture of a wide-mouthed vessel, the intensity of some one note in unison with the air in the cavity is often augmented to a great degree. Any vessel will resound if a body vibrating the natural note of the cavity be placed opposite to its orifice, and be large enough to cover it, or at least to set a large portion of the adjacent air in motion. For the sound will be alternately reflected 151by the bottom of the cavity and the undulating body at its mouth. The first impulse of the undulating substance will be reflected by the bottom of the cavity, and then by the undulating body, in time to combine with the second new impulse. This reinforced sound will also be twice reflected in time to conspire with the third new impulse; and, as the same process will be repeated on every new impulse, each will combine with all its echoes to reinforce the sound prodigiously. Professor Wheatstone, to whose ingenuity we are indebted for so much new and valuable information on the theory of sound, has given some very striking instances of resonance. If one of the branches of a vibrating tuning-fork be brought near the embouchure of a flute, the lateral apertures of which are stopped so as to render it capable of producing the same sound as the fork, the feeble and scarcely audible sound of the fork will be augmented by the rich resonance of the column of air within the flute, and the tone will be full and clear. The sound will be found greatly to decrease by closing or opening another aperture; for the alteration in the length of the column of air renders it no longer fit perfectly to reciprocate the sound of the fork. This experiment may be made on a concert flute with a C tuning-fork. But Professor Wheatstone observes, that in this case it is generally necessary to finger the flute for B, because, when blown into with the mouth, the under-lip partly covers the embouchure, which renders the sound about a semitone flatter than it would be were the embouchure entirely uncovered. He has also shown, by the following experiment, that any one among several simultaneous sounds may be rendered separately audible. If two bottles be selected, and tuned by filling them with such a quantity of water as will render them unisonant with two tuning-forks which differ in pitch, on bringing both of the vibrating tuning-forks to the mouth of each bottle alternately, in each case that sound only will be heard which is reciprocated by the unisonant bottle.
Several attempts have been made to imitate the articulation of the letters of the alphabet. About the year 1779, MM. Kratzenstein of St. Petersburg, and Kempelen of Vienna, constructed instruments which articulated many letters, words, and even sentences. Mr. Willis of Cambridge has adapted cylindrical tubes to a reed, whose length can be varied at pleasure by sliding 152joints. Upon drawing out a tube while a column of air from the bellows of an organ is passing through it, the vowels are pronounced in the order, i, e, a, o, u. On extending the tube, they are repeated after a certain interval, in the inverted order, u, o, a, e, i. After another interval they are again obtained in the direct order, and so on. When the pitch of the reed is very high, it is impossible to sound some of the vowels, which is in perfect correspondence with the human voice, female singers being unable to pronounce u and o in their high notes. From the singular discoveries of M. Savart on the nature of the human voice, and the investigations of Mr. Willis on the mechanism of the larynx, it may be presumed that ultimately the utterance or pronunciation of modern languages will be conveyed, not only to the eye, but also to the ear of posterity. Had the ancients possessed the means of transmitting such definite sounds, the civilised world would still have responded in sympathetic notes at the distance of many ages.
Refraction—Astronomical Refraction and its Laws—Formation of Tables of Refraction—Terrestrial Refraction—Its Quantity—Instances of extraordinary Refraction—Reflection—Instances of extraordinary Reflection—Loss of Light by the Absorbing Power of the Atmosphere—Apparent Magnitude of Sun and Moon in the Horizon.
Not only everything we hear but all we see is through the medium of the atmosphere. Without some knowledge of its action upon light, it would be impossible to ascertain the position of the heavenly bodies, or even to determine the exact place of very distant objects upon the surface of the earth; for, in consequence of the refractive power of the air, no distant object is seen in its true position.
All the celestial bodies appear to be more elevated than they really are; because the rays of light, instead of moving through the atmosphere in straight lines, are continually inflected towards the earth. Light passing obliquely out of a rare into a denser medium, as from vacuum into air, or from air into water, is bent or refracted from its course towards a perpendicular to that point of the denser surface where the light enters it (N. 189). In the same medium, the sine of the angle contained between the incident ray and the perpendicular is in a constant ratio to the sine of the angle contained by the refracted ray and the same perpendicular; but this ratio varies with the refracting medium. The denser the medium, the more the ray is bent. The barometer shows that the density of the atmosphere decreases as the height above the earth increases. Direct experiments prove that the refractive power of the air increases with its density. It follows therefore that, if the temperature be uniform, the refractive power of the air is greatest at the earth’s surface, and diminishes upwards.
A ray of light from a celestial object falling obliquely on this variable atmosphere, instead of being refracted at once from its course, is gradually more and more bent during its passage through it so as to move in a vertical curved line, in the same 154manner as if the atmosphere consisted of an infinite number of strata of different densities. The object is seen in the direction of a tangent to that part of the curve which meets the eye; consequently the apparent altitude (N. 190) of the heavenly bodies is always greater than their true altitude. Owing to this circumstance, the stars are seen above the horizon after they are set, and the day is lengthened from a part of the sun being visible, though he really is behind the rotundity of the earth. It would be easy to determine the direction of a ray of light through the atmosphere if the law of the density were known; but, as this law is perpetually varying with the temperature, the case is very complicated. When rays pass perpendicularly from one medium into another, they are not bent; and experience shows, that in the same surface, though the sines of the angles of incidence and refraction retain the same ratio, the refraction increases with the obliquity of incidence (N. 189). Hence it appears that the refraction is greatest at the horizon, and at the zenith there is none. But it is proved that, at all heights above ten degrees, refraction varies nearly as the tangent of the angular distance of the object from the zenith, and wholly depends upon the heights of the barometer and thermometer. For the quantity of refraction at the same distance from the zenith varies nearly as the height of the barometer, the temperature being constant; and the effect of the variation of temperature is to diminish the quantity of refraction by about its 480th part for every degree in the rise of Fahrenheit’s thermometer. Not much reliance can be placed on celestial observations, within less than ten or twelve degrees of the horizon, on account of irregular variations in the density of the air near the surface of the earth, which are sometimes the cause of very singular phenomena. The humidity of the air produces no sensible effect on its refractive power; and it has been proved that the amount of refraction is the same whatever be the velocity of the incident light, that is whether the light comes from a star in that part of the heavens towards which the earth is going, or from one in that part of the sky whence it is receding.
Bodies, whether luminous or not, are only visible by the rays which proceed from them. As the rays must pass through strata of different densities in coming to us, it follows that, with the exception of stars in the zenith, no object either in or beyond our 155atmosphere is seen in its true place. But the deviation is so small in ordinary cases that it causes no inconvenience, though in astronomical and trigonometrical observations due allowance must be made for the effects of refraction. Dr. Bradley’s tables of refraction were formed by observing the zenith distances of the sun at his greatest declinations, and the zenith distances of the pole-star above and below the pole. The sum of these four quantities is equal to 180°, diminished by the sum of the four refractions, whence the sum of the four refractions was obtained; and, from the law of the variation of refraction determined by theory, he assigned the quantity due to each altitude (N. 191). The mean horizontal refraction is about 35ʹ 6ʺ, and at the height of forty-five degrees it is 58ʺ·36. The effect of refraction upon the same star above and below the pole was noticed by Alhazen, a Saracen astronomer of Spain, in the ninth century; but its existence was known to Ptolemy in the second, though he was ignorant of its quantity.
The refraction of a terrestrial object is estimated differently from that of a celestial body. It is measured by the angle contained between the tangent to the curvilineal path of the ray where it meets the eye, and the straight line joining the eye and the object (N. 192). Near the earth’s surface the path of the ray may be supposed to be circular; and the angle at the centre of the earth corresponding to this path is called the horizontal angle. The quantity of terrestrial refraction is obtained by measuring contemporaneously the elevation of the top of a mountain above a point in the plain at its base, and the depression of that point below the top of the mountain. The distance between these two stations is the chord of the horizontal angle; and it is easy to prove that double the refraction is equal to the horizontal angle, increased by the difference between the apparent elevation and the apparent depression. Whence it appears that, in the mean state of the atmosphere, the refraction is about the fourteenth part of the horizontal angle.
Some very singular appearances occur from the accidental expansion or condensation of the strata of the atmosphere contiguous to the surface of the earth, by which distant objects, instead of being elevated, are depressed. Sometimes, being at once both elevated and depressed, they appear double, one of the images being direct, and the other inverted. In consequence of 156the upper edges of the sun and moon being less refracted than the lower, they often appear to be oval when near the horizon. The looming also or elevation of coasts, mountains, and ships, when viewed across the sea, arises from unusual refraction. A friend of the author’s, while standing on the plains of Hindostan, saw the whole upper chain of the Himalaya Mountains start into view, from a sudden change in the density of the air, occasioned by a heavy shower after a very long course of dry and hot weather. Single and double images of objects at sea, arising from sudden changes of temperature which are not so soon communicated to the water on account of its density as to the air, occur more rarely and are of shorter duration than similar appearances on land. In 1818 Captain Scoresby, whose observations on the phenomena of the polar seas are so valuable, recognised his father’s ship by its inverted image in the air, although the vessel itself was below the horizon. He afterwards found that she was seventeen miles beyond the horizon, and thirty miles distant. Two images are sometimes seen suspended in the air over a ship, one direct and the other inverted, with their topmasts or their hulls meeting, according as the inverted image is above or below the direct image (N. 193). Dr. Wollaston has proved that these appearances are owing to the refraction of the rays through media of different densities, by the very simple experiment of looking along a red-hot poker at a distant object. Two images are seen, one direct and another inverted, in consequence of the change induced by the heat in the density of the adjacent air. He produced the same effect by a saline or saccharine solution with water and spirit of wine floating upon it (N. 194).
Many of the phenomena that have been ascribed to extraordinary refraction seem to be occasioned by a partial or total reflection of the rays of light at the surfaces of strata of different densities (N. 189). It is well known that, when light falls obliquely upon the external surface of a transparent medium, as on a plate of glass or a stratum of air, one portion is reflected and the other transmitted. But, when light falls very obliquely upon the internal surface, the whole is reflected, and not a ray is transmitted. In all cases the angles made by the incident and reflected rays with a perpendicular to the surface being equal, as the brightness of the reflected image depends on the quantity 157of light, those arising from total reflection must be by far the most vivid. The delusive appearance of water, so well known to African travellers and to the Arab of the desert as the Lake of the Gazelles, is ascribed to the reflection which takes place between strata of air of different densities, owing to radiation of heat from the arid sandy plains. The mirage described by Captain Mundy in his Journal of a Tour in India probably arises from this cause. “A deep precipitous valley below us, at the bottom of which I had seen one or two miserable villages in the morning, bore in the evening a complete resemblance to a beautiful lake; the vapour which played the part of water ascending nearly half way up the sides of the vale, and on its bright surface trees and rocks being distinctly reflected. I had not been long contemplating this phenomenon, before a sudden storm came on and dropped a curtain of clouds over the scene.”
An occurrence which happened on the 18th of November, 1804, was probably produced by reflection. Dr. Buchan, while watching the rising sun from the cliff about a mile to the east of Brighton, at the instant the solar disc emerged from the surface of the ocean, saw the cliff on which he was standing, a windmill, his own figure and that of a friend, depicted immediately opposite to him on the sea. This appearance lasted about ten minutes, till the sun had risen nearly his own diameter above the surface of the waves. The whole then seemed to be elevated into the air, and successively vanished. The rays of the sun fell upon the cliff at an incidence of 73° from the perpendicular, and the sea was covered with a dense fog many yards in height, which gradually receded before the rising sun. When extraordinary refraction takes place laterally, the strata of variable density are perpendicular to the horizon, and, if combined with vertical refraction, the objects are magnified as when seen through a telescope. From this cause, on the 26th of July, 1798, the cliffs of France, fifty miles off, were seen as distinctly from Hastings as if they had been close at hand; and even Dieppe was said to have been visible in the afternoon.
The stratum of air in the horizon is so much thicker and more dense than the stratum in the vertical, that the sun’s light is diminished 1300 times in passing through it, which enables us to look at him when setting without being dazzled. The loss of light, and consequently of heat, by the absorbing power of the 158atmosphere, increases with the obliquity of incidence. Of ten thousand rays falling on its surface, 8123 arrive at a given point of the earth if they fall perpendicularly; 7024 arrive if the angle of direction be fifty degrees; 2831, if it be seven degrees; and only five rays will arrive through a horizontal stratum. Since so great a quantity of light is lost in passing through the atmosphere, many celestial objects are altogether invisible from the plain, which may be seen from elevated situations. Diminished splendour, and the false estimate we make of distance from the number of intervening objects, lead us to suppose the sun and moon to be much larger when in the horizon than at any other altitude, though their apparent diameters are then somewhat less. Instead of the sudden transitions of light and darkness, the reflective power of the air adorns nature with the rosy and golden hues of the Aurora and twilight. Even when the sun is eighteen degrees below the horizon, a sufficient portion of light remains to show that at the height of thirty miles it is still dense enough to reflect light. The atmosphere scatters the sun’s rays, and gives all the beautiful tints and cheerfulness of day. It transmits the blue light in greatest abundance; the higher we ascend, the sky assumes a deeper hue; but, in the expanse of space, the sun and stars must appear like brilliant specks in profound blackness.
Constitution of Light according to Sir Isaac Newton—Absorption of Light—Colours of Bodies—Constitution of Light according to Sir David Brewster—New Colours—Fraunhofer’s Dark Lines—Dispersion of Light—The Achromatic Telescope—Homogeneous Light—Accidental and Complementary Colours—M. Plateau’s Experiments and Theory of Accidental Colours.
It is impossible thus to trace the path of a sunbeam through our atmosphere without feeling a desire to know its nature, by what power it traverses the immensity of space, and the various modifications it undergoes at the surfaces and in the interior of terrestrial substances.
Sir Isaac Newton proved the compound nature of white light, as emitted from the sun, by passing a sunbeam through a glass prism (N. 195), which, separating the rays by refraction, formed a spectrum or oblong image of the sun, consisting of seven colours, red, orange, yellow, green, blue, indigo, and violet—of which the red is the least refrangible, and the violet the most. But, when he reunited these seven rays by means of a lens, the compound beam became pure white as before. He insulated each coloured ray, and, finding that it was no longer capable of decomposition by refraction, concluded that white light consists of seven kinds of homogeneous light, and that to the same colour the same refrangibility ever belongs, and to the same refrangibility the same colour. Since the discovery of absorbent media, however, it appears that this is not the constitution of the solar spectrum.
We know of no substance that is either perfectly opaque or perfectly transparent. Even gold may be beaten so thin as to be pervious to light. On the contrary, the clearest crystal, the purest air or water, stops or absorbs its rays when transmitted, and gradually extinguishes them as they penetrate to greater depths. On this account objects cannot be seen at the bottom of very deep water, and many more stars are visible to the naked eye from the tops of mountains than from the valleys. The quantity of light that is incident on any transparent substance is 160always greater than the sum of the reflected and refracted rays. A small quantity is irregularly reflected in all directions by the imperfections of the polish by which we are enabled to see the surface; but a much greater portion is absorbed by the body. Bodies that reflect all the rays appear white, those that absorb them all seem black; but most substances, after decomposing the white light which falls upon them, reflect some colours and absorb the rest. A violet reflects the violet rays alone and absorbs the others. Scarlet cloth absorbs almost all the colours except red. Yellow cloth reflects the yellow rays most abundantly, and blue cloth those that are blue. Consequently colour is not a property of matter, but arises from the action of matter upon light. In fact, the law of action and reaction obtains in light as in every other department of nature, so that light cannot be reflected, refracted, much less absorbed, by any medium without being reacted upon by it. Thus a white riband reflects all the rays, but, when dyed red, the particles of the silk acquire the property of reflecting the red rays most abundantly and of absorbing the others. Upon this property of unequal absorption the colours of transparent media depend; for they also receive their colour from their power of stopping or absorbing some of the colours of white light, and transmitting others. As, for example, black and red inks, though equally homogeneous, absorb different kinds of rays; and, when exposed to the sun, they become heated in different degrees; while pure water seems to transmit all rays equally, and is not sensibly heated by the passing light of the sun. The rich dark light transmitted by a smalt-blue finger-glass is not a homogeneous colour like the blue or indigo of the spectrum, but is a mixture of all the colours of white light which the glass has not absorbed. The colours absorbed are such as mixed with the blue tint would form white light. When the spectrum of seven colours is viewed through a thin plate of this glass, they are all visible; and, when the plate is very thick, every colour is absorbed between the extreme red and the extreme violet, the interval being perfectly black; but, if the spectrum be viewed through a certain thickness of the glass intermediate between the two, it will be found that the middle of the red space, the whole of the orange, a great part of the green, a considerable part of the blue, a little of the indigo, and a very little of the violet, vanish, being absorbed by the blue glass; and that 161the yellow rays occupy a larger space, covering part of that formerly occupied by the orange on one side and by the green on the other: so that the blue glass absorbs the red light, which when mixed with the yellow constitutes orange; and also absorbs the blue light, which when mixed with the yellow forms the part of the green space next to the yellow. Hence, by absorption, green light is decomposed into yellow and blue, and orange light into yellow and red: consequently the orange and green rays, though incapable of decomposition by refraction, can be resolved by absorption, and actually consist of two different colours possessing the same degree of refrangibility. Difference of colour, therefore, is not a test of difference of refrangibility, and the conclusion deduced by Newton is no longer admissible as a general truth. By this analysis of the spectrum, not only with blue glass but with a variety of coloured media, Sir David Brewster, so justly celebrated for his optical discoveries, is of opinion that the solar spectrum consists of three primary colours, red, yellow, and blue, each of which exists throughout its whole extent, but with different degrees of intensity in different parts; and that the superposition of these three produces all the seven hues according as each primary colour is in excess or defect. That since a certain portion of red, yellow, and blue rays constitute white light, the colour of any point of the spectrum may be considered as consisting of the predominating colour at that point mixed with white light. Consequently, “by absorbing the excess of any colour at any point of the spectrum above what is necessary to form white light, such white light will appear at that point as never mortal eye looked upon before this experiment, since it possesses the remarkable property of remaining the same after any number of refractions, and of being capable of decomposition by absorption alone.” This analysis of light has been called in question by Professor Challis, of Cambridge, who does not admit of any resolution by absorbing media different from that by the prism, though he admits that a mixture of blue and yellow solar light produces green. Professor Stokes, on the contrary, does not allow that a mixture of blue and yellow solar light produces green, although that mixture produces green when the light is from other sources, for he found the gradation from sunlight to pass from yellow through diluted yellow, white, diluted blue to blue; so he does not admit of Sir David Brewster’s analysis of 162the spectrum; however, there appears to be still a doubt as to the real character of the phenomena presented by certain absorbing substances.
In addition to the seven colours of the Newtonian spectrum, Sir John Herschel has discovered a set of very dark red rays beyond the red extremity of the spectrum which can only be seen when the eye is defended from the glare of the other colours by a dark blue cobalt glass. He has also found that beyond the extreme violet there are visible rays of a lavender gray colour, which may be seen by throwing the spectrum on a sheet of paper moistened by the carbonate of soda. The illuminating power of the different rays of the spectrum varies with the colour. The most intense light is in the mean yellow ray, or, according to M. Fraunhofer, at the boundary of the orange and yellow.
When the prism is very perfect and the sunbeam small, so that the spectrum may be received on a sheet of white paper in its utmost state of purity, it presents the appearance of a riband shaded with all the prismatic colours, having its breadth irregularly striped or subdivided by an indefinite number of dark, and sometimes black lines. The greater number of these rayless lines are so extremely narrow that it is impossible to see them in ordinary circumstances. The best method is to receive the spectrum on the object-glass of a telescope, so as to magnify them sufficiently to render them visible. This experiment may also be made, but in an imperfect manner, by viewing a narrow slit between two nearly closed window-shutters through a very excellent glass prism held close to the eye, with its refracting angle parallel to the line of light. The rayless lines in the red portion of the spectrum become most visible as the sun approaches the horizon, while those in the blue extremity are most obvious in the middle of the day. When the spectrum is formed by the sun’s rays, either direct or indirect—as from the sky, clouds, rainbow, moon, or planets—the black bands are always found to be in the same parts of the spectrum, and under all circumstances to maintain the same relative positions. Similar dark lines are also seen in the light of the stars, in the electric light, and in the flame of combustible substances, though differently arranged, each star and each flame having a system of dark lines peculiar to itself. Dr. Wollaston and M. Fraunhofer, of Munich, discovered these lines deficient of rays independently of each other. 163M. Fraunhofer found that their number extends to nearly six hundred, but they are much more numerous. There are bright lines in the solar spectrum which also maintain a fixed position. Among the dark lines, M. Fraunhofer selected seven of the most remarkable, and determined their distances so accurately, that they now form standard and invariable points of reference for measuring the refractive powers of different media on the rays of light, which renders this department of optics as exact as any of the physical sciences. These lines are designated by the letters of the alphabet, beginning with B, which is in the red near the end of the spectrum; C is farther advanced in the red; D is in the orange; E in the green; F in the blue; G in the indigo; and H in the violet. By means of these fixed points, M. Fraunhofer has ascertained from prismatic observation the refrangibility of seven of the principal rays in each of ten different substances solid and liquid. The refraction increased in all from the red to the violet end of the spectrum. The rays that are wanting in the solar spectrum, which occasion the dark lines, were supposed to be absorbed by the atmosphere of the sun. But the annular eclipse which happened on the 15th of May, 1836, afforded Professor Forbes the means of proving that the dark lines in question cannot be attributed to the absorption of the solar atmosphere; they were neither broader nor more numerous in the spectrum formed during that phenomenon than at any other time, though the rays came only from the circumference of the sun’s disc, and consequently had to traverse a greater depth of his atmosphere.
Sir David Brewster found that in certain states of the atmosphere the obscure lines become much broader, and some of them deeply black; and he observed also, that, at the time the sun was setting in a veil of red light, part of the luminous spectrum was absorbed, whence he concluded that the earth’s atmosphere had absorbed the rays of light which occupied the dark bands. By direct experiments also the atmosphere was observed to act powerfully upon the rayless lines.
When a lens is used along with a prism, longitudinal dark lines of different breadths are seen to cross the bands, already described, at right angles; these M. Ragona-Scina and M. Babinet believe to be lines of interference which exist in light that has passed through a convex lens.
The lines are different both in kind and number in the spectra 164of gases and flames. In a highly-magnified spectrum from light passed through nitrous acid gas, Sir David Brewster counted 2000 dark bands. In the spectrum of a lamp, and generally of all white flames, none of the defective lines are found; so all such flames contain rays which do not exist in the light of the sun or stars. Brilliant red lines appear in the spectrum produced by the combustion of nitre upon charcoal; and in all artificial flames dark and bright bands exist, sometimes corresponding in position with those in the solar spectrum, and sometimes not.
A sunbeam received on a screen, after passing through a small round hole in a window-shutter, appears like a round white spot; but when a prism is interposed, the beam no longer occupies the same space. It is separated into the prismatic colours, and spread over a line of considerable length, while its breadth remains the same with that of the white spot. The act of spreading or separation is called the dispersion of the coloured rays. Dispersion always takes place in the plane of refraction, and is greater as the angle of incidence is greater. It varies inversely as the length of a wave of light, and directly as its velocity: hence towards the blue end of the spectrum, where the undulations of the rays are least, the dispersion is greatest. Substances have very different dispersive powers; that is to say, the spectra formed by two equal prisms of different substances, under precisely the same circumstances, are of different lengths. Thus, if a prism of flint-glass and one of crown-glass of equal refracting angles be presented to two rays of white light at equal angles, it will be found that the space over which the coloured rays are dispersed by the flint-glass is much greater than the space occupied by that produced by the crown-glass: and as the quantity of dispersion depends upon the refracting angle of the prism, the angles of the two prisms may be made such that, when the prisms are placed close together with their edges turned opposite ways, they will exactly oppose each other’s action, and will refract the coloured rays equally, but in contrary directions, so that an exact compensation will be effected, and the light will be refracted without colour (N. 195). The achromatic telescope is constructed on this principle. It consists of a tube with an object-glass or lens at one end to bring the rays to a focus, and form an image of the distant object, and a magnifying-glass at 165the other end to view the image thus formed. Now it is found that the object-glass, instead of making the rays converge to one point, disperses them, and gives a confused and coloured image: but by constructing it of two lenses in contact, one of flint and the other of crown-glass of certain forms and proportions, the dispersion is counteracted, and a perfectly well-defined and colourless image of the object is formed (N. 196). It was thought to be impossible to produce refraction without colour, till Mr. Hall, a gentleman of Worcestershire, constructed a telescope on this principle in the year 1733; and twenty-five years afterwards the achromatic telescope was brought to perfection by Mr. Dollond, a celebrated optician in London.
By means of Mr. Fraunhofer’s determination of the refraction of the principal rays in substances, their dispersive powers may be found (N. 197).
A perfectly homogeneous colour is very rarely to be found; but the tints of all substances are most brilliant when viewed in light of their own colour. The red of a wafer is much more vivid in red than in white light; whereas, if placed in homogeneous yellow light, it can no longer appear red, because there is not a ray of red in the yellow light. Were it not that the wafer, like all other bodies, whether coloured or not, reflects white light at its outer surface, it would appear absolutely black when placed in yellow light.
After looking steadily for a short time at a coloured object, such as a red wafer, on turning the eyes to a white substance, a green image of the wafer appears, which is called the accidental colour of red. All tints have their accidental colours: thus the accidental colour of orange is blue; that of yellow is indigo; of green, reddish white; of blue, orange-red; of violet, yellow; and of white, black; and vice versâ. When the direct and accidental colours are of the same intensity, the accidental is then called the complementary colour, because any two colours are said to be complementary to one another which produce white when combined.
From experiments by M. Plateau of Brussels, it appears that two complementary colours from direct impression, which would produce white when combined, produce black, or extinguish one another, by their union, when accidental; and also that the combination of all the tints of the solar spectrum produces white 166light if they be from a direct impression on the eye, whereas blackness results from a union of the same tints if they be accidental; and in every case where the real colours produce white by their combination, the accidental colours of the same tints produce black. When the image of an object is impressed on the retina only for a few moments, the picture left is exactly of the same colour with the object, but in an extremely short time the picture is succeeded by the accidental image. M. Plateau attributes this phenomenon to a reaction of the retina after being excited by direct vision, so that the accidental impression is of an opposite nature to the corresponding direct impression. He conceives that when the eye is excited by being fixed for a time on a coloured object, and then withdrawn from the excitement, it endeavours to return to its state of repose; but in so doing, that it passes this point, and spontaneously assumes an opposite condition, like a spring which, bent in one direction, in returning to its state of rest bends as much the contrary way. The accidental image thus results from a particular modification of the organ of sight, in virtue of which it spontaneously gives us a new sensation after it has been excited by direct vision. If the prevailing impression be a very strong white light, its accidental image is not black, but a variety of colours in succession. According to M. Plateau, the retina offers a resistance to the action of light, which increases with the duration of this action; whence, after looking intently at an object for a long time, it appears to decrease in brilliancy. The imagination has a powerful influence on our optical impressions, and has been known to revive the images of highly luminous objects months, and even years, afterwards.
Interference of Light—Undulatory Theory of Light—Propagation of Light—Newton’s Rings—Measurement of the Length of the Waves of Light, and of the Frequency of the Vibrations of Ether for each Colour—Newton’s Scale of Colours—Diffraction of Light—Sir John Herschel’s Theory of the Absorption of Light—Refraction and Reflection of Light.
Newton and most of his immediate successors imagined light to be a material substance, emitted by all self-luminous bodies in extremely minute particles, moving in straight lines with prodigious velocity, which, by impinging upon the optic nerves, produce the sensation of light. Many of the observed phenomena have been explained by this theory; it is, however, totally inadequate to account for the following circumstances.
When two equal rays of red light, proceeding from two luminous points, fall upon a sheet of white paper in a dark room, they produce a red spot on it which will be twice as bright as either ray would produce singly, provided the difference in the lengths of the two beams, from the luminous points to the red spot on the paper, be exactly the 0·0000258th part of an inch. The same effect will take place if the difference in the lengths be twice, three times, four times, &c., that quantity. But if the difference in the lengths of the two rays be equal to one-half of the 0·0000258th part of an inch, or to its 11⁄2, 21⁄2, 31⁄2, &c., part, the one light will entirely extinguish the other, and will produce absolute darkness on the paper where the united beams fall. If the difference in the lengths of their paths be equal to the 11⁄4, 21⁄4, 31⁄4, &c., of the 0·0000258th part of an inch, the red spot arising from the combined beams will be of the same intensity which one alone would produce. If violet light be employed, the difference in the lengths of the two beams must be equal to the 0·0000157th part of an inch, in order to produce the same phenomena; and for the other colours, the difference must be intermediate between the 0·0000258th and the 0·0000157th part of an inch. 168Similar phenomena may be seen by viewing the flame of a candle through two very fine slits in a card extremely near to one another (N. 198); or by admitting the sun’s light into a dark room through a pin-hole about the fortieth of an inch in diameter, receiving the image on a sheet of white paper, and holding a slender wire in the light. Its shadow will be found to consist of a bright white bar or stripe in the middle, with a series of alternate black and brightly-coloured stripes on each side. The rays which bend round the wire in two streams are of equal lengths in the middle stripe; it is consequently doubly bright from their combined effect; but the rays which fall on the paper on each side of the bright stripe, being of such unequal lengths as to destroy one another, form black lines. On each side of these black lines the rays are again of such lengths as to combine to form bright stripes, and so on alternately till the light is too faint to be visible. When any homogeneous light is used, such as red, the alternations are only black and red; but on account of the heterogeneous nature of white light, the black lines alternate with vivid stripes or fringes of prismatic colours, arising from the superposition of systems of alternate black lines and lines of each homogeneous colour. That the alternation of black lines and coloured fringes actually does arise from the mixture of the two streams of light which flow round the wire, is proved by their vanishing the instant one of the streams is interrupted. It may therefore be concluded, as often as these stripes of light and darkness occur, that they are owing to the rays combining at certain intervals to produce a joint effect, and at others to extinguish one another. Now it is contrary to all our ideas of matter to suppose that two particles of it should annihilate one another under any circumstances whatever; while, on the contrary, two opposing motions may; and it is impossible not to be struck with the perfect similarity between the interferences of small undulations of air or of water and the preceding phenomena. The analogy is indeed so perfect, that philosophers of the highest authority concur in the belief that the celestial regions are filled with an extremely rare and highly elastic medium or ether, whose particles are capable of receiving the vibrations communicated to them by self-luminous bodies, and of transmitting them to the optic nerves, so as to produce the sensation of light. The acceleration in the mean motion of 169Encke’s comet, as well as of the comet discovered by M. Biela, renders the existence of such a medium certain. It is clear that, in this hypothesis, the alternate stripes of light and darkness are entirely the effect of the interference of the undulations; for, by actual measurement, the length of a wave of the mean red rays of the solar spectrum is equal to the 0·0000258th part of an inch; consequently, when the elevations of the waves combine, they produce double the intensity of light that each would do singly; and when half a wave combines with a whole—that is, when the hollow of one wave is filled up by the elevation of another—darkness is the result. At intermediate points between these extremes, the intensity of the light corresponds to intermediate differences in the lengths of the rays.
The theory of interferences is a particular case of the general mechanical law of the superposition of small motions; whence it appears that the disturbance of a particle of an elastic medium, produced by two co-existent undulations, is the sum of the disturbances which each undulation would produce separately; consequently, the particle will move in the diagonal of a parallelogram, whose sides are the two undulations. If, therefore, the two undulations agree in direction, or nearly so, the resulting motion will be very nearly equal to their sum, and in the same direction; if they nearly oppose one another, the resulting motion will be nearly equal to their difference; and, if the undulations be equal and opposite, the resultant will be zero, and the particle will remain at rest.
The preceding experiments, and the inferences deduced from them, which have led to the establishment of the doctrine of the undulations of light, are the most splendid memorials of our illustrious countryman Dr. Thomas Young, though Huygens was the first to originate the idea.
It is supposed that the particles of luminous bodies are in a state of perpetual agitation, and that they possess the property of exciting regular vibrations in the molecules of the ethereal medium, corresponding to the vibrations of their own molecules; and that, on account of its elastic nature, one particle of the ether when set in motion communicates its vibrations to those adjacent, which in succession transmit them to those farther off; so that the primitive impulse is transferred from particle to particle, and the undulating motion darts through ether like a wave 170in water; so that light is motion, and therefore subject to the laws of dynamics and mathematical analysis. Although the progressive motion of light is known by experience to be uniform and in a straight line, the vibrations of the particles are always at right angles to the direction of the ray. The propagation of light is like the spreading of waves in water; but, if one ray alone be considered, its motion may be conceived by supposing a rope of indefinite length stretched horizontally, one end of which is held in the hand. If it be agitated to and fro at regular intervals, with a motion perpendicular to its length, a series of similar and equal tremors or waves will be propagated along it; and if the regular impulses be given in a variety of planes, as up and down, from right to left, and also in oblique directions, the successive undulations will take place in every possible plane. An analogous motion in the ether, when communicated to the optic nerves, would produce the sensation of common light. It is evident that the waves which flow from end to end of the cord in a serpentine form are altogether different from the perpendicular vibratory motion of each particle of the rope, which never deviates far from a state of rest. So, in ether, each particle vibrates perpendicularly to the direction of the ray; but these vibrations are totally different from and independent of the undulations which are transmitted through it, in the same manner as the vibrations of each particular ear of corn are independent of the waves that rush from end to end of a harvest-field when agitated by the wind.
The intensity of light depends upon the amplitude or extent of the vibrations of the particles of ether, while its colour depends upon their frequency. The time of the vibration of a particle of ether is, by theory, as the length of a wave directly, and inversely as its velocity. Now, as the velocity of light is known to be 190,000 miles in a second, if the lengths of the waves of the different coloured rays could be measured, the number of vibrations in a second corresponding to each could be computed. That has been accomplished as follows:—All transparent substances of a certain thickness, with parallel surfaces, reflect and transmit white light; but, if they be extremely thin, both the reflected and transmitted light is coloured. The vivid hues on soap-bubbles, the iridescent colours produced by heat on polished steel and copper, the fringes of colour between the laminæ of 171Iceland spar and sulphate of lime, all consist of a succession of hues disposed in the same order, totally independent of the colour of the substance, and determined solely by its greater or less thickness—a circumstance which affords the means of ascertaining the length of the waves of each coloured ray, and the frequency of the vibrations of the particles producing them. If a plate of glass be laid upon a lens of almost imperceptible curvature, before an open window, when they are pressed together a black spot will be seen in the point of contact, surrounded by seven rings of vivid colours, all differing from one another (N. 199). In the first ring, estimated from the black spot, the colours succeed each other in the following order:—black, very faint blue, brilliant white, yellow, orange, and red. They are quite different in the other rings, and in the seventh the only colours are pale bluish green and very pale pink. That these rings are formed between the two surfaces in apparent contact may be proved by laying a prism on the lens instead of the plate of glass, and viewing the rings through the inclined side of it that is next to the eye, which arrangement prevents the light reflected from the upper surface mixing with that from the surfaces in contact, so that the intervals between the rings appear perfectly black—one of the strongest circumstances in favour of the undulatory theory; for, although the phenomena of the rings can be explained by either hypothesis, there is this material difference, that, according to the undulatory theory, the intervals between the rings ought to be absolutely black, which is confirmed by experiment; whereas, by the doctrine of emanation, they ought to be half illuminated, which is not found to be the case. M. Fresnel, whose opinion is of the first authority, thought this test conclusive. It may therefore be concluded that the rings arise entirely from the interference of the rays: the light reflected from each of the surfaces in apparent contact reaches the eye by paths of different lengths, and produces coloured and dark rings alternately, according as the reflected waves coincide or destroy one another. The breadths of the rings are unequal; they decrease in width, and the colours become more crowded, as they recede from the centre. Coloured rings are also produced by transmitting light through the same apparatus; but the colours are less vivid, and are complementary to those reflected, consequently the central spot is white.
172The size of the rings increases with the obliquity of the incident light, the same colour requiring a greater thickness or space between the glasses to produce it than when the light falls perpendicularly upon them. Now, if the apparatus be placed in homogeneous instead of white light, the rings will all be of the same colour with that of the light employed, that is to say, if the light be red, the rings will be red, divided by black intervals. The size of the rings varies with the colour of the light. They are largest in red, and decrease in magnitude with the succeeding prismatic colours, being smallest in violet light.
Since one of the glasses is plane and the other spherical, it is evident that from the point of contact the space between them gradually increases in thickness all round, so that a certain thickness of air corresponds to each colour, which in the undulatory system measures the length of the wave producing it (N. 200). By actual measurement Sir Isaac Newton found that the squares of the diameters of the brightest part of each ring are as the odd numbers, 1, 3, 5, 7, &c.; and that the squares of the diameters of the darkest parts are as the even numbers, 0, 2, 4, 6, &c. Consequently, the intervals between the glasses at these points are in the same proportion. If, then, the thickness of the air corresponding to any one colour could be found, its thickness for all the others would be known. Now, as Sir Isaac Newton knew the radius of curvature of the lens, and the actual breadth of the rings in parts of an inch, it was easy to compute that the thickness of air at the darkest part of the first ring is the 1⁄89000 part of an inch, whence all the others have been deduced. As these intervals determine the length of the waves on the undulatory hypothesis, it appears that the length of a wave of the extreme red of the solar spectrum is equal to the 0·0000266th part of an inch; that the length of a wave of the extreme violet is equal to the 0·0000167th part of an inch; and, as the time of a vibration of a particle of ether producing any particular colour is directly as the length of a wave of that colour, and inversely as the velocity of light, it follows that the molecules of ether producing the extreme red of the solar spectrum perform 458 millions of millions of vibrations in a second; and that those producing the extreme violet accomplish 727 millions of millions of vibrations in the same time. The lengths of the waves of the intermediate colours, and the number of their vibrations, being intermediate between these two, white light, 173which consists of all the colours, is consequently a mixture of waves of all lengths between the limits of the extreme red and violet. The determination of these minute portions of time and space, both of which have a real existence, being the actual results of measurement, do as much honour to the genius of Newton as that of the law of gravitation.
The number of advancing waves of light in an inch is known to be from 37,600 to 59,880, and the number of lateral vibrations is from 458 to 727 billions in a second, but the extent of these lateral vibrations of the particles of the ethereal medium is not known, though both their extent and velocity are probably very small compared with the length of the advancing waves and the velocity of propagation. Colour is identified with the number of vibrations; but whether reflection, refraction, absorption, &c., have any relations to the lateral vibrations, or whether they are dependent in part upon some physical action of the ethereal medium unknown and unsuspected, are points as yet undetermined. To ascertain these circumstances, Dr. Faraday instituted a series of the most refined experiments upon the relation of the minute particles of metals to the vibrations of light.
Gold acts powerfully on light, and possesses a real transparency, transmitting green rays when very thin; and being capable of extreme division by solvents without losing its metallic character, its particles transmit rays of various colours according to their size; those that transmit the rose-colour in Bohemian glass are of inconceivable minuteness. The progressive waves of the ether are so long compared with the dimensions of the molecules to which gold can be reduced, that it seemed probable to Dr. Faraday when the latter were placed in a sunbeam that some effective relation might be discovered between them and the smaller vibrations of the ethereal medium; in which case, if reflection, refraction, &c., depended upon such relations, there was reason to expect that these functions would change sensibly by the substitution of different sized particles of the gold for one another. At one time Dr. Faraday hoped he had changed one colour into another by means of gold, which would have been equivalent to a change in the number of vibrations; but although he has not yet confirmed that result, his researches are of the greatest interest.[9]
174The phenomenon of the coloured rings takes place in vacuo as well as in air, which proves that it is the distance between the lenses alone, and not the air, which produces the colours. However, if water or oil be put between them, the rings contract, but no other change ensues; and Newton found that the thickness of different media at which a given tint is seen is in the inverse ratio of their refractive indices, so that the thickness of laminæ which could not otherwise be measured may be known by their colour; and, as the position of the colours in the rings is invariable, they form a fixed standard of comparison, well known as Newton’s scale of colours; each tint being estimated according to the ring to which it belongs from the central spot inclusively. Not only the periodical colours which have been described, but the colours seen in thick plates of transparent substances, the variable hues of feathers, of insects’ wings, mother-of-pearl, and of striated substances, all depend upon the same principle. To these may be added the coloured fringes surrounding the shadows of all bodies held in an extremely small beam of light, and the coloured rings surrounding the small beam itself when received on a screen.
When a very slender sunbeam, passing through a small pin-hole into a dark room, is received on a white screen, or plate of ground-glass, at the distance of a little more than six feet, the spot of light on the screen is larger than the pin-hole: and, instead of being bounded by shadow, it is surrounded by a series of coloured rings separated by obscure intervals. The rings are more distinct in proportion to the smallness of the beam (N. 201). When the light is white there are seven rings, which dilate or contract with the distance of the screen from the hole. As the distance of the screen diminishes, the white central spot contracts to a point and vanishes; and, on approaching still nearer, the rings gradually close in upon it, so that the centre assumes successively the most intense and vivid hues. When the light is homogeneous—red, for example—the rings are alternately red and black, and more numerous; and their breadth varies with the colour, being broadest in red light and narrowest in violet. The tints of the coloured fringes from white light, and their obliteration after the seventh ring, arise from the superposition of the different sets of fringes of all the coloured rays. The shadows of objects are also bordered by coloured fringes when held in this 175slender beam of light. If the edge of a knife or hair, for example, be held in it, the rays, instead of proceeding in straight lines past its edge, are bent when quite close to it, and proceed from thence to the screen in curved lines called hyperbolas; so that the shadow of the object is enlarged, and, instead of being at once bounded by light, is surrounded or edged with coloured fringes alternating with black bands, which are more distinct the smaller the pin-hole (N. 202). The fringes are altogether independent of the form or density of the object, being the same when it is round or pointed, when of glass or platinum. When the rays which form the fringes arrive at the screen, they are of different lengths, in consequence of the curved path they follow after passing the edge of the object. The waves are therefore in different phases or states of vibration, and either conspire to form coloured fringes or destroy one another in the obscure intervals. The coloured fringes bordering the shadows of objects were first described by Grimaldi in 1665; but, besides these, he noticed that there are others within the shadows of slender bodies exposed to a small sunbeam, a phenomenon which has already been mentioned to have afforded Dr. Young the means of proving, beyond all controversy, that coloured rings are produced by the interference of light.
It may be concluded that material substances derive their colours from two different causes: some from the law of interference, such as iridescent metals, peacocks’ feathers, &c.; others from the unequal absorption of the rays of white light, such as vermilion, ultramarine, blue, or green cloth, flowers, and the greater number of coloured bodies. The latter phenomena have been considered extremely difficult to reconcile with the undulatory theory of light, and much discussion has arisen as to what becomes of the absorbed rays. But that embarrassing question has been ably answered by Sir John Herschel in a most profound paper on the Absorption of Light by coloured Media, and cannot be better given than in his own words. It must, however, be premised, that, as all transparent bodies are traversed by light, they are presumed to be permeable to the ether. He says,—“Now, as regards only the general fact of the obstruction and ultimate extinction of light in its passage through gross media, if we compare the corpuscular and undulatory theories, we shall find that the former appeals to our ignorance, the latter 176to our knowledge, for its explanation of the absorptive phenomena. In attempting to explain the extinction of light on the corpuscular doctrine, we have to account for the light so extinguished as a material body, which we must not suppose annihilated. It may, however, be transformed; and among the imponderable agents, heat, electricity, &c., it may be that we are to search for the light which has become thus comparatively stagnant. The heating power of the solar rays gives a primâ facie plausibility to the idea of the transformation of light into heat by absorption. But, when we come to examine the matter more nearly, we find it encumbered on all sides with difficulties. How is it, for instance, that the most luminous rays are not the most calorific, but that, on the contrary, the calorific energy accompanies, in its greatest intensity, rays which possess comparatively feeble illuminating powers? These and other questions of a similar nature may perhaps admit of answer in a more advanced state of our knowledge; but at present there is none obvious. It is not without reason, therefore, that the question, ‘What becomes of light?’ which appears to have been agitated among the photologists of the last century, has been regarded as one of considerable importance as well as obscurity by the corpuscular philosophers. On the other hand, the answer to this question, afforded by the undulatory theory of light, is simple and distinct. The question, ‘What becomes of light?’ merges in the more general one, ‘What becomes of motion?’ And the answer, on dynamical principles, is, that it continues for ever. No motion is, strictly speaking, annihilated; but it may be divided, and the divided parts made to oppose and in effect destroy one another. A body struck, however perfectly elastic, vibrates for a time, and then appears to sink into its original repose. But this apparent rest (even abstracting from the inquiry that part of the motion which may be conveyed away by the ambient air) is nothing else than a state of subdivided and mutually destroying motion, in which every molecule continues to be agitated by an indefinite multitude of internally reflected waves, propagated through it in every possible direction, from every point in its surface on which they successively impinge. The superposition of such waves will, it is easily seen, at length operate their mutual destruction, which will be the more complete the more irregular the figure of the body, and the greater 177the number of internal reflections.” Thus Sir John Herschel, by referring the absorption of light to the subdivision and mutual destruction of the vibrations of ether in the interior of bodies, brings another class of phenomena under the laws of the undulatory theory.
According to Mr. Rankin’s hypothesis of Molecular Vortices[10] the absorption of light and radiant heat consists in the transference of motion from the molecules to their atmospheres, and conversely the emission of light and radiant heat is the transmission of motion from the atmospheres to the molecules. The great velocity of light and heat is a natural consequence of this hypothesis, according to which the vibratory masses must be extremely small compared with the forces exerted by them.
The ethereal medium pervading space is supposed to penetrate all material substances, occupying the interstices between their molecules; but in the interior of refracting media it exists in a state of less elasticity compared with its density in vacuo; and, the more refractive the medium, the less the elasticity of the ether within it. Hence the waves of light are transmitted with less velocity in such media as glass and water than in the external ether. As soon as a ray of light reaches the surface of a diaphanous reflecting substance, for example a plate of glass, it communicates its undulations to the ether next in contact with the surface, which thus becomes a new centre of motion, and two hemispherical waves are propagated from each point of this surface; one of which proceeds forward into the interior of the glass, with a less velocity than the incident waves; and the other is transmitted back into the air, with a velocity equal to that with which it came (N. 203). Thus, when refracted, the light moves with a different velocity without and within the glass; when reflected, the ray comes and goes with the same velocity. The particles of ether without the glass, which communicate their motions to the particles of the dense and less elastic ether within it, are analogous to small elastic balls striking large ones; for some of the motion will be communicated to the large balls, and the small ones will be reflected. The first would cause the refracted wave, and the last the reflected. Conversely, when the light passes from glass to air, the action is similar to large balls striking small ones. The small balls 178receive a motion which would cause the refracted ray, and the part of the motion retained by the large ones would occasion the reflected wave; so that, when light passes through a plate of glass or of any other medium differing in density from the air, there is a reflection at both surfaces; but this difference exists between the two reflections, that one is caused by a vibration in the same direction with that of the incident ray, and the other by a vibration in the opposite direction.
A single wave of air or ether would not produce the sensation of sound or light. In order to excite vision, the vibrations of the molecules of ether must be regular, periodical, and very often repeated: and, as the ear continues to be agitated for a short time after the impulse by which alone a sound becomes continuous, so also the fibres of the retina, according to M. d’Arcet, continue to vibrate for about the eighth part of a second after the exciting cause has ceased. The interval of time during which the impression lasts is longer for the blue than for red or white light: it must not be less than 0ʺ·34. Every one must have observed, when a strong impression is made by a bright light, that an object remains visible for a short time after shutting the eyes, which is supposed to be in consequence of the continued vibrations of the fibres of the retina. Occasionally the retina becomes insensible to feebly illuminated objects when continuously presented. If the eye be turned aside for a moment, the object becomes again visible. It is probably on this account that the owl makes so peculiar a motion with its head when looking at objects in the twilight. It is quite possible that many vibrations may be excited in the ethereal medium incapable of producing undulations in the fibres of the human retina, which yet have a powerful effect on those of other animals or of insects. Such may receive luminous impressions of which we are totally unconscious, and at the same time they may be insensible to the light and colours which affect our eyes, their perceptions beginning where ours end.
Polarization of Light—Defined—Polarization by Refraction—Properties of the Tourmaline—Double Refraction—All doubly Refracted Light is Polarized—Properties of Iceland Spar—Tourmaline absorbs one of the two Refracted Rays—Undulations of Natural Light—Undulations of Polarized Light—The Optic Axes of Crystals—M. Fresnel’s Discoveries on the Rays passing along the Optic Axis—Polarization by Reflection.
In giving a sketch of the constitution of light, it is impossible to omit the extraordinary property of its polarization, “the phenomena of which,” Sir John Herschel says, “are so singular and various, that to one who has only studied the common branches of physical optics it is like entering into a new world, so splendid as to render it one of the most delightful branches of experimental inquiry, and so fertile in the views it lays open of the constitution of natural bodies, and the minuter mechanism of the universe, as to place it in the very first rank of the physico-mathematical sciences, which it maintains by the rigorous application of geometrical reasoning its nature admits and requires.”
Light is said to be polarized, which, by being once reflected or refracted, is rendered incapable of being again reflected or refracted at certain angles. In general, when a ray of light is reflected from a pane of plate-glass, or any other substance, it may be reflected a second time from another surface, and it will also pass freely through transparent bodies. But, if a ray of light be reflected from a pane of plate-glass at an angle of 57°, it is rendered totally incapable of reflection at the surface of another pane of glass in certain definite positions, but it will be completely reflected by the second pane in other positions. It likewise loses the property of penetrating transparent bodies in particular positions, whilst it is freely transmitted by them in others. Light, so modified as to be incapable of reflection and transmission in certain directions, is said to be polarized.
Light may be polarized by reflection from any polished surface, and the same property is also imparted by refraction. It is proposed to explain these methods of polarizing light, to give a short 180account of its most remarkable properties, and to endeavour to describe a few of the splendid phenomena it exhibits.
If a brown tourmaline, which is a mineral generally crystallized in the form of a long prism, be cut longitudinally, that is, parallel to the axis of the prism, into plates about the thirtieth of an inch in thickness, and the surfaces polished, luminous objects may be seen through them, as through plates of coloured glass. The axis of each plate is in its longitudinal section parallel to the axis of the prism whence it was cut (N. 204). If one of these plates be held perpendicularly between the eye and a candle, and turned slowly round in its own plane, no change will take place in the image of the candle. But if the plate be held in a fixed position, with its axis or longitudinal section vertical, when a second plate of tourmaline is interposed between it and the eye, parallel to the first, and turned slowly round in its own plane, a remarkable change will be found to have taken place in the nature of the light. For the image of the candle will vanish and appear alternately at every quarter revolution of the plate, varying through all degrees of brightness down to total or almost total evanescence, and then increasing again by the same degrees as it had before decreased. These changes depend upon the relative positions of the plates. When the longitudinal sections of the two plates are parallel, the brightness of the image is at its maximum; and, when the axes of the sections cross at right angles, the image of the candle vanishes. Thus the light, in passing through the first plate of tourmaline, has acquired a property totally different from the direct light of the candle. The direct light would have penetrated the second plate equally well in all directions, whereas the refracted ray will only pass through it in particular positions, and is altogether incapable of penetrating it in others. The refracted ray is polarized in its passage through the first tourmaline, and experience shows that it never loses that property, unless when acted upon by a new substance. Thus, one of the properties of polarized light is the incapability of passing through a plate of tourmaline perpendicular to it, in certain positions, and its ready transmission in other positions at right angles to the former.
Many other substances have the property of polarizing light. If a ray of light falls upon a transparent medium, which has the same temperature, density, and structure throughout every part, 181as fluids, gases, glass, &c., and a few regularly crystallized minerals, it is refracted into a single pencil of light by the laws of ordinary refraction, according to which the ray, passing through the refracting surface from the object to the eye, never quits a plane perpendicular to that surface. Almost all other bodies, such as the greater number of crystallized minerals, animal and vegetable substances, gums, resins, jellies, and all solid bodies having unequal tensions, whether from unequal temperature or pressure, possess the property of doubling the image or appearance of an object seen through them in certain directions; because a ray of natural light falling upon them is refracted into two pencils which move with different velocities, and are more or less separated, according to the nature of the body and the direction of the incident ray. Whenever a ray of natural light is thus divided into two pencils in its passage through a substance, both of the transmitted rays are polarized. Iceland spar, a carbonate of lime, which by its natural cleavage may be split into the form of a rhombohedron, possesses the property of double refraction in an eminent degree, as may be seen by pasting a piece of paper, with a large pin-hole in it, on the side of the spar farthest from the eye. The hole will appear double when held to the light (N. 205). One of these pencils is refracted according to the same law as in glass or water, never quitting the plane perpendicular to the refracting surface, and is therefore called the ordinary ray. But the other does quit the plane, being refracted according to a different and much more complicated law, and on that account is called the extraordinary ray. For the same reason one image is called the ordinary, and the other the extraordinary image. When the spar is turned round in the same plane, the extraordinary image of the hole revolves about the ordinary image, which remains fixed, both being equally bright. But if the spar be kept in one position, and viewed through a plate of tourmaline, it will be found that, as the tourmaline revolves, the images vary in their relative brightness—one increases in intensity till it arrives at a maximum, at the same time that the other diminishes till it vanishes, and so on alternately at each quarter revolution, proving both rays to be polarized. For in one position the tourmaline transmits the ordinary ray, and reflects the extraordinary; and, after revolving 90°, the extraordinary ray is transmitted, and the ordinary ray is 182reflected. Thus another property of polarized light is, that it cannot be divided into two equal pencils by double refraction, in positions of the doubly refracting bodies in which a ray of common light would be so divided.
Were tourmaline like other doubly refracting bodies, each of the transmitted rays would be double; but that mineral, when of a certain thickness, after separating the light into two polarized pencils, absorbs that which undergoes ordinary refraction, and consequently shows only one image of an object. On this account tourmaline is peculiarly fitted for analyzing polarized light, which shows nothing remarkable till viewed through it or something equivalent.
The pencils of light, on leaving a double refracting substance, are parallel; and it is clear, from the preceding experiments, that they are polarized in planes at right angles to each other (N. 206). But that will be better understood by considering the change produced in common light by the action of the polarizing body. It has been shown that the undulations of ether, which produce the sensation of common light, are performed in every possible plane, at right angles to the direction in which the ray is moving. But the case is very different after the ray has passed through a doubly refracting substance, like Iceland spar. The light then proceeds in two parallel pencils, whose undulations are still indeed transverse to the direction of the rays, but they are accomplished in planes at right angles to one another, analogous to two parallel stretched cords, one of which performs its undulations only in a horizontal plane, and the other in a vertical or upright plane (N. 206). Thus the polarizing action of Iceland spar and of all doubly refracting substances is to separate a ray of common light, whose waves or undulations are in every plane, into two parallel rays, whose waves or undulations lie in planes at right angles to each other. By a simple mechanical law each vibratory motion of the first is resolved into two vibratory motions at right angles to one another. The ray of common light may be assimilated to a round rod, whereas the two polarized rays are like two parallel long flat rulers, one of which is laid horizontally on its broad surface, and the other horizontally on its edge. The alternate transmission and obstruction of one of these flattened beams by the tourmaline is similar to the facility with which a card may be passed between the bars of a 183grating or wires of a cage, if presented edgeways, and the impossibility of its passing in a transverse direction.
Although it generally happens that a ray of light, in passing through Iceland spar, is separated into two polarized rays, yet there is one direction along which it is refracted in one ray only, and that according to the ordinary law. This direction is called the optic axis (N. 207). Many crystals and other substances have two optic axes, inclined to each other, along which a ray of light is transmitted in one pencil by the law of ordinary refraction. The extraordinary ray is sometimes refracted towards the optic axis, as in quartz, zircon, ice, &c., which are therefore said to be positive crystals; but when it is bent from the optic axis, as in Iceland spar, tourmaline, emerald, beryl, &c., the crystals are negative, which is the most numerous class. The ordinary ray moves with uniform velocity within a doubly refracting substance, but the velocity of the extraordinary ray varies with the position of the ray relatively to the optic axis, being a maximum when its motion within the crystal is at right angles to the optic axis, and a minimum when parallel to it. Between these extremes its velocity varies according to a determinate law.
It had been inferred, from the action of Iceland spar on light, that in all doubly refracting substances one only of two rays is turned aside from the plane of ordinary refraction, while the other follows the ordinary law; and the great difficulty of observing the phenomena tended to confirm that opinion. M. Fresnel, however, proved by a most profound mathematical inquiry, à priori, that the extraordinary ray must be wanting in glass and other uncrystallized substances, and that it must necessarily exist in carbonate of lime, quartz, and other bodies having one optic axis, but that in a numerous class of substances, which possess two optic axes, both rays must undergo extraordinary refraction, and consequently that both must deviate from their original plane; and these results have been perfectly confirmed by subsequent experiments. This theory of refraction, which for generalization is perhaps only inferior to the law of gravitation, has enrolled the name of Fresnel among those which pass not away, and makes his early loss a subject of deep regret to all who take an interest in the higher paths of scientific research.
When a beam of common light is partly reflected at, and 184partly transmitted through a transparent surface, the reflected and refracted pencils contain equal quantities of polarized light, and their planes of polarization are at right angles to one another: hence, a pile of panes of glass will give a polarized beam by refraction. For, if a ray of common light pass through them, part of it will be polarized by the first plate, the second plate will polarize a part of what passes through it, and the rest will do the same in succession, till the whole beam is polarized, except what is lost by reflection at the different surfaces, or by absorption. This beam is polarized in a plane at right angles to the plane of reflection, that is, at right angles to the plane passing through the incident and reflected ray (N. 208).
By far the most convenient way of polarizing light is by reflection. A plane of plate-glass laid upon a piece of black cloth, on a table at an open window, will appear of a uniform brightness from the reflection of the sky or clouds. But if it be viewed through a plate of tourmaline, having its axis vertical, instead of being illuminated as before, it will be obscured by a large cloudy spot, having its centre quite dark, which will readily be found by elevating or depressing the eye, and will only be visible when the angle of incidence is 57°, that is, when the line from the eye to the centre of the black spot makes an angle of 33° with the surface of the reflector (N. 209). When the tourmaline is turned round in its own plane, the dark cloud will diminish, and entirely vanish when the axis of the tourmaline is horizontal, and then every part of the surface of the glass will be equally illuminated. As the tourmaline revolves, the cloudy spot will appear and vanish alternately at every quarter revolution. Thus, when a ray of light is incident on a pane of plate-glass at an angle of 57°, the reflected ray is rendered incapable of penetrating a plate of tourmaline whose axis is in the plane of incidence. Consequently it has acquired the same character as if it had been polarized by transmission through a plate of tourmaline, with its axis at right angles to the plane of reflection. It is found by experience that this polarized ray is incapable of a second reflection at certain angles and in certain positions of the incident plane. For if another pane of plate-glass, having one surface blackened, be so placed as to make an angle of 33° with the reflected ray, the image of the first pane will be reflected in its surface, and will be alternately illuminated 185and obscured at every quarter revolution of the blackened pane, according as the plane of reflection is parallel or perpendicular to the plane of polarization. Since this happens by whatever means the light has been polarized, it evinces another general property of polarized light, which is, that it is incapable of reflection in a plane at right angles to the plane of polarization.
All reflecting surfaces are capable of polarizing light, but the angle of incidence at which it is completely polarized is different in each substance (N. 210). It appears that the angle for plate-glass is 57°; in crown-glass it is 56° 55ʹ, and no ray will be completely polarized by water unless the angle of incidence be 53° 11ʹ. The angles at which different substances polarize light are determined by a very simple and elegant law, discovered by Sir David Brewster, “That the tangent of the polarizing angle for any medium is equal to the sine of the angle of incidence divided by the sine of the angle of refraction of that medium.” Whence also the refractive power even of an opaque body is known when its polarizing angle has been determined.
If a ray, polarized by refraction or by reflection from any substance not metallic, be viewed through a piece of Iceland spar, each image will alternately vanish and reappear at every quarter revolution of the spar, whether it revolves from right to left or from left to right; which shows that the properties of the polarized ray are symmetrical on each side of the plane of polarization.
Although there be only one angle in each substance at which light is completely polarized by one reflection, yet it may be polarized at any angle of incidence by a sufficient number of reflections. For, if a ray falls upon the upper surface of a pile of plates of glass at an angle greater or less than a polarizing angle, a part only of the reflected ray will be polarized, but a part of what is transmitted will be polarized by reflection at the surface of the second plate, part at the third, and so on till the whole is polarized. This is the best apparatus; but one plate of glass having its inferior surface blackened, or even a polished table, will answer the purpose.
Phenomena exhibited by the Passage of Polarized Light through Mica and Sulphate of Lime—The Coloured Images produced by Polarized Light passing through Crystals having one and two Optic Axes—Circular Polarization—Elliptical Polarization—Discoveries of MM. Biot, Fresnel, and Professor Airy—Coloured Images produced by the Interference of Polarized Rays—Fluorescence.
Such is the nature of polarized light and of the laws it follows. But it is hardly possible to convey an idea of the splendour of the phenomena it exhibits under circumstances which an attempt will now be made to describe.
If light polarized by reflection from a pane of glass be viewed through a plate of tourmaline, with its longitudinal section vertical, an obscure cloud, with its centre totally dark, will be seen on the glass. Now, let a plate of mica, uniformly about the thirtieth of an inch in thickness, be interposed between the tourmaline and the glass; the dark spot will instantly vanish, and, instead of it, a succession of the most gorgeous colours will appear, varying with every inclination of the mica, from the richest reds, to the most vivid greens, blues, and purples (N. 211). That they may be seen in perfection, the mica must revolve at right angles to its own plane. When the mica is turned round in a plane perpendicular to the polarized ray, it will be found that there are two lines in it where the colours entirely vanish. These are the optic axes of the mica, which is a doubly refracting substance, with two optic axes, along which light is refracted in one pencil.
No colours are visible in the mica, whatever its position may be with regard to the polarized light, without the aid of the tourmaline, which separates the transmitted ray into two pencils of coloured light complementary to one another, that is, which taken together would make white light. One of these it absorbs, and transmits the other; it is therefore called the analyzing plate. The truth of this will appear more readily if a film of sulphate of lime, between the twentieth and sixtieth of 187an inch thick, be used instead of the mica. When the film is of uniform thickness, only one colour will be seen when it is placed between the analyzing plate and the reflecting glass; as, for example, red. But, when the tourmaline revolves, the red will vanish by degrees till the film is colourless; then it will assume a green hue, which will increase and arrive at its maximum when the tourmaline has turned through ninety degrees; after that, the green will vanish and the red will reappear, alternating at each quadrant. Thus the tourmaline separates the light which has passed through the film into a red and a green pencil; in one position it absorbs the green and lets the red pass, and in another it absorbs the red and transmits the green. This is proved by analyzing the ray with Iceland spar instead of tourmaline; for, since the spar does not absorb the light, two images of the sulphate of lime will be seen, one red and the other green; and these exchange colours every quarter revolution of the spar, the red becoming green, and the green red; and, where the images overlap, the colour is white, proving the red and green to be complementary to each other. The tint depends on the thickness of the film. Films of sulphate of lime, the 0·00124 and 0·01818 of an inch respectively, give white light in whatever position they may be held, provided they be perpendicular to the polarized ray; but films of intermediate thickness will give all colours. Consequently, a wedge of sulphate of lime, varying in thickness between the 0·00124 and the 0·01818 of an inch, will appear to be striped with all colours when polarized light is transmitted through it. A change in the inclination of the film, whether of mica or sulphate of lime, is evidently equivalent to a variation in thickness.
When a plate of mica, held as close to the eye as possible, at such an inclination as to transmit the polarized ray along one of its optic axes, is viewed through the tourmaline with its axis vertical, a most splendid appearance is presented. The cloudy spot in the direction of the optic axis is seen surrounded by a set of vividly coloured rings of an oval form, divided into two unequal parts by a black curved band passing through the cloudy spot about which the rings are formed. The other optic axis of the mica exhibits a similar image (N. 212).
When the two optic axes of a crystal make a small angle with one another, as in nitre, the two sets of rings touch externally; 188and, if the plate of nitre be turned round in its own plane, the black transverse bands undergo a variety of changes, till, at last, the whole richly coloured image assumes the form of the figure 8, traversed by a black cross (N. 213). Substances with one optic axis have but one set of coloured circular rings, with a broad black cross passing through its centre, dividing the rings into four equal parts. When the analyzing plate revolves, this figure recurs at every quarter revolution; but in the intermediate positions it assumes the complementary colours, the black cross becoming white.
It is in vain to attempt to describe the beautiful phenomena exhibited by innumerable bodies which undergo periodic changes in form and colour when the analyzing plate revolves, but not one of them shows a trace of colour without the aid of tourmaline, or something equivalent, to analyze the light, and as it were to call these beautiful phantoms into existence. Tourmaline has the disadvantage of being itself a coloured substance; but that inconvenience may be obviated by employing a reflecting surface as an analyzing plate. When polarized light is reflected by a plate of glass at the polarizing angle, it will be separated into two coloured pencils; and, when the analyzing plate is turned round in its own plane, it will alternately reflect each ray at every quarter revolution, so that all the phenomena that have been described will be seen by reflection on its surface.
Coloured rings are produced by analyzing polarized light transmitted through glass melted and suddenly or unequally cooled; also through thin plates of glass bent with the hand, jelly indurated or compressed, &c. &c. In short, all the phenomena of coloured rings may be produced, either permanently or transiently, in a variety of substances, by heat and cold, rapid cooling, compression, dilatation, and induration; and so little apparatus is necessary for performing the experiments, that, as Sir John Herschel says, a piece of window glass or a polished table to polarize the light, a sheet of clear ice to produce the rings, and a broken fragment of plate-glass placed near the eye to analyze the light, are alone requisite to produce one of the most splendid of optical exhibitions.
Pressure produces remarkable changes in the optical properties of crystals. Compression, perpendicular to the axis, transforms a crystal with one optic axis into one with two. A slice of 189quartz and one of beryl, both cut perpendicularly to their axis, were compressed thus by MM. Moignot and Soleil. They found that the single system in the quartz, which is a positive crystal, was doubled in the direction of the compression, while in the beryl, which is a negative crystal, the duplication was perpendicular to the compression. In the quartz the axis of the double system coincided with the line of pressure, but in the tourmaline, which is a negative crystal, the line which joins the centres of the rings was perpendicular to the pressure.
If a positive crystal be compressed in the direction of its axis the tint of the rings descends, and that of a negative crystal rises. But if the crystals be dilated in the direction of their optic axis, the tints in positive crystals rise, and negative descend.
It has been observed, that when a ray of light, polarized by reflection from any surface not metallic, is analyzed by a doubly refracting substance, it exhibits properties which are symmetrical both to the right and left of the plane of reflection, and the ray is then said to be polarized according to that plane. This symmetry is not destroyed when the ray, before being analyzed, traverses the optic axis of a crystal having but one optic axis, as evidently appears from the circular forms of the coloured rings already described. Regularly crystallized quartz, however, forms an exception. In it, even though the rays should pass through the optic axis itself, where there is no double refraction, the primitive symmetry of the ray is destroyed, and the plane of primitive polarization deviates either to the right or left of the observer, by an angle proportional to the thickness of the plate of quartz. This angular motion, or true rotation of the plane of polarization, which is called circular polarization, is clearly proved by the phenomena. The coloured rings produced by all crystals having but one optic axis are circular, and traversed by a black cross concentric with the rings; so that the light entirely vanishes throughout the space enclosed by the interior ring, because there is neither double refraction nor polarization along the optic axis. But in the system of rings produced by a plate of quartz, whose surfaces are perpendicular to the axis of the crystal, the part within the interior ring, instead of being void of light, is occupied by a uniform tint of red, green, or blue, according to the thickness of the plate (N. 214). Suppose the 190plate of quartz to be 1⁄25 of an inch thick, which will give the red tint to the space within the interior ring; when the analyzing plate is turned, in its own plane through an angle of 171⁄2°, the red hue vanishes. If a plate of rock crystal 2⁄25 of an inch thick be used, the analyzing plate must revolve through 35° before the red tint vanishes, and so on, every additional 25th of an inch in thickness requiring an additional rotation of 171⁄2°; whence it is manifest that the plane of polarization revolves in the direction of a spiral within the rock crystal. It is remarkable that, in some crystals of quartz, the plane of polarization revolves from right to left, and in others from left to right, although the crystals themselves differ apparently only by a very slight, almost imperceptible, variety in form. In these phenomena the rotation to the right is accomplished according to the same laws, and with the same energy, as that to the left. But if two plates of quartz be interposed, which possess different affections, the second plate undoes, either wholly or partly, the rotatory motion which the first had produced, according as the plates are of equal or unequal thickness. When the plates are of unequal thickness, the deviation is in the direction of the strongest, and exactly the same with that which a third plate would produce equal in thickness to the difference of the two.
M. Biot has discovered the same properties in a variety of liquids. Oil of turpentine, and an essential oil of laurel, cause the plane of polarization to turn to the left, whereas the syrup of sugar-cane, and a solution of natural camphor, by alcohol, turn it to the right. A compensation is effected by the superposition or mixture of two liquids which possess these opposite properties, provided no chemical action takes place. A remarkable difference was also observed by M. Biot between the action of the particles of the same substances when in a liquid or solid state. The syrup of grapes, for example, turns the plane of polarization to the left as long as it remains liquid; but, as soon as it acquires the solid form of sugar, it causes the plane of polarization to revolve towards the right, a property which it retains even when again dissolved. Instances occur also in which these circumstances are reversed.
A ray of light passing through a liquid possessing the power of circular polarization is not affected by mixing other fluids with the liquid—such as water, ether, alcohol, &c.—which 191do not possess circular polarization themselves, the angle of deviation remaining exactly the same as before the mixture. Whence M. Biot infers that the action exercised by the liquids in question does not depend upon their mass, but that it is a molecular action exercised by the ultimate particles of matter, which depends solely upon the individual constitution, and is entirely independent of the positions and mutual distances of the particles with regard to each other. These important discoveries show that circular polarization surpasses the power of chemical analysis in giving certain and direct evidence of the similarity or difference existing in the molecular constitution of bodies, as well as of the permanency of that constitution, or of the fluctuations to which it may be liable. For example, no chemical difference has been discovered between syrup from the sugar-cane and syrup from grapes. Yet the first causes the plane of polarization to revolve to the right, and the other to the left; therefore some essential difference must exist in the nature of their ultimate molecules. The same difference is to be traced between the juices of such plants as give sugar similar to that from the cane, and those which give sugar like that obtained from grapes.
If chlorate of soda be dissolved in water, the liquid has no circular polarization; but if the solution be allowed to crystallize, some of the crystals turn the light to the right and others to the left. Now, if all those of one kind be gathered together and dissolved a second time, the liquid will have no circular polarization; but if crystals be allowed to form, some will turn the light to the right and others to the left, although only one kind was dissolved.[11]
It is a fact established by M. Biot, that in circular polarization the laws of rotation followed by the different simple rays of light are dissimilar in different substances. Whence he infers that the deviation of the simple rays from one another ought not to result from a special property of the luminous principle only, but that the proper action of the molecules must also concur in modifying the deviations of the simple rays differently in different substances.
One of the many brilliant discoveries of M. Fresnel is the production 192of circular and elliptical polarization by the internal reflection of light from plate-glass. He has shown that, if light polarized by any of the usual methods be twice reflected within a glass rhomb (N. 169) of a given form, the vibrations of the ether that are perpendicular to the plane of incidence will be retarded a quarter of a vibration, which causes the vibrating particles to describe circles, and the succession of such vibrating particles throughout the extent of a wave to form altogether a circular helix, or curve like a corkscrew. However, that only happens when the plane of polarization is inclined at an angle of 45° to the plane of incidence. When these two planes form an angle either greater or less, the succession of vibrating particles forms an elliptical helix, which curve may be represented by twisting a thread in a spiral about an oval rod. These curves will turn to the right or left, according to the position of the incident plane.
The motion of the ethereal medium in elliptical and circular polarization may be represented by the analogy of a stretched cord; for, if the extremity of such a cord be agitated at equal and regular intervals by a vibratory motion entirely confined to one plane, the cord will be thrown into an undulating curve lying wholly in that plane. If to this motion there be superadded another similar and equal, but perpendicular to the first, the cord will assume the form of an elliptical helix; its extremity will describe an ellipse, and every molecule throughout its length will successively do the same. But, if the second system of vibrations commence exactly a quarter of an undulation later than the first, the cord will take the form of a circular helix or corkscrew, the extremity will move uniformly in a circle, and every molecule throughout the cord will do the same in succession. It appears, therefore, that both circular and elliptical polarization may be produced by the composition of the motions of two rays in which the particles of ether vibrate in planes at right angles to one another.
Professor Airy, in a very profound and able paper published in the Cambridge Transactions, has proved that all the different kinds of polarized light are obtained from rock crystal. When polarized light is transmitted through the axis of a crystal of quartz, in the emergent ray the particles of ether move in a circular helix; and when it is transmitted obliquely so as to 193form an angle with the axis of the prism, the particles of ether move in an elliptical helix, the ellipticity increasing with the obliquity of the incident ray; so that, when the incident ray falls perpendicularly to the axis, the particles of ether move in a straight line. Thus quartz exhibits every variety of elliptical polarization, even including the extreme cases where the excentricity is zero, or equal to the greater axis of the ellipse (N. 215). In many crystals the two rays are so little separated, that it is only from the nature of the transmitted light that they are known to have the property of double refraction. M. Fresnel discovered, by experiments on the properties of light passing through the axis of quartz, that it consists of two superposed rays, moving with different velocities; and Professor Airy has shown that in these two rays the molecules of ether vibrate in similar ellipses at right angles to each other, but in different directions; that their ellipticity varies with the angle which the incident ray makes with the axis; and that, by the composition of their motions, they produce all the phenomena of polarized light observed in quartz.
It appears, from what has been said, that the molecules of ether always perform their vibrations at right angles to the direction of the ray, but very differently in the various kinds of light. In natural light the vibrations are rectilinear, and in every plane. In ordinary polarized light they are rectilinear, but confined to one plane; in circular polarization the vibrations are circular; and in elliptical polarization the molecules vibrate in ellipses. These vibrations are communicated from molecule to molecule, in straight lines when they are rectilinear, in a circular helix when they are circular, and in an oval or elliptical helix when elliptical.
Some fluids possess the property of circular polarization naturally, as oil of turpentine, the essential oils of laurel and lemon, sugar of grapes, and various liquids.
Elliptical polarization is produced by reflection from metallic surfaces. Mr. Baden Powell discovered it also in the light reflected from China ink, chromate of lead, plumbago, &c. Mr. Airy observed that the light reflected from the diamond is elliptically polarized; and Mr. Jamin has shown that this kind of polarization is generally produced by reflection from almost all transparent bodies, whatever their refractive power may be, 194especially from glass at angles very little different from the law of the tangents.
Water polarizes light circularly when between the points of maximum density and solidification; hence it becomes crystalline.
The coloured images from polarized light arise from the interference of the rays (N. 216). MM. Fresnel and Arago found that two rays of polarized light interfere and produce coloured fringes if they be polarized in the same plane, but that they do not interfere when polarized in different planes. In all intermediate positions, fringes of intermediate brightness are produced. The analogy of a stretched cord will show how this happens. Suppose the cord to be moved backwards and forwards horizontally at equal intervals; it will be thrown into an undulating curve lying all in one plane. If to this motion there be superadded another similar and equal, commencing exactly half an undulation later than the first, it is evident that the direct motion every molecule will assume, in consequence of the first system of waves, will at every instant be exactly neutralized by the retrograde motion it would take in virtue of the second; and the cord itself will be quiescent in consequence of the interference. But, if the second system of waves be in a plane perpendicular to the first, the effect would only be to twist the rope, so that no interference would take place. Rays polarized at right angles to each other may subsequently be brought into the same plane without acquiring the property of producing coloured fringes; but, if they belong to a pencil the whole of which was originally polarized in the same plane, they will interfere.
The manner in which the coloured images are formed may be conceived by considering that, when polarized light passes through the optic axis of a doubly refracting substance,—as mica, for example,—it is divided into two pencils by the analyzing tourmaline; and, as one ray is absorbed, there can be no interference. But, when polarized light passes through the mica in any other direction, it is separated into two white rays, and these are again divided into four pencils by the tourmaline, which absorbs two of them; and the other two, being transmitted in the same plane with different velocities, interfere and produce the coloured phenomena. If the analysis be made with Iceland spar, the single ray passing through the optic axis of the mica will be refracted into two rays, polarized in different planes, 195and no interference will happen. But, when two rays are transmitted by the mica, they will be separated into four by the spar, two of which will interfere to form one image, and the other two, by their interference, will produce the complementary colours of the other image when the spar has revolved through 90°; because, in such positions of the spar as produce the coloured images, only two rays are visible at a time, the other two being reflected. When the analysis is accomplished by reflection, if two rays are transmitted by the mica, they are polarized in planes at right angles to each other. And, if the plane of reflection of either of these rays be at right angles to the plane of polarization, only one of them will be reflected, and therefore no interference can take place; but in all other positions of the analyzing plate both rays will be reflected in the same plane, and consequently will produce coloured rings by their interference.
It is evident that a great deal of the light we see must be polarized, since most bodies which have the power of reflecting or refracting light also have the power of polarizing it. The blue light of the sky is completely polarized at an angle of 74° from the sun in a plane passing through his centre.
A constellation of talent almost unrivalled at any period in the history of science has contributed to the theory of polarization, though the original discovery of that property of light was accidental, and arose from an occurrence which, like thousands of others, would have passed unnoticed had it not happened to one of those rare minds capable of drawing the most important inferences from circumstances apparently trifling. In 1808, while M. Malus was accidentally viewing with a doubly-refracting prism a brilliant sunset reflected from the windows of the Luxembourg Palace in Paris, on turning the prism slowly round, he was surprised to see a very great difference in the intensity of the two images, the most refracted alternately changing from brightness to obscurity at each quadrant of revolution. A phenomenon so unlooked for induced him to investigate its cause, whence sprung one of the most elegant and refined branches of physical optics.
Fluorescence, or the internal dispersion of light, though far from possessing the beauty or extensive consequences of polarized light, is scarcely less wonderful. A variety of substances, such as canary-glass, a solution of sulphate of quinine, fluor-spar, and 196a great number of organic substances, have the property of diminishing the refrangibility of light by internal dispersion, consequently of increasing the length of the waves, and lowering the colour in the prismatic scale; it is therefore called degraded light, or fluorescence, because first discovered in fluor-spar.
If a piece of glass coloured by cobalt be fixed in a hole in a window-shutter of a dark room, a slab of white porcelain placed near it will appear blue; but if the slab be viewed through a yellow glass coloured by silver, it will appear to be almost quite black, because the yellow glass absorbs all the rays transmitted by the blue glass. If, however, a piece of canary-glass be laid on the slab while it is dark, every part of the canary-glass will shine as if it were self-luminous, and with so bright a light that anything written on the slab that was invisible before may now be distinctly read. Such is the singular phenomenon of internal dispersion, degraded light, or fluorescence. The brightness is by no means due to phosphorescence, because the canary-glass only shines when under the influence of the active or blue rays, whereas phosphorescent bodies shine by their own light—the latter has independent, the former dependent, emission; it is possible, however, that a connexion may hereafter be traced between them.
It appears from the analytical investigation of this phenomenon that the vibrations of the fluorescent substance are analogous to those of a sonorous body, as a bell or musical cord, which give the fundamental note and its harmonics. Now since there is a reciprocal action between the molecules of matter and light, when the light of the sun is absorbed by a substance capable of fluorescence, it puts the whole of its molecules into vibrations the same as its own, analogous to the fundamental note, while at the same time a certain number of molecules take more rapid vibrations exactly like the harmonics. The latter form new centres of light throughout the substance, which impart their vibrations to the ethereal medium around, and constitute fluorescence or degraded light. For example, in the experiment that has been described, the blue light imparted its own vibrations to all the molecules of the canary-glass, and also more rapid vibrations to a certain number of them. All of the blue rays were excluded by the yellow glass held before the eye; but it was pervious to the rays emanating in more rapid vibrations 197from the smaller number of molecules, which thus became really new centres of light, different from the sun’s light, though owing to it; the one celestial, the other terrestrial; and the latter vibrations being more rapid than those of the blue light, their refrangibility was less, and therefore their colour lower in the prismatic scale. Mr. Power computed from his formulæ, that fluorescent light is produced by undulations which are a major or minor third below the pitch of the general vibration of the medium—that is to say, below the vibrations which the whole molecules of the body most readily assume.
Professor Stokes, of Cambridge, who made the preceding experiment, found that the chemical rays from a point in the solar spectrum produced, in a solution of the sulphate of quinine, light of a sky-blue colour, which emanates in all directions from the liquid, and that this blue fluorescent light contains, when analysed, all the rays of the spectrum; hence he inferred that the dispersive power or fluorescence had lowered the refrangibility of the chemical rays, so as to make them visible: and Sir David Brewster observes that the new spectrum, of all colours into which they were transformed, must possess the extraordinary property of being a luminous spectrum, either without chemical rays or full of them. The dispersion in the quinine solution is greatest near the surface, but the blue emanation proceeds from every part of the liquid; and Sir John Herschel, who discovered the fluorescent property in this liquid, and gave it the name of epipolic light, found that the remainder of the beam, when it issued from the solution, though not apparently different from the incident white light, is yet so much changed in passing through the liquid, that it is no longer capable of producing fluorescence, though still capable of common dispersion. The blue light from the solution of quinine, when examined, consisted of rays extending over a great part of the spectrum.
By passing a sunbeam through a bluish kind of fluor-spar, Sir David Brewster perceived that the blue colour is not superficial, as it appears to be, but that some veins in the interior of the crystal disperse blue light, others pink, and even white light; in short, he met with fluorescence in such a variety of substances, that he concludes it may prevail more or less in the greater number of solids and liquids.
198Professor Draper, of New York, proved that the result is the same whether the incident light be polarized or not, and that the dispersed or degraded light is never polarized, but that it emanates in all directions, as if the substance were self-luminous; he made experiments with light from all parts of the solar spectrum, and with various substances, and always found that the refrangibility of the incident ray was diminished by internal dispersion, and that the colour was changed to suit the new refrangibility. Professor Draper has also shown that the law of action and reaction prevails in all the phenomena of the sunbeam, as in every other department of nature; so that a beam cannot be reflected, refracted, much less absorbed, without producing some change upon the recipient medium; and Mr. Power proved analytically that the solar rays can exercise no action upon any medium through which they are transmitted, without being accompanied by a diminution of refraction. He says, “The new light emanating from the fluorescent media is just like any other light of the same prismatic composition. In its physical properties it retains no trace of its parentage; it is of terrestrial origin, and its colour depends simply on its new refrangibility, having nothing to do with that of the producing rays, nor to the circumstance of their belonging to the visible or invisible part of the spectrum.” These phenomena can only be explained by the undulatory theory of light.
Objections to the Undulatory Theory, from a difference in the Action of Sound and Light under the same circumstances, removed—The Dispersion of Light according to the Undulatory Theory—Arago’s final proof that the Undulatory Theory is the Law of Nature.
The numerous phenomena of periodical colours arising from the interference of light, which do not admit of satisfactory explanation on any other principle than the undulatory theory, are the strongest arguments in favour of that hypothesis; and even cases which at one time seemed unfavourable to that doctrine have proved upon investigation to proceed from it alone. Such is the erroneous objection which has been made, in consequence of a difference in the mode of action of light and sound, under the same circumstances, in one particular instance. When a ray of light from a luminous point, and a diverging sound, are both transmitted through a very small hole into a dark room, the light goes straight forward and illuminates a small spot on the opposite wall, leaving the rest in darkness; whereas the sound on entering diverges in all directions, and is heard in every part of the room. These phenomena, however, instead of being at variance with the undulatory theory, are direct consequences of it, arising from the very great difference between the magnitude of the undulations of sound and those of light. The undulations of light are incomparably less than the minute aperture, while those of sound are much greater. Therefore when light, diverging from a luminous point, enters the hole, the rays round its edges are oblique, and consequently of different lengths, while those in the centre are direct, and nearly or altogether of the same lengths. So that the small undulations between the centre and the edges are in different phases, that is, in different states of undulation. Therefore the greater number of them interfere, and by destroying one another produce darkness all around the edges of the aperture; whereas the central rays, having the same phases, combine, and produce a spot of bright light on a wall or screen directly opposite the hole. 200The waves of air producing sound, on the contrary, being very large compared with the hole, do not sensibly diverge in passing through it, and are therefore all so nearly of the same length, and consequently in the same phase or state of undulation, that none of them interfere sufficiently to destroy one another. Hence all the particles of air in the room are set into a state of vibration, so that the intensity of the sound is very nearly everywhere the same. Strong as the preceding cases may be, the following experiment, made by M. Arago, seems to be decisive in favour of the undulatory doctrine. Suppose a plano-convex lens of very great radius to be placed upon a plate of very highly polished metal. When a ray of polarized light falls upon this apparatus at a very great angle of incidence, Newton’s rings are seen at the point of contact. But as the polarizing angle of glass differs from that of metal, when the light falls on the lens at the polarizing angle of glass, the black spot and the system of rings vanish. For although light in abundance continues to be reflected from the surface of the metal, not a ray is reflected from the surface of the glass that is in contact with it, consequently no interference can take place; which proves beyond a doubt that Newton’s rings result from the interference of the light reflected from both the surfaces apparently in contact (N. 199).
Notwithstanding the successful adaptation of the undulatory system to phenomena, the dispersion of light for a long time offered a formidable objection to that theory, which has been removed by Professor Powell of Oxford.
A sunbeam falling on a prism, instead of being refracted to a single point of white light, is separated into its component colours, which are dispersed or scattered unequally over a considerable space, of which the portion occupied by the red rays is the least, and that over which the violet rays are dispersed is the greatest. Thus the rays of the coloured spectrum, whose waves are of different lengths, have different degrees of refrangibility, and consequently move with different velocities, either in the medium which conveys the light from the sun, or in the refracting medium, or in both; whereas rays of all colours come from the sun to the earth with the same velocity. If, indeed, the velocities of the various rays were different in space, the aberration of the fixed stars, which is inversely as the velocity, 201would be different for different colours, and every star would appear as a spectrum whose length would be parallel to the direction of the earth’s motion, which is not found to agree with observation. Besides, there is no such difference in the velocities of the long and short waves of air in the analogous case of sound, since notes of the lowest and highest pitch are heard in the order in which they are struck. In fact, when the sunbeam passes from air into the prism, its velocity is diminished; and, as its refraction, and consequently its dispersion, depend solely upon the diminished velocity of the transmission of its waves, they ought to be the same for waves of all lengths, unless a connexion exists between the length of a wave and the velocity with which it is propagated. Now, this connexion between the length of a wave of any colour, and its velocity or refrangibility in a given medium, has been deduced by Professor Powell from M. Cauchy’s investigations of the properties of light on a peculiar modification of the undulatory hypothesis. Hence the refrangibility of the various coloured rays, computed from this relation for any given medium, when compared with their refrangibility in the same medium determined by actual observation, will show whether the dispersion of light comes under the laws of that theory. But, in order to accomplish this, it is clear that the length of the waves should be found independently of refraction, and a very beautiful discovery of M. Fraunhofer furnishes the means of doing so.
That philosopher obtained a perfectly pure and complete coloured spectrum, with all its dark and bright lines, by the interference of light alone, from a sunbeam passing through a series of fine parallel wires covering the object glass of a telescope. In this spectrum, formed independently of prismatic refraction, the positions of the coloured rays depend only on the lengths of their waves, and M. Fraunhofer found that the intervals between them are precisely proportional to the differences of these lengths. He measured the lengths of the waves of the different colours at seven fixed points, determined by seven of the principal dark and bright lines. Professor Powell, availing himself of these measures, has made the requisite computations, and has found that the coincidence of theory with observation is perfect for ten substances whose refrangibility had been previously determined by the direct measurements of M. Fraunhofer, and for ten others 202whose refrangibility has more recently been ascertained by M. Rudberg. Thus, in the case of seven rays in each of twenty different substances, solid and fluid, the dispersion of light takes place according to the laws of the undulatory theory: and there can hardly be a doubt that dispersion in all other bodies will be found to follow the same law. It is, however, an express condition of the connexion between the velocity of light and the length of its undulations, that the intervals between the vibrating molecules of the ethereal fluid should bear a sensible relation to the length of an undulation. The coincidence of the computed with the observed refractions shows that this condition is fulfilled within the refracting media; but the aberration of the fixed stars leads to the inference that it does not hold in the ethereal regions, where the velocities of the rays of all colours are the same. Strong as all that precedes is in favour of the undulatory theory, the relative velocity of light in air and water is the final and decisive proof. By the Newtonian theory the velocity is greater in water than in air, by the undulatory theory it is less; hence if a comparison could be made it would decide which is the law of nature. The difficulty consisted in comparing the velocity of light passing through a small extent of water with the velocity of light in air, which is 10,000 times greater than the velocity of the earth in its orbit. This delicate and difficult experiment was made by means of an instrument invented by Professor Wheatstone for measuring the velocity of electricity. It consists of a small mirror which revolves in its own plane like a coin spinning on its edge. When it revolves very rapidly the reflected image of an object changes its place perceptibly in an inconceivably small fraction of a second. The mirrors used in the experiment were made to revolve more than 1000 times in a second, by which means the places of the two images—one from light passing through air, and the other from light passing through an equal length of water—were found to be such as to prove that the velocity of light in air and in water is as 4 to 3, while by the Newtonian theory it is as 3 to 4. By this final and decisive proof the undulatory theory may from henceforth be regarded as the law of nature. This experiment was accomplished by M. Fizeau and M. Léon-Faucault, at the suggestion of M. Arago, whose eyesight did not permit him to undertake it himself.
Chemical or Photographic Rays of Solar Spectrum—Scheele, Ritter, and Wollaston’s Discoveries—Wedgwood’s and Sir Humphry Davy’s Photographic Pictures—The Calotype—The Daguerreotype—The Chromatype—The Cyanotype—Collodion—Sir John Herschel’s Discoveries in the Chemical Spectrum—M. Becquerel’s Discoveries of Inactive Lines in ditto—Thermic Spectrum—Phosphoric Spectrum—Electrical Properties—Parathermic Rays—Moser and Hunt’s Experiments—General Structure and antagonist Properties of Solar Spectrum—Defracted Spectrum.
The Solar Spectrum exercises an energetic action on matter, producing the most wonderful and mysterious changes on the organised and unorganised creation.
All bodies are probably affected by light, but it acts with greatest energy on such as are of weak chemical affinity, imparting properties to them which they did not possess before. Collodion and metallic salts, especially those of silver, whose molecules are held together by an unstable equilibrium, are of all bodies the most susceptible of its influence; the effects, however, vary with the substances employed, and with the different rays of the solar spectrum, the chemical properties of which are by no means alike. As early as 1772 M. Scheele showed that the pure white colour of chloride of silver was rapidly darkened by the blue rays of the solar spectrum, while the red rays had no effect upon it: and in 1801 M. Ritter discovered that invisible rays beyond the violet extremity have the property of blackening argentine salts, that this property diminishes towards the less refrangible part of the spectrum, and that the red rays have an opposite quality, that of restoring the blackened salt of silver to its original purity; from which he inferred that the most refrangible extremity of the spectrum has an oxygenising power, and the other that of deoxygenating. Dr. Wollaston found that gum guaiacum acquires a green colour in the violet and blue rays, and resumes its original tint in the red. No attempt had been made to trace natural objects by means of light reflected from them, till Mr. Wedgwood, together with Sir Humphry 204Davy, took up the subject: they produced profiles and tracings of objects on surfaces prepared with nitrate and chloride of silver, but they did not succeed in rendering their pictures permanent. This difficulty was overcome in 1814 by M. Niepcé, who produced a permanent picture of surrounding objects by placing in the focus of a camera-obscura a metallic plate covered with a film of asphalt dissolved in oil of lavender.
Mr. Fox Talbot, without any knowledge of M. Niepcé’s experiments, had been engaged in the same pursuit, and must be regarded as an independent inventor of photography, one of the most beautiful arts of modern times: he was the first who succeeded in using paper chemically prepared for receiving impressions from natural objects; and he also discovered a method of fixing permanently the impressions—that is, of rendering the paper insensible to any further action of light. In the calotype, one of Mr. Talbot’s applications of the art, the photographic surface is prepared by washing smooth writing-paper, first with a solution of nitrate of silver, then with bromide of potassium, and again with nitrate of silver, drying it at a fire after each washing; the paper is thus rendered so sensitive to light that even the passage of a thin cloud is perceptible on it, consequently it must be prepared by candle-light. Portraits, buildings, insects, leaves of plants—in short, every object is accurately delineated in a few seconds; and in the focus of a camera-obscura the most minute objects are so exactly depicted that the microscope reveals new beauties.
Since the effect of the chemical agency of light is to destroy the affinity between the salt and the silver, Mr. Talbot found that, in order to render these impressions permanent on paper, it was only necessary to wash it with salt and water, or with a solution of iodide of potassium. For these liquids the liquid hyposulphites have been advantageously substituted, which are the most efficacious in dissolving and removing the unchanged salt, leaving the reduced silver on the paper. The calotype picture is negative, that is, the lights and shadows are the reverse of what they are in nature, and the right-hand side in nature is the left in the picture; but if it be placed with its face pressed against photographic paper, between a board and a plate of glass, and exposed to the sun a short time, a positive and direct picture, as it is in nature, is formed: engravings may be exactly copied 205by this simple process, and a direct picture may be produced at once by using photographic paper already made brown by exposure to light.
While Mr. Fox Talbot was engaged in these very elegant discoveries in England, M. Daguerre had brought to perfection and made public that admirable process by which he has compelled Nature permanently to engrave her own works; and thus the talents of France and England have been combined in bringing to perfection this useful art. Copper, plated with silver, was successfully employed by M. Daguerre for copying nature by the agency of light. The surface of the plate is converted into an iodide of silver, by placing it horizontally with its face downwards in a covered box, in the bottom of which there is a small quantity of iodine which evaporates spontaneously. In three or four minutes the surface acquires a yellow tint, and then, screening it carefully from light, it must be placed in the focus of a camera obscura, where an invisible image of external objects will be impressed on it in a few minutes. When taken out, the plate must be exposed in another box to the action of mercurial vapour, which attaches itself to those parts of the plate which had been exposed to light, but does not adhere to such parts as had been in shadow; and as the quantity of mercury over the other parts is in exact proportion to the degree of illumination, the shading of the picture is perfect. The image is fixed, first by removing the iodine from the plate by plunging it into hyposulphite of soda, and then washing it in distilled water; by this process the yellow colour is destroyed, and in order to render the mercury permanent, the plate must be exposed a few minutes to nitric vapour, then placed in nitric acid containing copper or silver in solution at a temperature of 611⁄4° of Fahrenheit for a short time, and lastly polished with chalk. This final part of the process is due to Dr. Berre, of Vienna.
Nothing can be more beautiful than the shading of these chiaroscuro pictures when objects are at rest, but the least motion destroys the effect; the method therefore is more applicable to buildings than landscape. Colour is wanting; but the researches of Sir John Herschel give reason to believe that even this will ultimately be attained.
The most perfect impressions of seaweeds, leaves of plants, 206feathers, &c., may be formed by bringing the object into close contact with a sheet of photographic paper, between a board and plate of glass; then exposing the whole to the sun for a short time, and afterwards fixing it by the process described. The colours of the pictures vary with the preparation of the paper, by which almost any tint may be produced.
In the chromatype, a peculiar photograph discovered by Mr. Hunt, chromate of copper is used, on which a dark brown negative image is first formed, but by the continued action of light it is changed to a positive yellow picture on a white ground; the farther effect of light is checked by washing the picture in pure water.
In cyanotypes, a class of photographs discovered by Sir John Herschel, in which cyanogen in its combinations with iron forms the ground, the pictures are Prussian blue and white. In the chrysotype of the same eminent philosopher, the image is first received on paper prepared with the ammonia-citrate of iron, and afterwards washed with a neutral solution of gold. It is fixed by water acidulated with sulphuric acid, and lastly by hydriodate of potash, from which a white and purple photograph results. It is vain to attempt to describe the various beautiful effects which Sir John Herschel obtained from chemical compounds, and from the juices of plants; the juice of the red poppy gives a positive bluish purple image, that of the ten-week stock a fine rose colour on a pale straw-coloured ground.
Pictures may be made by exposure to sunshine, on all compound substances having a weak chemical affinity; but the image is often invisible, as in the Daguerreotype, till brought out by washing in some chemical preparation. Water is frequently sufficient; indeed Sir John Herschel brought out dormant photographs by breathing on them, and some substances are insensible to the action of light till moistened, as for example, gum guaiacum. Argentine papers, however, are little subject to the influence of moisture. The power of the solar rays is augmented in certain cases by placing a plate of glass in close contact over the sensitive surface.
All these various experiments, though highly interesting, have now been superseded. It was found that paper did not always answer for photography, on account of imperfections in its structure; silver plates were too expensive; and glass was 207found to be unimpressable. Nevertheless, M. Niepcé de Victor obtained beautiful results upon glass coated with albumen mixed with sensitive substances, which suggested the medium by means of which the art has been brought to its present perfection, and that final step is due to Mr. Scott Archer. He coated a plate of glass thinly with collodion, that is, gun-cotton dissolved in ether and alcohol, which dries into a delicate transparent film of extreme adhesiveness, and of such intense sensibility that the action of light upon it is so instantaneous that it arrests a stormy sea or a fleeting cloud before they have time to change. Now landscapes in chiaroscuro are produced of great beauty, which by the slower methods were mere masses of deep shade and broad light. Architecture is even more perfectly obtained, but it fails to give a pleasing representation of the human countenance.
Chemical action always accompanies the sun’s light, but the analysis of the solar spectrum has partly disclosed the wonderful nature of the emanation. In the research, properties most important and unexpected have been discovered by Sir John Herschel, who imprints the stamp of genius on all he touches—his eloquent papers can alone convey an adequate idea of their value in opening a field of inquiry vast and untrodden. The following brief and imperfect account of his experiments is all that can be attempted here:—
A certain degree of chemical energy is distributed through every part of the solar spectrum, and also to a considerable extent through the dark spaces at each extremity. This distribution does not depend on the refrangibility of the rays alone, but also on the nature of the rays themselves, and on the physical properties of the analyzing medium on which the rays are received, whose changes indicate and measure their action. The length of the photographic image of the same solar spectrum varies with the physical qualities of the surface on which it is impressed. When the solar spectrum is received on paper prepared with bromide of silver, the chemical spectrum, as indicated merely by the length of the darkened part, includes within its limits the whole luminous spectrum, extending in one direction far beyond the extreme violet and lavender rays, and in the other down to the extremest red: with tartrate of silver the darkening occupies not only all the space under the 208most refrangible rays, but reaches much beyond the extreme red. On paper prepared with formobenzoate of silver the chemical spectrum is cut off at the orange rays, with phosphate of silver in the yellow, and with chloride of gold it terminates with the green, with carbonate of mercury it ends in the blue, and on paper prepared with the percyanide of gold, ammonia, and nitrate of silver, the darkening lies entirely beyond the visible spectrum at its most refrangible extremity, and is only half its length, whereas in some cases chemical action occupies a space more than twice the length of the luminous image.
The point of maximum energy of chemical action varies as much for different preparations as the scale of action. In the greater number of cases the point of deepest blackening lies about the lower edge of the indigo rays, though in no two cases is it exactly the same, and in many substances it is widely different. On paper prepared with the juice of the ten-week stock (Mathiola annua) there are two maxima, one in the mean yellow and a weaker in the violet; and on a preparation of tartrate of silver Sir John Herschel found three, one in the least refrangible blue, one in the indigo, and a third beyond the visible violet. The decrease in photographic energy is seldom perfectly alike on both sides of the maximum. Thus at the most refrangible end of the solar spectrum the greatest chemical power is exerted in most instances where there is least light and heat, and even in the space where both sensibly cease.
Not only the intensity but the kind of action is different in the different points of the solar spectrum, as evidently appears from the various colours that are frequently impressed on the same analyzing surface, each ray having a tendency to impart its own colour. Sir John Herschel obtained a coloured image of the solar spectrum on paper prepared according to Mr. Talbot’s principle, from a sunbeam refracted by a glass prism and then highly condensed by a lens. The photographic image was rapidly formed and very intense, and, when withdrawn from the spectrum and viewed in common daylight, it was found to be coloured with sombre but unequivocal tints imitating the prismatic colours, which varied gradually from red through green and blue to a purplish black. After washing the surface in water, the tints became more decided by being kept a few days in the dark—a phenomenon, Sir John observes, of constant 209occurrence, whatever be the preparation of the paper, provided colours are produced at all. He also obtained a coloured image on nitrate of silver, the part under the blue rays becoming a blue brown, while that under the violet had a pinkish shade, and sometimes green appeared at the point corresponding to the least refrangible blue. Mr. Hunt found on a paper prepared with fluoride of silver that a yellow line was impressed on the space occupied by the yellow rays, a green band on the space under the green rays, an intense blue throughout the space on which the blue and indigo rays fell, and under the violet rays a ruddy brown appeared; these colours remained clear and distinct after being kept two months.
Notwithstanding the great variety in the scale of action of the solar spectrum, the darkening or deoxydizing principle that prevails in the more refrangible part rarely surpasses or even attains the mean yellow ray which is the point of maximum illumination; it is generally cut off abruptly at that point which seems to form a limit between the opposing powers which prevail at the two ends of the spectrum. The bleaching or oxydizing effect of the red rays on blackened muriate of silver discovered by M. Ritter of Jena, and the restoration by the same rays of discoloured gum guaiacum to its original tint by Dr. Wollaston, have already been mentioned as giving the first indications of that difference in the mode of action of the chemical rays at the two ends of the visible spectrum, now placed beyond a doubt.
The action exerted by the less refrangible rays beyond and at the red extremity of the solar spectrum, in most instances, so far from blackening metallic salts, protects them from the action of the diffused daylight: but, if the prepared surface has already been blackened by exposure to the sun, they possess the remarkable property of bleaching it in some cases, and under other circumstances of changing the black surface into a fiery red.
Sir John Herschel, to whom we owe most of our knowledge of the properties of the chemical spectrum, prepared a sheet of paper by washing it with muriate of ammonia, and then with two coats of nitrate of silver; on this surface he obtained an impression of the solar spectrum exhibiting a range of colours very nearly corresponding with its natural hues. But a very remarkable phenomenon occurred at the end of least refrangibility; the red rays exerted a protecting influence which preserved 210the paper from the change which it would otherwise have undergone from the deoxydizing influence of the dispersed light which always surrounds the solar spectrum, and this maintained its whiteness. Sir John met with another instance on paper prepared with bromide of silver, on which the whole of the space occupied by the visible spectrum was darkened down to the very extremity of the red rays, but an oxydizing action commenced beyond the extreme red, which maintained the whiteness of the paper to a considerable distance beyond the last traceable limit of the visible rays, thus evincing decidedly the existence of some chemical power over a considerable space beyond the least refrangible end of the spectrum. Mr. Hunt also found that on the Daguerreotype plate a powerful protecting influence is exercised by the extreme red rays. In these cases the red and those dark rays beyond them exert an action of an opposite nature to that of the violet and lavender rays.
The least refrangible part of the solar spectrum possesses also, under certain circumstances, a bleaching property, by which the metallic salts are restored to their original whiteness after being blackened by exposure to common daylight, or to the most refrangible rays of the solar spectrum.
Paper prepared with iodide of silver, when washed over with ferrocyanite of potash, blackens rapidly when exposed to the solar spectrum. It begins in the violet rays and extends over all the space occupied by the dark chemical rays, and over the whole visible spectrum down to the extreme red rays. This image is coloured, the red rays giving a reddish tint and the blue a blueish. In a short time a bleaching process begins under the red rays, and extends upwards to the green, but the space occupied by the extreme red is maintained perfectly dark. Mr. Hunt found that a similar bleaching power is exerted by the red rays on paper prepared with protocyanide of potassium and gold with a wash of nitrate of silver.
The application of a moderately strong hydriodate of potash to darkened photographic paper renders it peculiarly susceptible of being whitened by further exposure to light. If paper prepared with bromide of silver be washed with ferrocyanate of potash while under the influence of the solar spectrum, it is immediately darkened throughout the part exposed to the visible rays down to the end of the red, some slight interference being 211perceptible about the region of the orange and yellow. After this a bleaching action begins over the part occupied by the red rays, which extends to the green. By longer exposure an oval spot begins again to darken about the centre of the bleached space; but, if the paper receive another wash of the hydriodate of potash, the bleaching action extends up from the green, over the region occupied by the most refrangible rays and considerably beyond them, thus inducing a negative action in the most refrangible part of the spectrum.
In certain circumstances the red rays, instead of restoring darkened photographic paper to its original whiteness, produce a deep red colour. When Sir John Herschel received the spectrum on paper somewhat discoloured by exposure to direct sunshine, instead of whiteness, a red border was formed extending from the space occupied by the orange, and nearly covering that on which the red fell. When, instead of exposing the paper in the first instance to direct sunshine, it was blackened by the violet rays of a prismatic spectrum, or by a sunbeam that had undergone the absorptive action of a solution of ammonia-sulphate of copper, the red rays of the condensed spectrum produced on it, not whiteness, but a full and fiery red, which occupied the whole space on which any of the visible red rays had fallen; and this red remained unchanged, however long the paper remained exposed to the least refrangible rays.
Sunlight transmitted through red glass produces the same effect as the red rays of the spectrum in the foregoing experiment. Sir John Herschel placed an engraving over a paper blackened by exposure to sunshine, covering the whole with a dark red-brown glass previously ascertained to absorb every ray beyond the orange: in this way a photographic copy was obtained in which the shades were black, as in the original engraving; but the lights, instead of being white, were of the red colour of venous blood, and no other colour could be obtained by exposure to light, however long. Sir John ascertained that every part of the spectrum impressed by the more refrangible rays is equally reddened, or nearly so, by the subsequent action of the less refrangible; thus the red rays have the very remarkable property of assimilating to their own colour the blackness already impressed on photographic paper.
That there is a deoxydating property in the more refrangible 212rays, and an oxydating action in the less refrangible part of the spectrum, is manifest from the blackening of one and the bleaching effect of the other; but the peculiar action of the red rays in the experiments mentioned shows that some other principle exists different from contrariety of action. These opposite qualities are balanced or neutralized in the region of the mean yellow ray. But, although this is the general character of the photographic spectrum, under certain circumstances even the red rays have a deoxydating power, while the blue and violet exert a contrary influence; but these are rare exceptions.
The photographic action of the two portions of the solar spectrum being so different, Sir John Herschel tried the effect of their united action by superposing the less refrangible part of the spectrum over the more refrangible portion by means of two prisms; and he thus discovered that two rays of different refrangibility, and therefore of different lengths of undulation, acting simultaneously, produce an effect which neither, acting separately, can do.
Some circumstances that occurred during the analysis of the chemical spectrum seem to indicate an absorptive action in the sun’s atmosphere. The spectral image impressed on paper prepared with nitrate of silver and Rochelle salt commenced at, or very little below, the mean yellow ray, of a delicate lead colour; and when the action was arrested, such was the character of the whole photographic spectrum. But, when the light of the solar spectrum was allowed to continue its action, there was observed to come on suddenly a new and much more intense impression of darkness, confined in length to the blue and violet rays; and, what is most remarkable, confined also in breadth to the middle of the sun’s image, so far at least as to leave a border of the lead-coloured spectrum traceable, not only round the clear and well-defined convexity of the dark interior spectrum at the less refrangible end, but also laterally along both its edges; and this border was the more easily traced, and less liable to be mistaken, from its striking contrast of colour with the interior spectrum, the former being lead gray, the latter an extremely rich deep velvety brown. The less refrangible end of this interior brown spectrum presented a sharply terminated and regularly elliptical contour, the more refrangible a less decided one. “It may seem too hazardous,” Sir John continues, “to look for the cause 213of this very singular phenomenon in a real difference between the chemical agencies of those rays which issue from the central portion of the sun’s disc, and those which, emanating from its borders, have undergone the absorptive action of a much greater depth of its atmosphere; and yet I confess myself somewhat at a loss what other cause to assign for it. It must suffice, however, to have thrown out the hint, remarking only, that I have other, and I am disposed to think decisive, evidence of the existence of an absorptive solar atmosphere extending beyond the luminous one.” M. Arago observed that the rays from the centre of the sun have a greater photographic power than those from the edges, and the photographic images of the sun, taken on glass by M. Niepcé, were blood-red, much deeper in the centre, and on one occasion the image was surrounded by an auriol. Several circumstances concur in showing that there are influences also concerned in the transmission of the photographic action which have not yet been explained, as, for example, the influence which the time of the day exercises on the rapidity with which photographic impressions are made, the sun being much less effective two hours after passing the meridian than two hours before. There is also reason to suspect that the effect in some way depends on the latitude, since a much longer time is required to obtain an image under the bright skies of the tropics than in England; and it is even probable that there is a difference in the sun’s light in high and low latitudes, because an image of the solar spectrum, obtained on a Daguerreotype plate in Virginia, by Dr. Draper, differed from a spectral image obtained by Mr. Hunt on a similar plate in England. The inactive spaces discovered in the photographic spectrum by M. E. Becquerel, similar to those in the luminous spectrum, and coinciding with them, is also a phenomenon of which no explanation has yet been given; possibly the chemical rays may be absorbed by the atmosphere with those of light. Although chemical action extends over the whole luminous spectrum, and much beyond it, in gradations of more or less intensity, it is found by careful investigation to be by no means continuous; numerous inactive lines cross it, coinciding with those in the luminous image as far as it extends; besides, a very great number exist in the portions that are obscure, and which overlap the visible part. There are three extraspectral lines beyond the red, and some strongly marked groups on the 214obscure part beyond the violet; but the whole number of those inactive lines, especially in the dark spaces, is so great that it is impossible to count them.
Notwithstanding this coincidence in the inactive lines of the two spectra, photographic energy is independent of both light and heat, since it exerts the most powerful influence in those rays where they are least, and also in spaces where neither sensibly exist; but the transmission of the sun’s light through coloured media makes that independence quite evident. Heat and light pass abundantly through yellow glass, or a solution of chromate of potash; but the greater part of the chemical rays are excluded, and chlorine gas diluted with common air, though highly pervious to the luminous and calorific principles, has the same effect. Sir John Herschel found that a slight degree of yellow London fog had a similar effect with that of pale yellow media: he also remarked that a weak solution of azolitmine in potash, which admits a great quantity of green light, excludes chemical action; and some years ago the author, while making experiments on the transmission of chemical rays, observed that green glass, coloured by oxide of copper about the 20th of an inch thick, excludes the photographic rays; and, as M. Melloni has shown that substance to be impervious to the most refrangible calorific rays, it has the property of excluding the whole of the most refrangible part of the solar spectrum, visible and invisible. Green mica, if not too thin, has also the same effect, whereas amethyst, deep blue, and violet-coloured glasses, though they transmit a very little light, allow the chemical rays to pass freely. Thus light and photographic energy may be regarded as distinct parts of the solar beam, and both being propagated by vibrations of the etherial medium they are merely motion. Excellent images have been obtained of the moon in its different phases by Professor Secchi, at Rome; candlelight is nearly deficient of the chemical rays. How far they may influence crystallization and other molecular arrangements is unknown, but their power is universal wherever the solar beam falls, although their effect only becomes evident in cases of unstable molecular equilibrium.
It is not by vision alone that a knowledge of the sun’s rays is acquired: touch proves that they have the power of raising the temperature of substances exposed to their action. Sir William Herschel discovered that rays which produce the sensation of heat 215exist in the solar spectrum independent of those of light; when he used a prism of flint glass, he found that the warm rays are most abundant in the dark space a little beyond the red extremity of the spectrum, that from thence they decrease towards the violet, beyond which they are insensible. It may be concluded therefore, that the calorific rays vary in refrangibility, and that those beyond the extreme red are less refrangible than any rays of light. Since Sir William Herschel’s time it has been discovered that the calorific spectrum exceeds the luminous one in length in the ratio of 42 to 25, but the most singular phenomenon is its want of continuity. Sir John Herschel blackened the under side of a sheet of very thin white paper by the smoke of a lamp, and, having exposed the white side to the solar spectrum, he drew a brush dipped in spirit of wine over it, by which the paper assumed a black hue when sufficiently saturated. The heat in the spectrum evaporated the spirit first on those parts of the paper where it fell with greatest intensity, thereby restoring their white colour, and he thus discovered that the heat increases uniformly and gradually throughout the luminous spectrum, and that it comes to a maximum and forms a spot at a considerable distance beyond the extreme red. It then decreases, but again increasing it forms a second maximum spot, after which it ceases altogether through a short space, but is again renewed and forms two more insulated spots, and even a fifth may be traced at a little distance from the latter. These circumstances are probably owing to the absorbing action of the atmospheres of the sun and earth. “The effect of the former,” says Sir John, “is beyond our control, unless we could carry our experiments to such a point of delicacy as to operate separately on rays emanating from the centre and borders of the sun’s disc; that of the earth’s, though it cannot be eliminated any more than in the case of the sun’s, may yet be varied to a considerable extent by experiments made at great elevations, under a vertical sun, and compared with others where the sun is more oblique, the situation lower, and the atmospheric pressure of a temporarily high amount. Should it be found that this cause is in reality concerned in the production of the spots, we should see reason to believe that a large portion of solar heat never reaches the earth’s surface, and that what is incident on the summits of lofty mountains differs not only in quantity but also in quality from what the plains receive.”
216A remarkable phosphorescent property was discovered by M. E. Becquerel in the solar spectrum. Two luminous bands separated by a dark one are excited by the solar spectrum on paper covered with a solution of gum arabic, and strewed with powdered sulphuret of calcium or Canton’s phosphorus. One of the luminous bands occupies the space under the least refrangible violet rays, and the other that beyond the lavender rays, so that the dark band lies under the extreme violet and lavender rays. When the action of the light is continued, the whole surface beyond the least refrangible violet shines, the luminous bands already mentioned brightest; but all the space from the least refrangible violet to the extreme red remains dark. If the surface, prepared either with the sulphuret of calcium or Bologna stone, be exposed to the sun’s light for a little time, it becomes luminous all over; but when, in this state, a solar spectrum is thrown upon it, the whole remains luminous except the part from the least refrangible violet to the extreme red, on which space the light is extinguished; and when the temperature of the surface is raised by a lamp, the bright parts become more luminous and the dark parts remain dark. Glass stained by the protoxide of copper, which transmits only the red and orange rays, has the same effect with the less refrangible part of the spectrum; hence there can be no doubt that the most refrangible and obscure rays of the spectrum excite phosphorescence, while all the less refrangible rays of light and heat extinguish it.
Paper prepared with the sulphuret of barium, when under the solar spectrum, shows only one space of maximum luminous intensity, and the destroying rays are the same as in the sulphuret of calcium. Thus the obscure rays beyond the extreme violet produce light, while the luminous rays extinguish it.
The phosphoric spectrum has inactive lines which coincide with those in the luminous and chemical spectra, at least as far as it extends; but in order to be seen the spectrum must be received for a few seconds upon the prepared surface through an aperture in a dark room, then the aperture must be closed, and the temperature of the surface raised two or three hundred degrees; the phosphorescent parts then shine brilliantly and the dark lines appear black. Since the parts of similar refrangibility in different spectra are traversed by the same dark lines, rays of the same refrangibility are probably absorbed at the same time by the different media through which they pass.
217It appears from the experiments of MM. Becquerel and Biot, that electrical disturbances produce these phosphorescent effects. There is thus a mysterious connexion between the most refrangible rays and electricity which the experiments of M. E. Becquerel confirm, showing that electricity is developed during chemical action by the violet rays, that it is feebly developed by the blue and indigo, but that none is excited by the less refrangible part of the spectrum.
A series of experiments by Sir John Herschel have disclosed a new set of obscure rays in the solar spectrum, which seem to bear the same relation to those of heat that the photographic or chemical rays bear to the luminous. They are situate in that part of the spectrum which is occupied by the less refrangible visible colours, and have been named by their discoverer Parathermic rays. It must be held in remembrance that the region of greatest heat in the solar spectrum lies in the dark space beyond the visible red. Now, Sir John Herschel found that in experiments with a solution of gum guaiacum in soda, which gives the paper a green colour, the green, yellow, orange, and red rays of the spectrum invariably discharged the colour, while no effect was produced by the extra-spectral rays of heat, which ought to have had the greatest effect had heat been the cause of the phenomenon. When an aqueous solution of chlorine was poured over a slip of paper prepared with gum guaiacum dissolved in soda, a colour varying from a deep somewhat greenish hue to a fine celestial blue was given to it; and, when the solar spectrum was thrown on the paper while moist, the colour was discharged from all the space under the less refrangible luminous rays, at the same time that the more distant thermic rays beyond the spectrum evaporated the moisture from the space on which they fell; so that the heat spots became apparent. But the spots disappeared as the paper dried, leaving the surface unchanged; while the photographic impression within the visible spectrum increased in intensity; the non-luminous thermic rays, though evidently active as to heat, were yet incapable of effecting that peculiar chemical change which other rays of much less heating power were all the time producing. Sir John having ascertained that an artificial heat from 180° to 280° of Fahrenheit changed the green tint of gum guaiacum to its original yellow hue when moist, but that it had no effect when dry, he therefore 218tried whether heat from a hot iron applied to the back of the paper used in the last-mentioned experiment while under the influence of the solar spectrum might not assist the action of the calorific rays; but, instead of doing so, it greatly accelerated the discoloration over the spaces occupied by the less refrangible rays, but had no effect on the extra-spectral region of maximum heat. Obscure terrestrial heat, therefore, is capable of assisting and being assisted in effecting this peculiar change by those rays of the spectrum, whether luminous or thermic, which occupy its red, yellow, and green regions; while, on the other hand, it receives no such assistance from the purely thermic rays beyond the spectrum acting under similar circumstances and in an equal state of condensation.
The conclusions drawn from these experiments are confirmed by that which follows: a photographic picture formed on paper prepared with a mixture of the solutions of ammonia-citrate of iron and ferro-sesquicyanite of potash in equal parts, then thrown into water and afterwards dried, will be blue and negative, that is to say, the lights and shadows will be the reverse of what they are in nature. If in this state the paper be washed with a solution of proto-nitrate of mercury, the picture will be discharged; but if it be well washed and dried, and a hot smoothing-iron passed over it, the picture instantly reappears, not blue, but brown; if kept some weeks in this state in perfect darkness between the leaves of a portfolio, it fades, and almost entirely vanishes, but a fresh application of heat restores it to its full original intensity. This curious change is not the effect of light, at least not of light alone. A certain temperature must be attained, and that suffices in total darkness; yet, on exposing to a very concentrated spectrum a slip of the paper used in the last experiment, after the uniform blue colour has been discharged and a white ground left, this whiteness is changed to brown over the whole region of the red and orange rays, but not beyond the luminous spectrum.
Sir John thence concludes:—1st. That it is the heat of these rays, not their light, which operates the change; 2ndly. That this heat possesses a peculiar chemical quality which is not possessed by the purely calorific rays outside of the visible spectrum, though far more intense; and, 3rdly. That the heat radiated from obscurely hot iron abounds especially in rays analogous to those of the region of the spectrum above indicated.
219Another instance of these singular transformations may be noticed. The pictures formed on cyanotype paper rendered more sensitive by the addition of corrosive sublimate are blue on a white ground and positive, that is, the lights and shadows are the same as in nature, but, by the application of heat, the colour is changed from blue to brown, from positive to negative; even by keeping in darkness the blue colour is restored, as well as the positive character. Sir John attributes this, as in the former instance, to certain rays, which, regarded as rays of heat or light, or of some influence sui generis accompanying the red and orange rays of the spectrum, are also copiously emitted by bodies heated short of redness. He thinks it probable that these invisible parathermic rays are the rays which radiate from molecule to molecule in the interior of bodies, that they determine the discharge of vegetable colours at the boiling temperature, and also the innumerable atomic transformations of organic bodies which take place at the temperature below redness, that they are distinct from those of pure heat, and that they are sufficiently identified by these characters to become legitimate objects of scientific discussion.
The calorific and parathermic rays appear to be intimately connected with the discoveries of Messrs. Draper and Moser. Daguerre has shown that the action of light on the iodide of silver renders it capable of condensing the vapour of mercury which adheres to the parts affected by it. Professor Moser of Königsberg has proved that the same effect is produced by the simple contact of bodies, and even by their very near juxtaposition, and that in total darkness as well as in light. This discovery he announced in the following words:—“If a surface has been touched in any particular parts by any body, it acquires the property of precipitating all vapours, and these adhere to it or combine chemically with it on these spots differently from what they do on the untouched parts.” If we write on a plate of glass or any smooth surface whatever with blotting-paper, a brush, or anything else, and then clean it, the characters always reappear if the plate or surface be breathed upon, and the same effect may be produced even on the surface of mercury; nor is absolute contact necessary. If a screen cut in a pattern be held over a polished metallic surface at a small distance, and the whole breathed on, after the vapour has evaporated so that no trace is left on the surface, the pattern comes out when it is breathed on again.
220Professor Moser proved that bodies exert a very decided influence upon each other, by placing coins, cut stones, pieces of horn, and other substances, for a short time on a warm metallic plate: when the substance was removed, no impression appeared on the plate till it was breathed upon or exposed to the vapour of mercury, and then these vapours adhered only to the parts where the substance had been placed, making distinct images, which in some cases were permanent after the vapour was removed. Similar impressions were obtained on glass and other substances even when the bodies were not in contact, and the results were the same whether the experiments were performed in light or in darkness.
Mr. Grove found, when plates of zinc and copper were closely approximated, but not in contact, and suddenly separated, that one was positively and the other negatively electric; whence he inferred that the intervening medium was either polarised, or that a radiation analogous, if not identical, with that which produces Moser’s images takes place from plate to plate.
Mr. Hunt has shown that many of these phenomena depend on difference of temperature, and that, in order to obtain good impressions, dissimilar metals must be used. For example, gold, silver, bronze, and copper coins were placed on a plate of copper too hot to be touched, and allowed to remain till the plate cooled: all the coins had made an impression, the distinctness and intensity of which were in the order of the metals named. When the plate was exposed to the vapour of mercury the result was the same, but, when the vapour was wiped off, the gold and silver coins only had left permanent images on the copper. These impressions are often minutely perfect, whether the coins are in actual contact with the plate or one-eighth of an inch above it. The mass of the metal has a material influence on the result; a large copper coin makes a better impression on a copper plate than a small silver coin. When coins of different metals are placed on the same plate they interfere with each other.
When, instead of being heated, the copper plate was cooled by a freezing mixture, and bad conductors of heat laid upon it, as wood, paper, glass, &c., the result was similar.
Mr. Hunt, observing that a black substance leaves a stronger impression on a metallic surface than a white, applied the property to the art of copying prints, woodcuts, writing, and 221printing, on copper amalgamated on one surface and highly polished, merely by placing the object to be copied smoothly on the metal, and pressing it into close contact by a plate of glass: after some hours the plate is subjected to the vapour of mercury, and afterwards to that of iodine, when a black and accurate impression of the object comes out on a grey ground. Effects similar to those attributed to heat may also be produced by electricity. Mr. Karsten, by placing a glass plate upon one of metal, and on the glass plate a medal subjected to discharges of electricity, found a perfect image of the medal impressed on the glass, which could be brought into evidence by either mercury or iodine; and, when several plates of glass were interposed between the medal and the metallic plate, each plate of glass received an image on its upper surface after the passage of electrical discharges. These discharges have the remarkable power of restoring impressions that have been long obliterated from plates by polishing—a proof that the disturbances upon which these phenomena depend are not confined to the surface of the metals, but that a very decided molecular change has taken place to a considerable depth. Mr. Hunt’s experiments prove that the electro-negative metals make the most decided images upon electro-negative plates, and vice versâ. M. Matteucci has shown that a discharge of electricity does not visibly affect a polished silver plate, but that it produces an alteration which renders it capable of condensing vapour.
The impression of an engraving was made by laying it face downwards on a silver plate iodized, and placing an amalgamated copper plate upon it; it was left in darkness fifteen hours, during which time an impression of the engraving had been made on the amalgamated plate through the paper.
An iodized silver plate was placed in darkness with a coil of string laid on it, and with a polished silver plate suspended one-eighth of an inch above it: after four hours they were exposed to the vapours of mercury, which became uniformly deposited on the iodized plate, but on the silver one there was a sharp image of the string, so that this image was formed in the dark, and even without contact. Coins or other objects leave their impressions in the same manner with perfect sharpness and accuracy, when brought out by vapour without contact, in darkness, and on simple metals.
222Red and orange coloured media, smoked glass, and all bodies that transmit or absorb the hot rays freely, leave strong impressions on a plate of copper, whether they be in contact or one-eighth of an inch above it. Heat must be concerned in this, for a solar spectrum concentrated by a lens was thrown on a polished plate of copper, and kept on the same spot by a heliostat for two or three hours: when exposed to mercurial vapour, a film of the vapour covered the plate where the diffused light which always accompanies the solar spectrum had fallen. On the obscure space occupied by the maximum heating power of Sir William Herschel, and also on the great heat spot in the thermic spectrum of Sir John Herschel, the condensation of the mercury was so thick that it stood out a distinct white spot on the plate, while over the whole space that had been under the visible spectrum the quantity of vapour was much less than that which covered the other parts, affording distinct evidence of a negative effect in the luminous spectrum and of the power of the hot rays, which is not always confined to the surface of the metal, since in many instances the impressions penetrated to a considerable depth below it, and consequently were permanent.
Several of these singular effects appear to be owing to the mutual action of molecules in contact while in a different state, whether of electricity or temperature: others clearly point at some unknown influence exerted between surfaces at a distance, and affecting their molecular structure: possibly it may be the parathermic rays, which have a peculiar chemical action even in total darkness. In the last experiment the effect is certainly produced by the positive portion of one of those remarkable antagonist principles which characterise the solar spectrum.
Thus it appears that the prism resolves the pure white sunbeam into three superposed spectra, each varying in refrangibility and intensity throughout its whole length; the visible part is overlapped at one end by the chemical or photographic rays, and at the other by the thermic, but the two latter so much exceed the visible part, that the linear dimensions of the three—the luminous, thermic, and photographic—are in proportion to the numbers 25, 42·10, and 55·10, so that the whole solar spectrum is twice as long as its visible part. The two extremities exert a decided antagonist energy. The least refrangible luminous rays obliterate the action of the photographic rays, while the latter 223produce phosphorescent light, which is extinguished by the least refrangible luminous rays. According to Mr. Hunt’s experiment, the hot rays condense mercurial vapour on a polished metallic plate, while the luminous rays prevent its formation. Electricity is excited by the chemical rays, while the parathermic are found in the less refrangible rays alone. Each of the spectra is crossed by coloured and rayless lines peculiar to itself, and these are traversed at right angles by innumerable dark lines of various breadths, the whole forming an inexpressibly wonderful and glorious creation.
The arrangement varies a little according to the material of the prism and the manner of producing the spectrum, as in that obtained by Professor Draper from diffracted light. It was formed by a beam diffracted by passing through a netting of fine wire, or by reflection from a polished surface of steel, having fine parallel lines drawn on it. This diffracted spectrum is divided into two equal parts in the centre of the yellow; and as in the prismatic spectrum, one half is antagonist to the other half, the red or negative end undoing what the positive or violet end has done. The centre of the yellow is the hottest part, and the heat decreases to both extremities. A line of cold is supposed to exist on this spectrum answering to Fraunhofer’s dark line H.
The undulations of the ethereal medium which constitute a sunbeam must be infinitely varied, each influence having a vibration peculiar to itself. Those of light are certainly transverse to the direction of the ray; while Professor Draper believes that those of heat are normal, that is, in the direction of the ray, like those of sound. A doubt exists whether the vibrations of polarised light are perpendicular to the plane of polarisation or in that plane. Professor Stokes of Cambridge has come to the conclusion, both from the diffracted spectrum and theory, that they are perpendicular to the plane of polarisation, but M. Holtzmann is of opinion that they are in that plane, so the subject is still open to discussion.
Size and Constitution of the Sun—The Solar Spots—Intensity of the Sun’s Light and Heat—The Sun’s Atmosphere—His influence on the Planets—Atmospheres of the Planets—The Moon has none—Lunar heat—The Differential Telescope—Temperature of Space—Internal Heat of the Earth—Zone of constant Temperature—Increase of Heat With the Depth—Central Heat—Volcanic Action—Quantity of Heat received from the Sun—Isogeothermal Lines—Line of perpetual Congelation—Climate—Isothermal Lines—Same quantity of Heat annually received and radiated by the Earth.
The sun is a globe 880,000 miles in diameter: what his body may be it is impossible to conjecture, but it seems to be a dark mass surrounded by an extensive atmosphere at a certain height in which there is a stratum of luminous clouds which constitutes the photosphere of the sun. Above it rises the true solar atmosphere, visible as an aureola or corona during annular and total eclipses, and probably the cause of the peculiar phenomena in the photographic image of the sun already mentioned. Through occasional openings in the photosphere or mottled ocean of flame, the dark nucleus appears like black spots, often of enormous size. These spots are almost always comprised within a zone of the sun’s surface, whose breadth measured on a solar meridian does not extend beyond 301⁄2° on each side of his equator, though they have been seen at a distance of 391⁄2°. The dark central part of the spots is surrounded by a succession of obscure cloudy envelopes increasing in brightness up to a penumbra, sometimes there are three or more shades, but it requires a good telescope to distinguish the intermediate ones. The spots gradually increase in size and number from year to year to a maximum, and then as gradually decrease to a minimum, accomplishing regular vicissitudes in periods of about eleven years, and are singularly connected with the cycles of terrestrial magnetism. From their extensive and rapid changes, there is every reason to believe that the exterior and incandescent part of the sun is gaseous.
Doubts have arisen as to the uniformity of the quantity of 225heat emitted by the sun. Sir William Herschel was the first to suspect that it was affected by the quantity and magnitude of the spots on his surface; Professor Secchi has observed that the spots are less hot than the luminous part; and now Professor Wolf has perceived that the amount of heat emitted by the sun varies periodically with the spots every 11·11 years, or nearly nine times in a century, beginning at the commencement of the present one. He has discovered a sub-period in that of the spots, which no doubt has an effect on the quantity of solar heat. So the unaccountable vicissitudes in the temperature of different years may ultimately be found to depend upon the constitution of the sun himself.
The intensity of the sun’s light diminishes from the centre to the circumference of the solar disc. His direct light has been estimated to be equal to that of 5563 wax candles of moderate size placed at the distance of one foot from an object; that of the moon is probably only equal to the light of one candle at the distance of 12 feet: consequently the light of the sun is more than three hundred thousand times greater than that of the moon. According to Professor Secchi’s experiments at Rome, the heat of the solar image is almost twice as great at the centre as at the edge. The maximum heat, however, is not in the centre, but in the solar equator, and the spots are less hot than the rest of the surface.
The oceans of light and heat probably arising from electric or chemical processes of immense energy that continually take place at the sun’s surface (N. 217) are transmitted in undulations by the ethereal medium in all directions; but notwithstanding the sun’s magnitude and the inconceivable intensity of light and heat that must exist at his surface, as the intensity of both diminishes as the square of the distance increases, his kindly influence can hardly be felt at the boundaries of our system. In Uranus the sun must be seen like a small brilliant star not above the hundred and fiftieth part as bright as he appears to us, but that is 2000 times brighter than our moon, so that he is really a sun to Uranus, and may impart some degree of warmth. But if we consider that water would not remain fluid in any part of Mars, even at his equator, and that, in the temperate zones of the same planet, even alcohol and quicksilver would freeze, we may form some idea of the cold that must reign in Uranus and Neptune. 226The climate of Venus more nearly resembles that of the earth, though, excepting at her poles, much too hot for animal and vegetable life such as they exist here, for she receives seven times as much light and heat as the earth does; but in Mercury the mean heat from the intensity of the sun’s rays must be above that of boiling quicksilver, and water would boil even at his poles. Thus the planets, though kindred with the earth in motion and form, are, according to our experience, totally unfit for the habitation of such a being as man, unless indeed their temperature should be modified by circumstances of which we are not aware, and which may increase or diminish the sensible heat so as to render them habitable. In our utter ignorance it may be observed, that the earth, if visible at all from Neptune, can only be a minute telescopic object; that from the nearest fixed star the sun must dwindle to a mere point of light; that the whole solar system would there be hid by a spider’s thread; and that the starry firmament itself is only the first series of starry systems, the numbers of which are bounded alone by the imperfection of our space-penetrating instruments. In this overwhelming majesty of creation, it seems rash to affirm that the earth alone is inhabited by intelligent beings, and thus to limit the Omnipotent, who has made nothing in vain.
Several of the planets have extensive and dense atmospheres: according to Schroëter the atmosphere of Ceres is more than 668 miles high, and that of Pallas has an elevation of 465 miles, but not a trace of an atmosphere can be perceived round Vesta. The attraction of the earth has probably deprived the moon of hers, for the refractive power of the air at the surface of the earth is at least a thousand times as great as at the surface of the moon: the lunar atmosphere must therefore be of a greater degree of rarity than can be produced by our best air-pumps. This is confirmed by Arago’s observations during a solar eclipse, when no trace of a lunar atmosphere could be seen. Since then, however, some indications of air have been perceived in the lunar valleys. In taking photographic images of the moon and Jupiter at Rome, Professor Secchi found that the light of the full moon is to that of the quarter moon as 3 to 1. Jupiter gives a photographic image as bright and vigorous as the brightest part of the moon; but although the light of Jupiter is less than that of the moon, he is nearly five times farther from the sun; and as light 227diminishes as the square of the distance increases, the light of Jupiter is proportionally greater than that of the moon, consequently Jupiter’s atmosphere reflects more light than the dark volcanic soil of the moon; thus Professor Secchi observes photography may in time reveal the quality of the materials of which the celestial bodies are formed.
The effect of the earth’s atmosphere on lunar heat is remarkable. Professor Forbes proved that the direct light of the full moon is incapable of raising a thermometer the one three thousandth part of a Centigrade degree, at least in England; but at an elevation of 8870 feet on the Peak of Teneriffe, Mr. Piazzi Smyth found a very sensible heat from the moon, although she was then 19° south of the equator; so it is no doubt absorbed by our atmosphere at lower levels.
Some exceedingly interesting experiments might be made by means of a telescope having a prism attached to its objective extremity, and furnished with a micrometer, because by it the difference of the illumination of objects might be determined with extreme accuracy—as for example, the comparative intensity between the bright and dark parts of the moon, the comparative intensity of the solar light reflected by the moon, and the lumière cendré, or the light of the earth reflected on the moon, whence a comparison might be made between the light of the sun and that of the earth. Hence also it might be known whether the terrestrial hemispheres successively visible from the moon are more or less luminous, according as they contain more land or water, and at the same time it might be possible to appreciate the more or less cloudy or clear state of our atmosphere, so that in time we might ultimately find in the lumière cendré of the moon data upon the mean diaphaneity of different terrestrial hemispheres which are of different temperatures.
It is found by experience that heat is developed in opaque and translucent substances by their absorption of solar light, but that the sun’s rays do not sensibly alter the temperature of perfectly transparent bodies through which they pass. As the temperature of the pellucid planetary space can be but little affected by the passage of the sun’s light and heat, neither can it be sensibly raised by the heat now radiated from the earth.
Doubtless the radiation of all the bodies in the universe maintains the ethereal medium at a higher temperature than it would 228otherwise have, and must eventually increase it, but by a quantity so evanescent that it is hardly possible to conceive a time when a change will become perceptible.
The temperature of space being so low as -239° Fahrenheit, it becomes a matter of no small interest to ascertain whether the earth may not be ultimately reduced by radiation to the temperature of the surrounding medium; what the sources of heat are; and whether they be sufficient to compensate the loss, and to maintain the earth in a state fit for the support of animal and vegetable life in time to come. All observations that have been made under the surface of the ground concur in proving that there is a stratum at the depth of from 40 to 100 feet throughout the whole earth where the temperature is invariable at all times and seasons, and which differs but little from the mean annual temperature of the country above. According to M. Boussingault, that stratum at the equator is at the depth of little more than a foot in places sheltered from the direct rays of the sun; but in our climates it is at a much greater depth. In the course of more than half a century the temperature of the earth at the depth of 90 feet, in the cellars of the Observatory at Paris, has never been above or below 53° of Fahrenheit’s thermometer, which is only 2° above the mean annual temperature at Paris. This zone, unaffected by the sun’s rays from above, or by the internal heat from below, serves as an origin whence the effects of the external heat are estimated on one side, and the internal temperature of the globe on the other.
As early as the year 1740 M. Gensanne discovered in the lead-mines of Giromagny, in the Vosges mountains, three leagues from Béfort, that the heat of the ground increases with the depth below the zone of constant temperature. A vast number of observations have been made since that time, in the mines of Europe and America, by MM. Saussure, Daubuisson, Humboldt, Cordier, Fox, Reich, and others, which agree, without an exception, in proving that the temperature of the earth becomes higher in descending towards its centre. The greatest depth that has been attained is in the silver-mine of Guanaxato, in Mexico, where M. de Humboldt found a temperature of 98° at the depth of 285 fathoms, the mean annual temperature of the country being only 61°. Next to that is the Dalcoath copper-mine, in Cornwall, where Mr. Fox’s thermometer stood at 68° in a hole in the rock at the 229depth of 230 fathoms, and at 82° in water at the depth of 240 fathoms, the mean annual temperature at the surface being about 50°. But it is needless to multiply examples, all of which concur in showing that there is a very great difference between the temperature in the interior of the earth and at its surface. Mr. Fox’s observations on the temperature of springs which rise at profound depths in mines afford the strongest testimony. He found considerable streams flowing into some of the Cornish mines at the temperature of 80° or 90°, which is about 30° or 40° above that of the surface, and also ascertained that nearly 2,000,000 gallons of water are daily pumped from the bottom of the Poldice mine, which is 176 fathoms deep at 90° or 100°. As this is higher than the warmth of the human body, Mr. Fox justly observes that it amounts to a proof that the increased temperature cannot proceed from the persons of the workmen employed in the mines. Neither can the warmth of mines be attributed to the condensation of the currents of air which ventilate them. Mr. Fox, whose opinion is of high authority in these matters, states that, even in the deepest mines, the condensation of the air would not raise the temperature more than 5° or 6°; and that, if the heat could be attributed to this cause, the seasons would sensibly affect the temperature of mines, which it appears they do not where the depth is great. Besides, the Cornish mines are generally ventilated by numerous shafts opening into the galleries from the surface or from a higher level. The air circulates freely in these, descending in some shafts and ascending in others. In all cases Mr. Fox found that the upward currents are of a higher temperature than the descending currents; so much so, that in winter the moisture is often frozen in the latter to a considerable depth; the circulation of air, therefore, tends to cool the mine instead of increasing the heat. Mr. Fox has also removed the objections arising from the comparatively low temperature of the water in the shafts of abandoned mines, by showing that observations in them, from a variety of circumstances which he enumerates, are too discordant to furnish any conclusion as to the actual heat of the earth. The high temperature of mines might be attributed to the effects of the fires, candles, and gunpowder used by the miners, did not a similar increase obtain in deep wells, and in borings to great depths in search of water, where no such causes 230of disturbance occur. In a well dug with a view to discover salt in the canton of Berne, and long deserted, M. de Saussure had the most complete evidence of increasing heat. The same has been confirmed by the temperature of many wells, both in France and England, especially by the Artesian wells, so named from a peculiar method of raising water first resorted to in Artois, and since become very general. An Artesian well consists of a shaft a few inches in diameter, bored into the earth till a spring is found. To prevent the water being carried off by the adjacent strata, a tube is let down which exactly fills the bore from top to bottom, in which the water rises pure to the surface. It is clear the water could not rise unless it had previously descended from high ground through the interior of the earth to the bottom of the well. It partakes of the temperature of the strata through which it passes, and in every instance has been warmer in proportion to the depth of the well; but it is evident that the law of increase cannot be obtained in this manner. Perhaps the most satisfactory experiments on record are those made by MM. Auguste de la Rive and F. Marcet during the year 1833, in a boring for water about a league from Geneva, at a place 318 feet above the level of the lake. The depth of the bore was 727 feet, and the diameter only between four and five inches. No spring was ever found; but the shaft filled with mud, from the moisture of the ground mixing with the earth displaced in boring, which was peculiarly favourable for the experiments, as the temperature at each depth may be considered to be that of the particular stratum. In this case, where none of the ordinary causes of disturbance could exist, and where every precaution was employed by scientific and experienced observers, the temperature was found to increase regularly and uniformly with the depth at the rate of about 1° of Fahrenheit for every 52 feet. Professor Reich of Freyberg has found that the mean of a great number of observations both in mines and wells is 1° of Fahrenheit for every 55 feet of depth; and from M. Arago’s observations in the Grenelle Artesian well at Paris, the increase is 1° of Fahrenheit for every 45 feet. Though there can be no doubt as to the increase of temperature in penetrating the crust of the earth, there is still much uncertainty as to the law of increase, which varies with the nature of the soil and other local circumstances; but, on an average, it has been 231estimated at the rate of 1° for every 50 or 60 feet, which corresponds with the observations of MM. Marcet and De la Rive. In consequence of the rapid increase of internal heat, thermal springs, or such as are independent of volcanic action, rising from a great depth, must necessarily be very rare and of a high temperature; and it is actually found that none are so low as 68° of Fahrenheit; that of Chaudes Aigues, in Auvergne, is about 136°. In many places warm water from Artesian wells will probably come into use for domestic purposes, and it is even now employed in manufactories near Stutgardt, in Alsace, &c.
It is hardly to be expected that at present any information with regard to the actual internal temperature of the earth should be obtained from that of the ocean, on account of the mobility of fluids, by which the colder masses sink downwards, while those that are warmer rise to the surface. Nevertheless, it may be stated that the temperature of the sea decreases with the depth between the tropics; while, on the contrary, all our northern navigators found that the temperature increases with the depth in the polar seas. The change takes place about the 70th parallel of latitude. Some ages hence, however, it may be known whether the earth has arrived at a permanent state as to heat, by comparing secular observations of the temperature of the ocean if made at a great distance from the land.
Should the earth’s temperature increase at the rate of 1° for every 50 feet, it is clear that at the depth of 200 miles the hardest substances must be in a state of fusion, and our globe must in that case either be encompassed by a stratum of melted lava at that depth, or it must be a ball of liquid fire 7600 miles in diameter, enclosed in a thin coating of solid matter; for 200 miles are nothing when compared with the size of the earth. No doubt the form of the earth, as determined by the pendulum and arcs of the meridian, as well as by the motions of the moon, indicates original fluidity and subsequent consolidation and reduction of temperature by radiation; but whether the law of increasing temperature is uniform at still greater depths than those already attained by man, it is impossible to say. At all events, internal fluidity is not inconsistent with the present state of the earth’s surface, since earthy matter is as bad a conductor of heat as lava, which often retains its heat at a very 232little depth for years after its surface is cool. Whatever the radiation of the earth might have been in former times, certain it is that it goes on very slowly in our days; for M. Fourier has computed that the central heat is decreasing from radiation by only about the 1⁄30000th part of a degree in a century. If so, there can be no doubt that it will ultimately be dissipated; but as far as regards animal and vegetable life, it is of very little consequence whether the centre of our planet be liquid fire or ice, since its condition in either case could have no sensible effect on the climate at its surface. The internal fire does not even impart heat enough to melt the snow at the poles, though nearer to the centre than any other part of the globe.
The immense extent of active volcanic fire is one of the causes of heat which must not be overlooked.
The range of the Andes from Chile to the north of Mexico, probably from Cape Horn to Behring Straits, is one vast district of igneous action, including the Caribbean and the West Indian Islands on one hand; and stretching quite across the Pacific Ocean, through the Polynesian Archipelago, the New Hebrides, the Georgian and Friendly Islands, on the other. Another chain begins with the Aleutian Islands, extends to Kamtschatka, and from thence passes through the Kurile, Japanese, and Philippine Islands, to the Moluccas, whence it spreads with terrific violence through the Indian Archipelago, even to the Bay of Bengal. Volcanic action may again be followed from the entrance of the Persian Gulf to Madagascar, Bourbon, the Canaries, and Azores. Thence a continuous igneous region extends through about 1000 geographical miles to the Caspian Sea, including the Mediterranean, and extending north and south between the 35th and 40th parallels of latitude; and in central Asia a volcanic region occupies 2500 square geographical miles. The volcanic fires are developed in Iceland in tremendous force; and the antarctic land discovered by Sir James Ross is an igneous formation of the boldest structure, where a volcano in high activity rises 12,000 feet above the perpetual ice of these polar deserts, and within 191⁄2° of the south pole. Throughout this vast portion of the world the subterraneous fire is often intensely active, producing such violent earthquakes and eruptions that their effects, accumulated during millions of years, may account for many of the great geological 233changes of igneous origin that have already taken place in the earth, and may occasion others not less remarkable, should time—that essential element in the vicissitudes of the globe—be granted, and their energy last.
Sir Charles Lyell, who has shown the power of existing causes with great ingenuity, estimates that on an average twenty eruptions take place annually in different parts of the world; and many must occur or have happened, even on the most extensive and awful scale, among people equally incapable of estimating their effects and of recording them. We should never have known the extent of the fearful eruption which took place in the island of Sumbawa, in 1815, but for the accident of Sir Stamford Raffles having been governor of Java at the time. It began on the 5th of April, and did not entirely cease till July. The ground was shaken through an area of 1000 miles in circumference; the tremors were felt in Java, the Moluccas, a great part of Celebes, Sumatra, and Borneo. The detonations were heard in Sumatra, at the distance of 970 geographical miles in a straight line; and at Ternate, 720 miles in the opposite direction. The most dreadful whirlwinds carried men and cattle into the air; and with the exception of 26 persons, the whole population of the island perished to the amount of 12,000. Ashes were carried 300 miles to Java in such quantities that the darkness during the day was more profound than ever had been witnessed in the most obscure night. The face of the country was changed by the streams of lava, and by the upheaving and sinking of the soil. The town of Tomboro was submerged, and water stood to the depth of 18 feet in places which had been dry land. Ships grounded where they had previously anchored, and others could hardly penetrate the mass of cinders which floated on the surface of the sea for several miles to the depth of two feet. A catastrophe similar to this, though of less magnitude, took place in the island of Bali in 1808, which was not heard of in Europe till years afterwards. The eruption of Coseguina in the Bay of Fonseca, which began on the 19th of January, 1835, and lasted many days, was even more dreadful and extensive in its effects than that of Sumbawa. The ashes during this eruption were carried by the upper current of the atmosphere as far north as Chiassa, which is upwards of 400 leagues to the windward of that volcano. Many volcanoes supposed to be extinct have all 234at once burst out with inconceivable violence. Witness Vesuvius, on historical record; and the volcano in the island of St. Vincent in our own days, whose crater was lined with large trees, and which had not been active in the memory of man. Vast tracts are of volcanic origin where volcanoes have ceased to exist for ages. Whence it may be inferred that in some places the subterraneous fires are in the highest state of activity, in some they are inert, and in others they appear to be extinct. Yet there are few countries that are not subject to earthquakes of greater or less intensity; the tremors are propagated like a sonorous undulation to such distances that it is impossible to say in what point they originate. In some recent instances their power must have been tremendous. In South America, so lately as 1822, an area of 100,000 square miles, which is equal in extent to the half of France, was raised several feet above its present level—a most able account of which is given in the ‘Transactions of the Geological Society,’ by an esteemed friend of the author’s, the late Mrs. Graham, who was present during the whole time of that formidable earthquake, which recurred at short intervals for more than two months, and who possessed talents to appreciate, and had opportunities of observing, its effects under the most favourable circumstances at Valparaiso, and for miles along the coast where it was most intense. A considerable elevation of the land has again taken place along the coast of Chile, in consequence of the violent earthquake which happened on the 20th of February, 1835. In 1819 a ridge of land stretching for 50 miles across the delta of the Indus, 16 feet broad, was raised 10 feet above the plain. The reader is referred to Sir Charles Lyell’s excellent ‘Principles of Geology,’ already mentioned, for most interesting details of the phenomena and extensive effects of volcanoes and earthquakes, too numerous to find a place here. It may however be mentioned that innumerable earthquakes are from time to time shaking the solid crust of the globe, and carrying destruction to distant regions, progressively though slowly accomplishing the great work of change. A most disastrous instance took place on the 15th of December, 1857, in the Neapolitan provinces of La Basilicata and Principato Citeriore, where the destruction was extensive and terrible; the number of victims, according to the official accounts, being 235returned at upwards of ten thousand. These terrible engines of ruin, fitful and uncertain as they may seem, must, like all durable phenomena, have a law which may in time be discovered by long-continued and accurate observations.
The shell of volcanic fire that girds the globe at a small depth below our feet has been attributed to different causes. By some it is supposed to originate in an ocean of incandescent matter, still existing in the central abyss of the earth. Some conceive it to be superficial, and due to chemical action, in strata at no very great depth when compared with the size of the globe. The more so as matter on a most extensive scale is passing from old into new combinations, which, if rapidly effected, are capable of producing the most intense heat. According to others, electricity, which is so universally diffused in all its forms throughout the earth, if not the immediate cause of the volcanic phenomena, at least determines the chemical affinities that produce them. It is clear that a subject so involved in mystery must give rise to much speculation, in which every hypothesis is attended with difficulties that observation alone can remove.
But the views of Mr. Babbage and Sir John Herschel on the general cause of volcanic action, and the changes in the equilibrium of the internal heat of the globe, accord more with the laws of mechanics and radiant heat than any that have been proposed. The theory of these distinguished philosophers, formed independently of each other, is equally consistent with observed phenomena, whether the earth be a solid crust encompassing a nucleus of liquid lava, or that there is merely a vast reservoir or stratum of melted matter at a moderate depth below the superficial crust. The author is indebted to the kindness of Sir Charles Lyell for the perusal of a most interesting letter from Sir John Herschel, in which he states his views on the subject.
Supposing that the globe is merely a solid crust, resting upon fluid or semi-fluid matter, whether extending to the centre or not, the transfer of pressure from one part of its surface to another by the degradation of existing continents, and the formation of new ones, would be sufficient to subvert the equilibrium of heat in the interior, and occasion volcanic eruptions. For, since the internal heat of the earth is transmitted outwards by radiation, an accession of new matter on any part of the surface, like an addition of clothing, by keeping it in, would raise the 236temperature of the strata below, and in the course of ages would even reduce those at a great depth to a state of fusion. Some of the substances might be converted into gases; and should the accumulation of new matter take place at the bottom of the sea, as is generally the case, this lava would be mixed with water in a state of ignition in consequence of the enormous pressure of the ocean, and of the newly superimposed matter which would prevent it from expanding into steam. Now Sir Charles Lyell has shown, with his usual talent, that the quantity of matter carried down by rivers from the surface of the continents is comparatively trifling, and that the great transfer to the bottom of the ocean is produced at the coast-line by the action of the sea; hence, says Sir John Herschel, “the greatest accumulation of local pressure is in the central area of the deep sea, while the greatest local relief takes place along the abraded coast-lines. Here then should occur the chief volcanic vents.” As the crust of the earth is much weaker on the coasts than elsewhere, it is more easily ruptured, and, as Mr. Babbage observes, immense rents might be produced there by its contraction in cooling down after being deprived of a portion of its original thickness. The pressure on the bottom of the ocean would force a column of lava mixed with ignited water and gas to rise through an opening thus formed, and, says Sir John Herschel, “when the column attains such a height that the ignited water can become steam, the joint specific gravity of the column is suddenly diminished, and up comes a jet of mixed steam and lava, till so much has escaped that the matter deposited at the bottom of the ocean takes a fresh bearing, when the evacuation ceases and the crack becomes sealed up.”
This theory perfectly accords with the phenomena of nature, since there are very few active volcanoes at a distance from the sea, and the exceptions that do occur are generally near lakes, or they are connected with volcanoes on the maritime coasts. Many break out even in the bottom of the ocean, probably owing to some of the supports of the superficial crust giving way, so that the steam and lava are forced up through the fissures.
Finally, Mr. Babbage observes that, “in consequence of changes continually going on, by the destruction of forests, the filling up of seas, the wearing down of elevated lands, the heat radiated from the earth’s surface varies considerably at different 237periods. In consequence of this variation, and also in consequence of the covering up of the bottom of the sea by the detritus of the land, the surfaces of equal temperature within the earth are continually changing their form, and exposing thick beds near the exterior to alterations of temperature. The expansion and contraction of these strata may form rents and veins, produce earthquakes, determine volcanic eruptions, elevate continents, and, possibly, raise mountain chains.”
The numerous vents for the internal heat formed by volcanoes, hot springs, and the emission of steam, so frequent in volcanic regions, no doubt maintain the tranquillity of the interior fluid mass, which seems to be perfectly inert unless when put in motion by unequal pressure.
But, to whatever cause the increasing heat of the earth and the subterranean fires may ultimately be referred, it is certain that, except in some local instances, they have no sensible effect on the temperature of its surface. It may therefore be concluded that the heat of the earth, above the zone of uniform temperature, is entirely owing to the sun.
The power of the solar rays depends much upon the manner in which they fall, as we readily perceive from the different climates on our globe. Although the sun is about three millions of miles nearer to the earth in winter than in summer, his rays strike the atmosphere in the northern hemisphere so obliquely that it absorbs a much greater quantity of heat than when they are more direct (N. 217). Indeed it is so great that, when the sun has an altitude of 30°, one half of his heat is absorbed by the atmosphere, and it increases very rapidly as he sinks towards the horizon. However, that heat is not lost: it is most beneficial to the earth, being really the heat which supplies the greatest part of that which is radiated into space during the absence of the sun. Professor Dove has shown, by taking at all seasons the mean of the temperatures of points on the earth’s surface diametrically opposite to each other, that the average temperature of the whole earth’s surface in June, when we are farthest from the sun, considerably exceeds that in December, when we are nearest to him, owing to the excess of water in the southern hemisphere, and that of land in the northern, which gives a general insular climate to the former, and a continental climate to the latter.
The observations of the north polar navigators, and those of 238Sir John Herschel at the Cape of Good Hope, show that the direct heating influence of the solar rays is greatest at the equator, and that it diminishes gradually as the latitude increases. At the equator the maximum is 483⁄4°, while in Europe it has never exceeded 291⁄2°.
M. Pouillet has estimated with singular ingenuity, from a series of observations made by himself, that the whole quantity of heat which the earth receives annually from the sun is such as would be sufficient to melt a stratum of ice covering the whole globe 46 feet deep. Part of this heat is radiated back into space; but by far the greater part descends into the earth during the summer, towards the zone of uniform temperature, whence it returns to the surface in the course of the winter, and tempers the cold of the ground and the atmosphere in its passage to the ethereal regions, where it is lost, or rather where it combines with the radiation from the other bodies of the universe in maintaining the temperature of space. The sun’s power being greatest between the tropics, the heat sinks deeper there than elsewhere, and the depth gradually diminishes towards the poles; but the heat is also transmitted laterally from the warmer to the colder strata north and south of the equator, and aids in tempering the severity of the polar regions.
The mean heat of the earth, above the stratum of constant temperature, is determined from that of springs; and, if the spring be on elevated ground, the temperature is reduced by computation to what it would be at the level of the sea, assuming that the heat of the soil varies according to the same law as the heat of the atmosphere, which is about 1° of Fahrenheit’s thermometer for every 333·7 feet. From a comparison of the temperature of numerous springs with that of the air, Sir David Brewster concludes that there is a particular line passing nearly through Berlin, at which the temperature of springs and that of the atmosphere coincide; that in approaching the arctic circle the temperature of springs is always higher than that of the air, while, proceeding towards the equator, it is lower.
Since the warmth of the superficial strata of the earth decreases from the equator to the poles, there are many places in both hemispheres where the ground has the same mean temperature. If lines were drawn through all those points in the upper strata of the globe which have the same mean annual temperature, 239they would be nearly parallel to the equator between the tropics, and would become more and more irregular and sinuous towards the poles. These are called isogeothermal lines. A variety of local circumstances disturb their parallelism, even between the tropics.
The temperature of the ground at the equator is lower on the coasts and islands than in the interior of continents; the warmest part is in the interior of Africa; but it is obviously affected by the nature of the soil, especially if it be volcanic.
Much has been done to ascertain the manner in which heat is distributed over the surface of our planet, and the variations of climate, which, in a general view, mean every change of the atmosphere, such as of temperature, humidity, variations of barometric pressure, purity of air, the serenity of the heavens, the effects of winds, and electric tension. Temperature depends upon the property which all bodies possess, more or less, of perpetually absorbing and emitting or radiating heat. When the interchange is equal, the temperature of a body remains the same; but, when the radiation exceeds the absorption, it becomes colder, and vice versâ. In order to determine the distribution of heat over the surface of the earth, it is necessary to find a standard by which the temperature in different latitudes may be compared. For that purpose it is requisite to ascertain, by experiment, the mean temperature of the day, of the month, and of the year, at as many places as possible throughout the earth. The annual average temperature may be found by adding the mean temperatures of all the months in the year, and dividing the sum by twelve. The average of ten or fifteen years will give it approximately; for, although the temperature in any place maybe subject to very great variations, yet it never deviates more than a few degrees from its mean state, which consequently offers a good standard of comparison. As a standard, however, much greater accuracy is required.
If climate depended solely upon the heat of the sun, all places having the same latitude would have the same mean annual temperature. The motion of the sun in the ecliptic, indeed, occasions perpetual variations in the length of the day, and in the direction of the rays with regard to the earth; yet, as the cause is periodic, the mean annual temperature from the sun’s motion alone must be constant in each parallel of latitude; for it is 240evident that the accumulation of heat in the long days of summer, which is but little diminished by radiation during the short nights, is balanced by the small quantity of heat received during the short days in winter, and its radiation in the long, frosty, and clear nights. In fact, if the globe were everywhere on a level with the surface of the sea, and of uniform substance, so as to absorb and radiate heat equally, the mean heat of the sun would be regularly distributed over its surface in zones of equal annual temperature parallel to the equator, from which it would decrease to each pole as the square of the cosine of the latitude; and its quantity would only depend upon the altitude of the sun and atmospheric currents. The distribution of heat, however, in the same parallel, is very irregular in all latitudes except between the tropics, where the isothermal lines, or the lines passing through places of equal mean annual temperature, are more nearly parallel to the equator. The causes of disturbance are very numerous; but such as have the greatest influence, according to M. de Humboldt, to whom we are indebted for the greater part of what is known on the subject, are the elevation of the continents, the distribution of land and water over the surface of the globe exposing different absorbing and radiating powers; the variations in the surface of the land, as forests, sandy deserts, verdant plains, rocks, &c.; mountain-chains covered with masses of snow, which diminish the temperature; the reverberation of the sun’s rays in the valleys, which increases it; and the interchange of currents, both of air and water, which mitigates the rigour of climates; the warm currents from the equator softening the severity of the polar frosts, and the cold currents from the poles tempering the intense heat of the equatorial regions. To these may be added cultivation, though its influence extends over but a small portion of the globe, only a fourth part of the land being inhabited.
Temperature decreases with the height above the level of the sea, as well as with the latitude. The air in the higher regions of the atmosphere is much cooler than that below, because the warm air expands as it rises, by which its capacity for heat is increased, a great proportion becomes latent or absorbed, and less of it sensible. A portion of air at the surface of the earth whose temperature is 70° of Fahrenheit, if carried to the height of two miles and a half, would expand so much that its temperature 241would be reduced 50°; and in the ethereal regions the temperature is 239° below the zero point of Fahrenheit.
The height at which snow lies perpetually decreases from the equator to the poles, and is higher in summer than in winter; but it varies from many circumstances. Snow rarely falls when the cold is intense and the atmosphere dry. Extensive forests produce moisture by their evaporation; and high table-lands, on the contrary, dry and warm the air, because the air at great elevations is too rare to absorb much of the sun’s heat. In the Cordilleras of the Andes, plains of only twenty-five square leagues from their extent raise the temperature as much as 3° or 4° above what is found at the same altitude on the rapid declivity of a mountain, consequently the line of perpetual snow varies according as one or other of these causes prevails. Aspect in general has also a great influence; yet the line of perpetual snow is much higher on the northern than on the southern side of the Himalaya, partly because the air is nearly deprived of its moisture by precipitation before it arrives at the northern side of the mountains. On the whole, it appears that the mean height between the tropics at which the snow lies perpetually is about 15,207 feet above the level of the sea; whereas snow does not cover the ground continually at the level of the ocean till near the north pole. In the southern hemisphere, however, the cold is greater than in the northern. In Sandwich Land, between the 54th and 58th degrees of latitude, perpetual snow and ice extend to the sea-level; and in the island of S. Georgia, in the 53rd degree of south latitude, which corresponds with the latitude of the central counties of England, perpetual snow descends even to the level of the ocean. It has been shown that this excess of cold in the southern hemisphere cannot be attributed to the winter being longer than ours by 73⁄4 days. It is probably owing to the open sea surrounding the south pole, which permits the icebergs to descend to a lower latitude by 10° than they do in the northern hemisphere, on account of the numerous obstructions opposed to them by the islands and continents about the north pole. Icebergs from the Arctic seas seldom float farther to the south than the Azores; whereas those that come from the south pole descend to as low a latitude as that of the Cape of Good Hope.
The influence of mountain-chains does not wholly depend upon the line of perpetual congelation. They attract and condense 242the vapours floating in the air, and send them down in torrents of rain. They radiate heat into the atmosphere at a lower elevation, and increase the temperature of the valleys by the reflection of the sun’s rays, and by the shelter they afford against prevailing winds. But, on the contrary, one of the most general and powerful causes of cold arising from the vicinity of mountains is the freezing currents of wind which rush from their lofty peaks along the rapid declivities, chilling the surrounding valleys: such is the cutting north wind called the bise in Switzerland.
Next to elevation, the difference in the radiating and absorbing powers of the sea and land has the greatest influence in disturbing the regular distribution of heat. The extent of the dry land is not above the fourth part of that of the ocean; so that the general temperature of the atmosphere, regarded as the result of the partial temperatures of the whole surface of the globe, is most powerfully modified by the sea. Besides, the ocean acts more uniformly on the atmosphere than the diversified surface of the solid mass does, both by the equality of its curvature and its homogeneity. In opaque substances the accumulation of heat is confined to the stratum nearest the surface. The seas become less heated at their surface than the land, because the solar rays, before being extinguished, penetrate the transparent liquid to a greater depth and in greater numbers than in the opaque masses. On the other hand, water has a considerable radiating power, which, together with evaporation, would reduce the surface of the ocean to a very low temperature, if the cold particles did not sink to the bottom on account of their superior density. The seas preserve a considerable portion of the heat they receive in summer, and from their saltness do not freeze so soon as fresh water. So that, in consequence of all these circumstances, the ocean is not subject to such variations of heat as the land, and, by imparting its temperature to the winds and by its currents, it diminishes the rigour of climate on the coasts and in the islands, which are never subject to such extremes of heat and cold as are experienced in the interior of continents, though they are liable to fogs and rain from the evaporation of the adjacent seas. On each side of the equator to the 48th degree of latitude, the surface of the ocean is in general warmer than the air above it. The mean of the difference of the temperature 243at noon and midnight is about 1°·37, the greatest deviation never exceeding from 0°·36 to 2°·16, which is much cooler than the air over the land.
On land the temperature depends upon the nature of the soil and its products, its habitual moisture or dryness. From the eastern extremity of the Sahara desert quite across Africa, the soil is almost entirely barren sand; and the Sahara desert itself extends over an area of 194,000 square leagues, equal to twice the area of the Mediterranean Sea, and raises the temperature of the air by radiation from 90° to 100°, which must have a most extensive influence. On the contrary, vegetation cools the air by evaporation and the apparent radiation of cold from the leaves of plants, because they absorb more caloric than they give out. The graminiferous plains of South America cover an extent ten times greater than France, occupying no less than about 50,000 square leagues, which is more than the whole chain of the Andes, and all the scattered mountain-groups of Brazil. These, together with the plains of North America and the steppes of Europe and Asia, must have an extensive cooling effect on the atmosphere if it be considered that in calm and serene nights they cause the thermometer to descend 12° or 14°, and that in the meadows and heaths in England the absorption of heat by the grass is sufficient to cause the temperature to sink to the point of congelation during the night for ten months in the year. Forests cool the air also by shading the ground from the rays of the sun, and by evaporation from the boughs. Hales found that the leaves of a single plant of helianthus three feet high exposed nearly forty feet of surface; and, if it be considered that the woody regions of the river Amazons, and the higher part of the Orinoco, occupy an area of 260,000 square leagues, some idea may be formed of the torrents of vapour which rise from the leaves of the forests all over the globe. However, the frigorific effects of their evaporation are counteracted in some measure by the perfect calm which reigns in the tropical wildernesses. The innumerable rivers, lakes, pools, and marshes interspersed through the continents absorb caloric, and cool the air by evaporation; but, on account of the chilled and dense particles sinking to the bottom, deep water diminishes the cold of winter, so long as ice is not formed.
In consequence of the difference in the radiating and absorbing powers of the sea and land, their configuration greatly modifies 244the distribution of heat over the surface of the globe. Under the equator only one-sixth part of the circumference is land; and the superficial extent of land in the northern and southern hemispheres is in the proportion of three to one. The effect of this unequal division is greater in the temperate than in the torrid zones, for the area of land in the northern temperate zone is to that in the southern as thirteen to one, whereas the proportion of land between the equator and each tropic is as five to four. It is a curious fact, noticed by Mr. Gardner, that only one twenty-seventh part of the land of the globe has land diametrically opposite to it. This disproportionate arrangement of the solid part of the globe has a powerful influence on the temperature of the southern hemisphere. But, besides these greater modifications, the peninsulas, promontories, and capes, running out into the ocean, together with bays and internal seas, all affect temperature. To these may be added the position of continental masses with regard to the cardinal points. All these diversities of land and water influence temperature by the agency of the winds. On this account the temperature is lower on the eastern coasts both of the New and Old World than on the western; for, considering Europe as an island, the general temperature is mild in proportion as the aspect is open to the Atlantic Ocean, the superficial temperature of which, as far north as the 45th and 50th degrees of latitude, does not fall below 48° or 51° of Fahrenheit, even in the middle of winter. On the contrary, the cold of Russia arises from its exposure to the northern and eastern winds. But the European part of that empire has a less rigorous climate than the Asiatic, because it does not extend to so high a latitude.
The interposition of the atmosphere modifies all the effects of the sun’s heat. The earth communicates its temperature so slowly, that M. Arago has occasionally found as much as from 14° to 18° of difference between the heat of the soil and that of the air two or three inches above it.
The circumstances which have been enumerated, and many more, concur in disturbing the regular distribution of heat over the globe, and occasion numberless local irregularities. Nevertheless the mean annual temperature becomes gradually lower from the equator to the poles. But the diminution of mean heat is most rapid between the 40th and 45th degrees of latitude both 245in Europe and America, which accords perfectly with theory; whence it appears that the variation in the square of the cosine of the latitude (N. 127), which expresses the law of the change of temperature, is a maximum towards the 45th degree of latitude. The mean annual temperature under the equator in America is about 811⁄2° of Fahrenheit: in Africa it is said to be nearly 83°. The difference probably arises from the winds of Siberia and Canada, whose chilly influence is sensibly felt in Asia and America, even within 18° of the equator.
The isothermal lines are nearly parallel to the equator, till about the 22nd degree of latitude on each side of it, where they begin to lose their parallelism, and continue to do so more and more as the latitude augments. With regard to the northern hemisphere, the isothermal line of 59° of Fahrenheit passes between Rome and Florence in latitude 43°; and near Raleigh in North Carolina, latitude 36°: that of 50° of equal annual temperature runs through the Netherlands, latitude 51°; and near Boston in the United States, latitude 421⁄2°. that of 41° passes near Stockholm, latitude 591⁄2°; and St. George’s Bay, Newfoundland, latitude 48°: and lastly, the line of 32°, the freezing point of water, passes between Ulea in Lapland, latitude 66°, and Table Bay, on the coast of Labrador, latitude 54°.
Thus it appears that the isothermal lines, which are nearly parallel to the equator for about 22°, afterwards deviate more and more. From observations made during the numerous voyages in the Arctic Seas, it is found that the isothermal lines of Europe and America entirely separate in the high latitudes, and surround two poles of maximum cold: one, in 79° N. lat. and 120° E. long., has a mean temperature of 2° Fahrenheit; and the other, whose temperature was determined by Sir David Brewster to be 31⁄2° Fahrenheit, from the observations of Sir Edward Parry is near Melville Island. The pole of the earth’s rotation, whose mean temperature is probably not below 15° Fahrenheit, is nearly midway between the two; and the line which joins these points of maximum cold is almost coincident with that diameter of the polar basin which bisects it, and passes through its two great outlets into the Pacific and Atlantic Oceans, a most remarkable feature, and strongly indicative of the absence of land, and of the prevalence of a materially milder 246climate in the polar Ocean, probably not under 15° Fahrenheit.[12] It is believed that two corresponding poles of maximum cold exist in the southern hemisphere, though observations are wanting to trace the course of the southern isothermal lines with the same accuracy as the northern.
The isothermal lines, or such as pass through places where the mean annual temperature of the air is the same, do not always coincide with the isogeothermal lines, which are those passing through places where the mean temperature of the ground is the same. Sir David Brewster, in discussing this subject, finds that the isogeothermal lines are always parallel to the isothermal lines; consequently the same general formula will serve to determine both, since the difference is a constant quantity obtained by observation, and depending upon the distance of the place from the neutral isothermal line. These results are confirmed by the observations of M. Kupffer of Kasan during his excursions to the north, which show that the European and the American portions of the isogeothermal line of 32° of Fahrenheit actually separate, and go round the two poles of maximum cold. This traveller remarked, also, that the temperature both of the air and of the soil decreases most rapidly towards the 45th degree of latitude.
It is evident that places may have the same mean annual temperature, and yet differ materially in climate. In one, the winters may be mild and the summers cool; whereas another may experience the extremes of heat and cold. Lines passing through places having the same mean summer or winter temperature are neither parallel to the isothermal, the geothermal lines, nor to one another, and they differ still more from the parallels of latitude. In Europe, the latitude of two places which have the same annual heat never differs more than 8° or 9°; whereas the difference in the latitude of those having the same mean winter temperature is sometimes as much as 18° or 19°. At Kasan, in the interior of Russia, in latitude 55°·48, nearly the same with that of Edinburgh, the mean annual temperature is about 37°·6; at Edinburgh it is 47°·84. At Kasan the mean summer temperature is 64°·84, and that of winter 2°·12; whereas 247at Edinburgh the mean summer temperature is 58°·28, and that of winter 38°·66. Whence it appears that the difference of winter temperature is much greater than that of summer. At Quebec the summers are as warm as those in Paris, and grapes sometimes ripen in the open air: whereas the winters are as severe as in Petersburgh; the snow lies five feet deep for several months, wheel carriages cannot be used, the ice is too hard for skating, travelling is performed in sledges, and frequently on the ice of the river St. Lawrence. The cold at Melville Island on the 15th of January, 1820, according to Sir Edward Parry, was 55° below the zero of Fahrenheit’s thermometer; and when Dr. Kane was on the northern coast of Greenland it was 70° below that point; yet the summer heat during the day in these high latitudes is insupportable.
Observations tend to prove that all the climates of the earth are stable, and that their vicissitudes are only periods or oscillations of more or less extent, which vanish in the mean annual temperature of a sufficient number of years. This constancy of the mean annual temperature of the different places on the surface of the globe shows that the same quantity of heat which is annually received by the earth is annually radiated into space; and that would be the case even if the quantity of heat emitted by the sun should vary with his spots, for, if more were received, more would be radiated. Nevertheless, a variety of causes may disturb the climate of a place; cultivation may make it warmer; but it is at the expense of some other place, which becomes colder in the same proportion. There may be a succession of cold summers and mild winters, but in some other country the contrary takes place to effect the compensation; wind, rain, snow, fog, and the other meteoric phenomena, are the ministers employed to accomplish the changes. The distribution of heat may vary with a variety of circumstances; but the absolute quantity lost and gained by the whole earth in the course of a year, if not invariably the same, is at least periodical.
Influence of Temperature on Vegetation—Vegetation varies with the Latitude and Height above the Sea—Geographical Distribution of Land Plants—Distribution of Marine Plants—Corallines, Shell-fish, Reptiles, Insects, Birds, and Quadrupeds—Varieties of Mankind, yet identity of Species.
The gradual decrease of temperature in the air and in the earth, from the equator to the poles, is clearly indicated by its influence on vegetation. In the valleys of the torrid zone, where the mean annual temperature is very high, and where there is abundance of light and moisture, nature adorns the soil with all the luxuriance of perpetual summer. The palm, the bombax ceiba, and a variety of magnificent trees, tower to the height of 150 or 200 feet above the banana, the bamboo, the arborescent fern, and numberless other tropical productions, so interlaced by creeping and parasitical plants, as often to present an impenetrable barrier. But the richness of vegetation gradually diminishes with the temperature; the splendour of the tropical forest is succeeded by the regions of the vine and olive; these again yield to the verdant meadows of more temperate climes; then follow the birch and the pine, which probably owe their existence in very high latitudes more to the warmth of the soil than to that of the air. But even these enduring plants become dwarfish shrubs, till a verdant carpet of mosses and lichens, enamelled with flowers, exhibits the last sign of vegetable life during the short but fervid summers at the polar regions. Such is the effect of cold and diminished light on the vegetable kingdom, that the number of species growing under the equator and in the northern latitudes of 45° and 68° are in the proportion of the numbers 12, 4, and 1. Notwithstanding the remarkable difference between a tropical and polar flora, light and moisture seem to be almost the only requisites for vegetation, since neither heat, cold, nor even comparative darkness, absolutely destroy the fertility of nature. In salt plains and sandy deserts alone hopeless barrenness prevails. 249Plants grow on the borders of hot springs: they form the oases wherever moisture exists among the burning sands of Africa; they are found in caverns almost void of light, though generally blanched and feeble. The ocean teems with vegetation. The snow itself not only produces a red lichen, discovered by Saussure in the frozen declivities of the Alps, found in abundance by the author crossing the Col de Bonhomme from Savoy to Piedmont, and by the polar navigators in the Arctic regions, but it affords shelter to the productions of these inhospitable climes against the piercing winds that sweep over fields of everlasting ice. Those undaunted mariners narrate that under this cold defence plants spring up, dissolve the snow a few inches round, and the part above, being again quickly frozen into a transparent sheet of ice, admits the sun’s rays, which warm and cherish the plants in this natural hothouse, till the returning summer renders such protection unnecessary.
The chemical action of light is, however, absolutely requisite for the growth of plants which derive their principal nourishment from the atmosphere. They consume the carbonic acid gas, nitrogen, aqueous vapour, and ammonia it contains; but it is the chemical agency of light that enables them to absorb, decompose, and consolidate these substances into wood, leaves, flowers, and fruit. The atmosphere would soon be deprived of these elements of vegetable life were they not perpetually supplied by the animal creation; while, in return, plants decompose the moisture they imbibe, and, having assimilated the carbonic acid gas, they exhale oxygen for the maintenance of the animated creation, and thus preserve a just equilibrium. Hence it is the combined and powerful influences of the whole solar beams that give such brilliancy to the tropical forests, while, with their decreasing energy in the higher latitudes, vegetation becomes less vigorous. On that account it is vain to expect that the fruit and flowers raised in our hothouses can ever have the flavour, perfume, or colouring equal to that which they acquire from the vivid light of their native skies.
By far the greater number of the known species of plants are indigenous in equinoctial America; Europe contains about half the number; Asia, with its islands, somewhat less than Europe; Australia, with the islands in the Pacific, still less; and in Africa there are fewer known vegetable productions than in any 250part of the globe of equal extent, for that rich and luxuriant region discovered by Dr. Livingstone has yet to be explored botanically. Very few social plants, such as grasses and heaths that cover large tracts of land, are to be found between the tropics, except on the sea-coasts and elevated plains. Some exceptions to this, however, are to be met with in the jungles of the Deccan, &c. In the equatorial regions, where the heat is always great, the distribution of plants depends upon the mean annual temperature; whereas in temperate zones the distribution is regulated in some degree by the summer heat. Some plants require a gentle heat of long continuance, others flourish most where the extremes of heat and cold are greater. The range of wheat is very great; it may be cultivated as far north as the 60th degree of latitude; but in the torrid zone it will seldom form an ear below an elevation of 4500 feet above the level of the sea from exuberance of vegetation; nor will it ripen generally above the height of 12,000 feet; in Tibet it ripens at a still greater elevation. Colonel Sykes states that in the Deccan wheat thrives as low as 1800 feet above the sea. The best wines are produced between the 30th and 45th degrees of north latitude. With regard to the vegetable kingdom, elevation is equivalent to latitude as far as temperature is concerned. In ascending the mountains of the torrid zone, the richness of the tropical vegetation diminishes with the height; a succession of plants similar to, though not identical with, those found in latitudes of corresponding mean temperature takes place; the lofty forests by degrees lose their splendour; stunted shrubs succeed; till at last the progress of the lichen is checked by perpetual snow. On the volcano of Teneriffe there are five successive zones, each producing distinct families of plants. The first is the region of vines, the next that of laurels; these are followed by the region of pines, of Ericas or heaths, of grass; the whole covering the declivity of the peak through an extent of 11,200 feet of perpendicular height.
Near the equator oaks flourish at the height of 9200 feet above the sea; and, on the lofty range of the Himalaya, the primula, the convallaria, and the veronica flower, but not the primrose, the lily of the valley, or the veronica, which adorn our meadows; for, although the herbarium collected by Moorcroft, on his route from Neetee to Daba and Gartope in Chinese Tartary, 251at elevations as high or even higher than Mont Blanc, abound in Alpine and European genera, the species are universally different, with the single exception of the Rhodiola rosea, which is identical with the species that blooms in Scotland. It is not in this instance alone that similarity of climate obtains without identity of productions; throughout the whole globe a certain analogy both of structure and appearance is frequently discovered between plants under corresponding circumstances which are yet specifically different. It is even said that a difference of 25° of latitude occasions a total change, not only of vegetable productions, but of organised beings. Certain it is that each separate region both of land and water, from the frozen shores of the polar circles to the burning regions of the torrid zone, possesses a flora peculiarly its own. The whole globe has been divided by physical geographers into various botanical districts, differing almost entirely in their specific vegetable productions, the limits of which are most decided when they are separated by a wide expanse of ocean, mountain chains, sandy deserts, salt plains, or internal seas. A considerable number of plants are common to the northern regions of Asia, Europe, and America, where the continents almost unite; but, in approaching the south, the floras of these three great divisions of the globe differ more and more even in the same parallels of latitude, which shows that temperature alone is not the cause of the almost complete diversity of species that everywhere prevails. The floras of China, Siberia, Tartary, of the European district including central Europe and the coast of the Mediterranean, and the Oriental region comprising the countries round the Black and Caspian Seas, all differ in specific character. Only twenty-four species were found by MM. Humboldt and Bonpland in Equinoctial America identical with those of the Old World; and Dr. Robert Brown not only found that a peculiar vegetation exists in Australia between the 33rd and 35th parallels of south latitude, but that at the eastern and western extremities of these parallels not one species is common to both, and that certain genera also are almost entirely confined to these spots. The number of species common to Australia and Europe are only 166 out of 4100, and probably some of these have been conveyed thither by the colonists; but the greater part of that continent is still unexplored. However, this proportion exceeds what has 252hitherto been observed in southern Africa, and, from what has been already stated, the proportion of European species in Equinoctial America is still less.
Islands partake of the vegetation of the nearest continents; but, when very remote from land, their floras are altogether peculiar. The Aleutian Islands, extending between Asia and America, partake of the vegetation of the northern parts of both continents, and may have served as a chain of communication. In Madeira and Teneriffe, the plants of Portugal, Spain, the Azores, and of the northern coast of Africa, are found; and the Canaries contain a great number of plants belonging to the African coast. But each of these islands possesses a flora that exists nowhere else; and St. Helena, standing alone in the midst of the Atlantic Ocean, produces only two or three species of plants recognised as belonging to any other part of the world.
It appears from the investigations of M. de Humboldt that between the tropics the plants, such as grasses and palms, which have only one seed-lobe, are to the tribe which have two seed-lobes, like most of the European species, in the proportion of one to four; in the temperate zones they are as one to six; and in the Arctic regions, where mosses and lichens, which form the lowest order of the vegetable creation, abound, the proportion is as one to two. Annuals with one and two seed-lobes, in the temperate zones, amount to one-sixth of the whole, omitting the cryptogamia (N. 218); in the torrid zone they scarcely form one-twentieth, and in Lapland one-thirtieth part. In approaching the equator the ligneous exceed the number of herbaceous plants; in America there are 120 different species of forest trees, whereas in the same latitudes in Europe only 34 are to be found.
Similar laws regulate the distribution of marine plants. Groups of algæ, or marine plants, affect particular temperatures or zones of latitude and different depths, though some few genera prevail throughout the ocean. The polar Atlantic basin to the 40th degree of north latitude presents a well-defined vegetation. The West India seas, including the Gulf of Mexico, the eastern coast of South America, the Indian Ocean and its gulfs, the shores of New Holland, and the neighbouring islands, have each their distinct species. The Mediterranean possesses a vegetation peculiar to itself, extending to the Black Sea; and the species of marine plants on the coast of Syria and in the port of Alexandria differ 253almost entirely from those of Suez and the Red Sea. It is observed that shallow seas have a different set of plants from such as are deeper and colder; and, unlike terrestrial vegetation, the algæ are more numerous in the mean latitudes than either towards the equator or the poles. They vary also with the depth: completely different kinds affect different depths, their seeds being of such specific gravity as to remain and germinate where the parent plant grew. The quantity of algæ in that accumulation known as the sargassa or grassy sea is so great, that the early navigators, Columbus and Lerius, compared it to extensively inundated meadows: it impeded their ships, and alarmed their sailors. It is in the North Atlantic, a little to the west of the meridian of Fayal, one of the Azores, between the 25th and 36th parallels of latitude. A smaller bank lies between the 22nd and 26th degrees of north latitude, about 80 leagues west of the meridian of the Bahama Islands. These masses chiefly consist of one or two species of sargassa, the most extensive genus of the order Fucoideæ.
Some of the seaweeds grow to enormous lengths, and all are highly coloured, though many of them must grow in deep water. Light, however, may not be the only principle on which the colour of vegetables depends, since Baron Humboldt met with green plants growing in complete darkness in one of the mines at Freyberg.
In the dark and tranquil caves of the ocean, on the shores alternately covered and deserted by the restless waves, on the lofty mountain and extended plain, in the chilly regions of the north, and in the genial warmth of the south, specific diversity is a general law of the vegetable kingdom, which cannot be accounted for by diversity of climate; and yet the similarity, though not identity, of species is such, under the same isothermal lines, that if the number of species belonging to one of the great families of plants be known in any part of the globe, the whole number of the flowering or more perfect plants, and also the number of species composing the other vegetable families, may be estimated with considerable accuracy.
Various opinions have been formed on the original or primitive distribution of plants over the face of the globe; but, since botanical geography has become a science, the phenomena observed 254have led to the conclusion that vegetable creation must have taken place in a number of distinctly different centres, as the islands and continents rose above the ocean, each of which was the original seat of a certain number of peculiar species which at first grew there and nowhere else. Heaths are exclusively confined to the Old World; and no indigenous rose-tree has ever been seen in the New, the whole southern hemisphere being destitute of that beautiful and fragrant plant. But this is still more confirmed by multitudes of particular plants, having an entirely local and insulated existence, growing spontaneously in some particular spot, and in no other place: for example, the cedar of Lebanon, which grows indigenously on that mountain, and in no other part of the world. On the other hand, as there can be no doubt that many races of plants have been extinguished, Sir John Herschel thinks it possible that these solitary instances may be the last surviving remnants of the same group universally disseminated, but in course of extinction, or that perhaps two processes may be going on at the same time:—“Some groups may be spreading from their foci, others retreating to their last holds.”
The same laws obtain in the distribution of the animal creation. Even the microscopic existences, which seem to be the most widely spread, have their specific localities; and the zoophyte (N. 219), occupying the next lowest place in animated nature, is widely scattered through the seas of the torrid zone, each species being confined to the district and depth best suited to its wants. Mollusks, or the animals of shells, decrease in size and beauty with their distance from the equator; and not only each sea and every basin of the ocean, but each depth, is inhabited by its peculiar tribe of fish. Indeed, MM. Peron and Le Sueur assert that, among the many thousands of marine animals which they had examined, there is not a single animal of the southern regions which is not distinguishable by essential characters from the analogous species in the northern seas.
Reptiles are not exempt from the general law. The saurian (N. 220) tribes of the four quarters of the globe differ in species; and, although warm countries abound in venomous snakes, they are specifically different in different localities, and decrease both in numbers and in the virulence of their poison 255with decrease of temperature. The dispersion of insects necessarily follows that of the vegetables which supply their food; and in general it is observed that each kind of plant is peopled by its peculiar inhabitants. Each species of bird has its peculiar haunt, notwithstanding the locomotive powers of the winged tribes. The emu is confined to Australia, the condor to the Andes and their declivities, and the bearded vulture or lemmergeyer to the Alps. Some birds, like the common sparrow, have a wide range; but those met with in every country are few in number. Quadrupeds are distributed in the same manner wherever man has not interfered. Such as are indigenous in one country are not the same with their congeners in another; and, with the exception of some kind of bats, no mammiferous animal is indigenous in the Polynesian Archipelago, nor in any of the islands on the borders of the central part of the Pacific.
In reviewing the infinite variety of organised beings that people the surface of the globe, nothing is more remarkable than the distinctions which characterise the different tribes of mankind, from the ebony skin of the torrid zone to the fair and ruddy complexion of the Scandinavian—a difference which existed in the earliest recorded times, since the African is represented in the sacred writings to have been as black as he is at the present day, and the most ancient Egyptian paintings confirm that truth; yet it appears, from a comparison of the principal circumstances relating to the animal economy or physical character of the various tribes of mankind, that the different races are identical in species. Many attempts have been made to trace the various tribes back to a common origin, by collating the numerous languages which are or have been spoken. Some classes of these have few or no words in common, yet exhibit a remarkable analogy in the laws of their grammatical construction. The languages spoken by the native American nations afford examples of these; indeed, the refinement in the grammatical construction of the tongues of the American savages leads to the belief that they must originally have been spoken by a much more civilised class of mankind. Some tongues have little or no resemblance in structure, though they correspond extensively in their vocabularies, as the Syrian dialects. In all these cases it may be inferred that the nations speaking the languages 256in question descended from the same stock; but the probability of a common origin is much greater in the Indo-European nations, whose languages, such as the Sanscrit, Greek, Latin, German, &c., have an affinity both in structure and correspondence of vocables. In many tongues not the smallest resemblance can be traced; length of time, however, may have obliterated original identity; but so many ages have passed before the subject became a study, and so many languages have worn out of use, that it may be doubted whether any satisfactory result will ever be arrived at with regard to the original speech of mankind.
Terrestrial Heat—Radiation—Transmission—Melloni’s experiments—Heat in Solar Spectrum—Polarization of Heat—Nature of Heat—Absorptions—Dew—Rain—Combustion—Expansion—Compensation Pendulum—Transmission through Crystals—Propagation—Dynamic Theory of Heat—Mechanical equivalent of Heat—Latent Heat is the Force of Expansion—Steam—Work performed by Heat—Conservation of Force—Mechanical Power in the Tides—Dynamical Power of Light—Analogy between Light, Heat, and Sound.
That heat producing rays exist independently of those of light is a matter of constant experience in the abundant emission of them from boiling water. They dart in divergent straight lines from flame and from each point in the surfaces of hot bodies, in the same manner as diverging rays of light proceed from every point of those that are luminous. According to the experiments of Sir John Leslie, radiation proceeds not only from the surface of substances, but also from the particles at a minute depth below it. He found that the emission is most abundant in a direction perpendicular to the radiating surface, and that it is more rapid from a rough than from a polished surface: radiation, however, can only take place in air and in vacuo; it is altogether imperceptible when the hot body is enclosed in a solid or liquid. Heated substances, when exposed to the open air, continue to radiate heat till they become nearly of the temperature of the surrounding medium. The radiation is very rapid at first, but diminishes according to a known law with the temperature of the heated body. It appears, also, that the radiating power of a surface is inversely as its reflecting power; and bodies that are most impermeable to heat radiate least. Substances, however, have an elective power, only reflecting heat of a certain refrangibility. Mr. Grove gives paper, snow, and lime as instances, which, although all white, radiate heat of different refrangibilities, while metals, whatever their colour may be, radiate all kinds alike.
Rays of heat, whether they proceed from the sun, from flame, or other terrestrial sources, luminous or non-luminous, are instantaneously 258transmitted through solid and liquid substances, there being no appreciable difference in the time they take to pass through layers of any nature or thickness whatever. They pass also with the same facility whether the media be agitated or at rest; and in these respects the analogy between light and heat is perfect. Radiant heat passes through the gases with the same facility as light; but a remarkable difference obtains in the transmission of light and heat through most solid and liquid substances, the same body being often perfectly permeable to the luminous, and altogether impermeable to the calorific rays. For example, thin and perfectly transparent plates of alum and citric acid sensibly transmit all the rays of light from an argand lamp, but stop eight or nine tenths of the concomitant heat; whilst a large piece of brown rock-crystal gives a free passage to the radiant heat, but intercepts almost all the light. Alum united to green glass is also capable of transmitting the brightest light, but it gives not the slightest indication of heat; while rock-salt covered thickly over with soot, so as to be perfectly opaque to light, transmits a considerable quantity of heat. M. Melloni has established the general law in uncrystallized substances such as glass and liquids, that the property of instantaneously transmitting heat is in proportion to their refractive powers. The law, however, is entirely at fault in bodies of a crystalline texture. Carbonate of lead, for instance, which is colourless, and possesses a very high refractive power with regard to light, transmits less radiant heat than Iceland spar or rock-crystal, which are very inferior to it in the order of refrangibility; whilst rock-salt, which has the same transparency and refractive power with alum and citric acid, transmits six or eight times as much heat. This remarkable difference in the transmissive power of substances having the same appearance is attributed by M. Melloni to their crystalline form, and not to the chemical composition of their molecules, as the following experiments prove. A block of common salt cut into plates entirely excludes calorific radiation; yet, when dissolved in water, it increases the transmissive power of that liquid: moreover, the transmissive power of water is increased in nearly the same degree, whether salt or alum be dissolved in it; yet these two substances transmit very different quantities of heat in their solid state. Notwithstanding the influence of crystallization on the transmissive power of 259bodies, no relation has been traced between that power and the crystalline form.
The transmission of radiant heat is analogous to that of light through coloured media. When common white light passes through a red liquid, almost all the more refrangible rays, and a few of the red, are intercepted by the first layer of the fluid; fewer are intercepted by the second, still less by the third, and so on: till at last the losses become very small and invariable, and those rays alone are transmitted which give the red colour to the liquid. In a similar manner, when plates of the same thickness of any substance, such as glass, are exposed to an argand lamp, a considerable portion of the radiant heat is arrested by the first plate, a less portion by the second, still less by the third, and so on, the quantity of lost heat decreasing till at last the loss becomes a constant quantity. The transmission of radiant heat through a solid mass follows the same law. The losses are very considerable on first entering it, but they rapidly diminish in proportion as the heat penetrates deeper, and become constant at a certain depth. Indeed, the only difference between the transmission of radiant heat through a solid mass, or through the same mass when cut into plates of equal thickness, arises from the small quantity of heat that is reflected at the surface of the plates. It is evident, therefore, that the heat gradually lost is not intercepted at the surface, but absorbed in the interior of the substance, and that heat which has passed through one stratum of air experiences a less absorption in each of the succeeding strata, and may therefore be propagated to a greater distance before it is extinguished. The experiments of M. de Laroche show that glass, however thin, totally intercepts the obscure rays of heat when they flow from a body whose temperature is lower than that of boiling water; that, as the temperature increases, the calorific rays are transmitted more and more abundantly; and, when the body becomes highly luminous, that they penetrate the glass with perfect ease. The extreme brilliancy of the sun is probably the reason why his heat, when brought to a focus by a lens, is more intense than any that has been produced artificially. It is owing to the same cause that glass screens, which entirely exclude the heat of a common fire, are permeable by the solar heat.
The results obtained by M. de Laroche have been confirmed 260by the experiments of M. Melloni on heat radiated from sources of different temperatures, whence it appears that the calorific rays pass less abundantly not only through glass, but through rock-crystal, Iceland spar, and other diaphanous bodies, both solid and liquid, according as the temperature of their origin is diminished, and that they are altogether intercepted when the temperature is about that of boiling water.
In fact, he has proved that the heat emanating from the sun or from a bright flame consists of rays which differ from each other as much as the coloured rays do which constitute white light. This explains the reason of the loss of heat as it penetrates deeper and deeper into a solid mass, or in passing through a series of plates; for, of the different kinds of rays which dart from a vivid flame, all are successively extinguished by the absorbing nature of the substance through which they pass, till those homogeneous rays alone remain which have the greatest facility in passing through that particular substance; exactly as in a red liquid the violet, blue, green, orange, and yellow rays are extinguished, and the red are transmitted.
M. Melloni employed four sources of heat, two of which were luminous and two obscure; namely, an oil-lamp without a glass, incandescent platina, copper heated to 696°, and a copper vessel filled with water at the temperature of 1781⁄2° of Fahrenheit. Rock-salt transmitted heat in the proportion of 92 rays out of 100 from each of these sources; but all other substances pervious to radiant heat, whether solid or liquid, transmitted more heat from sources of high temperature than from such as are low. For instance, limpid and colourless fluate of lime transmitted in the proportion of 78 rays out of 100 from the lamp, 69 from the platina, 42 from the copper, and 33 from the hot water; while transparent rock-crystal transmitted 38 rays in 100 from the lamp, 28 from the platina, 6 from the copper, and 9 from the hot water. Pure ice transmitted only in the proportion of 6 rays in the 100 from the lamp, and entirely excluded those from the other three sources. Out of 39 different substances, 34 were pervious to the calorific rays from hot water, 14 excluded those from the hot copper, and 4 did not transmit those from the platinum.
Thus it appears that heat proceeding from these four sources is of different kinds: this difference in the nature of the calorific 261rays is also proved by another experiment, which will be more easily understood from the analogy of light. Red light, emanating from red glass, will pass in abundance through another piece of red glass, but it will be absorbed by green glass; green rays will more readily pass through a green medium than through one of any other colour. This holds with regard to all colours; so in heat. Rays of heat of the same intensity, which have passed through different substances, are transmitted in different quantities by the same piece of alum, and are sometimes stopped altogether; showing that rays which emanate from different substances possess different qualities. It appears that a bright flame furnishes rays of heat of all kinds, in the same manner as it gives light of all colours; and, as coloured media transmit some coloured rays and absorb the rest, so bodies transmit some rays of heat and exclude the others. Rock-salt alone resembles colourless transparent media in transmitting all kinds of heat, even that of the hand, just as they transmit white light, consisting of rays of all colours. Radiant heat is unequally refracted by a prism of rock-salt like light, and the rays of heat thus dispersed are found to possess properties analogous to the rays of the coloured spectrum.
The property of transmitting the calorific rays diminishes to a certain degree with the thickness of the body they have to traverse, but not so much as might be expected. A piece of very transparent alum transmitted three or four times less radiant heat from the flame of a lamp than a piece of nearly opaque quartz about a hundred times as thick. However, the influence of thickness upon the phenomena of transmission increases with the decrease of temperature in the origin of the rays, and becomes very great when that temperature is low. This is a circumstance intimately connected with the law established by M. de Laroche; for M. Melloni observed that the difference between the quantities of heat transmitted by the same plate of glass, exposed successively to several sources of heat, diminished with the thinness of the plate, and vanished altogether at a certain limit; and that a film of mica transmitted the same quantity of heat, whether it was exposed to incandescent platinum or to a mass of iron heated to 360°.
Coloured glasses transmit rays of light of certain degrees of refrangibility, and absorb those of other degrees. For example, 262red glass absorbs the more refrangible rays, and transmits the red, which are the least refrangible. On the contrary, violet glass absorbs the least refrangible, and transmits the violet, which are the most refrangible. Now M. Melloni has found, that, although the colouring matter of glass diminishes its power of transmitting heat, yet red, orange, yellow, blue, violet, and white glass transmit calorific rays of all degrees of refrangibility; whereas green glass possesses the peculiar property of transmitting the least refrangible calorific rays, and stopping those that are most refrangible. It has therefore the same elective action for heat that coloured glass has for light, and its action on heat is analogous to that of red glass on light. Alum and sulphate of lime are exactly opposed to green glass in their action on heat, by transmitting the most refrangible rays with the greatest facility.
The heat which has already passed through green or opaque black glass will not pass through alum, whilst that which has been transmitted through glasses of other colours traverses it readily.
By reversing the experiment, and exposing different substances to heat that had already passed through alum, M. Melloni found that the heat emerging from alum is almost totally intercepted by opaque substances, and is abundantly transmitted by all such as are transparent and colourless, and that it suffers no appreciable loss when the thickness of the plate is varied within certain limits. The properties of the heat therefore which issues from alum nearly approach to those of light and solar heat.
Radiant heat in traversing various media is not only rendered more or less capable of being transmitted a second time, but, according to the experiments of Professor Powell, it becomes more or less susceptible of being absorbed in different quantities by black or white surfaces.
M. Melloni has proved that solar heat contains rays which are affected by different substances in the same way as if the heat proceeded from a terrestrial source; whence he concludes that the difference observed between the transmission of terrestrial and solar heat arises from the circumstance of solar heat containing all kinds of heat, whilst in other sources some of the kinds are wanting.
Radiant heat, from sources of any temperature whatever, is 263subject to the same laws of reflection and refraction as rays of light. The index of refraction from a prism of rock-salt, determined experimentally, is nearly the same for light and heat.
Liquids, the various kinds of glass, and probably all substances, whether solid or liquid, that do not crystallize regularly, are more pervious to the calorific rays according as they possess a greater refractive power. For example, the chloride of sulphur, which has a high refractive power, transmits more of the calorific rays than the oils, which have a less refractive power: oils transmit more radiant heat than the acids; the acids more than aqueous solutions; and the latter more than pure water, which of all the series has the least refractive power, and is the least pervious to heat. M. Melloni observed also that each ray of the solar spectrum follows the same law of action with that of terrestrial rays having their origin in sources of different temperatures; so that the very refrangible rays may be compared to the heat emanating from a focus of high temperature, and the least refrangible to the heat which comes from a source of low temperature. Thus, if the calorific rays emerging from a prism be made to pass through a layer of water contained between two plates of glass, it will be found that these rays suffer a loss in passing through the liquid as much greater as their refrangibility is less. The rays of heat that are mixed with the blue or violet light pass in great abundance, while those in the obscure part which follows the red light are almost totally intercepted. The first, therefore, act like the heat of a lamp, and the last like that of boiling water.
These circumstances explain the phenomena observed by several philosophers with regard to the point of greatest heat in the solar spectrum, which varies with the substance of the prism. Sir William Herschel, who employed a prism of flint glass, found that point to be a little beyond the red extremity of the spectrum; but, according to M. Seebeck, it is found to be upon the yellow, upon the orange, on the red, or at the dark limit of the red, according as the prism consists of water, sulphuric acid, crown or flint glass. If it be recollected that, in the spectrum from crown glass, the maximum heat is in the red part, and that the solar rays, in traversing a mass of water, suffer losses inversely as their refrangibility, it will be easy to understand the reason of the phenomenon in question. The solar heat which 264comes to the anterior face of the prism of water consists of rays of all degrees of refrangibility. Now, the rays possessing the same index of refraction with the red light suffer a greater loss in passing through the prism than the rays possessing the refrangibility of the orange light, and the latter lose less in their passage than the heat of the yellow. Thus the losses, being inversely proportional to the degree of refrangibility of each ray, cause the point of maximum heat to tend from the red towards the violet, and therefore it rests upon the yellow part. The prism of sulphuric acid, acting similarly, but with less energy than that of water, throws the point of greatest heat on the orange; for the same reason, the crown and flint glass prisms transfer that point respectively to the red and to its limit. M. Melloni, observing that the maximum point of heat is transferred farther and farther towards the red end of the spectrum, according as the substance of the prism is more and more permeable to heat, inferred that a prism of rock-salt, which possesses a greater power of transmitting the calorific rays than any known body, ought to throw the point of greatest heat to a considerable distance beyond the visible part of the spectrum,—an anticipation which experiment fully confirmed, by placing it as much beyond the dark limits of the red rays as the red part is distant from the blueish green band of the spectrum.
In all these experiments M. Melloni employed a thermomultiplier,—an instrument that measures the intensity of the transmitted heat with an accuracy far beyond what any thermometer ever attained. It is a very elegant application of M. Seebeck’s discovery of thermo-electricity; but the description of this instrument is reserved for a future occasion, because the principle on which it is constructed has not yet been explained.
In the beginning of the present century, not long after M. Malus had discovered the polarization of light, he and M. Berard proved that the heat which accompanies the sun’s light is capable of being polarized; but their attempts totally failed with heat derived from terrestrial, and especially from non-luminous sources. M. Berard, indeed, imagined that he had succeeded; but, when his experiments were repeated by Mr. Lloyd and Professor Powell, no satisfactory result could be obtained. M. Melloni resumed the subject, and endeavoured to effect the polarization of heat by tourmaline, as in the case of light. It was 265already shown that two slices of tourmaline, cut parallel to the axis of the crystal, transmit a great portion of the incident light when looked through with their axes parallel, and almost entirely exclude it when they are perpendicular to one another. Should radiant heat be capable of polarization, the quantity transmitted by the slices of tourmaline in their former position ought greatly to exceed that which passes through them in the latter, yet M. Melloni found that the quantity of heat was the same in both cases: whence he inferred that heat from a terrestrial source is incapable of being polarized. Professor Forbes of Edinburgh, who prosecuted this subject with great acuteness and success, came to the same conclusion in the first instance; but it occurred to him, that, as the pieces of tourmaline became heated by being very near the lamp, the secondary radiation from them rendered the very small difference in the heat that was transmitted in the two positions of the pieces of tourmaline imperceptible. Nevertheless he succeeded in proving, by numerous observations, that heat from various sources is polarized by the tourmaline; but that the effect with non-luminous heat is very minute and difficult to perceive, on account of the secondary radiation. Though light is almost entirely excluded in one position of the pieces of tourmaline, and transmitted in the other, a vast quantity of radiant heat passes through them in all positions. Eighty-four per cent. of the heat from an argand lamp passed through them in the case where light was altogether stopped. It is only the difference in the quantity of transmitted heat that gives evidence of its polarization. The second slice of tourmaline, when perpendicular to the first, stops all the light, but transmits a great proportion of heat; alum, on the contrary, stops almost all the heat, and transmits the light; whence it may be concluded that heat, though intimately partaking the nature of light, and accompanying it under certain circumstances, as in reflection and refraction, is capable of almost complete separation from it under others. The separation has since been perfectly effected by M. Melloni, by passing a beam of light through a combination of water and green glass, coloured by the oxide of copper. Even when the transmitted light was concentrated by lenses, so as to render it almost as brilliant as the direct light of the sun, it showed no sensible heat.
Professor Forbes next employed two bundles of laminæ of 266mica, placed at the polarizing angle, and so cut that the plane of incidence of the heat corresponded with one of the optic axes of this mineral. The heat transmitted through this apparatus was polarized from a source whose temperature was even as low as 200°; heat was also polarized by reflection; but the experiments, though perfectly successful, are more difficult to conduct.
It appears, from the various experiments of M. Melloni and Professor Forbes, that all the calorific rays emanating from the sun and terrestrial sources are equally capable of being polarized by reflection and by refraction, whether double or single, and that they are also capable of circular polarization by all the methods employed in the circular polarization of light. Plates of quartz cut at right angles to the axis of the prism possess the property of turning the calorific rays in one direction, while other plates of the same substance from a differently modified prism cause the rays to rotate in the contrary direction; and two plates combined, when of different affection, and of equal thickness, counteract each other’s effects as in the case of light. Tourmaline separates the heat into two parts, one of which it absorbs, while it transmits the other; in short, the transmission of radiant heat is precisely similar to that of light.
Since heat is polarized in the same manner as light, it may be expected that polarized heat transmitted through doubly refracting substances should be separated into two pencils, polarized in planes at right angles to each other; and that when received on an analyzing plate they should interfere and produce invisible phenomena, perfectly analogous to those described in Section XXII. with regard to light (N. 221).
It was shown, in the same section, that if light polarized by reflection from a pane of glass be viewed through a plate of tourmaline, with its longitudinal section vertical, an obscure cloud, with its centre wholly dark, is seen on the glass. When, however, a plate of mica uniformly about the thirteenth of an inch in thickness is interposed between the tourmaline and the glass, the dark spot vanishes, and a succession of very splendid colours are seen; and, as the mica is turned round in a plane perpendicular to the polarized ray, the light is stopped when the plane containing the optic axis of the mica is parallel or perpendicular to the plane of polarization. Now, instead of light, if heat from 267a non-luminous source be polarized in the manner described, it ought to be transmitted and stopped by the interposed mica under the same circumstances under which polarized light would be transmitted or stopped. Professor Forbes found that this is really the case, whether he employed heat from luminous or non-luminous sources: and he had evidence, also, of circular and elliptical polarization of heat. It therefore follows, that if heat were visible, under similar circumstances we should see figures perfectly similar to those given in Note 213, and those following; and, as these figures are formed by the interference of undulations of light, it may be inferred that heat, like light, is propagated by undulations of the ethereal medium, which interfere under certain conditions, and produce figures analogous to those of light. It appears also, from Mr. Forbes’s experiments, that the undulations of heat are longer than the undulations of light; and it has already been mentioned that Professor Draper considers them to be normal, like those of sound.
That light and heat are both vibrations of the ethereal medium is not the less true on account of the rays of heat being unseen, for the condition of visibility or invisibility may only depend upon the construction of our eyes, and not upon the nature of the motion which produces these sensations in us. The sense of seeing may be confined within certain limits. The chemical rays beyond the violet end of the spectrum may be too rapid, or not sufficiently excursive, in their vibrations, to be visible to the human eye; and the calorific rays beyond the other end of the spectrum may not be sufficiently rapid, or too extensive, in their undulations, to affect our optic nerves, though both may be visible to certain animals or insects. We are altogether ignorant of the perceptions which direct the carrier-pigeon to his home, or of those in the antennæ of insects which warn them of the approach of danger; nor can we understand the telescopic vision which directs the vulture to his prey before he himself is visible even as a speck in the heavens. So, likewise, beings may exist on earth, in the air, or in the waters, which hear sounds our ears are incapable of hearing, and which see rays of light and heat of which we are unconscious. Our perceptions and faculties are limited to a very small portion of that immense chain of existence which extends from the Creator to evanescence.
The identity of action under similar circumstances is one of 268the strongest arguments in favour of the common nature of the chemical, visible, and calorific rays. They are all capable of reflection from polished surfaces, of refraction through diaphanous substances, of polarization by reflection and by doubly refracting crystals; their velocity is prodigious; they may be concentrated and dispersed by convex and concave mirrors; they pass with equal facility through rock-salt and are capable of radiation; and they are subject to the same law of interference with those of light: hence there can be no doubt that the whole assemblage of rays visible and invisible which constitute a solar beam are propagated by the undulations of the ethereal medium, and consequently as motions they come under the same laws of analysis.
When radiant heat falls upon a surface, part of it is reflected and part of it is absorbed; consequently, the best reflectors possess the least absorbing powers. The temperature of very transparent fluids is not raised by the passage of the sun’s rays, because they do not absorb any of them; and, as his heat is very intense, transparent solids arrest a very small portion of it. The absorption of the sun’s rays is the cause both of the colour and temperature of solid bodies. A black substance absorbs all the rays of light, and reflects none; and since it absorbs, at the same time, all the calorific rays, it becomes sooner warm, and rises to a higher temperature, than bodies of any other colour. Blue bodies come next to black in their power of absorption. And, since substances of a blue tint absorb all the other colours of the spectrum, they absorb by far the greatest part of the calorific rays, and reflect the blue where they are least abundant. Next in order come the green, yellow, red, and, last of all, white bodies, which reflect nearly all the rays both of light and heat. However, there are certain limpid and colourless media, which in some cases intercept calorific radiations and become heated, while in other cases they transmit them and undergo no change of temperature.
All substances may be considered to radiate heat, whatever their temperature may be, though with different intensities, according to their nature, the state of their surfaces, and the temperature of the medium into which they are brought. But every surface absorbs as well as radiates heat; and the power of absorption is always equal to that of radiation; for, under the same circumstances, matter which becomes soon warm also cools 269rapidly. There is a constant tendency to an equal diffusion of heat, since every body in nature is giving and receiving it at the same instant; each will be of uniform temperature when the quantities of heat given and received during the same time are equal—that is, when a perfect compensation takes place between each and all the rest. Our sensations only measure comparative degrees of heat: when a body, such as ice, appears to be cold, it imparts fewer calorific rays than it receives; and when a substance seems to be warm—for example, a fire—it gives more heat than it takes. The phenomena of dew and hoar-frost are owing to this inequality of exchange; the heat radiated during the night by substances on the surface of the earth, into a clear expanse of sky, is lost to us, and no return is made from the blue vault, so that their temperature sinks below that of the air, whence they abstract a part of that heat which holds the atmospheric humidity in solution, and a deposition of dew takes place. If the radiation be great, the dew is frozen and becomes hoar-frost, which is the ice of dew. Cloudy weather is unfavourable to the formation of dew, by preventing the free radiation of heat; and actual contact is requisite for its deposition, since it is never suspended in the air like fog. Plants derive a great part of their nourishment from this source; and, as each possesses a power of radiation peculiar to itself, they are capable of procuring a sufficient supply for their wants. The action of the chemical rays imparts to all substances more or less the power of condensing vapour on those parts on which they fall, and must therefore have a considerable influence on the deposition of dew. There may be a low degree of humidity in the air which may yet contain a great quantity of aqueous vapour, for vapour while it exists as gas is dry. The temperature at which the atmosphere can contain no more vapour without precipitation is called the dew point, and is measured by the hygrometer. In foretelling the changes of weather it is scarcely inferior to the barometer.
Steam is formed throughout the whole mass of a boiling liquid, whereas evaporation takes place only at the free surface of liquids, and that under the ordinary temperature and pressure of the atmosphere. There is a constant evaporation from the land and water all over the earth. The rapidity of the formation does not depend altogether on the dryness of the air; according to Dr. Dalton’s experiments, it depends also on the difference 270between the tension of the vapour which is forming, and that which is already in the atmosphere. In calm weather vapour accumulates in the stratum of air immediately above the evaporating surface, and retards the formation of more; whereas a strong wind accelerates the process by carrying off the vapour as soon as it rises, and making way for a succeeding portion of dry air.
Rain is formed by the mixing of two masses of air of different temperatures; the colder part, by abstracting from the other the heat which holds it in solution, occasions the particles to approach each other and form drops of water, which, becoming too heavy to be sustained by the atmosphere, sink to the earth by gravitation in the form of rain. The contact of two strata of air of different temperatures, moving rapidly in opposite directions, occasions an abundant precipitation of rain. When the masses of air differ very much in temperature, and meet suddenly, hail is formed. This happens frequently in hot plains near a ridge of mountains, as in the south of France, from the sudden descent of an intensely cold current of wind into a mass of air nearly saturated with vapour. Such also is the cause of the severe hail-storms which occasionally take place on extensive plains within the tropics.
An accumulation of heat invariably produces light: with the exception of the gases, all bodies which can endure the requisite degree of heat without decomposition begin to emit light at the same temperature; but, when the quantity of heat is so great as to render the affinity of their component particles less than their affinity for the oxygen of the atmosphere, a chemical combination takes place with the oxygen, light and heat are evolved, and fire is produced. Combustion—so essential for our comfort, and even existence—takes place very easily from the small affinity between the component parts of atmospheric air, the oxygen being nearly in a free state; but, as the cohesive force of the particles of different substances is very variable, different degrees of heat are requisite to produce their combustion. The tendency of heat to a state of equal diffusion or equilibrium, either by radiation or contact, makes it necessary that the chemical combination which occasions combustion should take place instantaneously; for, if the heat were developed progressively, it would be dissipated by degrees, and would never 271accumulate sufficiently to produce a temperature high enough for the evolution of flame.
It is a general law that all bodies expand by heat and contract by cold. The expansive force of heat has a constant tendency to overcome the attraction of cohesion, and to separate the constituent particles of solids and fluids; by this separation the attraction of aggregation is more and more weakened, till at last it is entirely overcome, or even changed into repulsion. By the continual addition of heat, solids may be made to pass into liquids, and from liquids to the aëriform state, the dilatation increasing with the temperature; and every substance expands according to a law of its own. Gases expand more than liquids, and liquids more than solids. The expansion of air is more than eight times that of water, and the increase in the bulk of water is at least forty-five times greater than that of iron. Metals dilate uniformly from the freezing to the boiling points of the thermometer; the uniform expansion of the gases extends between still wider limits; but, as liquidity is a state of transition from the solid to the aëriform condition, the equable dilatation of liquids has not so extensive a range. This change of bulk, corresponding to the variation of heat, is one of the most important of its effects, since it furnishes the means of measuring relative temperature by the thermometer and pyrometer. The rate of expansion of solids varies at their transition to liquidity, and that of liquidity is no longer equable near their change to an aëriform state. There are exceptions, however, to the general laws of expansion; some liquids have a maximum density corresponding to a certain temperature, and dilate whether that temperature be increased or diminished. For example—water expands whether it be heated above or cooled below 40°. The solidification of some liquids, and especially their crystallization, is always accompanied by an increase of bulk. Water dilates rapidly when converted into ice, and with a force sufficient to split the hardest substances. The formation of ice is therefore a powerful agent in the disintegration and decomposition of rocks, operating as one of the most efficient causes of local changes in the structure of the crust of the earth; of which we have experience in the tremendous éboulemens of mountains in Switzerland. But Professor W. Thomson has proved experimentally that it requires a lower temperature to freeze water under pressure than when free.
272The dilatation of substances by heat, and their contraction by cold, occasion such irregularities in the rate of clocks and watches as would render them unfit for astronomical or nautical purposes, were it not for a very beautiful application of the laws of unequal expansion. The oscillations of a pendulum are the same as if its whole mass were united in one dense particle, in a certain point of its length, called the centre of oscillation. If the distance of this point from the point by which the pendulum is suspended were invariable, the rate of the clock would be invariable also. The difficulty is to neutralize the effects of temperature, which is perpetually increasing or diminishing its length. Among many contrivances, Graham’s compensation pendulum is the most simple. He employed a glass tube containing mercury. When the tube expands from the effects of heat, the mercury expands much more; so that its surface rises a little more than the end of the pendulum is depressed, and the centre of oscillation remains stationary. Harrison invented a pendulum which consists of seven bars of steel and of brass, joined in the shape of a gridiron, in such a manner that, if by change of temperature the bars of brass raise the weight at the end of the pendulum, the bars of steel depress it as much. In general, only five bars are used; three being of steel, and two a mixture of silver and zinc. The effects of temperature are neutralized in chronometers upon the same principle; and to such perfection are they brought, that the loss or gain of one second in twenty-four hours for two days running would render one unfit for use. Accuracy in surveying depends upon the compensation rods employed in measuring bases. Thus, the laws of the unequal expansion of matter judiciously applied have an immediate influence upon our estimation of time; of the motions of bodies in the heavens, and of their fall upon the earth; on our determination of the figure of the globe, and on our system of weights and measures; on our commerce abroad, and the mensuration of our lands at home.
The expansion of the crystalline substances takes place under very different circumstances from the dilatation of such as are not crystallized. The latter become both longer and thicker by an accession of heat, whereas M. Mitscherlich has found that the former expand differently in different directions; and, in a particular instance, extension in one direction is accompanied by contraction in another: for example, Iceland spar is dilated 273in the direction of its axis of double refraction (N. 205), but at right angles to that axis it is contracted, which brings the crystal nearer to the form of the cube and diminishes its double refractive power. When heat is applied to crystals of sulphate of lime, the two optical axes (N. 207) gradually approach, and at last coincide; when the heat is increased, the axes open again, but in a direction at right angles to their former position. By experiment M. Senarmont has concluded, that in media constituted like crystals of the rhomboidal (N. 169) system the conducting power varies in such a manner, that, supposing a centre of heat to exist within them, and the medium to be indefinitely extended in all directions, the isothermal surfaces are concentric ellipsoids of revolution round the axes of symmetry, or at least surfaces differing but little from them. The internal structure of crystallized matter must be very peculiar thus to modify the expansive power of heat.
Heat applied to the surface of a fluid is propagated downwards very slowly, the warmer, and consequently lighter strata, always remaining at the top. This is the reason why the water at the bottom of lakes fed from Alpine chains is so cold; for the heat of the sun is transfused but a little way below the surface. When the heat is applied below a liquid, the particles continually rise as they become specifically lighter, and diffuse the heat through the mass, their place being perpetually supplied by those that are more dense. The power of conducting heat varies materially in different liquids. Mercury conducts twice as fast as an equal bulk of water, and therefore it appears to be very cold. A hot body diffuses its heat in the air by a double process: the air in contact with it becoming lighter ascends and scatters its heat by transmission, while at the same time another portion is discharged in straight lines by the radiating power of the surface. Hence a substance cools more rapidly in air than in vacuo, because in the latter case the process is carried on by radiation alone. It is probable that the earth having been originally of very high temperature has become cooler by radiation alone, the ethereal medium being too rare to carry off much heat by contact.
Heat is propagated with more or less rapidity through all bodies; air is the worst conductor, and consequently mitigates the severity of cold climates by preserving the heat imparted 274to the earth by the sun. On the contrary, dense bodies, especially metals, possess the power of conduction in the greatest degree, but the transmission requires time. If a bar of iron twenty inches long be heated at one extremity, the heat takes four minutes in passing to the other. The particle of the metal that is first heated communicates the heat to the second, and the second to the third: so that the temperature of the intermediate molecule at any instant is increased by the excess of the temperature of the first above its own, and diminished by the excess of its own temperature above that of the third. That however will not be the temperature indicated by the thermometer, because as soon as the particle is more heated than the surrounding atmosphere it loses its heat by radiation, in proportion to the excess of its actual temperature above that of the air. The velocity of the discharge is directly proportional to the temperature, and inversely as the length of the bar. As there are perpetual variations in the temperature of all terrestrial substances, and of the atmosphere, from the rotation of the earth, and its revolution round the sun, from combustion, friction, fermentation, electricity, and an infinity of other causes, the tendency to restore the equability of temperature by the transmission of heat must maintain all the particles of matter in a state of perpetual oscillation, which will be more or less rapid according to the conducting powers of the substances. From the motion of the heavenly bodies about their axes, and also round the sun, exposing them to perpetual changes of temperature, it may be inferred that similar causes will produce like effects in them too. The revolutions of the double stars show that they are not at rest; and although we are totally ignorant of the changes that may be going on in the nebulæ and millions of other remote bodies, it is hardly possible that they should be in absolute repose; so that, as far as our knowledge extends, motion is a law of the universe and the immediate cause of heat, as in the sunbeam so also in all terrestrial phenomena.
This is by no means hypothetical, but founded upon fact and experiment. Heat is produced by motion and is equivalent to it, for we measure heat by motion in the thermometer. The heat evolved by percussion is proportional to the force of the blow; by repeated blows iron becomes red hot; and the quantity of 275heat produced by friction, whether the matter be solid or fluid, is always in proportion to the force employed: in cold weather we rub our hands to make them warm, and the harder we rub the warmer they become. The warmth of the sea after a storm is in proportion to the force of the wind; and in Sir Humphry Davy’s experiment of melting ice by friction in the receiver of an air-pump kept at the freezing point, the heat which melted the ice was exactly proportional to the force of friction. This experiment proves the immateriality of heat, since the capacity of ice for heat is less than that of water. Thus mechanical action and heat are equivalent to one another. Mr. Joule of Manchester[13] has proved that the quantity of heat requisite to raise the temperature of a pound of water one degree of Fahrenheit’s thermometer, is equivalent to the mechanical force developed by the fall of a body weighing 772·69 pounds through the perpendicular height of one foot. This quantity is the mechanical equivalent of heat. Thus heat is motion, and it is measured by force. In fact, for every unit of force expended in friction or percussion, a definite quantity of heat is generated; and conversely, when work is performed by the consumption of heat, for each unit of force gained, a unit of heat disappears. For since heat is a dynamical force of mechanical effect, there must be an equivalent between mechanical work and heat as between cause and effect. (N. 222.)
Besides the temperature indicated by the thermometer, bodies absorb heat, and their capacity for heat is so various that very different quantities of heat are required to raise different substances to the same sensible temperature. It is evident, therefore, that much of the heat is absorbed and becomes insensible to the thermometer. That portion of heat requisite to raise a body to a given temperature is its specific heat, but the latent or absorbed heat is an expansive force or energy, which, acting upon the ether surrounding the ultimate particles of bodies, changes them from solid to liquid, and from liquid to vapour or gas. According to the law of absorption, the transfer of heat from a warm body to one that is cold is a 276mere transfer of force, in which the force of compression is exactly proportional to the force of expansion. Ice remains at the temperature of 32° Fahrenheit till it has absorbed 140° of heat, and then it melts, but without raising the temperature of the water above 32°. On the contrary, when a liquid is converted into a solid, a quantity of heat leaves it without any diminution of temperature. Thus water at 32° must part with 140° of heat before it freezes. The slowness with which water freezes or ice thaws, is a consequence of the time required for the ethereal atmospheres round the particles of the water to contract or expand with a force equivalent to 140° of heat. A considerable degree of cold is felt during a thaw, because the ice in its transition from a solid to a liquid state absorbs sensible heat from the atmosphere and surrounding objects. The heat absorbed and evolved by the rarefaction and condensation of air is exactly proportional to the force evolved and absorbed in these operations. In fact, the changes of temperature produced by these rarefactions and condensations of air show that the heat of elastic fluids is the mechanical force possessed by them; and since the temperature of a gas determines its elastic force, it follows that the elastic force or pressure must be the effect of the motion of the constituent particles in any gas. Sir Humphry Davy, who first demonstrated the immateriality of heat, assumed the hypothesis that the motion we call heat is a rotation or vibration among the particles of the fluid, which, according to Mr. Joule, agrees perfectly with the observed phenomena, but he prefers the more simple view of Mr. Herapath, that the elastic force or pressure is due to the impact of the particles against any surface presented to them. Absorbed or latent heat may be regarded as a quiescent energy ready to be restored to the form of sensible heat when called forth: its vibrations as heat are extinguished for the time by being transferred to the internal expansive force, and are restored by compression. The absorbed heat of air and all elastic fluids may be forced out by sudden compression like squeezing water out of a sponge. The quantity of heat brought into action in this way is well illustrated by the experiment of igniting tinder by the sudden compression of air by a piston thrust into a cylinder closed at one end. The development of heat on a stupendous scale is exhibited in lightning: it is proportional to the square of the quantity 277of electricity discharged, and is due to its excessive velocity and the violent compression of the air in its transit through the atmosphere. Prodigious quantities of heat are constantly absorbed or disengaged by the changes to which substances are liable in passing from the solid to the liquid and from the liquid to the gaseous form and the contrary, causing endless vicissitudes of temperature over the globe, and endless expansions and contractions, which are correlative terms for heat and cold, while radiation of heat is merely a transfer of motion from the particles on the surface of bodies to the adjacent particles of the atmosphere.
By the continual application of heat, that is of the expansive force, liquids are converted into steam or vapour, which is invisible and highly elastic. Under the mean pressure of the atmosphere, that is when the barometer stands at 30 inches, water in a boiler absorbs heat continually till it attains the temperature of the boiling point, which is 212° Fahrenheit. After that it ceases to show any increase of sensible heat; but when it has absorbed an additional 1000° of heat or expansive energy, that energy converts it into steam, and a condensing force equivalent to 1000° of heat reduces it again to water. Water boils at different temperatures under different degrees of pressure. It boils at a lower temperature on the top of a mountain than on the plain below, because the weight of the atmosphere is less at the higher station. There is no limit to the temperature to which water might be raised: it might even be made red hot, could a vessel be found strong enough to resist the pressure, for the intensity of the expansive force prevented from having effect by the extreme pressure of the boiler would be converted into sensible heat which might eventually render the water red hot. Thus, since the force of steam is in proportion to the temperature at which the water boils, or to the pressure, it is under control, and, perhaps with the exception of electricity, it is the greatest power that has been made subservient to the wants of man.
It is found that the absolute quantity of heat consumed in the process of converting water into steam is the same at whatever temperature water may boil, but that the absolute heat of the steam is greater exactly in proportion as its sensible heat is less. Thus, steam raised at 212° Fahrenheit under the mean 278pressure of the atmosphere, and steam raised at 180° under half the pressure, contain the same quantity of heat, with this difference, that the one has more absorbed heat and less sensible heat than the other. It is evident that, as the same quantity of heat is requisite for converting a given weight of water into steam, at whatever temperature or under whatever pressure the water may be boiled, therefore, in the steam engine, equal weights of steam at a high pressure and a low pressure are produced by the same quantity of fuel; and whatever the pressure of the steam may be, the consumption of fuel is proportional to the quantity of water converted into vapour. Steam of whatever tension expands on being set free, but the expansion of high pressure steam at the expense of its sensible heat is so great, that the hand may be plunged into it without injury the instant it issues from the orifice of a boiler. The steam becomes hotter by friction in issuing through the orifice which maintains it in its dry form, for there is no doubt that high-pressure steam is dry.
The elasticity or tension of steam, like that of common air, varies inversely as its volume—that is, when the space it occupies is doubled, its elastic force is reduced to one half. The expansion of steam is indefinite; the smallest quantity of water expanded into vapour will occupy many millions of cubic feet; a wonderful illustration of the minuteness of the ultimate particles of matter.
The force of steam, tremendous as the lightning itself when uncontrolled, is merely the result of chemical affinity: it is the chemical attraction between the particles of carbon, of coal or wood, and the oxygen of the atmosphere. Mr. Joule has ascertained that a pound of the best coal when burnt gives sufficient heat to raise the temperature of 8086 pounds of water one degree of the Centigrade thermometer, whence it has been computed by M. Helmholtz that the chemical force arising from the combustion of that pound of coal is capable of lifting a body of one hundred pounds weight to the height of twenty miles. That is the work performed by the heat arising from the combustion of a pound of coal. In all cases where work is produced by heat, a quantity of heat proportional to the work done is expended; and conversely, by the expenditure of a like quantity of work, the same amount of heat may be produced. The equivalence of heat and work is a law of nature. The mechanical force exerted by 279the steam engine for example is exactly proportional to the consumption of heat, nor more nor less; if we could produce a greater quantity than its equivalent we should have perpetual motion, which is impossible. Mechanical engines generate no force. We cannot create force; we can only avail ourselves of the inexhaustible stores of nature, the lightning, fire, water, wind, chemical action, &c. The quantity of mechanical power in nature is ever the same; it is never increased, it is never diminished, throughout the whole circuit of natural powers. The conservation of force is as permanent and unchangeable as matter. It may be dormant for a time, but it ever exists. We are unconscious of the enormous dynamic power that is either active or latent throughout the globe, because we do not attend to it. By the ebb and flow of the tide alone a power is exerted by which 25,000 cubic miles of water is moved over a quarter of the globe every twelve hours; and Professor W. Thomson has computed, by means of Pouillet’s data of solar radiation and Mr. Joule’s mechanical equivalent of heat, that the mechanical value of the whole energy active and potential of the disturbances kept up in the ethereal medium by the vibrations of the solar light within a cubic mile of our atmosphere is equal to 12,050 times the unit of mechanical force, that is to say, 12,050 times the force that would raise a pound of matter to the height of one foot, whence some idea may be formed of the vast amount of force exerted by the sun’s light within the limits of the whole terrestrial atmosphere. (N. 223.)
The dynamic energy of the undulations of the solar light gives the leaves of plants the power of decomposing carbonic acid, and of separating the particles of carbon and hydrogen from the oxygen for which they have so strong an affinity. In this operation the undulations of the sunbeam are extinguished as light and heat, and Professor W. Thomson has proved that the quantity of these undulations thus extinguished is precisely equal to the potential or quiescent energy thus created, and that precisely that very quantity of light and heat is restored when the plants are burned, whatever state they may be in; and that thus, as Mr. George Stephenson[14] has truly and beautifully observed, our coal fires 280and gas lamps restore to our use the light and heat of the sun of the early geological epochs which have rested as dormant powers under the seas and mountains for unnumbered ages. The sun is therefore the source of the mechanical energy of all the heat and motion of inanimate things, of all the motions of the heat and light of fires and artificial flames, and of the heat of all living creatures. For animal heat, and weights raised or resistance overcome, are mechanical effects of the chemical combination of food with oxygen; and food is either directly or indirectly vegetable, consequently dependent upon the sun.
Professor Helmholtz of Bonn has put in a strong point of view the enormous store of force possessed by our system by comparing it with its equivalent of heat. The force with which the earth moves in its orbit is such, that if brought to rest by a sudden shock, a quantity of heat would be generated by the blow equal to that produced by the combustion of fourteen such earths of solid coal; and supposing the capacity of the earth for heat as low as that of water, the globe would be heated to 11,200° Cent. It would be quite fused and for the most part reduced to vapour. If it should fall to the sun, which it would certainly do, the quantity of heat developed by the shock would be four hundred times as great.
The application of heat to the various branches of the mechanical and chemical arts has within the present century effected a greater change in the condition of man than had been accomplished in any equal period of his existence. Armed by the expansion and condensation of fluids with a power equal to that of the lightning itself, conquering time and space, he flies over plains, and travels on paths cut by human industry even through mountains with a velocity and smoothness more like planetary than terrestrial motion; he crosses the deep in opposition to wind and tide; by releasing the strain on the cable, he rides at anchor fearless of the storm; he makes the lightning his messenger; and like a magician he raises from the gloomy abyss of the mine the sunbeam of former ages to dispel the midnight darkness.
The principal phenomena of heat may be illustrated by a comparison with those of sound. Their excitation is not only similar but identical, as in friction and percussion; they are both communicated by contact and radiation; and Dr. Young observes that the effect of radiant heat in raising the temperature of a 281body upon which it falls, resembles the sympathetic agitation of a string when the sound of another string which is in unison with it is transmitted through the air. Light, heat, sound, and the waves of fluids are all subject to the same laws; their undulatory theories are perfectly similar: hence the interference of two hot rays must produce cold, that is, they must extinguish one another: darkness results from the interference of two undulations of light, silence ensues from the interference of two undulations of sound, and still water or no tide is the consequence of the interference of two tides. The propagation of sound, however, requires a much denser medium than that of light and heat; its intensity diminishes as the rarity of the air increases: so that, at a very small height above the surface of the earth, the noise of the tempest ceases, and the thunder is heard no more in those boundless regions where the heavenly bodies accomplish their periods in eternal and sublime silence.
A consciousness of the fallacy of our senses is one of the most important consequences of the study of nature. This study teaches us that no object is seen by us in its true place, owing to aberration; that the colours of substances are solely the effects of the action of matter upon light; and that light itself as well as heat and sound are not real beings, but mere motions communicated to our perceptions by the nerves. The human frame may therefore be regarded as an elastic system, the different parts of which are capable of receiving the tremors of elastic media, and of vibrating in unison with any number of superimposed undulations, all of which have their perfect and independent effect. Here our knowledge ends: the mysterious influence of matter on mind will in all probability be for ever hid from man.
Common or Static Electricity, or Electricity of Tension—A Dual Power—Methods of exciting it—Attraction and Repulsion—Conduction—Electrics and Non-electrics—Induction—Dielectrics—Tension—Law of the Electric Force—Distribution—Laws of Distribution—Heat of Electricity—Electrical Light and its Spectrum—Velocity—Atmospheric Electricity—Its cause—Electric Clouds—Violent effects of Lightning—Back Stroke—Electric Glow—Phosphorescence.
Electricity is a dual power which gives no visible sign of its existence when in equilibrio, but when elicited forces are developed capable of producing the most sudden, violent, and destructive effects in some cases, while in others their action, though generally less energetic, is of indefinite and uninterrupted continuance. These modifications of the electric forces, incidentally depending upon the manner in which they are excited, present phenomena of great diversity, but yet so connected as to justify the conclusion that they originate in a common principle. The hypothesis of electricity being a fluid is untenable in the present advanced state of the science; we only know that it is a force whose action is twofold; that bodies in one electric state attract, and in another repel each other; in the former the electricity is said to be positive, in the latter negative; and thus regarding it as a force, its modes of action come under the laws of mechanics and mathematical analysis.
Electricity may be called into activity by the friction of heterogeneous substances, as in the common electrifying machine, by mechanical power, heat, chemical action, and the influence of magnetism. We are totally ignorant why it is roused from its neutral state by these means, or of the manner of its existence in bodies; but when excited it seems to produce a molecular polarity or chemical change in the ultimate particles of matter.
The science is divided into various branches, of which static or common electricity comes first under consideration, including that of the atmosphere. Substances in a neutral state neither attract nor repel. There is a numerous class called electrics in 283which the electric equilibrium is destroyed by friction; then the positive and negative electricities are called into action or separated; the positive is impelled in one direction, and the negative in another. Electricities of the same kind repel, whereas those of different kinds attract each other. The attractive power is exactly equal to the repulsive power at equal distances, and when not opposed they coalesce with great rapidity and violence, producing the electric flash, explosion, and shock; then the equilibrium is restored. One kind of electricity cannot be evolved without the evolution of an equal quantity of the opposite kind. Thus when a glass rod is rubbed with a piece of silk, as much positive electricity is elicited in the glass as there is negative in the silk. The kind of electricity depends more upon the mechanical condition than on the nature of the surface; for when two plates of glass, one polished and the other rough, are rubbed against each other, the polished surface acquires positive and the rough negative electricity. The manner in which friction is performed also alters the kind of electricity. Equal lengths of black and white ribbon applied longitudinally to one another, and drawn between the finger and thumb so as to rub their surfaces together, become electric. When separated the white ribbon is found to have acquired positive electricity, and the black negative; but if the whole length of the black ribbon be drawn across the breadth of the white, the black will be positively and the white negatively electric when separated. The friction of the rubber on the glass plate of the electrifying machine produces abundance of static electricity. The friction of the steam on the valve of an insulated locomotive steam-engine produces seven times the quantity of electricity that an electrifying machine would do with a plate three feet in diameter, worked at the rate of 70 revolutions in a minute. Pressure is a source of electricity which M. Becquerel has found to be common to all bodies; but it is necessary to separate them to prevent the reunion of the electricities. When two substances of any kind whatever are insulated and pressed together they assume different electric states, but they only show contrary electricities when one of them is a good conductor. When both are good conductors they must be separated with extreme rapidity to prevent a return to equilibrium. When the separation is very sudden the tension of the two electricities may be 284great enough to produce light. M. Becquerel attributes the light produced by the collision of icebergs to this cause. Iceland spar is made electric by the smallest pressure between the finger and the thumb, and retains it for a long time. All these circumstances are modified by the temperature of the substances, the state of their surfaces and that of the atmosphere. Several crystalline bodies become electric when heated, especially tourmaline, one end of which acquires positive, and the other negative electricity, while the intermediate part is neutral. If the tourmaline be broken through the middle, each fragment is found to possess positive electricity at one end and negative at the other. Electricity is evolved by substances passing from a liquid to a solid state, and by chemical action during the production and condensation of vapour, which is a great source of atmospheric electricity. In short, it may be generally stated, that when any cause whatever tends to destroy molecular attraction there is a development of electricity; if, however, the substances be not immediately separated, there will be an instantaneous restoration of equilibrium.
Electricity may be transferred from one body to another in the same manner as heat is communicated, and like it too the body loses by the transmission.
Although no substance is altogether impervious to electricity, nor is there any that does not offer some resistance to its passage, yet it moves with more facility through a certain class of substances called conductors, such as metals, water, the human body, &c., than through atmospheric air, glass, silk, &c., which are therefore called non-conductors. The conducting power is affected both by temperature and moisture. The terrestrial globe is a conductor on account of its moisture, though dry earth is not. Though metals are the best conductors of electricity, it affects their molecular structure, for the heat which accompanies its passage acts as a transverse expansive force, which increases their breadth by diminishing their length, as may be seen by passing electricity through a platinum wire sufficiently thick to resist fusion. Through air the force is disruptive on account of its non-conducting quality, and it seems to act chemically on the oxygen, producing the substance known as ozone during its passage through the atmosphere. If a conductor be good and of sufficient size the electricity passes imperceptibly 285but it is shivered to pieces in an instant if it be a bad conductor or too small to carry off the charge. In that case the physical change is generally a separation of the particles, or expansion from the heat, as in trees, where it turns the moisture into steam, but all these effects are in proportion to the obstacles opposed to the freedom of its course.
Bodies surrounded by non-conductors are said to be insulated, because when charged the electricity cannot escape. When that is not the case, the electricity is conveyed to the earth: consequently it is impossible to accumulate electricity in a conducting substance that is not insulated. There are a great many substances called non-electrics in which electricity is not sensibly developed by friction unless they be insulated, because it is carried off by their conducting power as soon as elicited. Metals, for example, which are said to be non-electrics can be excited, but being conductors they cannot retain this state if in communication with the earth. It is probable that no bodies exist which are either perfect non-electrics or perfect non-conductors. But it is evident that electrics must be non-conductors to a certain degree, otherwise they could not retain their electric state.
A body charged with electricity, although perfectly insulated, so that all escape of electricity is prevented, tends to produce an electric state of the opposite kind in all bodies in its vicinity. Positive electricity tends to produce negative electricity in a body near to it, and vice versâ, the effect being greater as the distance diminishes. This power which electricity possesses of causing an opposite electrical state in its vicinity is called induction. A Leyden jar, for example, or glass jar coated half way up both outside and in with tin foil, when charged with positive electricity, immediately induces negative electricity on the tin foil outside. Notwithstanding their strong mutual attraction they are prevented from coalescing by the glass, which is a non-conductor; but if the tin inside and out be connected by a conducting wire they instantly unite. When a body in either electric state is presented to a neutral one, its tendency in consequence of the law of induction is to disturb the condition of the neutral body by inducing electricity contrary to its own in the adjacent side, and therefore an electrical state similar to its own in the remote part. Hence the neutrality of the second body is destroyed by the action of the first, and the adjacent parts of the 286two, having now opposite electricities, will attract each other. The attraction between electrified and unelectrified substances is a consequence of the altered state of their molecules. Induction depends upon the facility with which the equilibrium of the neutral body can be overcome, a facility which is proportional to its conducting power. Consequently the attraction exerted by an electrified substance upon another substance previously neutral will be much more energetic if the latter be a conductor than if it be a non-conductor.
It is clear that one body cannot act upon another at a distance without some means of communication. Dr. Faraday has proved that the intervening non-conducting substance or dielectric has a great influence upon induction. Thus the inductive force is greater when sulphur is interposed between the two bodies than when shellac is the dielectric, and greater when shellac is the dielectric than glass, &c. Professor Matteucci has proved by the following experiment that the intervening substance is itself polarized by induction. A number of plates of mica in contact were placed between two plates of metal, one of which was electrified, so that the whole was charged like a Leyden jar. On separating the plates with insulating handles, each plate of mica was electrified; one side of it was positive and the other negative, showing decidedly a polarization by induction throughout the whole intervening non-conducting substance; and thus, although the interposed substance or dielectric is incapable of conducting the electrical force from one body to the other, it becomes by induction capable of transmitting it. In the atmosphere induction is transmitted by that of the intervening strata of air. It is true that induction takes place through the most perfect vacuum we can make, but there always remains some highly elastic air; and even if air could be altogether excluded, the ethereal medium cannot, and it must be capable of induction, since, however attenuated, it must consist of material atoms, otherwise it would be a nonentity.
The law of electrical attraction and repulsion has been determined by suspending a needle of gum-lac horizontally by a silk fibre, the needle carrying at one end a piece of electrified gold leaf. A globe in the same or opposite electrical state when presented to the gold leaf will repel or attract it, and will therefore cause the needle to vibrate more or less rapidly according 287to the distance of the globe. A comparison of the number of oscillations performed in a given time at different distances will determine the law of the variation of the electrical intensity, in the same manner that the force of gravitation is measured by the oscillations of the pendulum. Coulomb invented an instrument which balances the forces in question by the force of the torsion of a thread, which consequently measures the intensity; and Sir William Snow Harris has constructed an instrument with which he has measured the intensity of the electrical force in terms of the weight requisite to balance it. By these methods it has been found that the intensity of electrical attraction and repulsion varies inversely as the square of the distance. However, the law of repulsive force is liable to great disturbances from inductive action, which Sir William Snow Harris has found to exist not only between a charged and neutral body, but also between bodies similarly charged; and that, in the latter case, the inductive process may be indefinitely modified by the various circumstances of the quantity and intensity of the electricity and the distance between the charged bodies.
The quantity of electricity bodies are capable of receiving does not follow the proportion of their bulk, but depends principally upon the form and extent of their surface. It appears from the experiments of Sir W. S. Harris that a given quantity of electricity, divided between two perfectly equal and similar bodies, exerts upon external bodies only one fourth of the attractive force apparent when disposed upon one of them; and if it be distributed among three equal and similar bodies, the force is one ninth of that apparent when it is disposed on one of them. Hence, if the quantity of electricity be the same, the force varies inversely as the square of the surface on which it is disposed; and if the surface be the same, the force varies directly as the square of the quantity of electricity. These laws however do not hold when the form of the surface is changed. A given quantity of electricity disposed on a given surface has the greatest intensity when the surface has a circular form, and the least intensity when the surface is expanded into an indefinite straight line. The decrease of intensity seems to arise from some peculiar arrangement of the electricity depending on the extension of the surface. It is 288quite independent of the extent of the edge, the area being the same; for Sir W. S. Harris found that the electrical intensity of a charged sphere is the same with that of a plane circular area of the same superficial extent, and that of a charged cylinder the same as if it were cut open and expanded into a plane surface.
The same able electrician has shown that the attractive force between an electrified and a neutral uninsulated body is the same whatever be the forms of their unopposed parts. Thus two hemispheres attract each other with precisely the same force as if they were spheres; and as the force is as the number of attracting points in operation directly, and as the squares of the respective distances inversely, it follows that the attraction between a mere ring and a circular area is no greater than that between two similar rings, and the force between a sphere and an opposed spherical segment of the same curvature is no greater than that of two similar segments, each equal to the given segment.
Electricity may be accumulated to a great extent in insulated bodies, and so long as it is quiescent it occasions no sensible change in their properties. When restrained by the non-conducting power of the atmosphere, its tension or the pressure it exerts is proportional to the coercive force of the air. If the pressure be less than the coercive force, the electricity is retained; but the instant it exceeds that force in any one point it escapes, and that more readily when the air is attenuated or saturated with moisture, for the resistance of the air is proportional to the square of its density, but the inductive action of electricity on distant bodies is independent of atmospheric pressure. The power of retaining electricity depends also on the shape of the charged body. It is most easily retained by a sphere, next to that by a spheroid, but it readily escapes from a point, and a pointed object receives it with most facility.
The heat produced by the electric shock is proportional to the square of the quantity of electricity discharged, and is so intense that it fuses metals and volatilizes substances, but its intensity is not felt to its full extent on account of the shortness of its duration. It is only accompanied by light when the electricity is obstructed in its passage through substance.
Electrical light when analysed by a prism differs very much 289from solar light. Fraunhofer found that, instead of the fixed dark lines, the spectrum of an electric spark is crossed by numerous bright lines; and Professor Wheatstone has observed that the number and position of the lines differ with the metal from which the spark is taken, and believes the spark itself results from the ignition and volatilization of the matter of the conductor.
According to the experiments of Sir Humphry Davy, the density of the air has an influence on the colour. He passed the electric spark through a vacuum over mercury, which from green became successively sea-green, blue, and purple, on admitting different quantities of air. When the vacuum was made over a fusible alloy of tin and bismuth, the spark was yellowish and extremely pale. Sir Humphry thence concluded that electrical light principally depends upon some properties belonging to the ponderable matter through which it passes, and that space is capable of exhibiting luminous appearances, though it does not contain an appreciable quantity of matter. He thought that the superficial particles of bodies which form vapour, when detached by the repulsive power of heat, might be equally separated by the electric forces, and produce luminous appearances in vacuo by the destruction of their opposite electric states.
The velocity of electricity is so great that the most rapid motion which can be produced by art appears to be actual rest when compared with it. A wheel revolving with celerity sufficient to render its spokes invisible, when illuminated by a flash of lightning, is seen for an instant with all its spokes distinct, as if it were in a state of absolute repose; because, however rapid the rotation may be, the light has come and already ceased before the wheel has had time to turn through a sensible space. This beautiful experiment is due to Professor Wheatstone, as well as the following variation of it, which is not less striking: If a circular piece of pasteboard be divided into three sectors, one of which is painted blue, another yellow, and a third red, it will appear to be white when revolving quickly, because of the rapidity with which the impressions of the colours succeed each other on the retina. But, the instant it is illuminated by an electric spark, it seems to stand still, and each colour is as distinct as if it were at rest. This transcendent speed of electricity has 290been ingeniously measured, as follows, by Professor Wheatstone, who has ascertained that it much surpasses the velocity of light.
In the horizontal diameter of a small disc, fixed on the wall of a darkened room, are disposed six small brass balls, well insulated from each other. An insulated copper wire, half a mile long, is disjointed in its middle, and also near its two extremities; the six ends thus obtained are connected with the six-balls on the disc. When an electric discharge is sent through the wire by connecting its two extremities, one with the positive, and the other with the negative coating of a Leyden jar, three sparks are seen on the disc, apparently at the same instant. At the distance of about ten feet a small revolving mirror is placed so as to reflect these three sparks during its revolution. From the extreme velocity of the electricity, it is clear that, if the three sparks be simultaneous, they will be reflected, and will vanish before the mirror has sensibly changed its position, however rapid its rotation may be, and they will be seen in a straight line. But if the three sparks be not simultaneously transmitted to the disc—if one, for example, be later than the other two—the mirror will have time to revolve through an indefinitely small arc in the interval between the reflection of the two sparks and that of the single one. However, the only indication of this small motion of the mirror will be, that the single spark will not be reflected in the same straight line with the other two, but a little above or below it, for the reflection of all three will still be apparently simultaneous, the time intervening being much too short to be appreciated.
Since the number of revolutions which the revolving mirror makes in a second is known, and the angular deviation of the reflection of the single spark from the reflection of the other two can be measured, the time elapsed between their consecutive reflections can be ascertained. And, as the length of that part of the wire through which the electricity has passed is given, its velocity may be found.
The number of pulses in a second, requisite to produce a musical note of any pitch, are known; hence the number of revolutions accomplished by the mirror in a given time may be determined from the musical note produced by a tooth or peg, in its axis of 291rotation, striking against a card, or from the notes of a siren attached to the axis. It was thus that Professor Wheatstone found the mirror which he employed in his experiments made 800 revolutions in a second; and, as the angular velocity of the reflected image in a revolving mirror is double that of the mirror itself, an angular deviation of one degree in the appearance of the two sparks would indicate an interval of the 576,000th of a second; the deviation of half a degree would, therefore, indicate more than the millionth of a second. The use of sound as a measure of velocity is a happy illustration of the connexion of the physical sciences.
The earth possesses a powerful electrical tension, and the atmosphere when clear is almost always positively electric. Its electricity is stronger in winter than in summer, during the day than in the night. The intensity increases for two or three hours from the time of sunrise, comes to a maximum between seven and eight, then decreases towards the middle of the day, arrives at its minimum between one and two, and again augments as the sun declines till about the time of sunset, after which it diminishes and continues feeble during the night. The mere condensation of vapour is a source of atmospheric electricity; but although it is also produced by the vapour that rises from the surface of the earth, it is not under all circumstances. M. Pouillet found that electricity is only developed when accompanied by chemical action: for example, when the water whence the vapour proceeds contains lime, chalk, or any solid alkali, negative electricity is produced; and when it holds in solution either gas, acid, or some of the salts, the vapour is positively electric. Besides, the contact of earth with salt and fresh water generates positive electricity, and the contact of fresh and salt currents of water negative, so that the ocean must afford a great supply to the atmosphere; hence thunderstorms are most frequent near the coasts: but as electricity of one kind or another is developed whenever the molecules of matter are deranged from their natural state of equilibrium, there must be many partial variations in the electric state of the air. When the invisible vapour rises charged with electricity into the cold regions of the atmosphere, it is condensed into cloud, in which the tension is increased because the electricity is confined to a smaller space; and if the condensation 292be sufficient to produce drops of rain, they carry the electricity to the ground, so that in general a shower is a conductor between the clouds and the earth. When two clouds charged with opposite kinds, but of equal tension, approach within a certain distance, the intensity increases on the sides of the clouds that are nearest to one another; and when the tension is great enough to overcome the coercive pressure of the atmosphere, a discharge takes place which causes a flash of lightning, the stroke being given either by the cloud or the rain. The actual quantity of electricity in any part of a cloud is extremely small. The intensity of the flash arises from the great extent of surface over which it is spread, so that clouds may be compared to enormous Leyden jars thinly coated with electricity, which only acquires its intensity by its instantaneous condensation. The rapid and irregular motions of thunder clouds are probably more owing to strong electrical attractions and repulsions among themselves than to currents of air, though both are no doubt concerned in these hostile movements. The atmosphere becomes intensely electric on the approach of rain, hail, snow, sleet, and wind; but it varies afterwards, and the transitions are very rapid on the approach of a thunderstorm.
Since air is a non-conductor, it does not convey the electricity from the clouds to the earth, but it acquires from them an opposite kind, and when the tension is very great the force of the electricity becomes irresistible, and an interchange takes place between the clouds and the earth; but so rapid is the motion of lightning, that it is difficult to ascertain whether it goes from the clouds to the earth or shoots upwards from the earth to the clouds, though there can be no doubt that it does both. In a storm that occurred at Manchester in June 1835, the lightning was observed to issue from various points of a road, attended by explosions as if pistols had been fired out of the ground, and a man seems to have been killed by one of these explosions taking place under his foot. M. Gay Lussac ascertained that a flash of lightning sometimes darts more than three miles in a straight line. A person may be killed by lightning, although the explosion takes place at a distance of twenty miles, by what is called the back stroke. Suppose that the two extremities of a highly charged cloud hang down towards the earth, they will repel the 293electricity from the earth’s surface if it be of the same kind with their own, and will attract the other kind; and if a discharge should suddenly take place at one end of the cloud, the equilibrium will be instantly restored by a flash at that point of the earth which is under the other. Though the back stroke is often sufficiently powerful to destroy life, it is never so terrible in its effects as the direct stroke, which is often of inconceivable intensity. Instances have occurred when large masses of iron and stone, and even many feet of a stone wall, have been carried to a considerable distance by a stroke of lightning. Rocks and the tops of mountains often bear the marks of fusion from its intense heat; and occasionally vitreous tubes descending many feet into banks of sand mark its path. Dr. Fiedler exhibited several of these fulgorites in London of considerable length, which had been dug out of the sandy plains of Silesia and Eastern Prussia. One found at Paderborn was forty feet long. Their ramifications generally terminate in pools or springs of water below the sand, which are supposed to determine the course of the lightning. No doubt the soil and substrata must influence its direction, since it is found by experience that places which have been once struck by lightning are often struck again. An insulated conductor on the approach of a storm gives out such quantities of sparks that it is dangerous to approach it, as was fatally experienced by Professor Richman at Petersburg, who was struck dead by a globe of fire from the extremity of a conductor, while making experiments on atmospheric electricity. Copper conductors afford the best protection, especially if they expose a broad surface, since electricity is conveyed along the surface of bodies. There is no instance of an electric cloud of high tension being dispelled by a conductor, yet those invented by Sir William Snow Harris, and universally employed in the navy, afford a complete protection in the most imminent danger. The Shannon, a 50-gun frigate, commanded by the brave and lamented Sir William Peel, was enveloped in a thunder-storm when about 90 miles to the north-west of Java. It began at fifty minutes past four in the afternoon; the ship was driven before the storm, in a high sea, amid streams of vivid lightning, deafening thunder, hail, and rain. At five o’clock an immense ball of fire covered the maintopgallant mast, ran up the royal pole, and exploded in the air with a terrific concussion, covering all the surrounding space 294with sparks of electric light, which were driven rapidly to leeward by the wind. Fifteen minutes later an immense mass of lightning struck the mainmast, attended by a violent gust of wind; and another heavy discharge fell on it a quarter of an hour afterwards. From that time till six o’clock the ship was continually encompassed by sharp forked lightning, accompanied by incessant peals of thunder. Though actually enveloped in electricity, and struck three times, neither the hull nor the rigging sustained the slightest injury.
When the air is rarefied by heat, its coercive power is diminished, so that the electricity escapes from the clouds in those lambent diffuse flashes without thunder so frequent in warm summer evenings; and when the atmosphere is highly charged with electricity, it not unfrequently happens that electric light, in the form of a star, is seen on the topmasts and yard-arms of ships. In 1831 the French officers at Algiers were surprised to see brushes of light on the heads of their comrades, and at the points of their fingers when they held up their hands. This phenomenon was well known to the ancients, who reckoned it a lucky omen.
Many substances, in decaying, emit light, which is attributed to electricity, such as fish and rotten wood. Oyster-shells, and a variety of minerals, become phosphorescent at certain temperatures when exposed to electric shocks or friction: indeed, most of the causes which disturb molecular equilibrium give rise to phosphoric phenomena. The minerals possessing this property are generally coloured or imperfectly transparent; and, though the colour of this light varies in different substances, it has no fixed relation to the colour of the mineral. An intense heat entirely destroys this property, and the phosphorescent light developed by heat has no connexion with light produced by friction; for Sir David Brewster observed that bodies deprived of the faculty of emitting the one are still capable of giving out the other. Among the bodies which generally become phosphorescent when exposed to heat, there are some specimens which do not possess this property; wherefore phosphorescence cannot be regarded as an essential character of the minerals possessing it. Sulphuret of calcium, known as Canton’s phosphorus, and the sulphuret of barium, or Bologna stone, possess the phosphorescent property in an eminent degree.
Multitudes of fish are endowed with the power of emitting 295light at pleasure, no doubt to enable them to pursue their prey at depths where the sunbeams cannot penetrate. Flashes of light are frequently seen to dart along a shoal of herrings or pilchards; and the Medusa tribes are noted for their phosphorescent brilliancy, many of which are extremely small, and so numerous as to make the wake of a vessel look like a stream of silver. Nevertheless, the luminous appearance which is frequently observed in the sea during the summer months cannot always be attributed to marine animalculæ, as the following narrative will show:—
Captain Bonnycastle, coming up the Gulf of St. Lawrence on the 7th of September, 1826, was roused by the mate of the vessel in great alarm from an unusual appearance. It was a starlight night, when suddenly the sky became overcast in the direction of the high land, and an instantaneous and intensely vivid light, resembling the aurora, shot out of the hitherto gloomy and dark sea on the lee bow, which was so brilliant that it lighted everything distinctly even to the mast-head. The light spread over the whole sea between the two shores, and the waves, which before had been tranquil, now began to be agitated. Captain Bonnycastle describes the scene as that of a blazing sheet of awful and most brilliant light. A long and vivid line of light, superior in brightness to the parts of the sea not immediately near the vessel, showed the base of the high, frowning, and dark land abreast; the sky became lowering and more intensely obscure. Long tortuous lines of light showed immense numbers of very large fish darting about as if in consternation. The sprit-sail yard and mizen-boom were lighted by the glare, as if gaslights had been burning directly below them; and until just before daybreak, at four o’clock, the most minute objects were distinctly visible. Day broke very slowly, and the sun rose of a fiery and threatening aspect. Rain followed. Captain Bonnycastle caused a bucket of this fiery water to be drawn up; it was one mass of light when stirred by the hand, and not in sparks as usual, but in actual coruscations. A portion of the water preserved its luminosity for seven nights. On the third night, the scintillations of the sea reappeared; the sun went down very singularly, exhibiting in its descent a double sun; and, when only a few degrees high, its spherical figure changed into that of a long cylinder, which reached the 296horizon. In the night the sea became nearly as luminous as before, but on the fifth night the appearance entirely ceased. Captain Bonnycastle did not think it proceeded from animalculæ, but imagined it might be some compound of phosphorus, suddenly evolved and disposed over the surface of the sea. It had probably been that peculiar form of electricity known as the glow discharge, of which the author once saw a very remarkable instance.
M. E. Becquerel assures us that almost all substances are phosphorescent after being exposed to the sun if instantly withdrawn into darkness, and that it depends upon the arrangement of the particles and not upon chemical action. The salts of uranium give the same kind of phosphorescent light as that produced by the violet rays of the solar spectrum. A solution of the bisulphate of quinine emits a yellow phosphorescent light, whereas the fluorescent light of that liquid is blue. The colours of these two kinds of light are generally complementary to one another.
Phosphorescence is probably more or less concerned in some, at least, of a series of very curious experiments made by M. Niepcé de Saint-Victor, on what he calls the saturation of substances with light. It has long been known that, if a person in an intensely dark room should expose his arm to the sun through a hole in a window-shutter, it will shine on being drawn into the darkness. Now, M. de Saint-Victor found that if an engraving be exposed for a certain time to the sun, and instantly brought into darkness, it will make a photographic impression on a collodion or argentine surface, and that anything written or drawn with tartaric acid, or a solution of the salts of uranium, in large characters, is reproduced even at a small distance from a sensitive surface. It may be presumed that the light communicates its vibrations to the surfaces exposed to it with sufficient force to enable them to disturb the unstable equilibrium of such sensitive substances as collodion or the argentine salts. M. de Saint-Victor has shown that tartaric acid, which is readily impressed by sunlight, is neither fluorescent nor phosphorescent, whence he concludes that his experiments are independent of both of these modes of action. Uranium appears to have very peculiar properties: its salts are strongly luminous when exposed to the sun; they are very fluorescent; and the crystallized azitote of uranium becomes phosphorescent by percussion.
Voltaic Electricity—The Voltaic Battery—Intensity—Quantity—Static Electricity, and Electricity in Motion—Luminous Effects—Mr. Grove on the Electric Arc and Light—Decomposition of Water—Formation of Crystals by Voltaic Electricity—Photo-galvanic Engraving—Conduction—Heat of Voltaic Electricity—Electric Fish.
Voltaic or Dynamic electricity is elicited by the force of chemical action. It is connected with some of the most brilliant periods of British science, from the splendid discoveries to which it led Sir Humphry Davy and Dr. Faraday.
In 1790, while Galvani, Professor of Anatomy in Bologna, was making experiments on electricity, he was surprised to see convulsive motions in the limbs of a dead frog accidentally lying near the machine during an electrical discharge. Though a similar action had been noticed long before his time, he was so much struck with this singular phenomenon, that he examined all the circumstances carefully, and at length found that convulsions take place when the nerve and muscle of a frog are connected by a metallic conductor. This excited the attention of all Europe; and it was not long before Volta, Professor at Pavia, showed that the mere contact of different bodies is sufficient to disturb electrical equilibrium, and that a current of electricity flows in one direction through a circuit of three conducting substances. From this he was led, by acute reasoning and experiment, to the construction of the Voltaic pile, which, in its early form, consisted of alternate discs of zinc and copper, separated by pieces of wet cloth, the extremities being connected by wires. This simple apparatus, perhaps the most wonderful instrument that has been invented by the ingenuity of man, by divesting electricity of its sudden and uncontrollable violence, and giving in a continued stream a greater quantity at a diminished intensity, has exhibited that force under a new and manageable form, possessing powers the most astonishing and unexpected. The expression current has no relation to a fluid, which is now considered to be as inconsistent with the phenomena of dynamic as with static electricity. 298It was shown by Grotthus that the transmission of Voltaic electricity through liquids consists of a series of chemical affinities acting in definite directions; and Mr. Grove, from an examination of its action on the various kinds of matter, has come to the same conclusion. Indeed it is now the generally received opinion that a current of electricity is merely a continuous transmission of chemical affinity from particle to particle of the substance through which it is passing, and consequently that it is a continuous transmission of force. As the Voltaic battery has become one of the most important engines of physical research, some account of its present condition may not be out of place.
The disturbance of electric equilibrium, and a development of electricity, invariably accompany the chemical action of a fluid on metallic substances, and the electricity is most plentiful when that action occasions oxidation. Metals vary in the quantity of electricity afforded by their combination with oxygen. But the greatest abundance is developed by the oxidation of zinc by weak sulphuric acid. And, in conformity with the law that one kind of electricity cannot be evolved without an equal quantity of the other being brought into activity, it is found that the acid is positively, and the zinc negatively electric. It has not yet been ascertained why equilibrium is not restored by the contact of these two substances, which are both conductors, and in opposite electrical states. However, the electrical and chemical changes are so connected, that, unless equilibrium be restored, the action of the acid will go on languidly, or stop as soon as a certain quantity of electricity is accumulated in it. Equilibrium, nevertheless, will be restored, and the action of the acid will be continuous, if a plate of copper be placed in contact with the zinc, both being immersed in the fluid; for the copper, not being acted upon by the acid, will serve as a conductor to convey the positive electricity from the acid to the zinc, and will at every instant restore the equilibrium, and then the oxidation of the zinc will go on rapidly. Thus three substances are concerned in forming a Voltaic circuit, but it is indispensable that one of them should be a fluid. The electricity so obtained will be very feeble in overcoming resistances offered by imperfect conductors interposed in the circuit, or by very long wires, but it may be augmented by increasing the number of plates. In the common Voltaic battery, the electricity which the fluid has acquired from 299the first plate of zinc exposed to its action is taken up by the copper plate belonging to the second pair, and transferred to the second zinc plate, with which it is connected. The second plate of zinc, possessing equal powers, and acting in conformity with the first, having thus acquired a larger portion of electricity than its natural share, communicates a larger quantity to the fluid in the second cell. This increased quantity is again transferred to the next pair of plates; and thus every succeeding alternation is productive of a further increase in the quantity of the electricity developed. This action, however, would stop unless a vent were given to the accumulated electricity, by establishing a communication between the positive and negative poles of the battery by means of wires attached to the extreme plate at each end. When the wires are brought into contact, the Voltaic circuit is completed, the electricities meet and neutralize each other, producing the shock and other electrical phenomena; and then the electric current continues to flow uninterruptedly in the circuit, as long as the chemical action lasts. The stream of positive electricity flows from the zinc to the copper. The construction and power of the Voltaic battery have been much improved of late years, but the most valuable improvement is the constant battery of Professor Daniell. In all batteries of the ordinary construction, the power, however energetic at first, rapidly diminishes, and ultimately becomes very feeble. Professor Daniell found that this diminution of power is occasioned by the adhesion of the evolved hydrogen to the surface of the copper, and by the precipitation of the sulphate formed by the action of the acid on the zinc. He prevents the latter by interposing between the copper and the zinc, in the cell containing the liquid, a membrane which, without impeding the electric current, prevents the transfer of the salt; and the former, by placing between the copper and the membrane solution of sulphate of copper, which being reduced by the hydrogen prevents the adhesion of this gas to the metallic surface. Each element of the battery consists of a hollow cylinder of copper, in the axis of which is placed a cylindrical rod of zinc; between the zinc and the copper a membranous bag is placed, which divides the cell into two portions, the inner of which is filled with dilute acid, and the one nearer the copper is supplied with crystals of the sulphate of that metal. The battery consists of several of these elementary cells connected together by metallic wires, the zinc rod of one with the copper cylinder of that 300next to it. The zinc rods are amalgamated, so that local action, which, in ordinary cases, is so destructive of the zinc, does not take place, and no chemical action is manifested unless the circuit be completed. The rods are easily detached, and others substituted for them when worn out. This battery, which possesses considerable power, and is constant in its effects for a very long time, is greatly superior to all former arrangements, either as an instrument of research, or for exhibiting the ordinary phenomena of Voltaic electricity.
A battery charged with water alone, instead of acid, is constant in its action, but the quantity of electricity it develops is comparatively very small. Mr. Cross, of Broomfield in Somersetshire, kept a battery of this kind in full force during twelve months. M. Becquerel had invented an instrument for comparing the intensities of the different kinds of electricity by means of weights; but, as it is impossible to make the comparison with Voltaic electricity produced by the ordinary batteries, on account of the perpetual variation to which the intensity of the current is liable, he has constructed a battery which affords a continued stream of electricity of uniform power, but it is also of very feeble force. The current is produced by the chemical combination of an acid with an alkali.
Metallic contact is not necessary for the production of Voltaic electricity, which is entirely due to chemical action. The intensity of the Voltaic electricity is in proportion to the intensity of the affinities concerned in its production, and the quantity produced is in proportion to the quantity of matter which has been chemically active during its evolution. Dr. Faraday considers this definite production to be one of the strongest proofs that electricity is of chemical origin.
Galvanic or Voltaic electricity is manifested by two continuous forces or currents passing in opposite directions through the circuit: the zinc is the positive end or pole of the battery, and the copper the negative.
Voltaic electricity is distinguished by two marked characters. Its intensity increases with the number of plates, its quantity with the extent of their surfaces. The most intense concentration of force is displayed by a numerous series of large plates: light and heat are copiously evolved, and chemical decomposition is accomplished with extraordinary energy; whereas the electricity from one pair of plates, whatever their size may be, is so feeble 301that it gives no sign either of attraction or repulsion. Common or static electricity is of greater intensity and has a greater power of overcoming resistance than Voltaic electricity, but it acts upon a smaller quantity of matter. However, by diminishing the size of the plates, and increasing their number, the intensity of a battery may be increased till it becomes equal to that of the electrical machine.
The action of Voltaic electricity differs in some respects materially from that of the ordinary kind. When a quantity of common electricity is accumulated, the restoration of equilibrium is attended by an instantaneous violent explosion, accompanied by the development of light, heat, and sound. The concentrated power of the electricity forces its way through every obstacle, disrupting and destroying the cohesion of the particles of the bodies through which it passes, and occasionally increasing its destructive effects by the conversion of fluids into steam from the intensity of the momentary heat, as when trees are torn to pieces by a stroke of lightning. Even the vivid light which marks the path of the electricity is probably owing in part to the sudden compression of the air and the rapidity of its passage. But the instant equilibrium is restored by this energetic action the whole is at an end. On the contrary, when an accumulation takes place in a Voltaic battery, equilibrium is restored the moment the circuit is completed. But so far is the electric stream from being exhausted, that it continues to flow silently and invisibly in an uninterrupted current supplied by a perpetual reproduction. And, although its action on bodies is neither so sudden nor so intense as that of common electricity, yet it acquires such power from constant accumulation and continued action, that it ultimately surpasses the energy of the other. The two kinds of electricity differ in no circumstance more than in the development of heat. Instead of a momentary evolution, the circulation of the Voltaic electricity is accompanied by a continued development of heat, lasting as long as the circuit is complete, without producing either light or sound. Its intensity from a very powerful battery is greater than that of any heat that can be obtained by artificial means, so that it fuses substances which resist the action of the most powerful furnaces. The temperature of every part of a Voltaic battery itself is raised during its activity. With the greater number of metals Mr. Grove 302found that the positive terminal or pole is hotter than the negative.
According to Mr. Joule, the quantity of heat generated in a unit of time is proportional to the strength of the current, and when a galvanic current is employed in chemical analysis, the heat in the entire circuit generated in a unit of time is equal to the work expended in producing it, minus that employed in the analysis. In fact, a current of electricity cannot pass through a homogeneous conductor without generating heat in overcoming resistance, an effect proved by Mr. Joule to be proportional to the square of the force of the current, and the same in whatever direction the current may be flowing. Any other thermal action that can take place must depend upon the heterogeneousness of the circuit, and must be reversible with the current. For example, if a semicircle of bismuth be joined to a semicircle of antimony, an electric current in passing through it produces cold where it passes from the bismuth to the antimony by absorption, and heat where it passes from the antimony to the bismuth.
The transit of the electricity from pole to pole is accompanied by light, and in consequence of the continuous current sparks occur every time the contact of the wires is either broken or renewed; but considerable intensity is requisite to enable the electricity to force its way through atmospheric air or gas. Both its length and colour are affected by the density of the medium through which it passes. If the medium be gradually rarefied the discharge increases from a spark to a luminous glow, differing in colour in different gases, but white in air. When very much attenuated a discharge may be made to pass across 6 or 7 feet of space, while in air of the ordinary density it will not pass through an inch. In rarefied gas it resembles the Aurora by its continuous flashes. When the battery is powerful the luminous effects are very brilliant.
The most splendid artificial light known is produced by fixing pencils of charcoal at the extremities of the wires, and bringing them into contact. This light is the more remarkable as it is independent of combustion, since the charcoal suffers no apparent change, and, likewise, because it is equally vivid in such gases as do not contain oxygen. It depends upon the molecular arrangement of the charcoal; for Mr. Grove observes that “carbon in a transparent crystalline 303state, as diamond, is as perfect a non-conductor as we know, while in an opaque amorphous state, as graphite or charcoal, it is one of the best conductors: thus in one state it transmits light and stops electricity, in the other it transmits electricity and stops light. It is a circumstance worthy of remark, that the arrangement of molecules which renders a solid body capable of transmitting light is most unfavourable to the transmission of electricity, transparent solids being very imperfect conductors of electricity; so all gases readily transmit light, but are amongst the worst conductors of electricity, if indeed they can be said to conduct it at all. The fact that the molecular structure or arrangement of a body influences, indeed I may say determines, its conducting power, is by no means explained by the theory of a fluid; but if electricity be only a transmission of force or motion, the influence of the molecular state is just what would be expected.”
Professor Wheatstone, by fixing metallic points at the extremities of the wires or poles, has found that the appearance of the spectrum of the voltaic arc or vivid flame that is seen between the terminals of a battery, depends, as in static electricity, upon the metal from whence it is taken. The spectrum of that from mercury consists of seven definite rays, separated from each other by dark intervals; these visible rays are two orange lines close together, a bright green line, two blueish-green lines near each other, a very bright purple line, and, lastly, a blue line. It is the same when it passes through carbonic acid gas, oxygen gas, air, or vacuum. The light from zinc, cadmium, tin, bismuth, and lead, in a melted state, gives similar results; but the number, position, and colour of the lines vary so much in each case, and the appearances are so different, that the metals may easily be distinguished from one another by this mode of investigation. The electric spark is considered by M. Angström to be the overlapping of two spectra, one of which belongs to the metal, and the other to the gas through which the spark passes, and that the bright lines vary with the gas as well as with the metal. In an oxygen spectrum the greatest number of bright lines occur in the blue and violet, in nitrogen in the green and yellow, and in hydrogen in the red. These effects must necessarily be connected with the chemical and thermal properties of the gases.
Mr. Grove considers that the colour of the voltaic arc, or flame, 304which appears between the poles of a very powerful battery, depends upon the substance of the metal from whence it proceeds and on the medium through which it passes. The spark from zinc is blue, from silver it is green, from iron it is red and scintillating—precisely the colours afforded by these metals in their ordinary combustion. But the colour varies also with the medium through which the light passes, for when the medium is changed a change takes place in the colour, showing an affection of the intervening matter. A portion of the metal terminals or poles is actually transmitted with every electrical or Voltaic discharge, whence Mr. Grove concludes that the electrical discharge arises, at least in part, from an actual repulsion and severance of the electrified matter itself, which flies off at the points of least resistance. He observes that “the phenomena attending the electric spark or Voltaic arc tends to modify considerably our previous idea of the nature of the electric force as a producer of ignition and combustion. The Voltaic arc is perhaps, strictly speaking, neither ignition nor combustion. It is not simply ignition; because the matter of the terminals is not merely brought to a state of incandescence, but is physically separated, and partially transferred from one terminal to another, much of it being dissipated in a vaporous state. It is not combustion; for the phenomena will take place independently of atmospheric air, oxygen gas, or any of the bodies usually called supporters of combustion; combustion being in fact chemical union attended with heat and light. In the Voltaic arc we may have no chemical union, for if the experiment be performed in an exhausted receiver, or in nitrogen, the substance forming the terminals is condensed and precipitated upon the interior of the vessel, in, chemically speaking, an unaltered state. Thus, to take a very striking example, if the Voltaic discharge be taken between zinc terminals in an exhausted receiver, a fine black powder of zinc is deposited on the sides of the receiver; this can be collected, and takes fire readily in air by being touched with a match, or ignited wire, instantly burning into white oxide of zinc. To an ordinary observer the zinc would appear to be burned twice—first in the receiver, where the phenomenon presents all the appearance of combustion, and, secondly, in the real combustion in air. With iron the experiment is equally instructive. Iron is volatilized by the Voltaic arc in nitrogen, or in an exhausted 305receiver; and when a scarcely perceptible film has lined the receiver, if it be washed with an acid, it then gives, with ferrocyanide of potassium, the Prussian-blue precipitate. In this case we readily distil iron, a metal by ordinary means fusible only at a very high temperature.”
Another strong evidence that the Voltaic discharge consists of the material itself of which the terminals are composed, is the peculiar rotation which is observed in the light when iron is employed, the magnetic character of this metal causing its particles to rotate by the influence of the Voltaic current. In short, Mr. Grove concludes that, although it would be hasty to assert that the electrical disruptive discharge can in no case take place without the terminals being affected, yet he had met with no instance of such a result, provided the discharge had been sufficiently prolonged, and the terminals in such a state as could be expected to render manifest slight changes![15]
Some years ago Mr. Grove discovered that the electrical discharge possesses certain phases or fits of an alternate character, forming rings of alternate oxidation and deoxidation on metallic surfaces. A highly polished silver plate in an air-pump was connected with the pole of a powerful inductive battery, while a fine metallic wire, or even a common sewing needle, was fixed at the other pole, and so arranged as to be perpendicular to the silver plate, and very near, but not touching it. By means of this apparatus the electrical discharge could be sent through any kind of rarefied media. In some of the experiments a series of concentric coloured rings of oxide alternating with rings of polished or unoxidated silver were formed on the plate under the point of the needle or wire. When the plate was previously coated with a film of oxide, the oxide was removed in concentric spaces by the discharge, and increased on the alternate ones, showing an alternate positive and negative electricity, or electricity of an opposite character in the same discharge.
When the silver plate was polished the centre of the rings formed on it was yellow-green surrounded by blue-green; then a ring of polished silver, followed by a crimson ring with a slight orange tint on the inner side and deep purple on the outer; 306lastly the indication of a polished one. When the air-pump was filled with attenuated olefiant gas the rings were precisely the same with those seen in thin plates; hence the effect is the same as that produced by the interference of light. In these experiments the luminous appearance extended from three quarters of an inch to an inch round the point of the needle or wire.
When the silver plate was connected with the negative pole of the battery a polished point appeared upon it opposite the needle, surrounded by a dusky ill-defined areola of a brown colour tinged with purple when viewed in one direction, and greenish-white when seen in another.
In the present year Mr. Gassiot, Vice-President of the Royal Society, has shown that the stratified character of the electric discharge is remarkably developed in the Torricellian vacuum. Among the various experiments made by that gentleman two may be selected as strongly illustrative of this new and singular property of electrical light.
In a closed glass tube about an inch internal diameter and 38 inches long, in which a vacuum had been made, two platinum wires were hermetically sealed, 32 inches apart, and connected with the poles of an inductive battery. The luminous appearance at the two poles was very different when electricity passed through the wires. A glow surrounded the negative pole, and in close approximation to the glow a well-defined dark space appeared, while from the positive pole or wire the light proceeded in a stream; but unless the charge be great or the tube short, the stream will not extend to the black band, which is totally different from the intervening space. When discharges of electricity were sent through this vacuum tube a series of bands or stratifications were formed which were concave towards the positive pole; and as in the changes in making and breaking the circuit the electricity emanates from the different terminals or wires, their concavities were in opposite directions.
When instead of platinum wires narrow tinfoil coatings were placed round the exterior of the glass tube and connected with the wires of the battery, brilliant stratifications filled the interior of the tube between the foil coatings, but no dark band appeared. At present Mr. Gassiot is inclined to believe that the dark band is due to interference; but that the stratifications arise from pulsations or impulses of a force acting in a highly attenuated but 307resisting medium, for even with the best air-pumps it is impossible to make a perfect void; he is still occupied with experiments on this new subject, and no doubt will obtain very remarkable results, of which none can be more extraordinary than his discovery of the powerful influence of the magnet on this electric light. The stratifications are formed in rapid succession in the tube with platinum wires and are turned different ways, but they can be separated at any part of the tube by the pole of a magnet round which the whole stratifications have a tendency to revolve. In the second experiment, where the tinfoil was used, the discharge was divided in two by the pole of a magnet, and the two parts had a tendency to rotate round the magnet in opposite directions.
Voltaic electricity is a powerful agent in chemical analysis. When transmitted through conducting fluids, it separates them into their constituent parts, which it conveys in an invisible state through a considerable space or quantity of liquid to the poles, where they come into evidence. Numerous instances might be given, but the decomposition of water is perhaps the most simple and elegant. Suppose a glass tube filled with water, and corked at both ends; if one of the wires of an active Voltaic battery be made to pass through one cork, and the other through the other cork, into the water, so that the extremities of the two wires shall be opposite and about a quarter of an inch asunder, chemical action will immediately take place, and gas will continue to rise from the extremities of both wires till the water has vanished. If an electric spark be then sent through the tube, the water will reappear. By arranging the experiment so as to have the gas given out by each wire separately, it is found that water consists of two volumes of hydrogen and one of oxygen. The hydrogen is given out at the positive wire of the battery, and the oxygen at the negative. The oxides are also decomposed; the oxygen appears at the positive pole, and the metal at the negative. The decomposition of the alkalies and earths by Sir Humphry Davy formed a remarkable era in the history of science. Soda, potash, lime, magnesia, and other substances heretofore considered to be simple bodies incapable of decomposition, were resolved by electric agency into their constituent parts, and proved to be metallic oxides, by that illustrious philosopher. All chemical changes produced by electricity are accomplished on the same principle; and it appears that, in general, combustible 308substances, metals, and alkalies go to the negative wire, while acids and oxygen are evolved at the positive. The transfer of these substances to the poles is not the least wonderful effect of the Voltaic battery. Though the poles be at a considerable distance from one another, nay, even in separate vessels, if a communication be only established by a quantity of wet thread, as the decomposition proceeds the component parts pass through the thread in an invisible state, and arrange themselves at their respective poles. According to Dr. Faraday, electro-chemical decomposition is simply a case of the preponderance of one set of chemical affinities more powerful in their nature over another set which are less powerful. And in electro-chemical action of any kind produced by a continuous current, the amount of action in a given time is nearly, if not rigorously, proportional to the strength of the current. The great efficacy of Voltaic electricity in chemical decomposition arises not from its tension, but from the quantity set in motion and the continuance of its action. Its agency appears to be most exerted on fluids and substances which by conveying the electricity partially and imperfectly impede its progress. But it is now proved to be as efficacious in the composition as in the decomposition or analysis of bodies.
It had been observed that, when metallic solutions are subjected to galvanic action, a deposition of metal, sometimes in the form of minute crystals, takes place on the negative wire. By extending this principle, and employing a very feeble Voltaic action, M. Becquerel has succeeded in forming crystals of a great proportion of the mineral substances, precisely similar to those produced by nature. The electric state of metallic veins makes it possible that many natural crystals may have taken their form from the action of electricity bringing their ultimate particles, when in solution, within the narrow sphere of molecular attraction. Both light and motion favour crystallization. Crystals which form in different liquids are generally more abundant on the side of the jar exposed to the light; and it is well known that still water, cooled below 32°, starts into crystals of ice the instant it is agitated. A feeble action is alone necessary, provided it be continued for a sufficient time. Crystals formed rapidly are generally imperfect and soft, and M. Becquerel found that even years of constant Voltaic action were necessary for the 309crystallization of some of the hard substances. If this law be general, how many ages may be required for the formation of a diamond!
The deposition of metal from a metallic solution by galvanic electricity has been most successfully applied to the arts of plating and gilding, as well as to the more delicate process of copying medals and copper plates. Indeed, not medals only, but any object of art or nature, may be coated with precipitated metal, provided it be first covered with the thinnest film of plumbago, which renders a non-conductor sufficiently conducting to receive the metal. Photo-galvanic engraving depends upon this. Gelatine mixed with bichromate of potash, nitrate of silver, and iodide of potassium, is spread over a plate of glass, and when dry a positive print is laid upon it with its face downwards, which, when exposed to the sun, leaves its impression. When soaked in water the gelatine swells around all those parts where the light had fallen, thus forming an intaglio, a cast of which is taken in gutta-percha, which is then coated with copper by the electro process, whence a copper plate in relief is obtained.
Static electricity, on account of its high tension, passes through water and other liquids as soon as it is formed, whatever the length of its course may be. Voltaic electricity, on the contrary, is weakened by the distance it has to traverse. Pure water is a very bad conductor; but ice absolutely stops a current of Voltaic electricity altogether, whatever be the power of the battery, although static or common electricity has sufficient power to overcome its resistance. Dr. Faraday has discovered that this property is not peculiar to ice; that, with a few exceptions, bodies which do not conduct electricity when solid acquire that property, and are immediately decomposed, when they become fluid, and, in general, that decomposition takes place as soon as the solution acquires the capacity of conduction, which has led him to suspect that the power of conduction may be only a consequence of decomposition.
Heat increases the conducting power of some substances for Voltaic electricity, and of the gases for both kinds. Dr. Faraday has given a new proof of the connexion between heat and electricity, by showing that, in general, when a solid, which is not a metal, becomes fluid, it almost entirely loses its power of conducting 310heat, while it acquires a capacity for conducting electricity in a high degree. M. Becquerel regards the production of heat and that of electricity to be concomitant; their dependence being such, that when one is increased the other diminishes, and vice versâ, so that one may altogether disappear with the increase of the other. For instance, when electricity circulates in a metallic wire, the greater the heat produced, the less the quantity of electricity which passes, and the contrary, so that the affair proceeds as if electricity were converted into heat, and heat into electricity. Again, in a closed galvanic circuit the sum of the heat produced in the chemical action of the acidulated water upon the zinc and in the conducting wire is constant, so that the quantity of heat disengaged in the reaction is greater in proportion as less electricity passes through the wire. These, and other circumstances, prove such an intimate connexion between the production of heat and electricity, that in the change of condition of substances the electrical effects might disappear or be annulled by the calorific effects.
The galvanic current affects all the senses: nothing can be more disagreeable than the shock, which may even be fatal if the battery be very powerful. A bright flash of light is perceived with the eyes shut, when one of the wires touches the face, and the other the hand. By touching the ear with one wire, and holding the other, strange noises are heard; and an acid taste is perceived when the positive wire is applied to the tip of the tongue, and the negative wire touches some other part of it. By reversing the poles the taste becomes alkaline. It renders the pale light of the glow-worm more intense. Dead animals are roused by it, as if they started again into life, and it may ultimately prove to be the cause of muscular action in the living.
Several fish possess the faculty of producing electrical effects. The most remarkable are the gymnotus electricus, found in South America; and the torpedo, a genus of ray, frequent in the Mediterranean. The electrical action of the torpedo depends upon an apparatus apparently analogous to the Voltaic pile, which the animal has the power of charging at will, consisting of membranous columns filled throughout with laminæ, separated from one another by a fluid. The absolute quantity of electricity brought into circulation by the torpedo is so great, that it effects 311the decomposition of water, has power sufficient to make magnets, gives very severe shocks and the electric spark. It is identical in kind with that of the galvanic battery, the electricity of the under surface of the fish being the same with the negative pole, and that in the upper surface the same with the positive pole. Its manner of action is, however, somewhat different; for, although the evolution of the electricity is continued for a sensible time, it is interrupted, being communicated by a succession of discharges.
Discovery of Electro-magnetism—Deflection of the Magnetic Needle by a Current of Electricity—Direction of the Force—Rotatory Motion by Electricity—Rotation of a Wire and a Magnet—Rotation of a Magnet about its Axis—Of Mercury and Water—Electro-Magnetic Cylinder or Helix—Suspension of a Needle in a Helix—Electro-Magnetic Induction—Temporary Magnets—The Galvanometer.
The disturbing effects of the aurora and lightning on the mariner’s compass had been long known. In the year 1819 M. Oersted, Professor of Natural Philosophy at Copenhagen, discovered that a current of Voltaic electricity exerts a powerful influence on a magnetized needle. This observation has given rise to the theory of electro-magnetism—one of the most interesting sciences of modern times, whether it be considered as leading us a step farther in generalization, by identifying two agencies hitherto referred to different causes, or as developing a new force, unparalleled in the system of the world, which, overcoming the retardation from friction, and the obstacle of a resisting medium, maintains a perpetual motion as long as the action of a Voltaic battery is continued.
When the two poles of a Voltaic battery are connected by a metallic wire, so as to complete a circuit, the electricity flows without ceasing. If a straight portion of that wire be placed parallel to, and horizontally above, a magnetized needle at rest in the magnetic meridian, but freely poised like the mariner’s compass, the action of the electric current flowing through the wire will instantly cause the needle to change its position. Its extremity will deviate from the north towards the east or west, according to the direction in which the current is flowing; and, on reversing the direction of the current, the motion of the needle will be reversed also. The numerous experiments that have been made on magnetism and electricity, as well as those on the various relative motions of a magnetic needle under the influence of galvanic electricity, arising from all possible positions of the conducting wire, and every direction of the Voltaic current, together with all the other phenomena of electro-magnetism, are 313explained by Dr. Roget in some excellent articles on these subjects in the Library of Useful Knowledge.
All experiments tend to prove that the force emanating from the electric current, which produces such effects on the magnetic needle, acts at right angles to the current. The action of an electrical current upon either pole of a magnet has no tendency to cause the pole to approach or recede, but to rotate about it. If the stream of electricity be supposed to pass through the centre of a circle whose plane is perpendicular to the current, the direction of the force exerted by the electricity will always be in the tangent to the circle, or at right angles to its radius (N. 223). Consequently, the tangential force of the electricity has a tendency to make the pole of a magnet move in a circle round the wire of the battery.
Rotatory motion was suggested by Dr. Wollaston. Dr. Faraday was the first who actually succeeded in making the pole of a magnet rotate about a vertical conducting wire. In order to limit the action of the electricity to one pole, about two-thirds of a small magnet were immersed in mercury, the lower end being fastened by a thread to the bottom of the vessel containing the mercury. When the magnet was thus floating almost vertically with its north pole above the surface, a current of positive electricity was made to descend perpendicularly through a wire touching the mercury, and immediately the magnet began to rotate from left to right about the wire. The force being uniform, the rotation was accelerated till the tangential force was balanced by the resistance of the mercury, when it became constant. Under the same circumstances the south pole of the magnet rotates from right to left. It is evident, from this experiment, that the wire may also be made to perform a rotation round the magnet, since the action of the current of electricity on the pole of the magnet must necessarily be accompanied by a corresponding reaction of the pole of the magnet on the electricity in the wire. This experiment has been accomplished by a vast number of contrivances, and even a small battery, consisting of two plates, has performed the rotation. Dr. Faraday produced both motions at the same time in a vessel containing mercury; the wire and the magnet revolved in one direction about a common centre of motion, each following the other.
The next step was to make a magnet, and also a cylinder, revolve about their own axes, which they do with great rapidity. 314Mercury has been made to rotate by means of Voltaic electricity, and Professor Ritchie exhibited in the Royal Institution the singular spectacle of the rotation of water by the same means, while the vessel containing it remained stationary. The water was in a hollow double cylinder of glass, and, on being made the conductor of electricity, was observed to revolve in a regular vortex, changing its direction as the poles of the battery were alternately reversed. Professor Ritchie found that all the different conductors hitherto tried by him, such as water, charcoal, &c., give the same electro-magnetic results when transmitting the same quantity of electricity, and that they deflect the magnetic needle in an equal degree when their respective axes of conduction are at the same distance from it. But one of the most extraordinary effects of this force is exhibited by coiling a copper wire, so as to form a helix or corkscrew, and connecting the extremities of the wire with the poles of a galvanic battery. If a magnetized steel bar or needle be placed within the screw, so as to rest upon the lower part, the instant a current of electricity is sent through the wire of the helix, the steel bar starts up by the influence of this invisible power, and remains suspended in the air in opposition to the force of gravitation (N. 224). The effect of the electro-magnetic power exerted by each turn of the wire is to urge the north pole of the magnet in one direction, and the south pole in the other. The force thus exerted is multiplied in degree and increased in extent by each repetition of the turns of the wire, and in consequence of these opposing forces the bar remains suspended. This helix has all the properties of a magnet while the electrical current is flowing through it, and may be substituted for one in almost every experiment. It acts as if it had a north pole at one extremity and a south pole at the other, and is attracted and repelled by the poles of a magnet exactly as if it were one itself. All these results depend upon the course of the electricity; that is, on the direction of the turns of the screw, according as it is from right to left, or from left to right, being contrary in the two cases.
The action of Voltaic electricity on a magnet is not only precisely the same with the action of two magnets on one another, but its influence in producing temporary magnetism in iron and steel is also the same with magnetic induction. The term induction, when applied to electric currents, expresses the power 315which these currents possess of inducing a particular state upon matter in their immediate neighbourhood, otherwise neutral or indifferent. For example, the connecting wire of a galvanic battery holds iron filings suspended like a magnet as long as the current continues to flow through it: the iron becomes magnetic by the induction of the current. The most powerful temporary magnets are obtained by bending a thick cylinder of soft iron into the form of a horseshoe, and surrounding it with a coil of thick copper wire covered with silk to prevent communication between its coils. When this wire forms part of a galvanic circuit the iron becomes so highly magnetic by the induction of the current flowing through the wire that a temporary magnet of this kind made by Professor Henry of the Albany Academy in the United States sustained a weight of nearly a ton. Another by Mr. Gage has been applied with considerable success as a moving power: its spark is a bright flash, and the snap as loud as a pistol. But the most powerful known is that employed by Mr. Joule in his experiments, which sustains a weight of 2080 lbs. The iron loses its magnetism the instant the electricity ceases to flow, and acquires it again as instantaneously when the circuit is renewed.
The action of an electric current causes a deviation of the compass from the plane of the magnetic meridian. In proportion as the needle recedes from the meridian, the intensity of the force of terrestrial magnetism increases, while at the same time the electro-magnetic force diminishes; the number of degrees at which the needle stops, showing where the equilibrium between these two forces takes place, will indicate the intensity of the galvanic current. The galvanometer, constructed upon this principle, is employed to measure the intensity of galvanic currents collected and conveyed to it by wires. This instrument is rendered much more sensible by neutralizing the effects of the earth’s magnetism on the needle, which is accomplished by placing a second magnetised needle so as to counteract the action of the earth on the first—a precaution requisite in all delicate magnetical experiments.
It has been ascertained by means of this instrument that the action of an electrical current upon a magnet is inversely as the square of the distance, and the energy with which an electro magnet acts is directly as the power of the galvanic battery and the number of coils round the core, and inversely as the resistance of the wire.
Electro-Dynamics—Reciprocal Action of Electric Currents—Identity of Electro-Dynamic Cylinders and Magnets—Differences between the Action of Voltaic Electricity and Electricity of Tension—Effects of a Voltaic Current—Ampère’s Theory—Dr. Faraday’s Experiment of Electrifying and Magnetising a Ray of Light.
The science of electro-magnetism, which must render the name of M. Oersted ever memorable, relates to the reciprocal action of electrical and magnetic currents: M. Ampère, by discovering the mutual action of electrical currents on one another, has added a new branch to the subject, to which he has given the name of electro-dynamics.
When electric currents are passing through two conducting wires, so suspended or supported as to be capable of moving both towards and from one another, they show mutual attraction or repulsion, according as the currents are flowing in the same or in contrary directions; the phenomena varying with the relative inclinations and positions of the streams of electricity. The mutual action of such currents, whether they flow in the same or in contrary directions, whether they be parallel, perpendicular, diverging, converging, circular, or heliacal, all produce different kinds of motion in a conducting wire, both rectilineal and circular, and also the rotation of a wire helix, such as that described, now called an electro-dynamic cylinder on account of some improvements in its construction (N. 225). And, as the hypothesis of a force varying inversely as the square of the distance accords perfectly with all the observed phenomena, these motions come under the same laws of dynamics and analysis as any other branch of physics.
Electro-dynamic cylinders act on each other precisely as if they were magnets during the time the electricity is flowing through them. All the experiments that can be performed with the cylinder might be accomplished with a magnet. That end of the cylinder in which the current of positive electricity is moving in a direction similar to the motion of the hands of a watch, acts 317as the south pole of a magnet, and the other end, in which the current is flowing in a contrary direction, exhibits northern polarity.
The phenomena mark a very decided difference between the action of electricity in motion or at rest, that is, between Voltaic and static electricity; the laws they follow are in many respects of an entirely different nature, though the electricities themselves are identical. Since Voltaic electricity flows perpetually, it cannot be accumulated, and consequently has no tension, or tendency to escape from the wires which conduct it. Nor do these wires either attract or repel light bodies in their vicinity, whereas static or ordinary electricity can be accumulated in insulated bodies to a great degree, and in that state of rest the tendency to escape is proportional to the quantity accumulated and the resistance it meets with. In ordinary electricity, the law of action is, that dissimilar electricities attract and similar electricities repel one another. In Voltaic electricity, on the contrary, similar currents, or such as are moving in the same direction, attract one another, while a mutual repulsion is exerted between dissimilar currents, or such as flow in opposite directions. Common electricity escapes when the pressure of the atmosphere is removed, but the electro-dynamical effects are the same whether the conductors be in air or in vacuo.
The effects produced by a current of electricity depend upon the celerity of its motion through a conducting wire. Yet we are ignorant whether the motion be uniform or varied, but the method of transmission has a marked influence on the results; for, when it flows without intermission, it occasions a deviation in the magnetic needle, but it has no effect whatever when its motion is discontinuous or interrupted, like the current produced by the common electrical machine when a communication is made between the positive and negative conductors.
M. Ampère has established a theory of electro-magnetism suggested by the analogy between electro-dynamic cylinders and magnets, founded upon the reciprocal attraction of electro-currents, to which he reduces all the phenomena of magnetism and electro-magnetism, by assuming that the magnetic properties which bodies possess derive these properties from currents of electricity, circulating about every part in one uniform direction. Although every particle of a magnet possesses like properties 318with the whole, yet the general effect is the same as if the magnetic properties were confined to the surface. Consequently, Ampère concludes that the internal electro-currents must compensate one another, and that the magnetism of a body must therefore arise from a superficial current of electricity constantly circulating in a direction perpendicular to the axis of the magnet; so that the reciprocal action of magnets and all the phenomena of electro-magnetism are reduced to the action and reaction of superficial currents of electricity, acting at right angles to their direction.
Notwithstanding the experiments made by Ampère to elucidate the subject, there is still an uncertainty in the theory of the induction of magnetism by an electric current in a body near it. It does not appear whether electric currents which did not previously exist are actually produced by induction, or if its effect be only to give one uniform direction to the infinite number of electric currents previously existing in the particles of the body, and thus rendering them capable of exhibiting magnetic phenomena, in the same manner as polarization reduces the undulations of light to one plane, which had previously been performed in every plane. Possibly both may be combined in producing the effect; for the action of the electric current may not only give a common direction to those already existing, but may also increase their intensity. However that may be, by assuming that the attractions and repulsions of the elementary portions of electric currents vary inversely as the square of the distance, the actions being at right angles to the direction of the current, it is found that the attraction and repulsion of a current of indefinite length on the elementary portion of a parallel current at any distance from it are in the simple ratio of the shortest distance between them: consequently, the reciprocal action of electric currents is reduced to the composition and resolution of forces, so that the phenomena of electro-magnetism are brought under the laws of mechanics by the theory of Ampère. It appears that Dr. Faraday’s very remarkable experiment of electrifying and magnetising a ray of polarized light may possibly afford a demonstration of the reality of Ampère’s explanation of the ultimate nature of magnetism.
In this experiment a copper wire 501 feet long was arranged in four concentric spirals, the extremities of which were connected 319with the poles of a powerful galvanic battery, and a polished prism of heavy glass, or silicated borate of lead, was placed in the axis of the spiral as a core, through the length or axis of which a ray of polarized light was sent. This ray, viewed through a piece of tourmaline or a Nichol’s eye-piece, vanished and reappeared as usual at each quarter revolution of the eye-piece; but when a current of electricity was sent through the spiral at the time the ray had vanished, it instantly reappeared, and remained as long as the electric current continued to flow; but the instant the electricity ceased the light vanished, and as often as the electric current flowed through the spiral, or was interrupted, so often did the polarized ray appear and vanish.
The character of the force thus impressed on the heavy glass is that of rotation, for the stopping and renewing of the electric current had the same effect as the revolving motion of the eye-piece in making the light alternately appear and vanish. Accordingly, Dr. Faraday found that, when the electricity flowed through the spiral in one direction, the rotation of the plane of polarization was right-handed; and when it flowed in the other direction, the rotation of the plane of polarization was left-handed, the rotation increasing with the length of the prism and the intensity of the electricity. The same phenomena were produced by a very powerful magnet when a ray of polarized light was sent through the heavy glass parallel to the line of magnetic force.
Heavy glass or silico-borate of lead has the property more than any other substance of making light rotate under electric and magnetic influence; but many substances have the property more or less, as flint and crown glass, rock salt, all the fixed and essential oils, water, and many other liquids, but none of the gases possess it. In those substances that have the power of circular polarization naturally, the magnetic and electric influences increase or diminish the rotation according to its direction.
Polarized heat is made to revolve in the same manner, when the medium through which it passes is subject to magnetic influence.
Mr. Grove observes that if light and heat be merely modes of force, which there is every reason to believe that they are, it may be fairly stated that in these experiments magnetism affects these forces directly; for light and heat being, in that view, 320motions of ordinary matter, magnetism in affecting these movements affects the forces which occasion them. If, however, this effect of magnetism be a molecular change of the matter transmitting the light and heat, then it follows that the light and heat are indirectly affected by the electricity or magnetism. Dr. Faraday says that the magnetic forces do not act on the ray of light directly, without the intervention of matter, but through the mediation of the substance in which they and the ray have a simultaneous existence; the substances and the forces giving to and receiving from each other the power of acting on the light. Dr. Thomson has shown, by a mathematical investigation of the subject, that Dr. Faraday’s discovery seems to prove the truth of Ampère’s explanation of the ultimate nature of magnetism. However, in Ampère’s theory, the current of electricity flowing round the iron makes it a permanent magnet, but it does not make the heavy glass or the other bodies, which have the same property, either temporary magnets when the light is rotating within them, or permanent magnets when the inductive action of the current of electricity ceases. Hence the molecular condition of the substances, when the light is rotating in them, must be specifically distinct from that of magnetised iron: it must therefore be a new magnetic condition, and the force which the matter in this state possesses must be a new magnetic force.
After describing his admirable experiment, Dr. Faraday observes that “it has established for the first time a true, direct relation and dependence between light and the magnetic and electric forces; and thus a great addition is made to the facts and considerations which tend to prove that all natural forces are tied together, and have one common origin. It is no doubt difficult, in the present state of our knowledge, to express our expectations in exact terms; and though I have said that another of the powers of nature is in these experiments directly related to the rest, I ought perhaps rather to say that another form of the great power is distinctly and directly related to the other forms; or that the great power manifested by particular phenomena in particular forms is here further identified and recognised by the direct relation of its form of light to its forms of electricity and magnetism. The relation existing between polarized light and magnetism and electricity is even more interesting than if it had been shown to exist with common light only. It cannot but 321extend to common light; and, as it belongs to light made in a certain respect more precise in its character and properties by polarization, it collates and connects it with these powers in that duality of character which they possess, and yields an opening, which before was wanting to us, for the appliances of these to the investigation of the nature of this and other radiant agencies.” Thus Dr. Faraday’s experiment not only shows the increasing connexion between the sciences, but the tendency of all the forces of nature to merge in one great and universal power.
In the action of a magnet upon the stratifications of an electrical discharge Mr. Gassiot has discovered a new instance of the connexion between magnetism and light.
Magneto-Electricity—Volta-Electric Induction—Magneto-Electric Induction—Identity in the Action of Electricity and Magnetism—Description of a Magneto-Electric Apparatus and its Effects—Identity of Magnetism and Electricity—The Submarine Telegraph.
From the law of action and reaction being equal and contrary, it might be expected that, as electricity powerfully affects magnets, so, conversely, magnetism ought to produce electrical phenomena. By proving this very important fact from the following series of interesting and ingenious experiments, Dr. Faraday has added another branch to the science which he has named magneto-electricity. A great quantity of copper wire was coiled in the form of a helix round one half of a ring of soft iron, and connected with a galvanic battery; while a similar helix connected with a galvanometer was wound round the other half of the ring, but not touching the first helix. As soon as contact was made with the battery, the needle of the galvanometer was deflected. But the action was transitory; for, when the contact was continued, the needle returned to its usual position, and was not affected by the continual flow of the electricity through the wire connected with the battery. As soon, however, as the contact was broken, the needle of the galvanometer was again deflected, but in the contrary direction. Similar effects were produced by an apparatus consisting of two helices of copper wire coiled round a block of wood, instead of iron, from which Dr. Faraday infers that the electric current passing from the battery through one wire induces a similar current through the other wire, but only at the instant of contact, and that a momentary current is induced in a contrary direction when the passage of the electricity is suddenly interrupted. These brief currents or waves of electricity were found to be capable of magnetizing needles, of passing through a small extent of fluid, and, when charcoal points were interposed in the current of the induced helix, a minute spark was perceived as often as the contacts were made or 323broken, but neither chemical action nor any other electric effects were obtained. A deviation of the needle of the galvanometer took place when common magnets were employed instead of the Voltaic current; so that the magnetic and electric forces are identical in their effects in this experiment. Again, when a helix formed of 220 feet of copper wire, into which a cylinder of soft iron was introduced, was placed between the north and south poles of two bar magnets, and connected with the galvanometer by means of wires from each extremity, as often as the magnets were brought into contact with the iron cylinder it became magnetic by induction, and produced a deflection in the needle of the galvanometer. On continuing the contact the needle resumed its natural position, and, when the contact was broken, deflection took place in the opposite direction; when the magnetic contacts were reversed, the deflection was reversed also. With strong magnets, so powerful was the action, that the needle of the galvanometer whirled round several times successively; and similar effects were produced by the mere approximation or removal of the helix to the poles of the magnets. Thus it was proved that magnets produce the very same effects on the galvanometer that electricity does. Though at that time no chemical decomposition was effected by these momentary currents which emanate from the magnets, they agitated the limbs of a frog; and Dr. Faraday justly observes, that “an agent which is conducted along metallic wires in the manner described, which, whilst so passing, possesses the peculiar magnetic actions and force of a current of electricity, which can agitate and convulse the limbs of a frog, and which finally can produce a spark by its discharge through charcoal, can only be electricity.” Soon after he completely established the identity of the two powers by producing the spark, heating metallic wires, and accomplishing chemical decomposition. Hence it appears that electrical currents are evolved by magnets, which produce the same phenomena with the electrical currents from the Voltaic battery: they, however, differ materially in this respect—that time is required for the exercise of the magnetico-electric induction, whereas Volta-electric induction is instantaneous.
Thus the effect of induction or the influence of the spiral wire in increasing the electric and magnetic power is very great indeed, and to that we are indebted for the electric telegraph, for 324Voltaic electricity alone is too feeble to overcome the resistance of a long wire.
Electric currents, whatever their tension may be, produce the phenomena of induction; these again induce other currents in bodies capable of induction, and so on indefinitely; the first and second flow in the same direction, the others alternately opposite and direct. They all give the shock and can decompose water, but with Volta-electric currents the elevation of temperature as well as their physiological and magnetic effects are produced by instantaneous actions, which only depend upon the quantity and tension of the current, and by no means on its duration, for induced currents only exist for a moment when the circuit of the battery is broken. The most energetic physiological effects are produced by a small quantity of electricity moving with great velocity. The apparatus first employed by Dr. Faraday is in effect a battery, where the agent is the magnetic instead of the Voltaic force, or, in other words, electricity, and is thus constructed:—
A very powerful horseshoe magnet, formed of twelve steel plates in close approximation, is placed in a horizontal position. An armature, consisting of a bar of the purest soft iron, has each of its ends bent at right angles, so that the faces of those ends may be brought directly opposite and close to the poles of the magnet when required. Ten copper wires—covered with silk, in order to insulate them—are wound round one half of the bar of soft iron, as a compound helix: ten other wires, also insulated, are wound round the other half of the bar. The extremities of the first set of wires are in metallic connexion with a circular disc, which dips into a cup of mercury, while the ends of the other ten wires in the opposite direction are soldered to a projecting screw-piece, which carries a slip of copper with two opposite points. The steel magnet is stationary; but when the armature, together with its appendages, is made to rotate vertically, the edge of the disc always remains immersed in the mercury, while the points of the copper slip alternately dip in it and rise above it. By the ordinary laws of induction, the armature becomes a temporary magnet while its bent ends are opposite the poles of the steel magnet, and ceases to be magnetic when they are at right angles to them. It imparts its temporary magnetism to the helices which concentrate it; and, while one set 325conveys a current to the disc, the other set conducts the opposite current to the copper slip. As the edge of the revolving disc is always immersed in the mercury, one set of wires is constantly maintained in contact with it, and the circuit is only completed when a point of the copper slip dips in the mercury also; but the circuit is broken the moment that point rises above it. Thus, by the rotation of the armature, the circuit is alternately broken and renewed; and as it is only at these moments that electric action is manifested, a brilliant spark takes place every time the copper point leaves the surface of the mercury. Platinum wire is ignited, shocks smart enough to be disagreeable are given, and water is decomposed with astonishing rapidity, by the same means; which proves, beyond a doubt, the identity of the magnetic and electric agencies, and places Dr. Faraday, whose experiments established the principle, in the first rank of experimental philosophers.
A magneto-electric machine has been recently constructed by Mr. Henley, of enormous power. It consists of two permanent magnets, from which the induction is obtained; each of these is formed of thirty horseshoe steel magnets, two feet and a half long, and from four to five inches broad, and each is surrounded by a coil of wire six miles long, coated with silk to insulate the coils. A shock from these wires would be instantaneous death. This apparatus will ultimately be employed to send a stream of electricity through long submarine and subterraneous wires; but a Volta-electric machine has hitherto been used, in which the electricity is generated by a galvanic battery instead of magnets.
Induction, or the effect of the spiral wires in augmenting the power of Voltaic electricity, is admirably illustrated in the Atlantic telegraph.
Wires that are to convey electricity under ground, or through water, must be defended from injury and insulated to prevent the lateral escape of the electricity. For that purpose the cable that is laid at the bottom of the Atlantic, from near Valentia in Ireland to Trinity Bay in Newfoundland, is formed of seven fine copper wires which convey the electricity, bound together by a coating of gutta percha, over which there are layers of cloth dipped in pitch, and then the whole is covered by steel wires twisted together in strands and twined round in long close spirals, forming a cord or cable not more than an inch and a quarter in 326diameter, and 2100 miles long. The use of the gutta percha is to insulate the wires; the other coatings are merely for protection.
The Voltaic battery which generates the electricity consists of 40 cells, the plates of which are alternately of zinc and platinized silver, each about nine inches square, the exciting fluid being dilute sulphuric acid. Although the force developed by this battery is so great that a piece of iron three inches long and three eighths of an inch in diameter placed in contact with the poles may be consumed in a few minutes, it is absolutely incapable of sending a current of electricity through wires 2500 miles long, on account of their resistance, without the aid of Dr. Faraday’s inductive action. It is only the primary agent for inducing a current of sufficient strength.
To accomplish that, many thousand yards of fine copper wire coated with silk are wound round a hollow soft iron cylinder; the whole is then coated by gutta percha, and the end of the wire is joined to the wires in the cable so as to form a continuous line from Valentia to Newfoundland. A second copper wire, shorter but thicker than the preceding, and also insulated by a coating of silk, is wound round the cylinder above the gutta percha: when the ends of this thick wire are brought into contact with the poles of the battery, currents of electricity flow through it, between pole and pole, and in their passage temporarily convert the hollow iron cylinder into a powerful electro-magnet, which by its reaction induces a current of electricity in the fine wire of sufficient power to cross the Atlantic. The efficiency of the electric telegraph depends upon the power we possess of breaking and renewing the current at pleasure, since by that means distinct and successive signals are made from station to station. In the Atlantic cable positive and negative electricity are transmitted alternately; the electricity is sent to America from alternate poles, and the current returns again through the water, which completes the circuit.
The passage of electricity through a cable or telegraphic wire in air is sensibly instantaneous; that through a cable, whether extended in water or under ground, requires time on account of lateral induction through the gutta percha; for the electricity, in passing through the wires, induces the opposite electricity on the surface of the water or moist earth in contact with the cable, and in that respect it is precisely like a Leyden jar, the gutta 327percha representing the glass. As the power of induction is proportional to the tension of the electricity, and as the tension is continually diminished by the resistance of the wires, the induction is continually diminished and requires a longer time. Electricity took two seconds to pass through a cable 768 miles long, laid under ground from London to Manchester, and back again twice; while in air it was all but instantaneous, because the inductive capacity of air is very much less than that of water or moist earth. In the experiment with the cable under ground it took two-thirds of a second to overcome the resistance of the wires, and then the velocity of the electricity was 1000 miles in a second, and it was the same whatever the intensity of the electricity.
It has already been mentioned that the efficiency of the electric telegraph depends upon the breaking and renewing the current of electricity by means of which a succession of waves of electricity are sent through the conducting wires. Now it has been ascertained that three electric waves may travel simultaneously through the wires of the Atlantic telegraph with sufficient intervals between them to record the indications they are intended to convey; that is, three signals can be intelligibly and practically transmitted in two seconds.
The original design, structure, and difficulty of depositing the cable are only equalled by the talent and perseverance with which it has been done. The 5th of August, 1858, will be memorable for the accomplishment of the boldest enterprise that ever was undertaken by man, and which is only the beginning of a vast submarine communication that will ultimately encircle the globe. It has been granted to British genius thus to annihilate time and space, in order to connect all mankind into one great family for their moral and religious advancement; and, whatever may be the fate of the British Islands in the course of ages, to their energetic race the glory will remain of having been the chief instruments in the hands of Providence for the civilization of the world—a civilization which will extend with the development of their numerous colonies into great independent Christian states, like those of the Union in North America. The thunderbolt snatched from heaven by Franklin now passes through the depths of the Atlantic as a messenger of peace between the kindred nations.[16]
328In telegraphs on land the intensity of the battery or magnets is increased by induction on the same principle. It is by intensity that the electric current is enabled to pass through the wires, and that is augmented by increasing the number of coils round the cylinder: however, it is only advantageous when the distance between the stations is great, for then the resistance in the additional coils bears a small proportion to the resistance offered by very long wires, but a very great proportion to that opposed in very short ones. The nice adjustment for each case has been determined by the experiments of eminent electricians, and all the arrangements have been brought to great perfection in this wonderful triumph of science, which is due to Volta, who called into existence the fiery stream, and to Faraday, who has given it the energy of the lightning.
When the length of the wire in the helices of an electro-magnet is very great, it offers increasing resistance to the passage of the electricity, so that the cessation of magnetism is not instantaneous when the contact with the Voltaic battery is broken. To remedy that defect an instrument has been invented which instantaneously deprives the apparatus of the remaining electricity. A great length of fine wire gives the severest shocks, while a shorter and thicker wire gives the longest sparks and ignites the greatest quantity of platinum wire.
Ruhmkorff’s electro-inductive apparatus has either been improved, or new machines constructed, by Messrs. Grove, Gassiot, and Joule, of intense energy. Indeed, so great is the energy of electro-induction, that hopes were entertained of its superseding steam as a motive power. For the current of electricity from an electro-magnet can be made to flow in opposite directions, so as to produce alternate attractions and repulsions, and consequently a continued motion, which might be applied as a motive force to machinery. However, Mr. Joule has proved that the power developed by one pound of coal in combustion is to that produced by one pound of zinc consumed in Mr. Grove’s powerful electro-magnetic apparatus as nine to one, so that, even if zinc were as cheap as coal, and a Voltaic battery as easily kept in order as an engine-furnace, electricity will not supersede steam as a motive power.
A current of electricity traversing a conductor gives out a quantity of heat determined by fixed laws, the amount of which is invariable as long as the machine to which it is applied remains 329at rest; but the instant the machine is set in motion a reaction takes place in the intensity of the current, causing a diminution in the quantity of heat, because the heat that disappears is converted into the mechanical force exerted by the engine.
Mr. Joule’s experiments prove that, whenever a current of electricity is generated by a magneto-electric machine, the quantity of heat evolved by that current has a constant relation to the power required to work the machine; and on the other hand, whenever an engine is worked by a Voltaic battery, that the power developed is at the expense of the calorific force of the battery for a given consumption of zinc, the mechanical effect produced having a fixed relation to the heat lost in the Voltaic current. The obvious conclusion Mr. Joule draws from these experiments is, that heat and mechanical power are convertible into one another, and it becomes evident, therefore, that heat is either the vis viva or living force of ponderable particles, or a state of attraction and repulsion capable of generating vis viva (N. 222).
Electricity produced by Rotation—Direction of the Currents—Electricity from the Rotation of a Magnet—M. Arago’s Experiment explained—Rotation of a Plate of Iron between the Poles of a Magnet—Relation of Substances to Magnets of three Kinds—Thermo-Electricity.
M. Arago discovered a source of magnetism in rotatory motion. If a circular plate of copper be made to revolve immediately above or below a magnetic needle or magnet, suspended in such a manner that it may rotate in a plane parallel to that of the copper plate, the magnet tends to follow the circumvolution of the plate; or, if the magnet revolves, the plate tends to follow its motion; so powerful is the effect, that magnets and plates of many pounds weight have been carried round. This is quite independent of the motion of the air, since it is the same when a pane of glass is interposed between the magnet and the copper. When the magnet and the plate are at rest, not the smallest effect, attractive, repulsive, or of any kind, can be perceived between them. In describing this phenomenon, M. Arago states that it takes place not only with metals, but with all substances, solids, liquids, and even gases, although the intensity depends upon the kind of substance in motion. Experiments made by Dr. Faraday explain this singular action. He found that, if a piece of metal or a metallic wire forming a circuit of any form be moved from right to left across the lines of force proceeding from the pole of a bar magnet, these lines of force induce a current of electricity flowing in one direction; and when the motion of the metal or wire is reversed, the direction of the current is reversed also: the rotation of the magnet about its axis has no effect on these results, and no current is induced when the metal or wire is at rest. A plate of copper, twelve inches in diameter and one fifth of an inch thick, was placed between the poles of a powerful horseshoe magnet, consequently crossing the magnetic lines of force at right angles, and connected at certain points with a galvanometer by copper wires. When the plate was at rest no effect was produced; but as soon as the plate was 331made to revolve rapidly the galvanometer needle was deflected sometimes as much as 90°, and by a uniform rotation the deflection was constantly maintained at 45°. When the motion of the copper plate was reversed, the needle was deflected in the contrary direction, and thus a permanent current of electricity was evolved by an ordinary magnet. The intensity of the electricity collected by the wires, and conveyed by them to the galvanometer, varied with the position of the plate relatively to the poles of the magnet.
The motion of the electricity in the copper plate may be conceived by considering that, merely by moving a single wire, like the spoke of a wheel, before a magnetic pole, a current of electricity tends to flow through it from one end to the other. Hence, if a wheel be constructed of a great many such spokes, and revolved near the pole of a magnet in the manner of the copper disc, each radius or spoke will tend to have a current produced in it as it passes the pole. Now, as the circular plate is nothing more than an infinite number of radii or spokes in contact, the currents will flow in the direction of the radii if a channel be open for their return; and, in a continuous plate, that channel is afforded by the lateral portions on each side of the particular radius close to the magnetic pole. This hypothesis is confirmed by observation; for the currents of positive electricity set from the centre to the circumference, and the negative from the circumference to the centre, and vice versâ, according to the position of the magnetic poles and the direction of rotation; so that a collecting wire at the centre of the copper plate conveys positive electricity to the galvanometer in one case, and negative in another; that collected by a conducting wire in contact with the circumference of the plate is always the opposite of the electricity conveyed from the centre. It is evident that, when the plate and magnet are both at rest, no effect takes place, since the electric currents which cause the deflection of the galvanometer are only induced by motion across the magnetic lines of force. When the plate is placed edgewise so as to be parallel to these lines of force, no revolution of it with the most powerful magnet produces the slightest signs of a current at the galvanometer. The same phenomena may be produced by electro-magnets. The effects are similar when the magnet rotates and the plate remains at rest. When the magnet revolves uniformly about its own 332axis, electricity of the same kind is collected at its poles, and the opposite electricity at its equator.
The phenomena which take place in M. Arago’s experiments may be explained on this principle. When both the copper plate and the magnet are revolving, the action of the induced electric current tends continually to diminish their relative motion, and to bring the moving bodies into a state of relative rest; so that, if one be made to revolve by an extraneous force, the other will tend to revolve about it in the same direction, and with the same velocity.
When a plate of iron, or of any substance capable of being made either a temporary or permanent magnet, revolves between the poles of a magnet, it is found that dissimilar poles on opposite sides of the plate neutralize each other’s effects, so that no electricity is evolved; while similar poles on each side of the revolving plate increase the quantity of electricity, and a single pole end-on is sufficient. But when copper, and substances not sensible to ordinary magnetic impressions, revolve, similar poles on opposite sides of the plate neutralize each other; dissimilar poles on each side exalt the action; and a single pole at the edge of the revolving plate, or end-on, does nothing. This forms a test for distinguishing the ordinary magnetic force from that produced by rotation. If unlike poles, that is, a north and south pole, produce more effect than one pole, the force will be due to electric currents; if similar poles produce more effect than one, then the power is not electric. These investigations show that there are really very few bodies magnetic in the manner of iron. Dr. Faraday therefore arranges substances in three classes, with regard to their relation to magnets:—those affected by the magnet when at rest, like iron, steel, and nickel, which possess ordinary magnetic properties; those affected when in motion, in which electric currents are evolved by the inductive force of the magnet, such as copper; and, lastly, those which are perfectly indifferent to the magnet, whether at rest or in motion.
It has already been observed that three bodies are requisite to form a galvanic circuit, one of which must be fluid. But, in 1822, Professor Seebeck, of Berlin, discovered that electric currents may be produced by the partial application of heat to a circuit formed of two solid conductors. For example, when a semicircle of bismuth, joined to a semicircle of antimony, so as to form a 333ring, is heated at one of the junctions by a lamp, a current of electricity flows through the circuit from the antimony to the bismuth; and such thermo-electric currents produce all the electro-magnetic effects. A compass needle, placed either within or without the circuit, and at a small distance from it, is deflected from its natural position, in a direction corresponding to the way in which the electricity is flowing. If such a ring be suspended so as to move easily in any direction, it will obey the action of a magnet brought near it, and may even be made to revolve. According to the researches of M. Seebeck, the same substance, unequally heated, exhibits electrical currents; and M. Nobili observed, that in all metals, except zinc, iron, and antimony, the electricity flows from the hot part towards that which is cold. That philosopher attributes terrestrial magnetism to a difference in the action of heat on the various substances of which the crust of the earth is composed; and, in confirmation of his views, he has produced electrical currents by the contact of two pieces of moist clay, of which one was hotter than the other.
M. Becquerel constructed a thermo-electric battery of one kind of metal, by which he has determined the relation between the heat employed and the intensity of the resulting electricity. He found that, in most metals, the intensity of the current increases with the heat to a certain limit, but that this law extends much farther in metals that are difficult to fuse, and which do not rust. The experiments of Professor Cumming show that the mutual action of a magnet and a thermo-electric current is subject to the same laws as those of magnets and galvanic currents; consequently all the phenomena of repulsion, attraction, and rotation may be exhibited by a thermo-electric current. M. Botto, of Turin, has decomposed water and some solutions by thermo-electricity; and the Cav. Antinori of Florence succeeded in obtaining a brilliant spark with the aid of an electro-dynamic coil.
The principle of thermo-electricity has been employed by MM. Nobili and Melloni for measuring extremely minute quantities of heat in their experiments on the instantaneous transmission of radiant heat. The thermo-multiplier, which they constructed for that purpose, consists of a series of alternate bars, or rather fine wires of bismuth and antimony, placed side by side, and the extremities alternately soldered together. When heat is applied 334to one end of this apparatus, the other remaining at its natural temperature, currents of electricity flow through each pair of bars, which are conveyed by wires to a delicate galvanometer, the needle of which points out the intensity of the electricity conveyed, and consequently that of the heat employed. This instrument is so delicate that the comparative warmth of different insects has been ascertained by means of it.
The conservation of force is strictly maintained throughout the whole science and different forms of electricity. In static electricity the positive and negative forces exactly balance one another; they are always simultaneous, and related often by curved lines of force; there is no defect or surplus, and the existence of one kind without the other is utterly impossible—it is absolutely a dual force. The very same may be said of electric currents, whether produced by the Voltaic battery or in any other way—the current in one part of the circuit is absolutely the same in amount and dual character as the other; and in the insulated Voltaic battery, where the sustaining power is internal, not the slightest development of the forces of either of these can occur till the circuit is completed or induction allowed at the extremities; for if when there is no circuit the induction be prevented, not merely no current, but no quantity of electricity at the poles ready to produce a current, can be evolved in the slightest degree.[17]
Magnetism a Dual Power—Antithetic Character of Paramagnetism and Diamagnetism—The Earth Paramagnetic—Properties of Paramagnetic Bodies—Polarity—Induction—Lines of Magnetic Force—Currents of Electricity induced by them—Proved to be Closed Curves—Analogy and Identity of Electricity and Magnetism—Terrestrial Magnetism—Mean Values of the Three Magnetic Elements—Their Variations in Double Progression proved to consist of Two Superposed Variations—Discovery of the Periodicity of the Magnetic Storms—The Decennial Period of the Magnetic Elements the same with that of the Solar Spots—Magnetism of the Atmosphere—Diamagnetism—Action of Electro-Magnetism on Paramagnetic, Diamagnetic Bodies, and on Copper, very different—Proof of Diamagnetic Polarity and Induction—Magnecrystallic Action—Effects of Compression, Heat, and Cleavage on Magnetic Bodies—Mutual Dependence of Light, Heat, Electricity, &c. &c.—The Conservation of Force and the Permanency of Matter Primary Laws of Nature—Definition of Gravity not according to that Law—Gravity only the Residual Force of a Universal Power—Magnetism of the Ethereal Medium.
Magnetism may be regarded as a new science in consequence of the profound researches and admirable discoveries of Dr. Faraday. Since the magnetism of matter is only known by the action of a magnet or of electricity upon it, by using an extremely energetic magnet or electro-magnet he has proved that all known substances, whether solid, liquid, or aëriform, are more or less magnetic, but that the magnetism is very different in different substances. For example, if a bar of iron be freely suspended between the poles of a very powerful magnet or electro-magnet, it will be attracted by both poles, and will set or rest in the direction of a straight line joining them; but if a similar bar of bismuth be freely suspended in the same manner, it will rest in a direction at right angles to that which the iron bar assumed. Thus the direction in which the iron sets is axial or in the line of force, while that which the bismuth assumes is equatorial or perpendicular to the line of force. Substances that are magnetic after the manner of iron are said to be paramagnetic, those that are magnetic after the manner of bismuth are diamagnetic. As far as we know, all matter comes under one or 336other of these laws. Many bodies are paramagnetic besides iron, as the loadstone, which consists of the peroxide and protoxide of iron mixed with small portions of silica and alumina; also some of the gems and metals, as cobalt, nickel, &c. A substance is often paramagnetic if it contains only the 130,000th part of its weight of iron; but by far the greater number are diamagnetic, as all animal and vegetable matter, acids, oils, sugar, starch, bread, &c., and all the gases except oxygen, which is highly paramagnetic; and its force increases with its density: but notwithstanding the predominance of diamagnetic matter at the surface, the terrestrial globe is paramagnetic—in fact it is a powerful magnet.
Besides the substances which are paramagnetic naturally, that property may be imparted by a variety of methods, as by friction with magnets or even juxtaposition with them; and a bar of hard steel held at the angle of the dip will become a magnet on receiving a few strokes with a hammer on its upper end.
Polarity is one of the most distinguishing characters of magnetism: it is the property which a magnet possesses when freely suspended of resting spontaneously in the magnetic meridian, or nearly north and south, and always returning to that position when disturbed in consequence of the mean magnetic attraction of the earth; yet the magnet has no tendency to move to the north or south even when floating on water, because the same pole that attracts one end repels the other. Both poles of a magnet attract iron, which in return attracts either pole of the magnet with an equal and contrary force. The action of a magnet on unmagnetised iron is confined to attraction, whereas the reciprocal agency of magnets is characterised by a repulsive as well as by an attractive force; for a north pole repels a north pole, and a south pole repels a south pole; but a north and south pole mutually attract one another—which proves that paramagnetism is a dual power in which the conservation of force is perfectly maintained, for the force of attraction is exactly equal to the force of repulsion. One kind of polarity cannot exist without the other: they are absolutely simultaneous, dependent, and of equal intensity.
Induction is the power which a magnet possesses of exciting temporary or permanent paramagnetism in such bodies in its vicinity as are capable of receiving it. By this property the mere approach of a magnet renders iron and steel paramagnetic, 337the more powerfully the less the distance, but the induced force is always exactly equal to the force which produces it. When the north end of a magnet is brought near to, and in the line with, an unmagnetised iron bar, the bar acquires all the properties of a perfect magnet; the end next the north pole of the magnet becomes a south pole, while the remote end becomes a north pole. Exactly the reverse takes place when the south end is presented to the bar, so that each pole of a magnet induces the opposite polarity in the adjacent end of the bar, and the same polarity in the remote extremity; consequently the nearest extremity of the bar is attracted, and the farther repelled; but as the action is greater on the adjacent than on the distant part, the resulting force is that of attraction. By induction the iron bar not only acquires polarity, but the power of inducing paramagnetism in a third body; and although all these properties vanish from the iron as soon as the magnet is removed, a lasting increase of intensity is generally imparted to the magnet itself by the reaction of the temporary paramagnetism of the iron. Iron acquires the inductive force more rapidly than steel, yet it loses it as quickly on the removal of the magnet, whereas the steel is impressed with a lasting polarity.
A certain time is requisite for induction, and it may be accelerated by anything that excites a vibratory motion in the particles of the steel; such as the smart stroke of a hammer, or heat succeeded by sudden cold. A steel bar may be converted into a magnet by the transmission of an electric discharge through it; and as its efficacy is the same in whatever direction the electricity passes, the effect arises from its mechanical operation exciting a vibration among the particles of the steel. It has been observed that the particles of iron easily resume their neutral state after induction, while those of steel resist the restoration of equilibrium, or a return to the neutral state: it is therefore evident that any cause which removes or diminishes the resistance of the particles will tend to destroy the paramagnetism of the steel; consequently the same mechanical means which develop the power will also destroy it. On that account a steel bar may lose its paramagnetism by any mechanical concussion, such as by falling on a hard substance, a blow with a hammer, and heating to redness, which makes the steel soft. The circumstances which determine whether it shall gain or lose are its position with 338respect to the magnetic equator, and the higher or lower intensity of its previous magnetic state.
A comparison of the number of vibrations accomplished by the same magnetised needle during the same time at different distances from a magnet gives the law of paramagnetic intensity, which follows the inverse ratio of the square of the distance—a law that is not affected by the intervention of any substance whatever between the magnet and the needle, provided the substance be not itself susceptible of magnetism. Induction and the reciprocal action of magnets are therefore subject to the laws of mechanics; but the composition and resolution of the forces are complicated in consequence of four forces being constantly in activity, two in each magnet. Mr. Were Fox discovered that the law of the paramagnetic force changes from the inverse square of the distance to the simple inverse ratio when the distance between two magnets is as small as from the fourth to the eighth of an inch, or even as much as half an inch when the magnets are large; and in the case of repulsion, that the change takes place at a still greater distance, especially when the two magnets differ materially in intensity.
Without assuming any hypothesis of what magnetism is, or how that force is originated or sustained, Dr. Faraday regards a magnet as a source of power surrounded by curved lines of force which are not only representants of the magnetic power in quality and direction, but also in quantity—an hypothesis which accords perfectly with experiment, and with the action both of electricity and magnetism. The nature and form of these lines may be seen by placing a bar magnet upon a table, spreading a sheet of stiff paper over it so as to be perfectly level and free from creases, and then sifting very clean iron filings through a fine sieve equably over it. The filings will instantly assume the form of the curved lines represented by fig. 1, plate 7, in consequence of the action of the magnet. These lines are the true representatives of the magnetic forces, and being related to a polar power, they have opposite qualities in opposite directions. When a magnet is broken across the middle, each part is at once converted into a perfect magnet; the part that originally had a south pole acquires a north pole at the fractured end; the part that had originally a north pole gets a south pole; and as far as mechanical division can be carried, it is found that each fragment 339is a perfect magnet. Fig. 2, plate 7, shows the lines of force in a fractured magnet when the ends are not yet separated; fig. 3 shows them when they are.
Currents of electricity are produced in conducting bodies moved across these lines of magnetic force. If a copper wire at a little distance above the north pole of a bar magnet be moved from left to right, at any angle across the lines of magnetic force, they will induce a current of electricity in the wire flowing from right to left; if the wire be moved with the same velocity in the contrary direction, the induced current will be of equal intensity, but it will flow from left to right. Similar results are obtained from the south pole, and the phenomena are the same when the magnet is moved and the wire is at rest; in both cases the intensity is greater the swifter the motion. It appears that the quantity of electricity induced is directly as the amount of the magnetic curves intersected, and when a wire is moving uniformly in a field of equal magnetic force, the current of electricity generated is proportional to the time, and also to the velocity of motion; for when a metallic disc is made to revolve through the lines of force, the current induced is strongest near the edge where the velocity is greatest; and in different substances moving across the lines of force the intensity of the induced current is directly as the conducting power of the substance. Thus bodies moved near a magnet have an electrical current developed in them, and conversely bodies affected by an electric current are definitely moved by a magnet near them.
By the preceding experiments it appears that magnetic polarity is manifested in two ways; in the magnetised needle, by attraction and repulsion, and in a wire moving across lines of magnetic force it is shown by the opposite directions in which the induced current flows according as the body is moved from the right to the left, or left to right. Hence polarity consists in the opposite and antithetical actions manifested at the opposite ends or opposite sides of a limited or unlimited line of force. Antithesis is the true and most general character of magnetism, whatever may be its mode of action.
It was by the induction of electric currents in copper wires moving across the lines of magnetic force that Dr. Faraday proved that the lines of force issuing from a magnet are closed curves which return again and pass through the interior of the 340magnet. He placed two bar magnets of the same length, size, and intensity with their similar poles together, so that they might act as one magnet. A copper wire was then passed between their axes, which after extending through half their length was bent up equatorially and turned back along the outside, so that the whole wire formed a loop, the two ends being connected with a galvanometer. When the whole wire was made to revolve, no effect was produced, although it crossed the lines of magnetic force; but when it was cut in two, so as to separate the external from the internal part, electrical currents of equal intensity, but in contrary directions, were induced in each portion of the wire as they were made separately to cross the lines of force, for the apparatus was so constructed that that could be done. The exterior wire crossed the lines of force which issued from the magnets at right angles to their axes, while the equatorial part of the interior wire traversed the returning lines of force. It is evident that these forces neutralized each other when the whole wire revolved: consequently the internal and external lines of force must have been of equal intensity and opposite in direction, so as to balance one another. By this and a very great number of other experiments Dr. Faraday has proved that the magnetic lines of force are continuous closed curves alike in shape, size, and power. They extend indefinitely beyond the magnet, and undergo no change by distance.
Thus the magnetic force pervades the interior of the mass; if electricity does the same, a compensation must either take place, or it also must move in lines of force, sensible only at the surface. Electricity has a perpetual tendency to escape, and does escape, when not prevented by the coercive power of the air, and other non-conducting substances. Such a tendency does not exist in magnetism, which never leaves the substance containing it under any circumstances whatever. There must be some coercive force, analogous to friction, which arrests the magnetic forces, so as first to oppose their separation, and then to prevent their reunion. In soft iron the coercive force is either wanting or extremely feeble, since iron is easily rendered paramagnetic by induction, and as easily loses that quality; whereas in steel the coercive force is extremely energetic, because it prevents the steel from acquiring the paramagnetic properties rapidly, and entirely hinders it from losing them when acquired. The feebleness of 341the coercive force in iron, and its energy in steel, with regard to the paramagnetic force, is perfectly analogous to the facility of transmission afforded to electricity by non-electrics, and the resistance it experiences in electrics. At every step the analogy between electricity and magnetism becomes more striking. The agency of attraction and repulsion is common to both; the positive and negative electricities are similar to the northern and southern polarities, and are governed by the same laws—namely, that between like powers there is repulsion, and between unlike powers there is attraction. Each of these four forces is capable of acting most energetically when alone; but as the electric equilibrium is restored by the union of the two electric states, and magnetic neutrality by the combination of the two polarities, they respectively neutralise each other when joined. All these forces vary inversely as the square of the distance, and consequently come under the same mechanical laws.
A like analogy extends to magnetic and electric induction. Iron and steel are in a state of equilibrium when neutral; but this equilibrium is immediately disturbed on the approach of the pole of a magnet, which by induction transfers one kind of polarity to one end of an iron or steel bar, and the opposite kind to the other—effects exactly similar to electrical induction. There is even a correspondence between the fracture of a magnet and that of an electric conductor; for if an oblong conductor be electrified by induction, its two extremities will have opposite electricities; and if in that state it be divided across the middle, the two portions, when removed to a distance from one another, will each retain the electricity that has been induced upon it. The analogy, however, does not extend to transference. A body may transfer a redundant quantity of positive electricity to another, or deprive another of its electricity—the one gaining at the expense of the other; but a body cannot possess only one kind of polarity. With that exception, there is such perfect correspondence between the theories of magnetic attractions and repulsions, and electric forces in conducting bodies, that they not only are the same in principle, but are determined by the same formulæ. Experiment concurs with theory in proving the identity of these two influences. Hence, if the electrical phenomena be due to a modification of the ethereal medium, the magnetic phenomena must be owing to an analogous cause.
Curved lines of magnetic force issue from every point of the 342earth’s surface where there is sensible dip, and bending round enter the earth again at the magnetic equator. They induce electric currents in conducting-wires, moving across them exactly the same as in artificial magnets; and when a hollow helix, or coil of copper wire, whose extremities are connected with a galvanometer, is placed in the magnetic dip, and suddenly moved across the lines of force, the needle of the galvanometer will vibrate through an arc of 80° or 90°, in consequence of the electric current induced by these lines of magnetic force in the wire, and the action is greater when a core of soft iron is placed in the helix, which becomes a temporary magnet by induction. Again, if a copper plate be connected with a galvanometer by two copper wires, one from the centre, and another from the circumference, in order to collect and convey the electricity, it is found that, when the plate is made to revolve in a plane passing through the line of the dip, the galvanometer is not affected. But as soon as the plate is inclined to that plane, electricity begins to be developed by its motion across the lines of magnetic force; it becomes more powerful as the inclination increases, and arrives at a maximum when the plate revolves at right angles to the line of dip. When the revolution is in the same direction with that of the hands of a watch, the current of electricity flows from its centre to the circumference; and when the rotation is in a contrary direction, the current sets the opposite way. Thus a copper plate, revolving at right angles to the line of the dip, becomes a new electrical machine, differing from the common plate-glass machine by the copper being the most perfect conductor, whereas glass is the most perfect non-conductor; besides insulation, which is essential to the glass machine, is fatal to the copper one. The quantity of electricity evolved by the metal does not appear to be inferior to that devolved by the glass, though very different in intensity. Even a ship crossing the lines of force must have electric currents running through her. Dr. Faraday observes that such is the facility with which electricity is generated by the magnetic lines of force, that scarcely any piece of metal can be moved without a development of it; consequently, among the arrangements of steam-engines and metallic machinery, curious electro-magnetic combinations probably exist which have never yet been noticed. Thus magnetic lines of force certainly issue from the surface of the globe.
No doubt the earth is a magnet on a vast scale, but it differs 343from all others in having four poles of maximum magnetic force of different intensities, the two in the northern hemisphere having a secular motion in a contrary direction from the two in the southern. They are not even symmetrically placed; hence the magnetic intensity varies so much in the different points on the earth’s surface, that the dynamic equator, or line passing through all the points of least intensity, is a very irregular curve surrounding the globe, but by no means coinciding with the terrestrial equator. In consequence of the mean action of these four forces, the north end of a magnetised needle, arranged so as to revolve in a vertical plane, dips or inclines beneath the horizon in the northern hemisphere, and the south end in the southern. The two hemispheres are separated by a line encircling the earth, called the magnetic equator, or line of no dip, in which the dipping or inclination needle is horizontal. On each side of this line the inclination increases till at last the needle becomes perpendicular to the horizon in two points, or rather small spaces, in each hemisphere, known as the magnetic poles, which are quite different from the poles of the earth’s rotation. The mean action of the four poles of magnetic intensity causes the mariner’s compass, or a magnetic needle suspended so as to revolve in a horizontal plane, to remain at rest when pointing to the two magnetic poles. It is then in the magnetic meridian of the place of observation, which is thus determined by the mean action of all the four magnetic forces.
These mean values of the three magnetic elements, namely, the declination, inclination or dip, and magnetic intensity, are well known to be subject to secular, annual, and diurnal variations. The secular only become sensible after some years, but the annual and diurnal variations have a double progression—that is to say, two maximum and two minimum values in their respective periods of a year and twenty-four hours; for example, the declination needle makes two deviations to the west and two to the east in the course of twenty-four hours, and that with great regularity. Now General Sabine discovered that the double progression arises from two combined or superposed variations having different hours of maxima and minima, and that they are due to two distinctly different causes—the one being the difference in the sun’s position relatively to the place of observation at the different seasons of the year, and hours of the 344day and night; the other being a mean annual and diurnal variation proved by General Sabine to exist in those great magnetic storms or casual disturbances which affect the magnetic elements simultaneously over enormously extensive tracts of the globe.
Moreover the General discovered that, besides these annual and diurnal variations, the magnetic storms have a variation which accomplishes its vicissitudes in ten or more nearly eleven years, the increase from year to year being gradual, till its maximum becomes twice as great as its minimum value. In consequence of this inequality in the storms or casual disturbances, each of the magnetic elements has a variation of similar period and similar maxima and minima. Now the number and magnitude of the spots on the sun had been observed by M. Schwabe, of Dessau, to increase to a maximum, and decrease again to a minimum, regularly in the very same period of between ten and eleven years; and General Sabine found that this variation in the solar spots, and that in the magnetic elements, not only have the same periods of maxima and minima, but that they correspond in all their minutest vicissitudes. Thus a very remarkable and unexpected connexion exists between terrestrial and solar magnetism. The dual and antagonist principle is perfectly maintained in the earth’s magnetism, all the phenomena and their variations being in opposite directions in the two hemispheres. (N. 226.)
No doubt the magnetic lines of force in the earth are closed curves, as in artificial magnets; but in their circuitous courses they may extend to any distance in space, or rather in the ethereal medium, even to thousands or tens of thousands of miles; for the ethereal medium is permeable to lines of magnetic force, or rather transmits them, otherwise the solar spots could not affect the variations of terrestrial magnetism; besides, they pass through the Torricellian vacuum, which is nearly a void with respect to air, but not to the ethereal medium.
The atmosphere which surrounds the earth to the height of about fifty miles with sensible density, consists of three and a half parts by weight of nitrogen gas and one part of oxygen, uniformly mixed. The nitrogen is neutral whether dense or rare, hot or cold, while the oxygen is highly paramagnetic; but it loses a great part of its force when rarefied by heat; consequently 345the magnetic force of the atmosphere must increase from the equator to the poles of maximum cold; it must vary summer and winter, night and day. Its effect upon terrestrial magnetism is unknown; but it can hardly be without some influence. M. E. Becquerel observes—“If we reflect that the earth is encompassed by a mass of air equivalent in weight to a layer of mercury of 30 inches, we may inquire whether such a mass of magnetic gas, continually agitated, and submitted to the regular and irregular variations of pressure and temperature, does not intervene in some of the phenomena dependent upon terrestrial magnetism. If we calculate, in fact, what is the magnetic force of this fluid mass, we find that it is equivalent to an immense plate of iron, of a thickness little more than 1⁄250 of an inch, which covers the whole surface of the globe.” Both the conducting power of the air and its density are increased by cold; and as the sum of the magnetic forces which issue from the earth on one side of the line of no dip is equal to their sum on the other side, the intensity and concentration in our winter are coincident with a diffusion and feebleness in the opposite hemisphere, so that the line of no dip will move annually from north to south and back again. The same holds with regard to day and night. Thus the law of the conservation of force is rigorously maintained; and it is equally so in the effect of the atmosphere on the magnetic lines of force, which refracts them as they pass through it, in one direction in summer, and in the opposite direction in winter—in one direction in the enlightened hemisphere, in the other in that which is dark. The whole of the magnetic lines about the earth are held by their mutual tension in one connected, sensitive system, which feels in every part, even to the antipodes, a change in any particular place.
It may be mentioned as a well-known fact, that apparent anomalies have been found in the diurnal variation of the declination in the high magnetic latitudes of the northern hemisphere when compared with their great regularity in other parts of the same hemisphere, and that the magnetic storms are of much greater magnitude there than in lower latitudes. Moreover, although Captain Maguire’s observations at Cape Barrow, in the North Polar Ocean, show that the annual and diurnal variations of the casual disturbances or magnetic storms, as well as those of the decennial period, are maintained, yet it appears that 346at certain hours of the day the disturbance in the declination may be easterly at Point Barrow, and westerly at the Magnetic Observatory at Toronto, in Upper Canada, and vice versâ: in fact, the magnetic storms are simultaneous at these two stations, but in opposite directions—a circumstance not yet accounted for, and may possibly be due to the increased magnetism of the air in these cold regions. The heat of the sun has no effect upon terrestrial magnetism unless possibly by its indirect action on the oxygen of the atmosphere; but hitherto it has been imperceptible. It is hardly possible that the aurora can be independent of the magnetic character of the air, since it occurs in the high latitudes, where the atmospheric magnetism is most powerful. Captain Maguire remarked that it frequently appeared at Point Barrow when the magnetic storms were at a maximum.
We are totally ignorant of the cause of terrestrial magnetism, though the powerful influence of the solar spots renders it highly probable that it will ultimately be found to originate in the sun himself. Mr. Barlow’s theory of electric currents revolving round the globe is borne out by Mr. Fox’s observations in the Cornish mines, which show that electro-magnetism is extremely active in metallic veins; that not only the nature of the metalliferous deposits must have been determined by their relative electrical conditions, but that the direction of the metallic veins must have been influenced by the direction of the magnetic meridians, and in fact almost all the metallic deposits in the world tend from east to west, or from north-east to south-west. However, these currents of electricity may be regarded as magnetic lines of force, and are more likely to be the effect than the cause of terrestrial magnetism. They are found to have a powerful inductive effect on the Atlantic telegraph, disturbing the needles and galvanometers at each end of the line to a considerable degree, and on the night of the 6th of September, 1858, a magnetic storm passed over the cable, which violently agitated the reflecting galvanometer in connection with the telegraphic wires.
We are equally ignorant of the cause of the secular magnetic variations, but we have no reason to believe that the earth is alone magnetic; on the contrary, the planets are probably magnets, and we know that the sun and moon are magnetic; hence, as the magnetic, like the gravitating force, is transmitted through the ethereal medium, the induction of the sun, moon, 347and planets, in all their secular and periodic changes, may cause perpetual variations in terrestrial magnetism, and it may not be beyond the delicacy of modern observation to ascertain whether a planet, when nearest to the earth, has any sensible magnetism.
Diamagnetism is also a dual power, but in complete antithesis to paramagnetism under the same circumstances. Dr. Faraday first discovered this property in heavy glass, or silico-borate of lead, a piece of which was repelled by the pole of a powerful electro-magnet, and an elongated prism of the same heavy glass, when freely suspended between the poles, set equatorially. He then found that so great a number of substances followed the same law, that it established the very remarkable fact of a hitherto unknown force having acted upon the substances submitted to its influence, a discovery which he subsequently confirmed by many experiments, all of which proved the antithesis between the two modes of magnetic action. He also discovered that magnetic bodies differ exceedingly in their magnetic power: of paramagnetic bodies iron is the most powerful; then follow nickel, cobalt, and a long gradation down to osmium and a vacuum. The body that seems to have the lowest diamagnetic power is arsenic, and the series ascends to heavy glass, antimony, phosphorus, and bismuth; so iron and bismuth are the most powerful in their respective classes, and both have a small conducting power for electricity. It may be presumed that many remarkable instances of diamagnetism are to be met with in nature; among others, Dr. Faraday has suggested the idea that Saturn’s ring, from its position, may be diamagnetic with regard to the planet.
With very powerful magnets or electro-magnets, which are absolutely necessary for all these experiments, it is found that no simple substance is neutral, but that such may be compounded by mixing in due proportion a diamagnetic and paramagnetic liquid, as water and protosulphate of iron.
Professor Tyndall proved diamagnetic polarity by placing two bismuth bars within two vertical coils or spirals of insulated copper wire, through which electric currents were transmitted from a galvanic battery, and caused to act upon a steel magnet freely suspended without the spirals. Now, when the excited magnetism is merely by induction, the electric current, being momentary, only causes a shock or momentary deviation in the 348magnet, which returns to its original position when the current ceases. When, on the contrary, the magnetism is permanent, the suspended magnet does not return to its original position when the current ceases. In Professor Tyndall’s experiment the deviation was permanent, and it was equally so when a bismuth bar was freely suspended and the cores within the spirals were steel magnets. Had the effect been from currents induced in the mass of the bar of bismuth, division of the bar would have stopped them, but the result was the same with powdered bismuth as with the solid mass. Moreover, since the strength of induced currents depends upon the conducting power of the substance, and as the conducting power of copper is forty times as great as that of bismuth, had the polarity been induced and not real, the effect ought to have been forty times greater when copper instead of bismuth cores were put in the spirals, whereas it was scarcely sensible. Besides these proofs, Dr. Tyndall made experiments with eleven different diamagnetic substances, of which water was one, with similar results. He then determined the polarity of twelve paramagnetic bodies by the same method, whence it appeared that the same action which produced a north pole in the paramagnetic bodies produced a south pole in those that were diamagnetic, and vice versâ, whence he concludes that diamagnetic polarity is one of the most firmly established truths of science. It follows from this that, when a man is standing, his head is a north pole and his feet a south, and the top of an iron railing on which he may be leaning is a south pole and the lower end a north. Diamagnetic bodies thus possess a polarity, the same in kind but opposite in direction to that possessed by paramagnetic ones.[18] They are both dual powers, and the two diamagnetic forces like the two paramagnetic being coexistent, simultaneous, and mutually dependent, there can be no doubt that the diamagnetic forces also are represented, or rather consist of curved and closed lines of force passing through the interior of the substance. Dr. Tyndall has proved that the attraction of iron, and the repulsion of bismuth, are as the square of the electro-magnetic current producing them, and that diamagnetic substances are capable of induction.
349The molecular structure of substances freely suspended between the poles of a magnet has a decided effect upon the position they assume.
It has already been mentioned that the optic axis is a symmetrical line in a doubly refracting crystal in which there is no double refraction, and that in some crystals there are two such symmetrical lines. Now, Professor Plücker of Bonn discovered, when such crystals are submitted to powerful magnetic influence, that the single optic axis in the one, and the resultant or mean line between the double optic axes in the other, set diametrically or at right angles to the line of magnetic force; and so powerful did the Professor find the action of magnetism on crystalline form, that the mineral cyanite, when suspended, arranges itself so definitely with regard to terrestrial magnetism, that it might be used as a compass needle.
Dr. Faraday afterwards observed that amorphous substances, cut in the form of a sphere, have no tendency to set or be attracted or repelled in one direction in preference to any other; but if the sphere be formed of a crystallized substance, it is a general fact that, whether it be paramagnetic or diamagnetic, it is more powerfully attracted or repelled in one direction than in any other—a property named by Dr. Faraday magnecrystallic action. For example, a sphere of calcareous spar, which is a diamagnetic crystal, is most strongly repelled in the direction of its principal optic axis, and least strongly in the direction of its least axis. In a sphere of carbonate of iron, which has exactly the same crystalline form and is highly paramagnetic, the line which in carbonate of lime sets equatorially, in this case sets axially, and more strongly in that direction than in any other. The law according to which the attraction of the carbonate of iron increases from the least to its greatest or principal optic axis, is precisely the same as that according to which the repulsion of the calcareous spar increases from the least to the principal optic axis. These relations are not altered by the immersion of the spheres in liquids of either magnetism. Dr. Faraday observed that a line at right angles to the planes of principal cleavage in crystals takes the axial position, and on that account he called it the magnecrystallic axis. Its position was proved by MM. Tyndall and Knoblauch to depend upon the general fact, that the mass is most strongly repelled in the direction of the planes of principal 350cleavage, and that the elective position of crystals depends more upon the direction of these planes with respect to the electric force, than upon the optic axis. The planes of principal cleavage set themselves equatorially in diamagnetic, and axially in paramagnetic substances: it was thence inferred that the phenomena offered by crystals in the magnetic field is a particular case of the general law, that the superior action of magnets upon matter in a particular direction is due to the particles of the body being closer together in that direction than in any other: in short, the line of maximum density; the force exerted being attractive or repulsive according as the particles are paramagnetic or diamagnetic.
It appears, however, that the set of crystals with regard to the line of magnetic force does not depend solely upon their density in particular directions. Professor Matteucci, of Pisa, has proved that the diamagnetic force is inversely as the conducting power of substances for electricity, that the conducting power is a maximum in the planes of principal cleavage, and that a needle of crystallized bismuth, in which the planes of cleavage are parallel to its length, places itself equatorially with more force when these planes are vertical, or at right angles to the force, than when they are horizontal or parallel to it. Experiments had hitherto been made only with diamagnetic or slightly paramagnetic bodies, which induced M. le Roux to try the effect of magnetism on pulverized iron compressed by the hydraulic press, which reduced the grains of iron to lamellæ equivalent to planes of cleavage. Cubes of this substance, suspended by a thread over a horseshoe magnet, oscillated for a longer time when the lamellæ were perpendicular than when they were horizontal; that is, the force was stronger when the lamellæ were equatorial than when they were axial, exactly the same result as in Professor Matteucci’s experiment with the needle of bismuth. Thus the vertical position of the cleavages, which increases the diamagnetism of the bismuth, increases also the paramagnetism of the iron. M. le Roux observes that these results are independent of the influence of the currents of electricity induced in the oscillating body, for the fundamental character of the phenomena of Arago’s discovery of rotation by induction is, that the oscillations diminish rapidly in extent without any sensible diminution in their duration, while in his experiments the time of the oscillations varied. 351He concludes that the arrangement of the molecules must be intimately connected with paramagnetism or diamagnetism itself, since the effect of that arrangement is equally sensible in bismuth and iron, although the diamagnetism of the former is 25,000 times weaker than the paramagnetism of the latter.
The diamagnetism of conducting substances and metals, such as gold, silver, and copper, is augmented by division. Compression has also a great effect on magnetic action. For example, a bar of soft iron sets with its longest dimensions from pole to pole of a magnet, but a bar of compressed carbonate of iron-dust, whose shortest dimensions coincide with the line of pressure, sets equatorially. A bar of bismuth whose plane of principal cleavage is parallel to its length sets equatorially, but a bar of compressed bismuth dust, whose shortest dimensions coincide with the line of pressure, or a bar of bismuth whose principal planes of cleavage are transverse to its length, sets with its length axially. The antithesis is perfect whether the bars are under the influence of a magnet or electro-magnet. For since the diamagnetic force is inversely as the conducting power of a body for electricity, and that the latter is a maximum in the direction of the planes of principal cleavage, therefore when these planes are parallel to the axis of the bismuth bar it sets equatorially; but as the conducting power is augmented when the bismuth dust is compressed in the direction of the force, the diamagnetic power is diminished, and the bar sets axially. Again, since the paramagnetic force augments with the conducting power, the action of the magnet on the iron is antithetic to that on the bismuth.
The action of an electro-magnet on copper is strongly contrasted with that which it exerts on iron or bismuth. For when a copper bar suspended by a thread revolves before its pole, it is brought to a dead halt as soon as the electric current acts upon it, and maintains its position with considerable tenacity, for it does not return when pushed out of it, but keeps its new place with stiffness; however, as soon as the electric current ceases, there is a strong revulsion, the bar revolving the contrary way. Even when swinging with considerable force it may be caught and retained in any position at pleasure, but there is no revulsion when it is arrested either in the axial or equatorial position; at any angle between these two, but especially midway, the electricity will make it move towards the axis, but it is arrested 352before it comes to it. The action depends much on the form and dimensions of the bar and the magnetic pole, which ought to be flat. The phenomena are due to the high electro-conducting power of the copper, and are met with in some of the other pure metals, though in a far inferior degree.
Great magnetic power is requisite for all these experiments. Dr. Faraday employed a magnet that could sustain a weight of 450 lbs. at each pole, and the poles were either pointed or flat surfaces at pleasure, as the kind of experiment required.
Heat strongly affects the magnetic properties of bodies. Dr. Faraday found that, when the temperature of nickel is increased, its magnetic force diminishes; when that of iron is increased its magnetic force remains the same, while that of cobalt increases; which seems to indicate that there is a temperature at which the magnetic force is a maximum, above and below which it diminishes. Nickel loses its magnetism at the temperature of boiling oil, iron at a red heat, and cobalt near the temperature at which copper melts. Calcareous spar retains its magnetic character at a very high temperature; but the same substance when it contains iron, and also oxide of iron, loses it entirely at a dull red heat. A crystal of the ferrocarbonate of lime was absolutely reversed by change of temperature, for at a low heat the optic axis pointed axially, and at a high temperature equatorially. With the exception of these substances, magnecrystals, whether paramagnetic or diamagnetic, are generally all affected alike by heat. The difference between the forces in any two different directions, as for instance the greatest and least principal axes, diminishes as the temperature is raised, increases as the temperature is lowered, and is constant for a given temperature. No unmixed or pure substance has as yet passed by heat from the paramagnetic to the diamagnetic state. No simple magnecrystal has shown any inversion of this kind, nor have any of the chief axes of power changed their characters or relations to one another.
It appears that, as the molecules of crystals and compressed bodies affect magnetism, so magnetism acts upon the molecules of matter, for torsion diminishes the magnetic force, and the elasticity of iron and steel is altered by magnetism. M. Matteucci has found that the mechanical compression of glass alters the rotatory power of a polarized ray of light transmitted through it, and that 353a change takes place in the temper of glass under the influence of powerful magnetism.
Even from the limited view of the powers of nature which precedes, it is evident that the progress of science based upon experiment tends to show that the various forces of light, heat, motion, chemical affinity, electricity, and magnetism will ultimately be traced to one common origin; that they are so directly related, and mutually dependent, that they are convertible, motion producing heat, and heat motion; chemical affinity producing electricity, and electricity chemical action, &c., each mediately or immediately producing the other. These forces are transmitted through substances; they act upon matter, causing changes in the molecular structure of bodies either momentary or permanent, and reciprocally the changes indicate the action of these forces. Matter and force are only known to us as manifestations of Almighty power: we are assured that we can neither create nor destroy them—that their amount is the same now as in the beginning. In chemical attraction the powers with which a molecule of matter is endowed, and which give rise to various qualities, never change; even when passing through a thousand combinations, the molecule and its power are ever the same.
Machinery does not create force; it only enables us to turn the forces of nature to the best advantage; it is by the force of wind or falling water that our corn is ground, and the steam engine owes its power to the force of heat and chemical action. As force cannot be created, neither can it be annihilated. It may be dispersed in various directions, and subdivided so as to become evanescent to our perceptions; it may be balanced so as to be in abeyance, or become potential as in static electricity; but the instant the impediment is removed the force is manifested by motion; it may also be turned into heat by friction, but it is never lost. Every motion we make, every breath, every word we utter, is a force that produces pulsations which are communicated to continually increasing particles of air, and conveyed through countless channels so as to become indeed imperceptible to our senses, yet they are demonstrated to exist as witnesses of the words we have spoken or the actions we have performed, by analysis, that all-powerful instrument of human reason.[19]
354A body acquires heat in the exact proportion that the adjacent substances become cold, and when heat is absorbed by a body it becomes an expansive force at the expense of those around that contract, but it is not lost. In chemical action at a distance the principle of the conservation of force is maintained, for a chemical action may be produced miles away from an electro-magnet, perfectly equivalent to the dominant chemical action in the battery. The two electricities are developed in equal proportions, which may be combined so as to produce many changes in their respective relations, yet the sum of the force of one kind can never be made in the smallest degree either to exceed or to come short of the sum of the other. Experimental research proves that the conservation of force is an unalterable law of nature—“a principle in physics as large and sure as that of the indestructibility of matter or the invariability of gravity. No hypothesis should be admitted, nor any assertion of a fact credited, that denies this principle. No view should be inconsistent or incompatible with it. Many of our hypotheses in the present state of science may not comprehend it, and may be unable to suggest its consequences, but none should oppose or contradict it.”
Having thus expressed his conviction of the truth of this great principle, Dr. Faraday considers the case of gravity, and concludes that “the definition of gravity as an attractive force between the particles of matter varying inversely as the square of the distance, while it stands as a full definition of the power, is inconsistent with the principle of the conservation of force.” For while in this definition the principle is maintained of the constancy of the force at the same distance, it implies a creation of force to an enormous amount when the distance is diminished, and an equal amount annihilated when the distance is increased,—“an effect,” he says, “which is equal in its infinity and its consequences with creation, and only within the power of Him who creates.” He continues, “It will not be imagined for a moment that I am opposed to what may be called the law of gravitating action, that is, the law by which all the known effects of gravity are governed; what I am considering is the definition of the force of gravitation. That the result of one exercise of a power may be inversely as the square of the distance, I believe and admit; and I know that it is so in the case of gravity, and has been verified to an extent that could hardly 355have been within the conception of Newton himself when he gave utterance to the law; but that the totality of a force can be employed according to that law I do not believe either in relation to gravitation, or electricity, or magnetism, or any other supposed form of power. That there should be a power of gravitation existing by itself, having no relation to the other natural powers, and no respect to the law of the conservation of force, is as little likely as that there should be a principle of levity as well as gravity. Gravity may be only the residual part of the other forces of nature, as Mossotti has tried to show; but that it should fall out from the law of all other forces, and should be outside the reach either of farther experiment or philosophical conclusions, is not probable. So we must strive to learn more of this outstanding power, and endeavour to avoid any definition of it which is incompatible with the principles of force generally, for all the phenomena of nature lead us to believe that the great and governing law is one. Thus gravitation can only be considered as part of a more general force whose law has yet to be discovered.”
The definition of the gravitating force immediately suggests the question of how it is transmitted; the full force of that question was felt by Newton himself when, in his third letter to Bentley, he wrote, “That gravity should be innate, inherent, and essential to matter, so that one body may act upon another at a distance, through a vacuum, without the mediation of anything else by and through which their action and force may be conveyed from one to another, is to me so great an absurdity that I believe no man who has in philosophic matters a competent faculty of thinking can ever fall into it. Gravity must be caused by an agent, acting constantly according to certain laws; but whether this agent be material or immaterial I have left to the consideration of my readers.”
Since Newton’s time the continual decrease in the periodic times of the comets belonging to our system, and the undulatory theory of light and heat, have proved the existence of an extremely rare elastic medium filling space even to the most distant regions of which we are cognizant. But, rare as it may be, it has inertia enough to resist the motion of comets, and therefore must be material, whether considered to be ether or, according to Mr. Grove, the highly attenuated atmospheres of the celestial bodies. 356Professor William Thomson of Glasgow has computed that in the space traversed by the earth in its annual revolution, a cube whose side is 1000 miles would contain not less than a pound weight of the ethereal medium, and that the earth, in moving through it, would not displace the ·250th part of that pound of matter. Yet that is enormously more dense than the continuation of the earth’s atmosphere would be in interplanetary space, if rarefied according to Bayle’s law. But whatever be the density or nature of the ether, there is every reason to believe that it is the medium which transmits the gravitating force from one celestial object to another, or possibly it may possess a higher attribute with regard to gravity than its mere transmission.
Dr. Faraday, who discovered the magnetism of the atmosphere, is led to believe that the ethereal medium too is magnetic by the following experiment. Three solutions of the protosulphate of iron, l, m, n, the first of which contained 4 grains of the salt dissolved in a cubic inch of water, the second 8 grains, and the third 16 grains—these were respectively enclosed in three glass globules, all of which were attracted by the pole of a magnet. A quantity of the mean solution m was then put into a vessel, and the globule containing the strongest solution n was immersed in it, which was attracted as before, but the globule l, containing the weakest solution, was repelled when plunged into the same liquid. Here there was a diamagnetic phenomenon, although the glass globules and the liquid in which they were immersed contained iron. The effect was evidently differential, for when the liquid was less attracted than the globule, the globule approached the pole, and when the liquid was more attracted than the globule, the latter appeared to recede from the pole. In fact, the effect is the same as that of gravity on a body immersed in water; if it be more forcibly attracted than the water, it sinks; if less forcibly attracted, it rises, the effect being the same as if it were repelled by the earth. Hence the question, are all magnetic phenomena the result of a differential action of this kind, and is the ethereal medium less strongly attracted than soft iron, and more strongly attracted than bismuth, thus permitting the approach of the iron, but causing the bismuth to recede from the pole of a magnet? If such a medium exist, that is, if the ethereal medium be magnetic, then diamagnetism is 357the same with paramagnetism, and the polarity of the magnetic force in iron and bismuth is one and the same.
The ethereal medium may be presumed to transmit the gravitating force; it transmits the magnetism of the solar spots, its undulations constitute light, heat, and all the influences bound up in the solar beam; and the most perfect vacuum we can make is capable of transmitting mechanical energy in enormous quantities, some of which differ but little from that of air or oxygen at an ordinary barometric pressure; and why not thus admit, says Mr. Thomson, the magnetic property, of which we know so little that we have no right to pronounce a negative?
Mr. Waterstone is also of opinion that it would be taking too narrow a view if we limited the function of the luminiferous ether to the conveying of physical pulses only. The atmosphere also conveys physical pulses, but that is the least important of its functions in the economy of nature. There is nothing that should hinder us attributing to the media concerned in the radiation of light and heat the higher functions of electrical polarity and gravitation. The special dynamic arrangements by which this is effected may ever elude our research; but as there is no limit to the vis viva (N. 222) which such media may conserve in their minutest parts, so there is no physical impossibility in that vis viva being suddenly transferred to the molecules of ordinary matter in the proportion and sequence required to carry out the order and system of nature.
The fundamental principle of action in such media must be in accordance with elastic impact, for upon that the dynamic theory of heat and conservation of force rests as a foundation. The statical and dynamical characteristics of gravitation and transfusion of force conform to it, so that all the forces that hold the molecules of bodies together must also be in subjection to it.[20]
Ethereal Medium—Comets—Do not disturb the Solar System—Their Orbits and Disturbances—M. Faye’s Comet probably the same with Lexel’s—Periods of other three known—Acceleration in the mean Motions of Encke’s and Biela’s Comets—The Shock of a Comet—Disturbing Action of the Earth and Planets on Encke’s and Biela’s Comets—Velocity of Comets—The Comet of 1264—The great Comet of 1343—Physical Constitution—Shine by borrowed Light—Estimation of their Number.
In considering the constitution of the earth, and the fluids which surround it, various subjects have presented themselves to our notice, of which some, for aught we know, are confined to the planet we inhabit; some are common to it and to the other bodies of our system. But an all-pervading ether must fill the whole visible creation, since it conveys, in the form of light, tremors which may have been excited in the deepest recesses of the universe thousands of years before we were called into being. The existence of such a medium, though at first hypothetical, is proved by the undulatory theory of light, and rendered certain by the motion of comets, and by its action upon the vapours of which they are chiefly composed. It has often been imagined that the tails of comets have infused new substances into our atmosphere. Possibly the earth may attract some of that nebulous matter, since the vapours raised by the sun’s heat, when the comets are in perihelio, and which form their tails, are scattered through space in their passage to their aphelion; but it has hitherto produced no effect, nor have the seasons ever been influenced by these bodies. The light of the comet of the year 1811, which was so brilliant, did not impart any heat even when condensed on the bulb of a thermometer of a structure so delicate that it would have made the hundredth part of a degree evident. In all probability, the tails of comets may have passed over the earth without its inhabitants being conscious of their presence; and there is reason to believe that the tail of the great comet of 1843 did so. M. Valz observed that the light of a brilliant 359comet was eclipsed as it passed over a star of the 7th magnitude, whence M. Babinet computed that the light of the comet must have been sixty times less than that of the star, and that matter so attenuated could not penetrate the earth’s atmosphere, but the constitution of these bodies is still a matter of conjecture.
The passage of comets has never sensibly disturbed the stability of the solar system; their nucleus, being in general only a mass of vapour, is so rare, and their transit so rapid, even when they had a solid part, that the time has not been long enough to admit of a sufficient accumulation of impetus to produce a perceptible action. Indeed, M. Dusejour has shown that, under the most favourable circumstances, a comet cannot remain longer than two hours and a half at a less distance from the earth than 10,500 leagues. The comet of 1770 passed within about six times the distance of the moon from the earth, without even affecting our tides. According to La Place, the action of the earth on the comet of 1770 augmented the period of its revolution by more than two days; and, if comets had any perceptible disturbing energy, the reaction of the comet ought to have increased the length of our year. Had the mass of that comet been equal to the mass of the earth, its disturbing action would have increased the length of the sidereal year by 2h 53m; but, as Delambre’s computations from the Greenwich observations of the sun show that the length of the year has not been increased by the fraction of a second, its mass could not have been equal to the 1⁄5000th part of that of the earth. This accounts for the same comet having twice swept through the system of Jupiter’s satellites without deranging the motion of these moons. M. Dusejour has computed that a comet, equal in mass to the earth, passing at the distance of 12,150 leagues from our planet, would increase the length of the year to 367d 16h 5m, and the obliquity of the ecliptic as much as 2°. So the principal action of comets would be to alter the calendar, even if they were dense enough to affect the earth.
Comets traverse all parts of the heavens; their paths have every possible inclination to the plane of the ecliptic, and, unlike the planets, the motion of more than half of those that have appeared has been retrograde, that is, from east to west. They are only visible when near their perihelia; then their velocity is such, that its square is twice as great as that of a body moving in a circle at the same distance: they consequently remain but a 360very short time within the planetary orbits. And, as all the conic sections of the same focal distance sensibly coincide, through a small arc, on each side of the extremity of their axis, it is difficult to ascertain in which of these curves the comets move, from observations made, as they necessarily must be, near their perihelia (N. 227). Probably they all move in extremely excentric ellipses; although, in most cases, the parabolic curve coincides most nearly with their observed motions. Some few seem to describe hyperbolas; such, being once visible to us, would vanish for ever, to wander through boundless space, to the remote systems of the universe. If a planet be supposed to revolve in a circular orbit, whose radius is equal to the perihelion distance of a comet moving in a parabola, the areas described by these two bodies in the same time will be as unity to the square root of two, which forms such a connexion between the motion of comets and planets, that, by Kepler’s law, the ratio of the areas described during the same time by the comet and the earth may be found; so that the place of a comet may be computed at any time in its parabolic orbit, estimated from the instant of its passage at the perihelion. It is a problem of very great difficulty to determine all the other elements of parabolic motion—namely, the comet’s perihelion distance, or shortest distance from the sun, estimated in parts of the mean distance of the earth from the sun; the longitude of the perihelion; the inclination of the orbit on the plane of the ecliptic; and the longitude of the ascending node. Three observed longitudes and latitudes of a comet are sufficient for computing the approximate values of these quantities; but an accurate estimation of them can only be obtained by successive corrections, from a number of observations, distant from one another. When the motion of a comet is retrograde, the place of the ascending node is exactly opposite to what it is when the motion is direct. Hence the place of the ascending node, together with the direction of the comet’s motion, show whether the inclination of the orbit is on the north or south side of the plane of the ecliptic. If the motion be direct, the inclination is on the north side; if retrograde, it is on the south side.
The identity of the elements is the only proof of the return of a comet to our system. Should the elements of a new comet be the same, or nearly the same, with those of any one previously known, the probability of the identity of the two bodies is very 361great, since the similarity extends to no less than four elements, every one of which is capable of an infinity of variations. But, even if the orbit be determined with all the accuracy the case admits of, it may be difficult, or even impossible, to recognize a comet on its return, because its orbit would be very much changed if it passed near any of the large planets of this or of any other system, in consequence of their disturbing energy, which would be very great on bodies of so rare a nature.
By far the most curious and interesting instance of the disturbing action of the great bodies of our system is found in the comet of 1770. The elements of its orbit, determined by Messier, did not agree with those of any comet that had hitherto been computed, yet Lexel ascertained that it described an ellipse about the sun, whose major axis was only equal to three times the length of the diameter of the terrestrial orbit, and consequently that it must return to the sun at intervals of five years and a half. This result was confirmed by numerous observations, as the comet was visible through an arc of 170°; yet this comet had never been observed before the year 1770, nor has it ever again been seen till 1843, though very brilliant. The disturbing action of the larger planets affords a solution of this anomaly, as Lexel ascertained that in 1767 the comet must have passed Jupiter at a distance less than the fifty-eighth part of its distance from the sun, and that in 1779 it would be 500 times nearer Jupiter than the sun; consequently the action of the sun on the comet would not be the fiftieth part of what it would experience from Jupiter, so that Jupiter became the primum mobile. Assuming the orbit to be such as Lexel had determined in 1770, La Place found that the action of Jupiter, previous to the year 1770, had so completely changed the form of it, that the comet which had been invisible to us before 1770 was then brought into view, and that the action of the same planet, producing a contrary effect, has subsequently to that year removed it from our sight, since it was computed to be revolving in an orbit whose perihelion was beyond the orbit of Ceres. However, the action of Jupiter during the summer of 1840 must have been so great, from his proximity to that singular body, that he seems to have brought it back to its former path as he had done in 1767, for the elements of the orbit of a comet which was discovered in November 1843, by M. Faye, agree so nearly with those of the orbit of Lexel’s comet 362that the two bodies were supposed to be identical; by the subsequent computation of M. le Verrier, it appears, however, that they are not the same, that they were both brought to our system by Jupiter’s attraction, and that they have been in it more than a century, and have frequently come near the earth without having been seen. From the smallness of the excentricity of Lexel’s comet, the orbit resembles those of the planets, but this comet is liable to greater perturbations than any other body in the system, because it comes very near the orbit of Mars when in perihelion, and very near that of Jupiter when in aphelion; besides, it passes within a comparatively small distance of the orbits of the minor planets; and as it will continue to cross the orbit of Jupiter at each revolution till the two bodies meet, its periodic time, now about seven years, will again be changed, but in the mean time it ought to have returned to its perihelion in the year 1851. This comet might have been seen from the earth in 1776, had its light not been eclipsed by that of the sun. There is still so much doubt with regard to Lexel’s comet that during the present year, 1858, M. le Verrier has constructed a table of all the orbits in which the comet may have moved after leaving Jupiter in 1770, which will enable astronomers to recognise the comet even should the elements of its orbit be much altered. He thinks it possible that its path may have become hyperbolic, but that it is more likely an augmentation of its periodic time may have taken place. It is quite possible that comets frequenting our system may be turned away, or others brought to the sun, by the attraction of planets revolving beyond the orbit of Neptune, or by bodies still farther removed from the solar influence.
Other comets, liable to less disturbance, return to the sun at stated intervals. Halley computed the elements of the orbit of a comet that appeared in the year 1682, which agreed so nearly with those of the comets of 1607 and 1531, that he concluded it to be the same body returning to the sun at intervals of about seventy-five years. He consequently predicted its reappearance in the year 1758, or in the beginning of 1759. Science was not sufficiently advanced in the time of Halley to enable him to determine the perturbations this comet might experience; but Clairaut computed that, in consequence of the attraction of Jupiter and Saturn, its periodic time would be so much shorter than during its revolution between 1607 and 1682, 363that it would pass its perihelion on the 18th of April, 1759. The comet did arrive at that point of its orbit on the 12th of March, which was thirty-seven days before the time assigned. Clairaut subsequently reduced the error to twenty-three days; and La Place has since shown that it would only have been thirteen days if the mass of Saturn had been as well known as it is now. It appears, from this, that the path of the comet was not quite known at that period; and, although many observations were then made, they were far from attaining the accuracy of those of the present day. Besides, since the year 1759, the orbit of the comet has been altered by the attraction of Jupiter in one direction, and that of Saturn, Uranus, and Neptune in the other; yet, notwithstanding these sources of uncertainty, and our ignorance of all the possible causes of derangement from unknown bodies on the confines of our system, or in the regions beyond it, the comet appeared exactly at the time, and not far from the place assigned to it by astronomers; and its actual arrival at its perihelion a little before noon on the 16th of November, 1835, only differed from the computed time by a very few days, which was probably owing to the attraction of Neptune.
The fulfilment of this astronomical prediction is truly wonderful, if it be considered that the comet is seen only for a few weeks during its passage through our system, and that it wanders from the sun for seventy-five years to twice the distance of Uranus. This enormous orbit is four times longer than it is broad; its length is about 3420 millions of miles, or about thirty-six times the mean distance of the earth from the sun. At its perihelion the comet comes within nearly fifty-seven millions of miles of the sun, and at its aphelion it is sixty times more distant. On account of this extensive range it must experience 3600 times more light and heat when nearest to the sun than in the most remote point of its orbit. In the one position the sun will seem to be four times larger than he appears to us, and at the other he will not be apparently larger than a star (N. 228.)
On the first appearance of Halley’s comet, early in August 1835, it seemed to be merely a globular mass of dim vapour, without a tail. A concentration of light, a little on one side of the centre, increased as the comet approached the sun and earth, and latterly looked so like the disc of a small planet, that it 364might have been mistaken for a solid nucleus. M. Struve, however, saw a central occultation of a star of the ninth magnitude by the comet, at Dorpat, on the 29th of September. The star remained constantly visible, without any considerable diminution of light; and, instead of being eclipsed, the nucleus of the comet disappeared at the moment of conjunction from the brilliancy of the star. The tail increased as the comet approached its perihelion, and shortly before it was lost in the sun’s rays it was between thirty and forty degrees in length.
According to the observations of M. Valz, the nebulosity increased in magnitude as it approached the sun; but no other comet on record has exhibited such sudden and unaccountable changes of aspect. It was invisible for two months when near its perihelion passage, and when it reappeared on the 24th of January, 1836, its aspect was completely changed; it had no tail, and to the naked eye was like a hazy star; but with a powerful telescope it presented a small, round, planetary-looking nucleus 2ʺ in diameter, surrounded by an extensive coma, and in the centre it had a small, bright, solid part. The nucleus, clear and well defined, like the disc of a planet, was observed on one occasion to become obscure and enlarged in the course of a few hours. But by far the most remarkable circumstance was the sudden appearance of certain luminous brushes or sectors, diverging from the centre of the nucleus through the nebulosity. M. Struve describes the nucleus of the comet, in the beginning of October, as elliptical, and like a burning coal, out of which there issued, in a direction nearly opposite to the tail, a divergent flame, varying in intensity, form, and direction, appearing occasionally even double, and suggesting the idea of luminous gas bursting from the nucleus. On one occasion M. Arago saw three of these divergent flames on the side opposite the tail, rising through the nebulosity, which they greatly exceeded in brilliancy: after the comet had passed its perihelion, it acquired another of these luminous fans, which was observed by Sir John Herschel at the Cape of Good Hope. Hevelius describes an appearance precisely similar, which he had witnessed in this comet at its approach to the sun in the year 1682, and something of the kind seems to have been noticed in the comet of 1744. Possibly the second tail of the comet of 1724, which was directed towards the sun, may have been of this nature.
365The influence of the ethereal medium on the motions of Halley’s comet will be known after another revolution, and future astronomers will learn, by the accuracy of its returns, whether it has met with any unknown cause of disturbance in its distant journey. Undiscovered planets, beyond the visible boundary of our system, may change its path and the period of its revolution, and thus may indirectly reveal to us their existence, and even their physical nature and orbit. The secrets of the yet more distant heavens may be disclosed to future generations by comets which penetrate still farther into space, such as that of 1763, which, if any faith may be placed in the computation, goes nearly forty-three times farther from the sun than Halley’s does, and shows that the sun’s attraction is powerful enough, at the enormous distance of 15,500 millions of miles, to recall the comet to its perihelion. The periods of some comets are said to be of many thousand years, and even the average time of the revolution of comets generally is about a thousand years; which proves that the sun’s gravitating force extends very far. La Place estimates that the solar attraction is felt throughout a sphere whose radius is a hundred millions of times greater than the distance of the earth from the sun.
Authentic records of Halley’s comet do not extend beyond the year 1456, yet it may be traced, with some degree of probability, even to a period preceding the Christian era. But as the evidence only rests upon coincidences of its periodic time, which may vary as much as eighteen months from the disturbing action of the planets, its identity with comets of such remote times must be regarded as extremely doubtful.
This is the first comet whose periodicity has been established. It is also the first whose elements have been determined from observations made in Europe; for, although the comets which appeared in the years 240, 539, 565, and 837, are the most ancient of those whose orbits have been traced, their elements were computed from Chinese observations.
Besides Halley’s and Lexel’s comets, ten or twelve others are now known to form part of the solar system; that is to say, they return to the sun at stated periods. Six of them have periods of less than eight years. That generally called Encke’s comet, or the comet of the short period, was first seen by MM. Messier and Mechain in 1786, again by Miss Herschel in 1805, and its returns, 366in the years 1805 and 1819, were observed by other astronomers, under the impression that all four were different bodies. However, Professor Encke not only proved their identity, but determined the circumstances of the comet’s motion. Its reappearance in the years 1825, 1828, and 1832, accorded with the orbit assigned by M. Encke, who thus established the length of its period to be 1204 days, nearly. This comet is very small, of feeble light, and invisible to the naked eye, except under very favourable circumstances, and in particular positions. It has no tail, it revolves in an ellipse of great excentricity inclined at an angle of 13° 22ʹ to the plane of the ecliptic, and is subject to considerable perturbations from the attraction of the planets, which occasion variations in its periodic time. Among the many perturbations to which the planets are liable, their mean motions, and therefore the major axes of their orbits, experience no change; while, on the contrary, the mean motion of the moon is accelerated from age to age—a circumstance at first attributed to the resistance of an ethereal medium pervading space, but subsequently proved to arise from the secular diminution of the excentricity of the terrestrial orbit. Although the resistance of such a medium has not hitherto been perceived in the motions of such dense bodies as the planets and satellites, its effects on the revolutions of the comets leave no doubt of its existence. From the numerous observations that have been made on each return of the comet of the short period, the elements have been computed with great accuracy on the hypothesis of its moving in vacuo. Its perturbations occasioned by the disturbing action of the planets have been determined; and, after everything that could influence its motion had been duly considered, M. Encke found that an acceleration of about two days in each revolution has taken place in its mean motion, precisely similar to that which would be occasioned by the resistance of an ethereal medium. And, as it cannot be attributed to a cause like that which produces the acceleration of the moon, it must be concluded that the celestial bodies do not perform their revolutions in an absolute void, and that, although the medium be too rare to have a sensible effect on the masses of the planets and satellites, it nevertheless has a considerable influence on so rare a body as a comet. Contradictory as it may seem that the motion of a body should be accelerated by the resistance of an ethereal medium, the truth 367becomes evident if it be considered that both planets and comets are retained in their orbits by two forces which exactly balance one another; namely, the centrifugal force producing the velocity in the tangent, and the attraction of the gravitating force directed to the centre of the sun. If one of these forces be diminished by any cause, the other will be proportionally increased. Now, the necessary effect of a resisting medium is to diminish the tangential velocity, so that the balance is destroyed, gravity preponderates, the body descends towards the sun till equilibrium is again restored between the two forces; and, as it then describes a smaller orbit, it moves with increased velocity. Thus, the resistance of an ethereal medium actually accelerates the motion of a body; but, as the resisting force is confined to the plane of the orbit, it has no influence whatever on the inclination of the orbit, or on the place of the nodes. In computing its effect, M. Encke assumed the increase to be inversely as the square of the distance, and that its resistance acts as a tangential force proportional to the squares of the comet’s actual velocity in each point of its orbit. Another comet belonging to our system, which returns to its perihelion after a period of 63⁄4 years, has been accelerated in its motion by a whole day during one revolution, which puts the existence of ether beyond a doubt, and confirms the undulatory theory of light. Since this comet, which revolves nearly between the orbits of the earth and Jupiter, is only accelerated one day at each revolution, while Encke’s, revolving nearly between the orbits of Mercury and Pallas, is accelerated two, the ethereal medium must increase in density towards the sun. The comet in question was discovered by M. Biela at Josephstadt on the 27th of February, 1826, and ten days afterwards it was seen by M. Gambart at Marseilles, who computed its parabolic elements, and found that they agreed with those of the comets which had appeared in the years 1789 and 1795, whence he concluded them to be the same body moving in an ellipse, and accomplishing its revolution in 2460 days. The perturbations of this comet were computed by M. Damoiseau, who predicted that it would cross the plane of the ecliptic on the 29th of October, 1832, a little before midnight, at a point nearly 18,484 miles within the earth’s orbit; and as M. Olbers of Bremen, in 1805, had determined the radius of the comet’s head to be about 21,136 miles, it was evident that its nebulosity would 368envelop a portion of the earth’s orbit,—a circumstance which caused some alarm in France, from the notion that, if any disturbing cause had delayed the arrival of the comet for one month, the earth must have passed through its head. M. Arago dispelled these fears by his excellent treatise on comets, in the Annuaire of 1832, where he proves that, as the earth would never be nearer the comet than 18,000,000 British leagues, there could be no danger of collision. The earth is in more danger from these two small comets than from any other. Encke’s crosses the terrestrial orbit sixty times in a century, and may ultimately come into collision, but both are so extremely rare, that little injury is to be apprehended.
The earth would fall to the sun in 641⁄2 days, if it were struck by a comet with sufficient impetus to destroy its centrifugal force. What the earth’s primitive velocity may have been it is impossible to say. Therefore a comet may have given it a shock without changing the axis of rotation, but only destroying part of its tangential velocity, so as to diminish the size of the orbit—a thing by no means impossible, though highly improbable. At all events, there is no proof of this having occurred; and it is manifest that the axis of the earth’s rotation has not been changed, because, as the ether offers no sensible resistance to so dense a body as the earth, the libration would to this day be evident in the variation it must have occasioned in the terrestrial latitudes. Supposing the nucleus of a comet to have a diameter only equal to the fourth part of that of the earth, and that its perihelion is nearer to the sun than we are ourselves, its orbit being otherwise unknown, M. Arago has computed that the probability of the earth receiving a shock from it is only one in 281 millions, and that the chance of our coming in contact with its nebulosity is about ten or twelve times greater. Only comets with retrograde motions can come into direct collision with the earth, and if the momentum were great the event might be fatal; but in general the substance of comets is so rare, that it is likely they would not do much harm if they were to impinge; and even then the mischief would probably be local, and the equilibrium soon restored, provided the nucleus were gaseous, or very small. It is, however, more probable that the earth would only be deflected a little from its course by the approach of a comet, without being touched by it. The comets that have come nearest to the earth 369were that of the year 837, which remained four days within less than 1,240,000 leagues from our orbit: that of 1770, which approached within about six times the distance of the moon. The celebrated comet of 1680 also came very near to us; and the comet whose period is 63⁄4 years was ten times nearer the earth in 1805 than in 1832, when it caused so much alarm.
Encke’s and Biela’s comets are at present far removed from the influence of Jupiter, but they will not always remain so, because, the aphelia and nodes of the orbits of these two comets being the points which approach nearest to the orbit of Jupiter at each meeting of the planet and comets, the major axis of Encke’s comet will be increased and that of Biela’s diminished, till in the course of time, when the proximity has increased sufficiently, the orbits will be completely changed, as that of Lexel’s was in 1770. Every twenty-third year, or after seven revolutions of Encke’s comet, its greatest proximity to Jupiter takes place, and at that time his attraction increases the period of its revolution by nine days—a circumstance which took place in the end of the years 1820 and 1843. But from the position of the bodies there is a diminution of three days in the six following revolutions, which reduces the increase to six days in seven revolutions. Thus, before the year 1819, the periodic time of Encke’s comet was 1204 days, and it was 1219 days in accomplishing the revolution that ended in 1845. By this progressive increase the orbit of the comet will reach that of Jupiter in seven or eight centuries, and then by the very near approach of the two bodies it will be completely changed.
At present the Earth and Mercury have the most powerful influence on the motions of Encke’s and Biela’s comets; and have had for so long a time that, according to the computation of Mr. Airy, the present orbit of the latter was formed by the attraction of the Earth, and that of Encke’s by the action of Mercury. With regard to the latter comet, that event must have taken place in February 1776. In 1786 Encke’s comet had both a tail and a nucleus, now it has neither; a singular instance of the possibility of their disappearance. It was in perihelio in 1855.
In 1846 Biela’s comet was divided into two distinct bodies, by what strange accident is altogether a mystery. The nuclei 370of the two comets were separated by about 150,000 miles, and they travelled together with their tails parallel, and an arch of light over their heads. Till that time Biela’s comet never had been seen with a tail. The new head was dull at first, but increased in size and brightness till it surpassed its companion in both; besides, it had a bright flashing diamond-like point in its centre—gradually it resumed its dull appearance, and its period was computed to be eight days longer than that of the original head. They had separated to a greater distance from one another in 1853, but were still travelling together, one having become smaller than the other.
A comet discovered by M. Brorsen of Kiel, on the 26th of February, 1846, came, on the 20th of April following, nearly as close to Jupiter as his fourth satellite, when Jupiter’s attraction must have been ten times greater than that of the sun; so there is every reason to believe that the comet’s orbit will be as much altered as that of Lexel’s; and another discovered by Padre de Vico at Rome, on the 22nd of August, will, in all probability, be as much disturbed by the same cause. One of the comets found by that astronomer has a period which varies, according to different computations, from 55 to 99 years; it certainly has an elliptical orbit. That discovered at Naples by Mr. Peters revolves about the sun in 16 years; but Olbers’s comet of 1815 must go nearly the same distance into space with Halley’s, since its period is 74 years. Two discovered by M. Brorsen have periods, one of 500 and the other of 28 years; but of the latter there is some uncertainty.
The comet which appeared in 1596 and 1845 has a period of 249 years; and should M. Argelander’s computation be accurate, the orbit which has hitherto been assigned to the great comet of 1811 must be erroneous, since he has ascertained its period to be 3066 years.
The great comet of 1264, which had a tail that extended over 100° of the celestial vault, was observed and recorded by the Chinese, and was ascertained to be the same that had appeared in 1556, and of whose motions observations were taken at Vienna in the reign of the Emperor Charles V., but it was then less brilliant. In consequence of the discovery of the original observations of the comet of 1556, by Fabricius at Vienna, and by Heller at Nuremburg, Mr. Hind was induced to compute its 371orbit for that year; but after much labour, aided by all the improved methods of calculation, he found Heller’s observations so confused, and even erroneous, that he could not determine the curve described by the comet at that time with any precision, and therefore could only predict that the epoch of its return would be some time between 1848 and 1861. Before comets reach the sun they are rarely conspicuous; but if after passing their perihelion they come near the earth, then they have tails, and become brilliant in consequence of the sun’s action upon the matter of which they are formed. Now if the comet in question should pass its perihelion between the months of March and October, it possibly may be as remarkable as ever; but should it come nearest to the sun in winter, such is the position of its orbit with regard to the earth, that it may pass unnoticed—which is very unlikely, as search is being made for it at almost all the observatories in Europe and in the United States. Nearly the whole of its orbit lies below the plane of the ecliptic, and far from the paths of the larger planets, but it extends into space more than twice the distance of Neptune, or nearly six thousand millions of miles from the sun.
Comets in or near their perihelion move with prodigious velocity. That of 1680 appears to have gone half round the sun in ten hours and a half, moving at the rate of 880,000 miles an hour. If its enormous centrifugal force had ceased when passing its perihelion, it would have fallen to the sun in about three minutes, as it was then less than 147,000 miles from his surface. So near the sun, it would be exposed to a heat 27,500 times greater than that received by the earth; and as the sun’s heat is supposed to be in proportion to the intensity of his light, it is probable that a degree of heat so intense would be sufficient to convert into vapour every terrestrial substance with which we are acquainted. At the perihelion distance the sun’s diameter would be seen from the comet under an angle of 73°, so that the sun, viewed from the comet, would nearly cover the whole extent of the heavens from the horizon to the zenith. As this comet is presumed to have a period of 575 years, the major axis of its orbit must be so great, that at the aphelion the sun’s diameter would only subtend an angle of about fourteen seconds, which is not so great by half as the diameter of Mars appears to us when in opposition. The sun would consequently impart no heat, so that the comet 372would then be exposed to the temperature of the ethereal regions, which is 239° below the zero point of Fahrenheit. A body of such tenuity as the comet, moving with such velocity, must have met with great resistance from the dense atmosphere of the sun, while passing so near his surface at its perihelion. The centrifugal force must consequently have been diminished, and the sun’s attraction proportionally augmented, so that it must have come nearer to the sun in 1680 than in its preceding revolution, and would subsequently describe a smaller orbit. As this diminution of its orbit will be repeated at each revolution, the comet will infallibly end by falling on the surface of the sun, unless its course be changed by the disturbing influence of some large body in the unknown expanse of creation. Our ignorance of the actual density of the sun’s atmosphere, of the density of the comet, and of the period of its revolution, renders it impossible to form any idea of the number of centuries which must elapse before this event takes place.
The same cause may affect the motions of the planets, and ultimately be the means of destroying the solar system. But, as Sir John Herschel observes, they could hardly all revolve in the same direction round the sun for so many ages without impressing a corresponding motion on the ethereal medium, which may preserve them from the accumulated effects of its resistance. Should this material medium revolve about the sun like a vortex, it will accelerate the revolutions of such comets as have direct motions, and retard those that have retrograde motions.
The comet which appeared unexpectedly in the beginning of the year 1843 was one of the most splendid that ever visited the solar system. It was in the constellation of Antinous in the end of January, at a distance of 115 millions of miles from the earth, and it passed through its perihelion on the 27th of February, when it was lost in the sun’s rays; but it began to be visible about the 3rd of March, at which time it was near the star Iota Cetæ, and its tail extended towards the Hare. Before the passage at the perihelion it had no tail; but at that epoch the tail suddenly darted out, and extended to a distance of 1826 millions of miles in about an hour and a half—a most inexplicable speed of development, which indicates some powerful repulsive force at the moment of the greatest proximity to the sun, at which time the tails are formed. The brightness of the comet and the length 373of its tail continued to increase till the latter stretched far beyond the constellation of the Hare towards a point above Sirius. Stars were distinctly seen through it, and when near perihelion the comet was so bright that it was seen in clear sunshine, in the United States, like a white cloud. The motion was retrograde, and on leaving the solar system it retreated so rapidly at once from the sun and earth that it was soon lost sight of for want of light. On the 1st of April it was between the sun and the earth, and only 40 millions of miles from the latter; and as its tail was at least 60 millions of miles long, and 20 millions of miles broad, we probably passed through it without being aware of it. There is some discrepancy in the different computations of the elements of the orbit, but in the greater number of cases the perihelion distance was found to be less than the semidiameter of the sun, so that the comet must have grazed his surface, if it did not actually impinge obliquely on him.
The perihelion distance of this comet differs little from that of the great comet of 1668, which came so near the sun. The motion of both was retrograde, and a certain resemblance in the two orbits makes it probable that they are the same body performing a revolution in 175 years.
Though already so well acquainted with the motions of comets, we know nothing of their physical constitution. A vast number, especially of telescopic comets, are only like clouds or masses of vapour, often without tails. The head commonly consists of a concentrated mass of light, like a planet, surrounded by a very transparent atmosphere, and the whole, viewed with a telescope, is so diaphanous, that the smallest star may be seen even through the densest part of the nucleus; in general their solid parts, when they have any, are so minute, that they have no sensible diameter, like that of the comet of 1811, which appeared to Sir William Herschel like a luminous point in the middle of the nebulous matter. The nuclei, which seem to be formed of the denser strata of that nebulous matter in successive coatings, are sometimes of great magnitude. Those comets which came to the sun in the years 1799 and 1807 had nuclei whose diameters measured 180 and 275 leagues respectively, and the second comet of 1811 had a nucleus 1350 leagues in diameter.
It must, however, be stated that, as comets are generally at prodigious distances from the earth, the solid parts of the nuclei 374appear like mere points of light, so minute that it is impossible to measure them with any kind of accuracy, so that the best astronomers often differ in the estimation of their size by one-half of the whole diameter. The transit of a comet across the sun would afford the best information with regard to the nature of the nuclei. It was computed that such an event was to take place in the year 1827; unfortunately the sun was hid by clouds from the British astronomers, but it was examined at Viviers and at Marseilles at the time the comet must have been projected on its disc, but no spot or cloud was to be seen, so that it must have had no solid part whatever. The nuclei of many comets which seemed solid and brilliant to the naked eye have been resolved into mere vapour by telescopes of high powers; in Halley’s comet there was no solid part at all.
The nebulosity immediately round the nucleus is so diaphanous, that it gives little light; but at a small distance the nebulous matter becomes suddenly brilliant, so as to look like a bright ring round the body. Sometimes there are two or three of these luminous concentric rings separated by dark intervals, but they are generally incomplete on the part next the tail.
These annular appearances are an optical effect, arising from a succession of envelopes of the nebulous matter with intervals between them, of which the first is sometimes in contact with the nucleus and sometimes not. The thickness of these bright diaphanous coatings in the comets of 1799 and 1807 was about 7000 and 10,000 leagues respectively; and in the first comet of 1811 the luminous ring was 8000 leagues thick, and the distance between its interior surface and the centre of the head was 10,000 leagues. The latter comet was by much the most brilliant that has been seen in modern times; it was first discovered in this country by Mr. James Vietch of Inchbonny, and was observed in all its changes by Sir William Herschel and M. Olbers. To the naked eye, the head had the appearance of an ill-defined round mass of light, which was resolved into several distinct parts when viewed with a telescope. A very brilliant interior circular mass of nebulous matter was surrounded by a black space having a parabolic form, very distinct from the dark blue of the sky. This dark space was of a very appreciable breadth. Exterior to the black interval there was a luminous parabolic contour of considerable thickness, which was prolonged on each side in two 375diverging branches, which formed the bifid tail of the comet. Sir William Herschel found that the brilliant interior circular mass lost the distinctness of its outline as he increased the magnifying power of the telescope, and presented the appearance of a more and more diffuse mass of greenish or blueish green light, whose intensity decreased gradually, not from the centre, but from an eccentric brilliant speck, supposed to be the truly solid part of the comet. The luminous envelope was of a decided yellow, which contrasted strongly with the greenish tint of the interior nebulous mass. Stars were nearly veiled by the luminous envelope, whilst, on the contrary, Sir William Herschel saw three extremely small stars shining clearly in the black space, which was singularly transparent. As the envelopes were formed in succession as the comet approached the sun, Sir William Herschel conceived them to be vapours raised by his heat at the surface of the nucleus, and suspended round it like a vault or dome by the elastic force of an extensive and highly transparent atmosphere. In coming to the sun, the coatings began to form when the comet was as distant as the orbit of Jupiter, and in its return they very soon entirely vanished; but a new one was formed after it had retreated as far as the orbit of Mars, which lasted for a few days. Indeed, comets in general are subject to sudden and violent convulsions in their interior, even when far from the sun, which produce changes that are visible at enormous distances, and baffle all attempts at explanation—probably arising from electricity, or even causes with which we are unacquainted. The envelopes surrounding the nucleus of the comet on the side next to the sun diverge on the opposite side, where they are prolonged into the form of a hollow cone, which is the tail. Two repulsive forces seem to be concerned in producing this effect; one from the comet and another from the sun, the latter being the most powerful. The envelopes are nearer the centre of the comet on the side next to the sun, where these forces are opposed to one another; but on the other side the forces conspire to form the tail, conveying the nebulous particles to enormous distances.
The lateral edges of the tail reflect more light than the central part, because the line of vision passes through a greater depth of nebulous matter, which produces the effect of two streams somewhat like the aurora. Stars shine with undiminished lustre through the central part of the tail, because their rays traverse it 376perpendicularly to its thickness; but, though distinctly seen through its edges, their light is weakened by its oblique transmission. The tail of the great comet of 1811 was of wonderful tenuity; stars which would have been entirely concealed by the slightest fog were seen through 64,000 leagues of nebulous matter without the smallest refraction. Possibly some part of the changes in the appearance of the tails arises from rotation. Several comets have been observed to rotate about an axis passing through the centre of the tail. That of 1825 performed its rotation in 201⁄2 hours, and the rapid changes in the luminous sectors which issued from the nucleus of Halley’s comet in all probability were owing to rotatory motion.
The two streams of light which form the edges of the tail in most cases unite at a greater or less distance from the nucleus, and are generally situate in the plane of the orbit. The tails follow comets in their descent towards the sun, but precede them in their return, with a small degree of curvature; their apparent extent and form vary according to the positions of the orbits with regard to the ecliptic. In some cases the tail has been at right angles to the line joining the sun and comet. The curvature is in part owing to the resistance of the ether, and partly to the velocity of the comet being greater than that of the particles at the extremity of its tail, which lag behind. The tails are generally of enormous lengths; the comet of 1811 had one no less than a hundred millions of miles in length, and those which appeared in the years 1618, 1680, and 1769, had tails which extended respectively over 104, 90, and 97 degrees of space. Consequently, when the heads of these comets were set, a portion of the extremity of their tails was still in the zenith. Sometimes the tail is divided into several branches, like the comet of 1744, which had six, separated by dark intervals, each of them about 4° broad, and from 30° to 44° long. They were probably formed by three hollow cones of the nebulous matter proceeding from the different envelopes, and enclosing one another, with intervals between; the lateral edges of these cones would give the appearance of six streams of light. The tails do not attain their full magnitude till the comet has left the sun. When comets first appear, they resemble round films of vapour, with little or no tail. As they approach the sun, they increase in brilliancy, and their tail in length, till they are lost in his rays; and it is not 377till they emerge from the sun’s more vivid light that they assume their full splendour. They then gradually decrease, their tails diminish, and they disappear, nearly or altogether, before they are beyond the sphere of telescopic vision. Many comets have no tails, as, for example, Encke’s comet. Those which appeared in the years 1585, 1763, and 1682, were also without tails, though the latter is recorded to have been as bright as Jupiter. The matter of the tail must be extremely buoyant to precede a body moving with such velocity: indeed, the rapidity of its ascent cannot be accounted for. It has been attributed to that power in the sun which produces those vibrations of ether which constitute light; but as this theory will not account for the comet of 1824, which is said to have had two tails, one directed towards the sun, and a very short one diametrically opposite to it, our ignorance on this subject must be confessed. In this case the repelling power of the comet seems to have been greater than that of the sun. Whatever that unknown power may be, there are instances in which its effects are enormous; for, immediately after the great comet of 1680 had passed its perihelion, its tail was 100,000,000 miles in length, and was projected from the comet’s head in the short space of two days. A body of such extreme tenuity as a comet is most likely incapable of an attraction powerful enough to recall matter sent to such an enormous distance; it is therefore, in all probability, scattered in space or absorbed by the zodiacal light or nebula that surrounds the sun, which may account for the rapid decrease observed in the tails of comets every time they return to their perihelia. Should the great comet of 1843 prove to be the same with that of 1668, its tail must have diminished considerably.
It is remarkable that, although the tails of comets increase in length as they approach their perihelia, there is reason to believe that the real diameter of the head contracts on coming near the sun, and expands rapidly on leaving him. Hevelius first observed this phenomenon, which Encke’s comet has exhibited in a very extraordinary degree. On the 28th of October, 1828, this comet was about three times as far from the sun as it was on the 24th of December; yet at the first date its apparent diameter was twenty-five times greater than at the second, the decrease being progressive. M. Valz attributes the circumstance to a real condensation of volume from the pressure of the ethereal medium, 378which increases most rapidly in density towards the surface of the sun, and forms an extensive atmosphere around him. It did not occur to M. Valz, however, that the ethereal fluid would penetrate the nebulous matter instead of compressing it. Sir John Herschel, on the contrary, conjectures that it may be owing to the alternate conversion of evaporable materials in the upper regions of the transparent atmosphere of comets into the states of visible cloud and invisible gas by the effects of heat and cold; or that some of the external nebulous envelopes may come into view when the comet arrives at a darker part of the sky, which were overpowered by the superior light of the sun while in his vicinity. The first of these hypotheses he considers to be perfectly confirmed by his observations on Halley’s comet, made at the Cape of Good Hope, after its return from the sun. He thinks that, in all probability, the whole comet, except the densest part of its head, vanished, and was reduced to a transparent and invisible state during its passage at its perihelion: for when it first came into view, after leaving the sun, it had no tail, and its aspect was completely changed. A parabolic envelope soon began to appear, and increased so much and so rapidly that its augmentation was visible to the eye. This increase continued till it became so large and so faint, that at last it vanished entirely, leaving only the nucleus and a tail, which it had again acquired, but which also vanished; so that at last the nucleus alone remained. Not only the tails, but the nebulous part of comets, diminishes every time they return to their perihelia; after frequent returns they ought to lose it altogether, and present the appearance of a fixed nucleus: this ought to happen sooner to comets of short periods. M. de la Place supposes that the comet of 1682 must be approaching rapidly to that state. Should the substances be altogether, or even to a great degree, evaporated, the comet would disappear for ever. Possibly comets may have vanished from our view sooner than they would otherwise have done from this cause.
The comet discovered at Florence by Signore Donati, on the 2nd of June, 1858, was one of the most beautiful that has been seen from our planet for many years, whether for the brightness of the nucleus, or the length and graceful form of the coma; when first discovered it was near the star λ in the constellation of the Lion, being then at a distance of 288,000,000 379miles from the earth; during the month of August its nucleus assumed an almost planetary aspect from the concentration of its light; on the 27th of September the head appeared almost as bright as Mercury, but smaller; when near its perihelion passage, on September 30th, its diameter, as ascertained by Signore Donati, was 3ʺ; during the early part of October it continued to increase in brilliancy, the tail becoming more elongated, and describing a beautiful arc in the heavens, occupying a space of nearly 40°, or a length of 40,000,000 miles in the solar system. On the evening of the 5th of October it was seen from most parts of Britain, within 20ʹ of Arcturus, the brightest star in the northern heavens, across which the densest part nearly of the tail passed, and through which notwithstanding the star shone with undiminished brilliancy. On the 30th of October, when in perihelio, the comet was only 55,000,000 miles from the sun; on the 10th it approached nearest to the earth, from which it was then distant 51,000,000 miles; and on the 15th of the same month near to Venus, being at that time less than one-tenth the distance of the earth from the Sun; if the comet had reached its perihelion a few days earlier, Venus might have passed through its nucleus, the consequences of which to the planet it would be very difficult to imagine. The motion of Donati’s comet is what astronomer’s call retrograde, or from east to west. It ceased to be visible in our northern latitudes in the last week in October, having passed into the southern heavens, where it will traverse the constellations of Sagittarius, Telescopium, and Indus, approaching the large star of Toucan; after which it will disappear until it has nearly completed its revolution round the sun. The observed orbit of this remarkable comet coincides more nearly with an ellipse than a parabola; the longer diameter of the ellipse being 184 times that of the earth’s orbit, or the immense distance of 35,100,000,000 miles—a space which, however great, is less than the thousandth of the distance of the nearest fixed star. According to the calculations of M. Loewy, and adopting an elliptic orbit, Donati’s comet will not return to the same places in the heavens for 2495 years, being 500 less than the period of revolution of the great comet of 1811.
Signore Donati observed that between the 25th and 30th September two concentric, luminous, semicircular envelopes, with a 380dark space between them, were formed in the head. From the extremities of these the cone of the tail extended, and a non-luminous or dark space stretched for 20° from the nucleus into the tail. On the 1st October the two envelopes were combined into one. This comet, like Halley’s, has shown some singular irregularities, supposed to arise from the action of the sun when near its perihelion. At different periods of its apparition a violent agitation was observed in its nucleus, with luminous jets, spiral offshoots, &c., as in the great comets of 1680, 1744, 1811. A ray of light was thrown out from one side of the nucleus towards the sun, while a gas-like jet proceeded from the other side, which appeared to form the origin of a second tail within the great tail, and which was traced for half a degree by Mr. Hind on the 19th September. He observed decided spiral convolutions in the tail, which show that this comet has a rotatory motion about an axis passing through the tail.
If comets shine by borrowed light, they ought, in certain positions, to exhibit phases like the moon; but no such appearance has been detected, except in one instance, when they are said to have been observed by Hevelius and La Hire, in the year 1682. In general, the light of comets is dull—that of the comet of 1811 was only equal to the tenth part of the light of the full moon—yet some have been brilliant enough to be visible in full daylight, especially the comet of 1744, which was seen without a telescope at one o’clock in the afternoon, while the sun was shining. Hence it may be inferred that, although some comets may be altogether diaphanous, others seem to possess a solid mass resembling a planet. But whether they shine by their own or by reflected light has never been satisfactorily made out till now. Even if the light of a comet were polarized, it would not afford a decisive test, since a body is capable of reflecting light, though it shines by its own. M. Arago, however, has, with great ingenuity, discovered a method of ascertaining this point, independent both of phases and polarization.
Since the rays of light diverge from a luminous point, they will be scattered over a greater space as the distance increases, so that the intensity of the light on a screen two feet from the object is four times less than at the distance of one foot; three feet from the object it is nine times less; and so on, decreasing in intensity as the square of the distance increases. As a self-luminous 381surface consists of an infinite number of luminous points, it is clear that, the greater the extent of surface, the more intense will be the light; whence it may be concluded that the illuminating power of such a surface is proportional to its extent, and decreases inversely as the square of the distance. Notwithstanding this, a self-luminous surface, plane or curved, viewed through a hole in a plate of metal, is of the same brilliancy at all possible distances as long as it subtends a sensible angle, because, as the distance increases, a greater portion comes into view; and, as the augmentation of surface is as the square of the diameter of the part seen through the whole, it increases as the square of the distance. Hence, though the number of rays from any one point of the surface which pass through the hole decreases inversely as the square of the distance, yet, as the extent of surface which comes into view increases also in that ratio, the brightness of the object is the same to the eye as long as it has a sensible diameter. For example—Uranus is about nineteen times farther from the sun than we are, so that the sun, seen from that planet, must appear like a star with a diameter of a hundred seconds, and must have the same brilliancy to the inhabitants that he would have to us if viewed through a small circular hole having a diameter of a hundred seconds. For it is obvious that light comes from every point of the sun’s surface to Uranus, whereas a very small portion of his disc is visible through the hole; so that extent of surface exactly compensates distance. Since, then, the visibility of a self-luminous object does not depend upon the angle it subtends as long as it is of sensible magnitude, if a comet shines by its own light, it should retain its brilliancy as long as its diameter is of a sensible magnitude; and, even after it has lost an apparent diameter, it ought to be visible, like the fixed stars, and should only vanish in consequence of extreme remoteness. That, however, is far from being the case—comets gradually become dim as their distance increases, and vanish merely from loss of light, while they still retain a sensible diameter, which is proved by observations made the evening before they disappear. It may therefore be concluded that comets shine by reflecting the sun’s light. The most brilliant comets have hitherto ceased to be visible when about five times as far from the sun as we are. Most of the comets that have been visible from the earth have their perihelia within the orbit of Mars, 382because they are invisible when as distant as the orbit of Saturn: on that account there is not one on record whose perihelion is situate beyond the orbit of Jupiter. Indeed, the comet of 1756, after its last appearance, remained five whole years within the ellipse described by Saturn without being once seen. More than a hundred and forty comets have appeared within the earth’s orbit during the last century that have not again been seen. If a thousand years be allowed as the average period of each, it may be computed, by the theory of probabilities, that the whole number which range within the earth’s orbit must be 1400; but, Uranus being about nineteen times more distant, there may be no less than 11,200,000 comets that come within the orbit of Uranus. M. Arago makes a different estimate; he considers that, as thirty comets are known to have their perihelion distance within the orbit of Mercury, if it be assumed that comets are uniformly distributed in space, the number having their perihelion within the orbit of Uranus must be to thirty as the cube of the radius of the orbit of Uranus to the cube of the radius of the orbit of Mercury, which makes the number of comets amount to 3,529,470. But that number may be doubled, if it be considered that, in consequence of daylight, fogs, and great southern declination, one comet out of two must be hid from us. According to M. Arago, more than seven millions of comets come within the orbit of Uranus.
The different degrees of velocity with which the planets and comets were originally propelled in space is the sole cause of the diversity in the form of their orbits, which depends only upon the mutual relation between the projectile force and the sun’s attraction.
When the two forces are exactly equal to one another, circular motion is produced; when the ratio of the projectile to the central force is exactly that of 1 to the square root of 2, the motion is parabolic; any ratio between these two will cause a body to move in an ellipse, and any ratio greater than that of 1 to the square root of 2 will produce hyperbolic motion (N. 229).
The celestial bodies might move in any one of these four curves by the law of gravitation: but, as one particular velocity is necessary to produce either circular or parabolic motion, such motions can hardly be supposed to exist in the solar system, where the bodies are liable to such mutual disturbances as would 383infallibly change the ratio of the forces, and cause them to move in ellipses in the first case, and hyperbolas in the other. On the contrary, since every ratio between equality and that of 1 to the square root of 2 will produce elliptical motion, it is found in the solar system in all its varieties, from that which is nearly circular to such as borders on the parabolic from excessive ellipticity. On this depends the stability of the system; the mutual disturbances only cause the orbits to become more or less excentric without changing their nature.
For the same reason the bodies of the solar system might have moved in an infinite variety of hyperbolas, since any ratio of the forces, greater than that which causes parabolic motion, will make a body move in one of these curves. Hyperbolic motion is however very rare; only two comets appear to move in orbits of that nature, those of 1771 and 1824; probably all such comets have already come to their perihelia, and consequently will never return.
The ratio of the forces which fixed the nature of the celestial orbits is thus easily explained; but the circumstances which determined these ratios, which caused some bodies to move nearly in circles and others to wander towards the limits of the solar attraction, and which made all the heavenly bodies to rotate and revolve in the same direction, must have had their origin in the primeval state of things; but as it pleases the Supreme Intelligence to employ gravitation alone in the maintenance of this fair system, it may be presumed to have presided at its creation.
The Fixed Stars—Their Number—The Milky Way—Double Stars—Binary Systems—Their Orbits and Periodic Times—Colours of the Stars—Stars that have vanished—Variable Stars—Variation in Sun’s Light—Parallax and Distances of the Fixed Stars—Masses of the Stars—Comparative Light of the Stars—Proper Motions of the Stars—Apparent Motions of the Stars—Motion and Velocity of the Sun and Solar System—The Nebulæ—Their Number—Catalogue of them—Consist of Two Classes—Diffuse Nebulæ—Definitely formed Nebulæ—Globular Clusters—Splendour of Milky Way—Distribution of the Nebulæ—The Magellanic Clouds—Nebulæ round η Argûs—Constitution of Nebulæ, and the Forces that maintain them—Meteorites and Shooting Stars.
Great as the number of comets appears to be, it is absolutely nothing in comparison of the multitude of the fixed stars. About 2000 only are visible to the naked eye; but when the heavens are viewed through a telescope, their number seems to be limited only by the imperfection of the instrument. The number registered amounts to 200,000; their places are determined with great precision, and they are formed into a catalogue, not only for the purpose of ascertaining geographical positions by the occultations of the brightest among them, but also to serve as points of reference for marking the places of comets and other celestial phenomena. Sirius, α Centauri, and Arcturus are the brightest stars in the heavens; the others are classed according to their apparent lustre, from the first to the seventeenth magnitudes. Capella, α Lyræ, Procyon, and twenty or twenty-one more, are of the first magnitude; α Persei, γ Orionis, α Cygni, and in all fifty or sixty, are of the second; and of the third there are about 200, such as η Bootis and η Draconis, the numbers increasing as the magnitude diminishes. Those of the eighth magnitude are scarcely visible to the naked eye, and it requires a very good telescope to see stars of the seventeenth. This sequence is perfectly arbitrary; but Sir John Herschel has ascertained by actual measurement the comparative lustre of a great many—for example, he found that the light of a star of the sixth 385magnitude is 100 times less than that of one of the first magnitude, and that Sirius would make between three and four hundred of such little stars. Were the photometric scale completed, it would be of the greatest importance with regard to the variable stars.
The three or four brightest classes of stars are scattered pretty equably over the sky, with the exception of a zone or belt following the course of the great circle passing through ε Orionis and α Crucis, where they are very numerous, especially in the southern hemisphere. The stars of all magnitudes visible to the naked eye increase in numbers towards the borders of the Milky Way, which derives its lustre and name from the diffused light of myriads of stars; so numerous are they in some parts of it that more than 50,000 passed through the field of Sir William Herschel’s telescope in the course of an hour, in a zone only two degrees broad; in many places they are numerous beyond estimation, and most of them are extremely small on account of their enormous distances.
The Milky Way, which forms so conspicuous a part of the firmament, is a vast and somewhat flattened stratum or congeries of stars, encircling the heavens in a broad band, split through one part of its circumference into two streams of stars, bearing a strong resemblance to fig. 5, plate 5. It is contorted and broken in some places, and occasionally lengthened into branches stretching far into space. Its thickness is small compared with its length and breadth; yet in some places it is unfathomable even with the best telescopes; in others there is reason to believe that it is possible to see through it, and even beyond it, in its own plane. There is a gradual but rapid increase in the crowding of the stars on each side of the flat stratum towards the centre.
The solar system is deeply though excentrically plunged into this mass of stars, near that point where the circular stratum splits into two streams. Sir John Herschel’s description of the stars of the southern hemisphere shows that the Milky Way is a most magnificent object there. “The general aspect of the southern circumpolar regions (including in that expression 60° or 70° of south polar distance) is in a high degree rich and magnificent, owing to the superior brilliancy and large development of the Milky Way, which, from the constellation of Orion to 386that of Antinous, is a blaze of light, strangely interrupted, however, with vacant and entirely starless patches, especially in Scorpio, near α Centauri and the Cross, while to the north it fades away pale and dim, and is in comparison hardly traceable. I think it is impossible to view this splendid zone, with the astonishingly rich and evenly distributed fringe of stars of the 3rd and 4th magnitude, which forms a broad skirt to its southern border like a vast curtain, without an impression amounting almost to conviction, that the Milky Way is not a mere stratum, but annular, or at least that our system is placed within one of the poorer or almost vacant parts of its general mass, and that eccentrically, so as to be much nearer to the region about the Cross than to that diametrically opposite to it.”
Those dark vacuities called “Coal Sacks” by the ancient navigators, which are so numerous between α Centauri and α Antaris, are among the most extraordinary phenomena in the southern hemisphere; they are of intense blackness, though by no means void of extremely small telescopic stars; the darkness arises from the contrast these nearly vacant spaces form with the excessive brilliancy of the surrounding part of the Milky Way, and the sudden sharp transition from light to darkness. The largest and most conspicuous of them is a pear-shaped vacuity close to the Southern Cross. That portion of the Milky Way that is split longitudinally through its centre lies between α Centauri and the constellation of Cygnus: the two bands are joined here and there by narrow bridges of condensed stars, stretching across the darker space between them. In Scorpio and Sagittarius Sir John Herschel describes the Milky Way as composed of definite clouds of light running into clusters of extremely minute stars like sand, not strewed evenly as with a sieve, but as if thrown down by handfuls, and by both hands at once, leaving dark intervals. In this astonishing profusion the stars are of all sizes, from the 14th to the 20th magnitude, and even down to nebulosity. After an interval the same profusion is renewed, the stars being inconceivably minute and numerous beyond description—they are in millions and millions. Thus there is great irregularity in their diffusion as well as magnitude—in some places intensely crowded, in others the deep blackness of the sky, over which they are thinly scattered, irresistibly led to believe that in these regions the power of our telescopes fairly 387penetrates through the starry stratum, and beyond it. Sometimes we look through a sheet of stars nearly of the same size, of no great thickness compared with their distance from us, and not unfrequently there is a double stratum, one of large stars spread over another of very small ones.
The most southerly of the two streams of stars which form the Milky Way in this part of the firmament maintains an unbroken course of extreme brilliancy, containing some of the finest clusters of stars in the heavens. One round γ Sagittarii is an intense aggregate of stars, in some parts of which they are so crowded as to exceed enumeration; at a very moderate estimate Sir John Herschel thinks this group cannot contain fewer than a hundred thousand stars. Other two groups between the constellations of the Shield and Ophiuchus stand out like promontories of intense brilliancy in the dark space that separates the starry streams of the Milky Way.
The distance of the fixed stars is too great to admit of their exhibiting a sensible disc, but they must be spherical if gravitation pervades all space, as there is every reason to believe it does. With a powerful telescope the stars are like points of light: their occultations by the moon are therefore instantaneous. Their twinkling arises from sudden changes in the refractive power of the air, which would not be sensible if they had discs like planets. Thus nothing can be known of their distance from us or from one another by their apparent diameters. Although from the appearance of the stars no inference can be drawn as to their distance, yet among the multitudes in the heavens a few are found near enough to exhibit distinct parallactic motions arising from the revolution of the earth in its orbit, from whence their distance from the sun has been computed: α Centauri, the brightest star in the southern hemisphere, is a very remarkable instance. Professor Henderson at the Cape of Good Hope determined its parallax to be 1ʺ by a series of observations on its position at opposite periods of the year, that is, from opposite points in the earth’s orbit. The result was afterwards confirmed by Mr. Maclear, who found the amount to be 0ʺ·913. The difference between the two is wonderfully small, considering the many unavoidable sources of error in the determination of such minute quantities (N. 230).
Since no star in the northern hemisphere has so great an amount 388of parallax, an arc of 1ʺ is assumed as the parallactic unit. Now radius is to the sine of 1ʺ as 206,265 is to 1; hence, α Centauri is 206,265 times more distant from the sun than the sun is from the earth. Light flying at the rate of 192,000 miles in a second must take 3 years and 83 days to come to us from that star.
One or two tenths of a second becomes a very great error when the maximum amount of parallax is only 1ʺ, and on that account, with the exception of α Centauri, it has been found impracticable to determine the annual changes in the apparent motions of single stars affected by precession, nutation, aberration, and the variations of temperature of the instruments used in observing. However, as two stars in juxtaposition are equally affected by all of these; the difference in their motions is independent of them. Of two stars apparently in close approximation, one may be far behind the other in space. They may seem near to one another when viewed from the earth in one part of its orbit, but may separate widely when seen from the earth in another position, just as two terrestrial objects appear to be one when viewed in the same straight line, but separate as the observer changes his position. In this case the stars would not have real, but only apparent motion. One of them would seem to oscillate annually to and fro in a straight line on each side of the other, a motion that could not be mistaken for that of a binary system where one star describes an ellipse about the other; or if the edge of the orbit be turned towards the earth, where the oscillations require years for their accomplishment. The only circumstances that can affect the stars unequally, and which must be eliminated, are the proper motion of the stars in space, and specific aberration, a very minute quantity arising from peculiarities in the star’s light. This method of finding the distances of the fixed stars was proposed by Galileo and attempted by Dr. Long without success. Sir William Herschel afterwards applied it to some of the binary groups; and although he did not find the thing he sought for, it led to the discovery of the orbital motions of the double stars.
M. Struve was the first to apply this method, and that in a very difficult case. He perceived that a very small star is close to α Lyræ, and by a series of most accurate differential measurements from 1835 to 1838 he found that α Lyræ has a parallax of 0ʺ·261, which was afterwards corroborated by the observations of 389M. Peters; hence α Lyræ is 789,600 times more distant from the sun than the earth is.
It was natural to suppose that in general the large stars are nearer to the earth than the small ones; but there is now reason to believe that some stars, though by no means brilliant, are nearer to us than others which shine with greater splendour. This is inferred from the comparative velocity of their proper motions; all the stars have a general motion of translation, which tends ultimately to mix those of the different constellations; but none that we know of moves so rapidly as 61 Cygni, and on that account it was reckoned to be nearer to us than any other, for an object seems to move more quickly the nearer it is. Now M. Bessel saw that two minute and probably very remote stars are very near 61 Cygni, their directions from that star being at right angles to one another; so that, during the revolution of the earth, one of these distances was a maximum and the other a minimum alternately every three months. This alternation, although it indicated a parallax or difference of parallaxes of only 0ʺ·348, was maintained with such perfect regularity every three months, that it leaves not a doubt of its accuracy, which was afterwards confirmed by the observations of M. Peters at Polkova. It follows from that small parallax that 61 Cygni must be 592,700 times farther from the earth than the sun is—a distance that light would not pass over in less than nine years and three months.
Mr. Henderson found the parallax of Sirius, the brightest of all the stars, to be only 0ʺ·230; it is consequently more distant than 61 Cygni, though the latter is but of the 6th magnitude.
M. Argelander has calculated that the apparent magnitude of the stars depends upon their distance. Supposing them all to be of the same size, the smallest visible in Sir William Herschel’s 20 feet reflecting telescope, namely those of the 17th magnitude, would be 228 times farther off than those of the first magnitude; and M. Peters of Polkova from the annual parallax of thirty-five, seven of which are now very accurately determined, has ascertained the distance of the nearest of them to be such, that light flying at the rate of 95 millions of miles in a second would take 15 years and a half to come from them to the earth, and that a star of the 17th magnitude might be extinguished for 3541 years before we should be aware of it. (N. 231.)
390The great gulfs that separate the stars from the sun, and probably from one another, no doubt maintain the stability of the stellar system, in the same manner that in the solar system the distances of the planets from the sun and the satellites from their primaries are so arranged as to preserve their mutual disturbances within due limits. The stars supposed to be nearest the sun are probably in a great zone which crosses the Milky Way between η Argûs and α Crucis. It comprises the bright stars of the constellations Orion, Canis Major, the Southern Cross, Centaur, Lupus, and Scorpio. The axis of the zone is inclined at an angle of 20° to the medial line, or circle, passing through the centre of the Milky Way.
A very great number of stars undergo periodical changes of lustre, varying in some cases from complete extinction to their original brilliancy, strongly suggesting the idea that they are temporarily obscured, and sometimes completely hid, by opaque bodies revolving round them in regular periodic times, as the planets do about the sun.
The star Mira, or ω Ceti, which was first noticed to be periodical by Fabricius, in 1596, appears about twelve times in eleven years, or in periods of 331d 8h 4m 16s; it remains at its greatest brightness about a fortnight, being then on some occasions equal to a large star of the second magnitude; then it decreases during about three months, till it becomes completely invisible to the naked eye, in which state it remains about five months; after that it continues increasing during the remainder of its period. Such is the general course of its changes; but it does not always return to the same degree of brightness, nor increase and diminish by the same gradations, neither are the successive intervals of its maxima equal. From the observations and investigations of M. Argelander, the mean period given is subject to fluctuation, embracing 88 such periods, and having the effect of gradually lengthening and shortening alternately those intervals to the extent of 25 days one way and the other. The irregularities in the degree of brightness attained at the maximum are probably also periodical. For four years previous to 1676 it did not appear at all; and on October 5, 1839, it exceeded α Ceti, and equalled β Aurigæ, in lustre. These irregularities may be occasioned by periodical perturbations among opaque bodies revolving about the star. Algol, or β Persei, is another very remarkable 391instance of a variable star. It has the size of a star of the second magnitude for two days and thirteen and a half hours, and then suddenly begins to diminish in splendour, till, in about three hours and a half, it is reduced to the size of a star of the fourth magnitude; it then begins again to increase, and in three hours and a half more regains its brightness, going through all these vicissitudes in 2d 20h 48m 54s·7. Sir John Herschel and Mr. Goodricke, by whom the variable nature of this star was discovered in 1782, considered this to be a case strongly indicative of the revolution of an opaque body, which, coming between us and Algol, cuts off a large portion of the light. This star has been constantly observed, and the more recent observations, compared with the ancient ones, indicated a diminution in the periodic time. It is even proved that this decrease is not uniformly progressive, but is actually proceeding with accelerated rapidity, which, however, will probably not continue, but will by degrees relax, and then be changed into increase, according to the laws of periodicity, which, as well as their causes, remain to be discovered. The first minimum of this star, in 1844, happened on January 3rd, at 4h 14m Greenwich time. γ Hydræ also vanishes and reappears every 494 days. β Lyræ was discovered to be variable, in 1784, by Mr. Goodricke, and its period was ascertained by Argelander to be 12d 21h 53m 10s, in which time a double maximum and minimum takes place, the two maxima being nearly equal, but the two minima unequal; besides these semi-periods, there is a slow aberration of period, which appears to be periodical itself: from its discovery to 1840 the time was continually lengthening, but more and more slowly, till, in 1840, it ceased to increase, and has since been slowly on the decrease.
The stars δ Cephei and η Aquilæ, or Antinoi, were discovered to be variable in 1784; their respective periods, being 5d 8h 47m 39s and 7d 4h 13m 53s, have since been accurately determined. Besides these, the variations of between 30 and 40 have been approximately ascertained, and a great many more among the smaller stars have been discovered to be variable by Mr. Hind, who has remarked that many of those stars which continue visible at their minimum appear hazy and indistinct, as though some cloudy or nebulous medium intervened. Some of the variable stars are red, and others present successive changes through blue, yellow, and red. When the brightness is increasing the star has a blueish tinge, 392when it is past its maximum lustre it assumes a yellow tint, and while on its decrease it becomes ruddy with flashes of bright red light. These changes are very marked in a small star near the star 77, at the extremity of the south wing of Virgo.
Sir John Herschel, after having described the glory of the starry heavens, asks, “For what purpose are we to suppose such magnificent bodies scattered through the abyss of space? Surely not to illuminate our nights, which an additional moon of the thousandth part the size of our own would do much better, nor to sparkle as a pageant void of meaning and reality, and bewilder us with vain conjectures. Useful, it is true, they are to man as points of exact and permanent reference; but he must have studied astronomy to little purpose who can suppose man to be the only object of his Creator’s care, or who does not see in the vast and wonderful apparatus around us provision for other races of animated beings. The planets, we have seen, derive their light from the sun, but that cannot be the case with the stars. These doubtless then are themselves suns, and may perhaps, each in its sphere, be the presiding centre round which other planets or bodies, of which we can form no conception from any analogy offered by our own system, may be circulating.”
Another circumstance shows how probable it is that dark bodies are revolving among the stars. The proper motion of Sirius is very irregular—sometimes it is rapid, and at other times slow; the cause is ascribed by MM. Bessel and Peters to a dark companion which revolves with Sirius about their common centre of gravity, and by its attraction disturbs the equable motion of the star.
Sometimes stars have all at once appeared, shone with a bright light, and vanished. Several instances of these temporary stars are on record. A remarkable one occurred in the year 125, which is said to have induced Hipparchus to form the first catalogue of stars. Another star appeared suddenly near α Aquilæ in the year 389, which vanished after remaining for three weeks as bright as Venus. On the 10th of October, 1604, a brilliant star burst forth in the constellation of Serpentarius, which continued visible for a year; and on the 11th of November, 1572, a star all at once shone forth in Cassiopeia, which rapidly increased in brightness till it surpassed that of Jupiter so much as to be visible at midday. It began to decrease in December of 393the same year, and, in March, 1574, it had entirely disappeared, having exhibited a variety of tints. It is suspected, however, that this star is periodically variable and identical with stars which appeared in the years 945 and 1264. A more recent case occurred in the year 1670, when a new star was discovered in the head of the Swan, which, after becoming invisible, reappeared, and, having undergone many variations in light, vanished after two years, and has never since been seen. On the 28th of April, 1848, Mr. Hind discovered a star of the 5th magnitude in the constellation Ophiuchus, which was very conspicuous to the naked eye, and where he was certain no star even so bright as the 9th magnitude had ever existed, nor was there any record of such a star. From the time of its discovery it continued to diminish till it became extinct. Its colour was ruddy, and was thought to undergo remarkable changes, probably an effect of its low position, as its polar distance was 102° 39ʹ 14ʺ.
Sir John Herschel discovered very singular variations in the star η of the constellation Argo. It is surrounded by a wonderful nebula, and between the years 1677 and 1826 it varied twice from the 4th to the 2nd magnitude; but in the beginning of 1838 it suddenly increased in lustre, so as to be nearly as bright as α Centauri. Thence it diminished, but not below the first magnitude till April 1843, when it had again increased, so as to surpass Canopus, and nearly equal Sirius in splendour. With regard to this singular phenomenon, Sir John Herschel observes, that “Temporary stars heretofore recorded have all become totally extinct. Variable stars, as far as they have been carefully attended to, have exhibited periodical and regular alternations (in some degree at least) of splendour and comparative obscurity; but here we have a star fitfully variable to an astonishing extent, and whose fluctuations are spread over centuries, apparently in no settled period, and in no regular progression. What origin can we ascribe to these sudden flashes and relapses? What conclusions are we to draw as to the comfort or habitability of a system depending for its supply of light and heat on so variable a source? Its future career will be a subject of high physical interest. To this account I will only add, that in the beginning of 1838 the brightness of this star was so great as materially to interfere with the observations of that part of the nebula surrounding it.” Sir John has also discovered that α Orionis is variable, a circumstance 394the more remarkable as it is one of the conspicuous stars of our hemisphere, and yet its changes had never been remarked. The inferences Sir John draws from the phenomena of variable stars are too interesting not to be given in his own words. “A periodic change existing to so great an extent in so large and brilliant a star as α Orionis cannot fail to awaken attention to the subject, and to revive the consideration of those speculations respecting the possibility of a change in the lustre of our sun itself, which were first put forth by my father. If there be really a community of nature between the sun and the fixed stars, every proof that we obtain of the extensive prevalence of such periodical changes in those remote bodies adds to the probability of finding something of the kind nearer home. If our sun were ever intrinsically much brighter than at present, the mean temperature of the surface of our globe would of course be proportionally greater. I speak now not of periodical, but secular changes. But the argument is complicated with the consideration of the possible imperfect transparency of space, which may be due to material non-luminous particles, diffused irregularly in patches analogous to nebulæ, but of great extent—to cosmical clouds, in short, of whose existence we have, I think, some indication in the singular and apparently capricious phenomena of temporary stars, and perhaps in the recent extraordinary increase, and hardly less sudden diminution, of η Argûs.” Mr. Hind has come to the same conclusion with Goodricke and Sir John Herschel, that the changes in the variable stars are owing to opaque bodies revolving round them; indeed there are strong reasons to believe that there are solar systems analogous to our own in the remote regions of space. Our sun requires nine times the period of Algol to perform a revolution on its axis, while, on the other hand, the periodic time of an opaque revolving body, sufficiently large to produce a similar temporary obscuration of the sun seen from a fixed star, would be less than fourteen hours.
It is possible that the decrease of light in some of the variable stars may arise from large spots on their surface, like those occasionally seen in the radiant fluid masses on the surface of the sun. One of these spots which was measured by Sir John Herschel on the 20th of March, 1836, with its penumbra, occupied an area of 3780 millions of square miles; and the black central part of 395a spot that appeared on the 25th of May following would have allowed the globe of the earth to drop through it, leaving a thousand miles clear of contact all around this tremendous abyss.
All the variable stars on record of which the places are distinctly indicated have occurred without exception in, or close upon, the borders of the Milky Way, and that only within the following semicircle, the preceding having offered no example of the kind.
Many stars have actually disappeared from the heavens. 42 Virginis seems to be of the number, having been missed by Sir John Herschel on the 9th of May, 1828, and not again found, though he frequently had occasion to observe that part of the sky. Mr. Cooper, of the Markree Observatory, has given a list of fifty stars that are missing since the publication of his list of stars in 1847. Comparing the present state of the heavens with more ancient catalogues, a much greater number have disappeared.
Thousands of stars that seem to be only brilliant points of light, when carefully examined are found to be in reality systems of two or more suns, many of which are known to revolve about one another. These binary and multiple systems are very remote, requiring powerful telescopes to show the stars separately. They are divided into eight classes, according to the proximity of the two stars. The first class comprises only such as are less than 1ʺ of space apart; those of the second class are more apart than 1ʺ and less than 2ʺ, &c. &c. Sometimes the two stars are of equal magnitude, but more frequently a conspicuous star is accompanied by a smaller companion. In some cases the conspicuous star itself is double, as in ζ Cancri, ξ Scorpio, 11 Monocerotis, and 12 Lyncis, which are triple stars. Each of the two stars of ε Lyræ is a beautiful and close double star; so that which in a common telescope appears merely to be a double star, is found to be quadruple with a very excellent instrument. The multiple system of θ Orionis is one of the most remarkable objects in our hemisphere. To the naked eye and with an ordinary telescope it seems to be a single star, but it really consists of four brilliant stars forming a trapezium, and accompanied by two excessively minute and very close companions, to perceive both of which is the severest test of a telescope.
The first catalogue of double stars in which their places and relative positions are given was accomplished by the talent and industry of Sir William Herschel, who made so many great discoveries, 396and with whom the idea of their combination in binary and multiple systems originated; and that important fact he established by the discovery of a revolving motion in 50 or 60, and by the determination of the revolution of one star about the other of Castor or α Geminorum, the largest and finest double star in the northern hemisphere. He even assigned the approximate periodic times of this and of several other binary systems. More than 100 stars are now known to be stellar systems. The positions of many hundreds were measured by Sir John Herschel and Sir James South; and the catalogue of the double stars in the northern hemisphere, which have been micrometrically measured, has been increased to more than 6000 by MM. Bessel, Struve, and British astronomers.
Extensive catalogues of double stars in the southern hemisphere have been published by the astronomers in our colonial establishments. To these Sir John Herschel added 1081 during his residence at the Cape of Good Hope: the angles of position and distances of the stars from one another he measured, and found that many of them have very rapid orbital motions. The elliptical elements of the orbits and periodic times of fifteen have been determined by the most eminent astronomers with wonderful accuracy, considering the enormous distances and the extreme delicacy and difficulty of the subject. M. Savary has the merit of having first determined the elements of the orbit of a double star from observation. The difficulty of doing so is great, because the nearest fixed star is 211,000 times farther from the sun than the earth is, and the orbit itself is only visible with the best telescopes; consequently a very small error in observation occasions an enormous error in the determination of quantities at that distance.
In observing the relative position of the stars of a binary system, the distance between them, and also the angle of position, that is, the angle which the meridian, or a parallel to the equator, makes with the line joining the two stars, are measured. The different values of the angle of position show whether the revolving star moves from east to west, or the contrary; whether the motion be uniform or variable, and at what points it is greatest or least. The measures of the distances show whether the two stars approach or recede from one another. From these the form and nature of the orbit are determined. Were observations 397perfectly accurate, four values of the angle of position, and of the corresponding distances at given epochs, would be sufficient to assign the form and position of the curve described by the revolving star; this, however, scarcely ever happens. The accuracy of each result depends upon taking the mean of a great number of the best observations, and eliminating error by mutual comparison. The distances between the stars are so minute that they cannot be measured with the same accuracy as the angles of position; therefore, in order to determine the orbit of a star independently of the distance, it is necessary to assume, as the most probable hypothesis, that the stars are subject to the law of gravitation, and consequently that one of the two stars revolves in an ellipse about the other, supposed to be at rest, though not necessarily in the focus. A curve is thus constructed graphically by means of the angles of position and the corresponding times of observation. The angular velocities of the stars are obtained by drawing tangents to this curve at stated intervals, whence the apparent distances, or radii vectores of the revolving star, become known for each angle of position, because, by the laws of elliptical motion, they are equal to the square roots of the apparent angular velocities. Now that the angles of position estimated from a given line, and the corresponding distances of the two stars, are known, another curve may be drawn, which will represent on paper the actual orbit of the star projected on the visible surface of the heavens; so that the elliptical elements of the true orbit, and its position in space, may be determined by a combined system of measurements and computation. But, as this orbit has been obtained on the hypothesis that gravitation prevails in these distant regions, which could not be known à priori, it must be compared with as many observations as can be obtained, to ascertain how far the computed ellipse agrees with the curve actually described by the star.
γ Virginis consists of two stars of nearly the same magnitude; they were so far apart in the beginning and middle of last century, that they were mentioned by Bradley, and marked in Mayer’s catalogue, as two distinct stars. Since that time they have been continually approaching each other, till in January, 1836, one star was seen to eclipse the other, by Admiral Smyth at his Observatory at Bedford, and by Sir John Herschel at the Cape of Good Hope. A series of observations since the beginning of the 398present century has enabled Sir John to determine the form and position of the elliptical orbit of the revolving star with extraordinary truth by the preceding method. According to his calculation, it came to its perihelion on the 18th of August of the year 1834. Its previous velocity was so great that the revolving star described an angle of 68° in one year. By the laws of elliptical motion its angular velocity must diminish till it arrives at its aphelion. The accuracy with which the motions of the binary systems are measured, and the skill employed in the deduction of the elliptical elements, are now so great, that the periodic time of γ Virginis, determined by Sir John Herschel and Admiral Smyth from their respective observatories, combined with those of Sir William Herschel, only differ by two years, Sir John having obtained a period of 182 years, Admiral Smyth that of 180. By the aid of more numerous observations Mr. Fletcher has found that the true period is 184·53 years, and that the revolving star passed its perihelion in 1837. It is by such successive steps that astronomy is brought to perfection (N. 232).
Some of the double stars have very long periods, such as ς Coronæ, where the revolving star takes 737 years nearly to accomplish a circuit. Others again have very short periods, as η Coronæ, ζ Cancri, and ξ Ursæ Majoris, whose periodic times are 42·500, 58·91, and 58·26 years respectively: therefore each of these has performed more than one entire revolution since their motions were observed. ζ Herculis, whose periodic time is only about 301⁄4 years, has accomplished two complete circuits, the lesser star having been eclipsed by the greater each time. The first of these two truly wonderful events, of one sun eclipsing another sun, was seen by Sir William Herschel in 1782.
The orbits and periodic times of so many of these binary systems having been determined proves beyond a doubt that sun revolves about sun in the starry firmament by the same law of gravitation that makes the earth and planets revolve about the sun (N. 232).
Since the parallax of 61 Cygni and that of α Centauri have been determined, Sir John Herschel has made the following approximation to the dimensions of their orbits and masses. The distance between the two stars of 61 Cygni, that is the radius vector of the revolving star, has hardly varied from 15ʺ·5 ever since the earliest observations; while in that time the star has moved through 50°; it is evident therefore that the orbit must be 399nearly circular. It is at right angles to the visual ray, and the periodic time is 514 years. The parallax or radius of the earth’s orbit as seen from the star is 0ʺ·348, while the radius of the star’s orbit as seen from the earth is 15ʺ·5; hence the radius of the star’s orbit is to that of the earth’s orbit as 15ʺ·5 to 0ʺ·348, or nearly as 45 to 1. So the orbit described by the two stars of 61 Cygni about one another greatly exceeds that which Neptune describes about the sun. Since the mean distance of the stars and their periodic time are given, the sum of the masses of the two stars is computed to be 0·3529, that of the sun being 1. Thus our sun is not vastly greater nor vastly less than the stars composing 61 Cygni, which is a small inconspicuous star to the naked eye, not exceeding the 6th magnitude.
Of all the double stars α Centauri is the most beautiful: it is the brightest star in the southern hemisphere, equal, if not superior, to Arcturus in lustre. The distance between the two stars has been decreasing at the rate of half a second annually since the year 1822, while the angular motion has undergone very little change, which shows that the plane of the orbit passes through the earth like the orbits of 44 Boötes, and π Serpentarii; that is to say, the edge of the orbit in these three stellar systems is presented to the earth, so that the revolving star seems to move in a straight line, and to oscillate on each side of its primary. Were this libration owing to parallax, it would be annual from the revolution of the earth about the sun; but as years elapse before it amounts to a sensible quantity, it can only arise from a real orbital motion seen obliquely. In this case five observations are sufficient for the determination of the orbit, provided they be exact; but the quantities to be measured are so minute, that it is only by a very long series of observations that accuracy can be attained. In 1834 Captain Jacob determined the periodic time of the revolving star of α Centauri to be 77 years, and the distance between the two to be 17ʺ·5; and since the decrease is half a second annually, the distance or radius vector of the revolving star was 12ʺ·5 in the year 1822; and as Mr. Henderson had determined the parallax or radius of the earth’s orbit as seen from the star to be ·913, it follows that the real semi-axis of the revolving star’s orbit is 131⁄2 times greater than the semi-axis of the earth’s orbit as a minimum. The real dimensions of the ellipse therefore cannot be so small as the orbit of Saturn, and may possibly 400exceed that of Uranus. It is very probable that an occultation of one of the suns by the other will take place in 1867, or a very close appulse of the two stars.
Singular anomalies have appeared in the motions of 70 Ophiuchi, which was discovered to be a binary system by Sir William Herschel in 1779, and which has since nearly accomplished a revolution. Various orbits have been computed: those which best represent the angles of position fail with regard to the distances of the stars from one another, and vice versâ. But it is a very remarkable fact that the errors are periodical, being for considerable periods of time alternately in excess and defect. Captain W. S. Jacob, who determined the periodic time of the revolving star to be 93 years, attributes this anomaly to the disturbing action of an opaque body revolving round the lesser star. Assuming that to be the case, and computing, he found that the errors were considerably diminished both in the angle of position and distance. It is a subject of the highest interest, and well worthy of the attention of such astronomers as have the means of making the necessary observations. Among the triple systems, as ζ Cancri, two of the stars revolve about one another in 58·9 years; but the motion of the third and most distant is so slow, that it has only accomplished a tenth part of its revolution about the other two since the system was discovered.
It appears from the calculations of Mr. Dunlop that ς Eridani accomplishes a revolution in little more than 30 years. The motion of Mercury is more rapid than that of any of the planets, being at the rate of 107,000 miles an hour. The perihelion velocity of the comet of 1680 was 880,000 miles an hour; but, if the two stars of ς Eridani, or of ξ Ursæ Majoris, be as remote from one another as the nearest fixed star is from the sun, the velocity of the revolving star must exceed the power of imagination to conceive. The elliptical motion of the double stars shows that gravitation is not confined to the planetary motions, but that systems of suns in the far distant regions of the universe are also obedient to its laws. The stellar systems present a kind of sidereal chronometer, by which the chronology of the heavens will be marked out to future ages by epochs of their own, liable to no fluctuations from such disturbances as take place in our system. Some stars are apparently double, though altogether unconnected, one being far behind the other in space, as α Lyræ, 401which apparently consists of two stars, one of the first, the other of the eleventh magnitude. Aldebaran, α Aquilæ, and Pollux are remarkable instances of these optically double stars. It has been shown how favourable that circumstance is for ascertaining the parallax of the nearest of the two. (N. 232.)
The double stars are of various hues: sometimes both stars are of the same colour, as in α Centauri and 61 Cygni, where the larger stars are of a bright orange and the smaller ones a deeper tint of the same, but they most frequently exhibit the contrasted colours. The large star is generally yellow, orange, or red; and the small star blue, purple, or green. Sometimes a white star is combined with a blue or a purple, and more rarely a red and white are united. In many cases these appearances are due to the influence of contrast on our judgment of colours. For example, in observing a double star, where the large one is a full ruby red, or almost blood colour, and the small one a fine green, the latter loses its colour when the former is hid by the cross wires of the telescope. That is the case with γ Andromedæ, which is a triple star, the small one, which appears green, being closely double. ι Cancri is an instance of a large yellow star and a small one which appears blue by contrast. Still there are a vast number where the colours are decidedly different, and suggest the curious idea of two suns, a red and a green, or a yellow and a blue, so that a planet circulating round one of them may have the variety of a red day and a green day, a yellow day and a blue day. Sir John Herschel observes, in one of his papers in the Philosophical Transactions, as a very remarkable fact, that, although red stars are common enough, no example of a solitary blue, green, or purple star has yet been produced.
Sirius is the only star on record whose colour has changed. In the time of Ptolemy it was red; now it is one of the whitest stars in the heavens.
M. Struve has found that, out of 596 bright double stars, 375 pairs have the same intensity of light and colour; 101 pairs have different intensity, but the same colour; and 120 pairs have the colours of the two stars decidedly different.
Certain rays, which exist in the sun’s light, are wanting in the spectra of every coloured star, and probably never existed in the light of these stars, as there is no reason to believe that they are absorbed by the stars’ atmosphere, though they may be by 402the earth’s. There are no defective rays in the white light of Sirius, Procyon, and others; but Sir David Brewster found in the spectrum of the orange-coloured light of ζ Herculis a defective band in the red space, and two or more in the blue; consequently, the orange colour of the star is owing to a want of blue rays; for flames in which certain rays are wanting take the colour of the predominating rays. If the black rays in the solar spectrum were owing to the absorption of the sun’s atmosphere, the light from the margin of his disc, having to pass through a greater thickness of it, would exhibit deeper lines than that which comes from his centre; but, as no difference is perceptible, it may be inferred that the analogous bands in the light of the coloured stars are not due to the absorption of their atmospheres, but that they arise from the different kinds of combustion by which these bodies are lighted up.
All the ordinary methods fail for finding the parallax when the distances of the stars are very great. An angle even of one or two seconds, viewed in the focus of our largest telescopes, does not equal the thickness of a spider’s thread, which makes it impossible to measure such minute quantities with any degree of accuracy. In some cases, however, the binary systems of stars furnish a method of estimating an angle of even the tenth of a second, which is thirty times more accurate than by any other means. From them the actual distances of some of the more remote stars will ultimately be known.
Suppose that one star revolves round another in an orbit which is so obliquely seen from the earth as to look like an ellipse in a horizontal position, then it is clear that one-half of the orbit will be nearer to us than the other half. Now, in consequence of the time which light takes to travel, we always see the satellite star in a place which it has already left. Hence, when that star sets out from the point of its orbit which is nearest to us, its light will take more and more time to come to us in proportion as the star moves round to the most distant point in its orbit. On that account the star will appear to us to take more time in moving through that half of its orbit than it really does. Exactly the contrary takes place on the other half; for the light will take less and less time to arrive at the earth in proportion as the star approaches nearer to us; and therefore it will seem to move through this half of its orbit in less time than it really does. 403This circumstance furnishes the means of finding the absolute breadth of the orbit in miles, and from that the true distance of the star from the earth. For, since the greatest and least distances of the satellite star from the earth differ by the breadth of its orbit, the time which the star takes to move from the nearest to the remotest point of its orbit is greater than it ought to be by the whole time its light takes to cross the orbit, and the period of moving through the other half is exactly as much less. Hence the difference between the observed times of these two semi-revolutions of the star is equal to twice the time that its light employs to cross its orbit; and, as we know the velocity of light, the diameter of the orbit may be found in miles, and from that its whole dimensions; for the position of the orbit with regard to us is known by observation, as well as the place, inclination, and apparent magnitude of its major axis, or, which is the same thing, the angle under which it is seen from the earth. Since, then, three things are known in this great triangle, namely, the base or major axis of the orbit in miles, the angle opposite to it at the earth, and the angle it makes with the visual ray, the distance of the satellite star from the earth may be found by the most simple of calculations. The merit of having first proposed this very ingenious method of finding the distance of the stars is due to M. Savary; but, unfortunately, it is not of general application, as it depends upon the position of the orbit, and a long time must elapse before observation can furnish data, since the shortest period of any revolving star that we know of is 30 years. Still the distances of a vast number of stars may ultimately be made out in this way; and, as one important discovery almost always leads to another, their masses may thus be weighed against that of the earth or sun.
The only data employed for finding the mass of the earth, as compared with that of the sun, are, the angular motion of our globe round the sun in a second of time, and the distance of the earth from the sun in miles (N. 233). Now, by observations of the binary systems, we know the angular velocity of the small star round the great one; and, when we know the distance between the two stars in miles, it will be easy to compute how many miles the small star would fall through by the attraction of the great one in a second of time. A comparison of this space with the space through which the earth would descend towards 404the sun in a second will give the ratio of the mass of the great star to that of the sun or earth. According to M. Bessel, the weight of the two stars of 61 Cygni is equal to half the weight of the sun. Little as we know of the absolute magnitude of the fixed stars, the quantity of light emitted by many of them shows that they must be much larger than the sun. Dr. Wollaston determined the approximate ratio which the light of a wax candle bears to that of the sun, moon, and stars, by comparing their respective images reflected from small glass globes filled with mercury, whence a comparison was established between the quantities of light emitted by the celestial bodies themselves. By this method he found that the light of α Lyræ is five and a half times greater than that of the sun. Sir John Herschel reflected the moon’s light totally by a prism, which, concentrated by a lens, was compared directly with that of α Centauri. After making allowance for the quantity of the moon’s light lost in passing through the lens and prism, he found that the mean quantity of light sent to the earth by a full moon exceeds that sent by α Centauri in the proportion of 27,408 to 1. Now, Dr. Wollaston found the proportion of the sun’s light to that of the full moon to be that of 801,072 to 1. Hence, the light sent to us by the sun is to that sent by α Centauri as about twenty-two thousand millions to one. But, as the parallax of α Centauri is 1ʺ, it really is two and a half times brighter than the sun. The light of Sirius is four times that of α Centauri, but its parallax is only 0ʺ·230: hence it has an intrinsic splendour 63·02 times that of our luminary. It is therefore estimated to be a hundred times as large; so that, were Sirius in the earth’s place, its surface would extend 150 times as far as the orbit of the moon. The light of Sirius, according to the observations of Sir John Herschel, is 324 times greater than that of a star of the sixth magnitude; if we suppose the two to be really of the same size, their distances from us must be in the ratio of 57·3 to 1, because light diminishes as the square of the distance of the luminous body increases.
So many of the stars have proper motions altogether independent of the annual rotation of the earth in its orbit, that it may be doubted whether there be such a thing as a fixed star. Groombridge is the most rapid known: it has a proper motion of 7ʺ of arc annually; α Centauri moves at the rate of 3ʺ·58 annually, 405and 61 Cygni describes a line in space of 5ʺ·12 in the same time. These motions are probably in curves, but at the distance of the earth they will appear to be rectilineal for ages to come. The motion of little more than five seconds of space, which 61 Cygni describes annually, seems to us to be extremely small; but at the distance of that star an angle of one second corresponds to twenty-four millions of millions of miles; consequently the annual motion of 61 Cygni is 120 millions of millions of miles, and yet, as M. Arago observes, we call it a fixed star. From the same cause it is evident that the crowding of the stars in the Milky Way may be apparent only, and that the stars may be at vast distances from one another, and no doubt are.
Were the solar system and the whole of the stars visible to us carried forward in space by a motion common to all, like ships drifting in a current, it would be impossible for us, moving with the rest, to ascertain its direction. Sir William Herschel perceived that a great part of the motions of the stars is only apparent, arising from a real motion of the sun in a contrary direction. Among many discrepancies he found that the stars in the northern hemisphere have a general tendency to move towards a point diametrically opposite to λ Herculis, which he attributed to a motion of the solar system in a contrary direction. For it was evident to him, that the stars, from the effects of perspective alone, would seem to diverge in the direction to which the solar system was going, and would converge towards the space it had left, and that there would be a regularity in these apparent motions which would hereafter be detected. Since Sir William Herschel’s time the proper motions of the stars have been determined with much greater accuracy, and many have been added to the list by comparing the ancient and modern tables of their places; his views have been established by four of the greatest astronomers of the age, MM. Lundahles, Argelander, Otto Struve, and Peters, who have clearly proved the motion of the sun from that of the stars in the northern hemisphere, and Mr. Galloway has come to the same conclusion from the motions of the stars in the southern hemisphere (N. 234). The result is, that the sun, accompanied by all his attendant planets, is moving at the rate of 422,424 miles—or over a space nearly equal to his own diameter—in the course of a day, and that the motion is 406directed towards a point in a line joining the two stars μ and π Herculis at a quarter of the apparent distance of these two stars, reckoning from π Herculis. This investigation was founded upon no law assumed or observed, such as the circulation of all the stars of our firmament about a common centre, though philosophers have speculated as to the probability of such a motion in the sun and stars in the plane of the Milky Way. Should the sun and his stellar companions be moving in a nearly circular orbit, the centre of motion would be in the plane passing through the sun perpendicular to the direction of his motion. The constellations through which that great circle would pass are Pisces, Australis, Pegasus, Andromeda, Perseus, &c. M. Argelander is of opinion that the sun’s orbit is nearly in the plane of the Milky Way, and, therefore, that its centre must probably be in Perseus, while M. Mädler places it in the Pleiades, which seems to be inadmissible; but the data are too uncertain at present to admit of any absolute conclusion as to the sun’s orbit and the general motion of the stellar firmament: for though the stars in every region of the sky tend towards a point in Hercules, it is not yet known whether their motions are uniform or variable, whether the sun’s motion be gradually changing, and whether the stars form different independent systems, each having its own centre of attraction, or if all obey one powerful controlling force which pervades the whole universe. Accurate observations of the places of a select number of stars of all dimensions in the Milky Way continued for a series of years would no doubt decide this point.
The proper motion of a star combined with the progressive velocity of light alters the apparent periodic time of the revolving star of a binary system. If the orbit of a double star be at right angles to the visual ray, and both the sun and the star at rest, the periodic time of the revolving star, say of 10,000 days, would always be the same. But if the centre of gravity of the star were to recede in a direct line from the sun with the velocity of one tenth of the radius of the earth’s orbit in a day, then at the end of 10,000 days it would be more remote from us by 1000 of such radii—a space light would take 57 days to traverse: hence, although the periodic time of the star would really be the same, the completion of its period would only be known to us 57 days after it had taken place, so that the periodic time would 407appear to us to be 10,057 days instead of 10,000. Were the star to approach to the sun by the same quantity instead of receding, the apparent periodic time would be diminished by 57 days.
As the sun is only a unit in the stellar system, so the Milky Way, and all the stars that adorn the firmament of both hemispheres, constitute a group which is but a unit among the infinite numbers of starry clusters and nebulæ that are profusely scattered throughout the universe.
By the aid of a good telescope there may be seen on the clear vault of heaven, between the stars of our own stellar system, and far in the depths of space, an immense multitude of objects like comets or clouds of white vapour of all forms and sizes. Some are mixed with stars, others are entirely formed of them. Many appear as if they were stellar, but required a telescope of higher power to resolve them, and vast numbers appear to be matter rarefied in the highest possible degree, giving no indication of a stellar nature; and these are in every state of condensation, from a vague film hardly to be discerned to such as have actually arrived at a solid nucleus of stars. The cloudy appearance is merely the blending of the rays of innumerable stars which are themselves invisible from their extreme distance, like parts of the Milky Way. Sir William Herschel was at first of that opinion, and the nebulæ that have been resolved by Lord Rosse’s telescope have led astronomers to believe that such is the case. Yet the tails of comets, the zodiacal light, and the extensive luminous atmospheres which encompass many of the stars, show that, in all probability, a self-luminous phosphorescent material substance in a highly diluted or gaseous form exists in vast abundance.
The number of the nebulæ, like that of the stars, is only limited by the imperfection of our instruments, for each improvement in the telescope only enables us to penetrate a little farther into the infinity of space—to see a few more of these shadowy existences in the far distance, and to resolve a few more of those that are comparatively near. Sir William Herschel examined the nature and determined the position of 2500 nebulæ in the northern hemisphere whose places were computed from his observations, reduced to a common epoch, and arranged into a catalogue, in order of right ascension, by his sister, Miss Caroline Herschel, who added lustre to the name she bore by her eminence in astronomical knowledge and discovery. Sir John Herschel revised 408his father’s observations, and added 800 nebulæ to the catalogue before he went to the Cape of Good Hope, in order to complete the survey of the heavens. On his return he published a catalogue of 2049 nebulæ of the southern hemisphere, of which 500 were previously unknown, with their position in the heavens. In a work unparalleled for elegance of style, depth of knowledge, and originality of views, he has given engravings from his drawings of the most remarkable objects, so that whatever changes may take place in their form, place, or condensation, will be known by astronomers of future ages.
Though infinite in variety, the nebulæ are of two distinct classes; one consists of patches of great dimensions, capriciously irregular, assuming all the fantastic forms of clouds, now bright, now obscure; sometimes like vapour flying before the wind; sometimes stretching long arms into space. Many present an ill-defined surface, in which it is difficult to say where the centre of the greatest brightness is. Large portions are resolvable into stars; many have a granulated appearance, as if they were resolvable; and others probably are not so merely from the smallness and closeness of the stars, and possibly from their remoteness, indicating the complex and irregular form the Milky Way would present if seen from a distance. A wonderful nebula of this kind is visible to the naked eye in the constellation of Orion; it is of vast extent, sending branches even into the southern hemisphere; and, although Lord Rosse’s telescope has resolved much that had hitherto resisted others, there are parts that still maintain their nebulous appearance from extreme remoteness, presenting a kind of mottled aspect, like flocks or wisps of wool, or mackerel sky. There can be no doubt of its being an unfathomable congeries of stars, which there is reason to believe has changed its form in some parts within the last fifty years. Vast multitudes of nebulæ of this kind are so faint as to be with difficulty discerned at all till they have been for some time in the field of the telescope, or are just about to quit it. Occasionally they are so vague, that the eye is conscious of something being present, without being able to define what it is; but the unchangeableness of its position convinces the mind that it is a real object—“an image was before mine eyes, but I could not discern the form thereof.”
No drawing can give an idea of the boundaries of such nebulæ 409as that of Orion; even with Lord Rosse’s telescope the edges either fade into a luminous mist, which becomes more rare till it is imperceptible, or end in a tissue of faintish flocculi, or in filaments which become finer and more scattered till they cease to be visible, showing that the real boundaries have not been seen.
The other class of nebulæ, vastly inferior in size, of definite forms and great variety of character, are scattered through the remote heavens, or congregated in a great nebulous district far from the Milky Way. Many cling to stars like wisps of clouds, others are exactly like comets with comæ and tails; but the most definite forms are annular and lenticular nebulæ, nebulous stars, planetary and elliptical nebulæ, and starry clusters. However, there are two in the northern hemisphere differing from all of these, which are described by Sir John Herschel as amazing objects. One in Vulpecula is like an hourglass or dumb bell of bright matter, surrounded by a thin hazy atmosphere so as to give the whole an oval form, or the appearance of an oblate spheroid; with a higher optical power its form is much the same, but the brighter part is resolved into stars, and the hazy part, though still nebulous, assumes that mottled appearance which shows that the whole is a stellar system of the most peculiar structure: it is a phenomenon that bears no resemblance to any known object. (Fig. 3, plate 8, and fig. 3, plate 9). The other is indeed most wonderful, and its history shows the gradual increase in the space-penetrating power of telescopes. To Messier it appeared merely to be a double nebula with stars; with Sir William Herschel’s telescope it presented the appearance of a bright round nebula encompassed at a little distance by a halo or glory, and accompanied by a companion; while in Sir John Herschel’s 20 feet reflector it appeared to “consist of a bright round nucleus, surrounded at a distance by a nebulous ring split through half its circumference, and having the split portions separated at an angle of 45 degrees each to the plane of the other.” (Fig. 1, plate 10.) This nebula appeared to Sir John to “bear a strong similitude to the Milky Way, suggesting the idea of a brother system bearing a real physical resemblance and strong analogy of structure to our own.”
This object, which disclosed to Lord Rosse the astonishing phenomenon of spiral nebulæ seen in his telescope, presents the appearance of the fig. 1 in plate 10, in which the partial 410division of the limb of the ring into two branches is at once recognised in the bright convolutions of the spiral. The outlying nebula is connected by a narrow curved band of light with the ring; the whole is either resolved into stars, or evidently might be with a still higher optical power. With regard to the marvellous nebula in question Lord Rosse observes, that “with each increase of optical power the structure has become more complicated, and more unlike anything that could result from any form of a dynamical law of which we find a counterpart in our system. The connection of the companion with this great nebula, of which there is not the least doubt, adds to the difficulty of forming any hypothesis. It is impossible that such a system could exist without internal movement, to which may be added a resisting medium; but it cannot be regarded as a case of mere static equilibrium.” This is by no means the only instance of a spiral nebula; Lord Rosse has discovered several others: some are easily seen—others require the highest powers of his telescope. From the numerous offsets that branch from the Milky Way and run far into space, it may possibly partake also of the spiral form.
There are seven annular nebulæ in the northern hemisphere, since Lord Rosse has discovered that five of the planetary nebulæ belong to this class. One of the finest examples of an annular nebula is to be seen midway between β and γ Lyræ (fig. 2, plate 9). According to Sir John Herschel, it is elliptical in the ratio of 4 to 5, and is sharply defined—the internal opening occupying about half the diameter. This opening is not entirely dark, but filled with a faint hazy light like fine gauze stretched over a hoop. Its diameter, if it is as far from us as 61 Cygni, must be 1300 times greater than the diameter of the earth’s orbit—dimensions that are most astounding. Lord Rosse’s telescope resolves this object into stars of extreme minuteness, with filaments of stars adhering to its edges and a pretty bright star in its interior. These rings are like hollow shells whose borders seem brighter because the nebulous substance, whatever it may be, is more condensed to appearance than the central part. The other annular nebula in the northern hemisphere described by Sir John Herschel is a small faint object, and more easily resolvable into stars. One of the annular nebulæ seen by Lord Rosse is surrounded by a faint external flat ring; another has ansæ, as if an annular nebulous ring encompassed it and was foreshortened. Two annular nebulæ 411have perforations as if the black sky was seen through openings in the interior haze, for in no instance is the central opening quite dark.
Some nebulæ are like very elliptical annular systems seen obliquely. If they be elliptical flat rings, the dark centre may be a real opening; but should the systems be a series of very long elliptical concentric shells surrounding a hollow, the dark axis may be merely a line of comparative darkness.
The connection of the elliptical nebulæ with double stars is mentioned as very remarkable. In one elliptical nebula whose longer axis is 50ʺ there are two individuals of a double star each of the 10th magnitude symmetrically placed rather nearer the vertex of the ellipse than the foci; in another the stars are unequal, but placed exactly at the extremities of the major axis, as in plate 8: besides these there are several other instances.
Double nebulæ are not unfrequent in both hemispheres, exhibiting all the varieties of distance, position, and relative brightness, with their counterparts the double stars. The rarity of single nebulæ as large, faint, and as little condensed in the centre as these, makes it extremely improbable that two such bodies should be accidentally so near as to touch, and often in part to overlap each other, as these do. It is much more likely that they constitute systems; and, if so, it will form an interesting object of future inquiry to discover whether they possess orbital motion.
Nebulous stars are beautiful objects, quite different from all the preceding. They are round or oval, increasing in density towards the centre. Sometimes the central matter is so vividly and sharply condensed and defined that the nebula might be taken for a bright star surrounded by a thin atmosphere. One is a star of the 8th magnitude exactly in the centre of a round bright atmosphere 25ʺ in diameter; the star is quite stellar, and not a nucleus: it has not the smallest appearance of being resolvable. Another nebulous star is ι Orionis, which has a broad atmosphere in which is a dark cavity not symmetrical with the star, and a small double star with a similar opening on the edge of the atmosphere. Lord Rosse observes that these openings appear to be of the same nature with that within the bright stars in the trapezium of Orion, the stars being at its edge; and he is convinced that the stars are not only connected with the nebula, but that they are equidistant with it; hence, if their parallax can be 412found, the distance of this nebula would be determined. The zodiacal light or lenticular shaped luminous haze surrounding the sun which may be seen extending beyond the orbits of Mercury and Venus soon after sunset in the months of April and May, or before dawn in November and December, seems to place our luminary in the class of nebulous stars. The extensive and delicate atmosphere of these nebulous stars assumes all degrees of ellipticity, from the circular to the spindle-shaped ray, or almost the right line.
Planetary nebulæ have exactly the appearance of planets with round or oval discs, sometimes sharply terminated, at other times hazy and ill-defined. Their surface, which is blue or blueish white, is equable or slightly mottled, and their light occasionally rivals that of the planets in vividness. They are generally attended by minute stars, which give the idea of accompanying satellites. These nebulæ are of enormous dimensions. One near γ Aquarii has a sensible diameter of about twenty seconds, and another presents a diameter of twelve. Sir John Herschel has computed that, if these objects be as far from us as the stars, their real magnitude, on the lowest estimation, must be such as would fill the orbit of Uranus. He concludes that, if they be solid bodies of a solar nature, their intrinsic splendour must be far inferior to that of the sun, because a circular portion of the sun’s disc subtending an angle of twenty seconds would give a light equal to that of a hundred full moons; while, on the contrary, the objects in question are hardly, if at all, visible to the naked eye. From the uniformity of the discs of these planetary nebulæ, and their apparent want of condensation, he presumes that they may be hollow shells emitting light from their surface only. The southern hemisphere is very rich in them, where twenty-eight or twenty-nine have been discovered, some in the midst of a cluster of stars, with which they form a beautiful contrast. Three are of a decided blue colour, one Prussian blue, or verditer green, the other two of a bright sky blue, of great beauty and delicacy. One seems to belong to the class of double nebulæ or double stellar nebulæ of the utmost remoteness. Since Lord Rosse’s telescope has shown that five of the planetary nebulæ are annular, some of those in the southern hemisphere may ultimately be found to belong to the same class.
Probably nine tenths at least of the nebulous contents of the 413heavens consist of spherical or elliptical forms presenting every variety of elongation and central condensation. Of these a great number have been resolved into stars, and a great many present that mottled appearance which renders it certain that an increase of optical power would decompose them. Those which resist do so on account of the smallness and closeness of the stars of which they consist.
Elliptical nebulæ are very common; by much the finest may be seen near the star υ in the girdle of Andromeda. It is visible to the naked eye, and has frequently been taken for a comet. With a low optical power it has the spindle-shaped form of fig. 6, plate 5, the brightness being at first gradually and then rapidly condensed towards the centre, so that it has been compared to a star shining through horn, but had never appeared resolvable even with high optical powers till Mr. Bond examined it at the observatory of Cambridge in the United States. He found that its brightness extends over 21⁄2 degrees in length, and more than a degree in breadth, including two small adjacent nebulæ, so that it is oval. It is strongly and rapidly condensed into a nucleus on its northern side; and although it was not all resolved, it was seen to be strewed over with star dust, or extremely minute visible stars, which leaves not a doubt of its being a starry system. The most remarkable part of Mr. Bond’s discovery are two very narrow dark lines which extend along one side of the oval parallel to its major axis. These black streaks, difficult to distinguish, indicate a stratified structure, and are not the only instance of that arrangement in nebulæ. Fig. 1, in plate 9, is from Mr. Bond’s drawing of this nebula.
Multitudes of nebulæ appear to the unassisted eye, or are seen with ordinary telescopes, like round comets without tails; but when viewed with powerful instruments they convey the idea of a globular space, insulated in the heavens and full of stars, constituting a family or society apart from the rest, subject only to its own internal laws. To attempt to count the stars in one of these globular clusters, Sir John Herschel says, would be a vain task; they are not to be reckoned by hundreds. On a rough computation, it appears that many clusters of this description must contain ten or twenty thousand stars compacted and wedged together in a round space, whose apparent area is not more than a tenth part of that covered by the moon; so that its centre, 414where the stars are seen projected on each other, is one blaze of light. If each of these stars be a sun, and if they be separated by intervals equal to that which separates our sun from the nearest fixed star, the distance which renders the whole cluster barely visible to the naked eye must be so great, that the existence of such a splendid assemblage can only be known to us by light which must have left it at least a thousand years ago. These magnificent globular or spheroidal aggregates of stars are so arranged that the interior strata are more crowded and become more nearly spherical as they approach the centre. A most splendid object of this nature may be seen in the constellation Hercules (N. 235).
Of 131 of these magnificent objects in the southern hemisphere, two of them are pre-eminently splendid. The globular cluster of α Centauri is beyond comparison the finest of its kind: it is perfectly spherical, and occupies a quarter of a square degree; the stars in it are literally innumerable, crowding and densely aggregated towards the centre; and, as its light is not more to the naked eye than that of a star of the 4th or 5th magnitude, their minuteness is extreme. It has a dark hole in its centre, with a bridge of stars across,—a circumstance peculiar to this cluster.
Lacaille’s globular cluster, or 47 Toucani, is completely insulated in a very dark part of the sky not far from the lesser of the Magellanic clouds. The stars, which are of the 14th magnitude, immensely numerous, compressed and white, form three distinct stages round a centre, where they suddenly change in hue, and form a blaze of rose-coloured light. One cluster consists of large ruddy stars and small white ones; another of greater beauty consists of shells or coats of stars of the 11th and 15th magnitude. There are thirty globular clusters of extreme beauty collected within a circular space of not more than eighteen degrees radius, which lies in the part of the sky occupied by the constellations Corona Australis, the body and head of Sagittarius, the tail of Scorpio, part of Telescopium and Ara. The Milky Way passes diametrically across the circular area in question, which gives prodigious brilliancy to this part of the sky. For besides these globular clusters, which all lie in the starry part, and not in the dark spaces, there are the only two annular nebulæ known to exist in the southern hemisphere. No part of the heavens is fuller of objects beautiful and remarkable in themselves, and rendered 415still more so by their mode of association, and by the peculiar features assumed by the Milky Way, which are without a parallel for richness and magnificence in any other part of the sky. Some of the globular clusters are so remote that the stars are scarcely discernible—mere star dust. There is a double globular cluster in the southern hemisphere of very small dimensions, separated by a minute interval,—a combination which suggests the idea of a globular cluster revolving about a very oblate spheroidal one in the plane of the equator, and in an orbit which is circular, and seen obliquely like the central nebula itself, with a diameter somewhat more than four times the latter,—a stupendous system doubtless, but of which the reality can hardly be supposed improbable.
There appears to be some connexion between ellipticity of form and difficulty of resolution, for spherical clusters are in general easily resolved into their component stars, while there is scarcely an instance of an elliptical cluster yielding except to a very high optical power. Vast masses of the nebulæ have never been resolved. Lord Rosse’s great telescope has resolved parts of the nebula of Orion, and various others which had not yielded to instruments of less power; it enables the astronomer to penetrate farther into space, and shows objects with greater clearness, than any other. But, excellent as this instrument is, thousands of nebulæ are not to be resolved even by it. Those who imagine that any work of man can resolve all the nebulous matter in the heavens must have a very limited idea of the extent and sublimity of creation.
Innumerable nebulæ in both hemispheres take the form of clusters of stars, but are totally different from the globular clusters, inasmuch as they are of irregular form and follow no uniform law of condensation. The Pleiades is an instance in our own stellar system; for although only 7 or 8 stars are visible to the naked eye, telescopes show that more than 200 belong to the group. In the constellation Cancer there is a luminous spot called the Præsepe or Beehive, which a very low power resolves into stars; and the constellation Coma Berenices is another stellar group. Many are of exquisite beauty, as that round α Crucis, which, though consisting of only a hundred and ten stars, is like a piece of fancy jewellery, from the colours of the stars, which are greenish white, green, blueish green, and red. Many of these 416clusters contain thousands of stars, and are frequently in the poorer parts of the sky, as if in the course of ages the stars had been attracted towards a centre.
The existence of every degree of ellipticity in the nebulæ—from long lenticular rays to the exact circular form—and of every shade of central condensation, from the slightest increase of density to apparently a solid nucleus—may be accounted for by supposing the general constitutions of those nebulæ to be that of oblate spheroidal masses of every degree of flatness from the sphere to the disc, and of every variety in their density and ellipticity towards the centre. It would be erroneous, however, to imagine that the forms of these systems are maintained by forces identical with those already described, which determine the form of a fluid mass in rotation; because, if the nebulæ be only clusters of separate stars, as in the greater number of cases there is every reason to believe them to be, no pressure can be propagated through them. Consequently, since no general rotation of such a system as one mass can be supposed, it may be conceived to be a quiescent form, comprising within its limits an indefinite number of stars, each of which may be moving in an orbit about the common centre of the whole, in virtue of a law of internal gravitation resulting from the compound gravitation of all its parts. Sir John Herschel has proved that the existence of such a system is not inconsistent with the law of gravitation under certain conditions.
The distribution of the nebulæ over the heavens is even more irregular than that of the stars. In some places they are so crowded together as scarcely to allow one to pass through the field of the telescope before another appears, while in other parts hours elapse without a single nebula occurring. They are in general only to be seen with the best telescopes, and are most abundant in a zone whose general direction is not far from the hour circles 0h and 12h, and which crosses the Milky Way nearly at right angles. Where that nebulous zone passes over the constellations Virgo, Coma Berenices, and the Great Bear, they are to be found in multitudes.
The nebulous system is nearly divided into two parts by the Milky Way. One-third of the whole visible nebulous contents of the heavens forms a broad irregular mass, interspersed with vacant intervals, which fills about an eighth of the surface of the 417northern hemisphere. It occupies the constellations Leo, Leo Minor, the body, tail, and hind legs of Ursa Major, the nose of Camelopard, the point of the tail of Draco, Canis Venatica, Coma Berenices, the preceding leg of Boötes, and the head, wings, and shoulder of Virgo, which is the richest part. There is a lesser nebulous region in this hemisphere, but entirely separated from the preceding, which occupies the chest and wing of Pegasus, the constellations Pisces and Andromeda. If we could imagine the ring or zone of the Milky Way to encircle or coincide with the horizon, the great nebulous mass would form a canopy over head, descending down to a considerable distance on all sides, chiefly towards the north pole; and the richest part, which is in Virgo, would then be directly over head in the north pole of the Milky Way, that is in 12h 47m right ascension, and 64° north polar distance.
With the exception of the Magellanic clouds, there is a much greater uniformity in the distribution of the nebulæ in the southern hemisphere than in the northern. They are separated by spaces of vacuity of greater or less dimensions. One of these barren regions extends for nearly fifteen degrees all around the south pole, and close on its border; the lesser of the Magellanic clouds occurs completely insulated; while the greater Magellanic cloud is in connexion with something approaching to a zone of connected nebulous patches which extends along the back of Doradus, through a portion of Horologium and Eridanus, part of Fornix, and over the paws of Cetus to the equator, where it unites with the nebulous regions of Pisces.
The Magellanic clouds form two of the most striking features in the southern hemisphere; both of these nebulæ are visible to the unassisted eye, being nearly of the same intensity as the brighter portions of the Milky Way; but the smaller is entirely effaced by moonlight, and the larger nearly so. They are altogether unconnected with the Milky Way and with one another. The Nubecula Major is far superior to the Nubecula Minor in every respect, though they are similar in internal structure. The former consists of large tracts and ill-defined patches of irresolvable nebulæ, and nebulosity in every stage of resolution, up to perfectly resolved stars like the Milky Way; and also of regular and irregular nebulæ, properly so called; of globular clusters in every stage of resolvability; and of clustering groups sufficiently 418insulated and condensed to come under the designation of clusters of stars. Of these the nebula known as Lacaille’s 30 Doradus is too remarkable to be passed over. It is very large, situate within the Nubecula Major, and consists of an assemblage of nearly circular loops uniting in a centre, in or near which there is a circular black hole. In short, for the number and variety of the objects, there is nothing like this cloud. Within an area of only forty-two square degrees, Sir John Herschel has determined the places, and registered 278 nebulæ and clusters of stars, with fifty or sixty in outlying members immediately adjacent. Even the most crowded parts of the stratum of Virgo, in the wing of that constellation, or in Coma Berenices, offer nothing approaching to it. It is evident, from the intermixture of stars and unresolved nebulosity, which probably might be resolved with a higher optical power, that the nubeculæ are to be regarded as systems sui generis, to which there is nothing analogous in our hemisphere.
Next to the Magellanic clouds the great nebula round η Argûs is one of the most wonderful objects of the southern sky. It is situate in that part of the Milky Way which lies between the Centaur and the body of Argus, in the midst of one of those rich and brilliant masses, a succession of which is so curiously contrasted with the profoundly dark adjacent spaces, and surrounded by one of the most beautiful parts of the southern heavens. Sir John Herschel says: “It would be impossible, by verbal description, to give any just idea of the capricious forms and irregular gradations of light affected by the different branches and appendages of this nebula. Nor is it easy for language to convey a full impression of the beauty and sublimity of the spectacle it offers when viewed in a sweep, ushered in as it is by so glorious and innumerable a procession of stars, to which it forms a sort of climax, justifying expressions which, though I find them written in my journal in the excitement of the moment, would be thought extravagant if transferred to these pages. In fact, it is impossible for any one, with the least spark of astronomical enthusiasm about him, to pass soberly in review with a powerful telescope, and on a fine night, that portion of the southern sky which is comprised between the 6th and 13th degrees of right ascension, and from 146° to 149° of north polar distance; such are the variety and interest of the objects he will encounter, and 419such the dazzling richness of the starry ground on which they are represented to his gaze.” In that portion of the sky there are many fine double stars—rich starry clusters; the elegant cluster of variously coloured stars round κ Crucis; a large planetary nebula with a satellite star; another of a bright blue colour, exquisitely beautiful and unique; and, lastly, η Argûs itself, the most extraordinary instance of a variable star in astronomical history.
It frequently occurred, during Sir John Herschel’s survey of the southern heavens, that some parts of the sky were noted for deeper blackness than others, and no stars could be seen; it frequently happened that far from the Milky Way, or any large nebula or cluster of stars, there were some indications of very remote branches of the Milky Way, or of an independent sidereal system or systems, bearing a resemblance to such branches. These were indicated by an exceedingly delicate and uniform dotting or stippling of the sky by points of light too small to admit of any one of them being steadily and fixedly viewed, and too numerous to be counted even if possible to view them. The truth of this existence was felt at the moment of observation; but the conviction, though often renewed, was not permanent. The places where these appearances occurred are given, in order that those who wish to verify them may have it in their power.
Such is a brief account of a very few of the discoveries contained in Sir John Herschel’s great work on the Nebulæ and other Phenomena of the Southern Hemisphere,—a work which will rise in estimation with the lapse of years. No doubt the form and internal structure of many of these nebulæ will be changed by telescopes of higher power; but as the places of the leading phenomena have been determined, the date of that great work may be regarded as the epoch of nebular time whence the relative changes that take place in the most distant regions of the universe will be estimated for ages to come; and in the inimitable writings of the highly gifted father and son the reader will find these subjects treated of in a style worthy of it and of them. Of late years the excellence of the instruments, and still more of the astronomers, in the foreign observatories, have aided the progress of sidereal astronomy immensely. Nor has it been cultivated with less success in our home and colonial establishments: certainly one of the most remarkable features of the times is the 420number of private observatories, built and furnished with the best instruments by private gentlemen, whose zeal has been rewarded by eminent success in all departments of the science. (N. 236.)
So numerous are the objects which meet our view in the heavens, that we cannot imagine a point of space where some light would not strike the eye;—innumerable stars, thousands of double and multiple systems, clusters in one blaze with their tens of thousands of stars, and the nebulæ amazing us by the strangeness of their forms and the incomprehensibility of their nature, till at last, from the limit of our senses, even these thin and airy phantoms vanish in the distance. If such remote bodies shone by reflected light, we should be unconscious of their existence. Each star must then be a sun, and may be presumed to have its system of planets, satellites, and comets, like our own; and, for aught we know, myriads of bodies may be wandering in space unseen by us, of whose nature we can form no idea, and still less of the part they perform in the economy of the universe. Even in our own system, or at its farthest limits, minute bodies may be revolving like the telescopic planets, which are so small that their masses have hitherto been inappreciable, and there may be many still smaller. Nor is this an unwarranted presumption; many such do come within the sphere of the earth’s attraction, are ignited by the velocity with which they pass through the atmosphere, but leave no residuum. These, which are known as falling stars and meteors, are periodical; but that is by no means the case with aërolites, which are also ignited by the sudden condensation of the air on entering our atmosphere, and are precipitated in solid masses with such violence on the earth’s surface that they are often deeply buried in the ground.
The fall of meteoric stones is much more frequent than is generally believed. Hardly a year passes without some instances occurring; and, if it be considered that only a small part of the earth is inhabited, it may be presumed that numbers fall in the ocean, or on the uninhabited part of the land, unseen by man. They are sometimes of great magnitude; the volume of several has exceeded that of the planet Ceres, which is about 70 miles in diameter. One which passed within 25 miles of us was estimated to weigh about 600,000 tons, and to move with a velocity of about 20 miles in a second; a fragment of it alone reached the earth. 421The obliquity of the descent of meteorites, the peculiar substances they are composed of, and the explosion accompanying their fall, show that they are foreign to our system; but whence derived is still a mystery.
Shooting stars and meteors burst from the clear azure sky, and, darting along the heavens, are extinguished without leaving any residuum except a vapour-like smoke, and generally without noise. Their parallax shows them to be very high in the atmosphere, sometimes even beyond its supposed limit, and the direction of their motion is for the most part diametrically opposite to the motion of the earth in its orbit. The astonishing multitudes of shooting stars and fire-balls that have appeared at stated periods over different parts of the globe, warrant the conclusion that there is either a nebula or that there are myriads of bodies revolving in groups round the sun which only become visible when inflamed by entering our atmosphere.
One of these nebulæ or groups seems to meet the earth in its annual revolution on the 12th and 13th of November.
On the morning of the 12th of November, 1799, thousands of shooting stars, mixed with large meteors, illuminated the heavens for many hours over the whole continent of America, from Brazil to Labrador: it extended to Greenland, and even Germany. Meteoric showers were seen off the coast of Spain, and in the Ohio country, on the morning of the 13th of November, 1831; and during many hours on the morning of the 13th November, 1832, prodigious multitudes of shooting stars and meteors fell at Mocha on the Red Sea, in the Atlantic, in Switzerland, and at many places in England. But by much the most splendid meteoric shower on record began at nine o’clock in the evening of the 12th of November, 1833, and lasted till sunrise next morning. It extended from Niagara and the northern lakes of America to the south of Jamaica, and from 61° of longitude in the Atlantic to 100° of longitude in central Mexico. Shooting stars and meteors, of the apparent size of Jupiter, Venus, and even the full moon, darted in myriads towards the horizon, as if every star in the heavens had started from their spheres. They are described as having been frequent as flakes of snow in a snow-storm, and to have been seen with equal brilliancy over the greater part of the continent of North America.
Those who witnessed this grand spectacle were surprised to 422see that every one of the luminous bodies, without exception, moved in lines which converged in one point in the heavens: none of them started from that point; but their paths, when traced backwards, met in it like rays in a focus, and the manner of their fall showed that they descended from it in nearly parallel straight lines towards the earth.
By far the most extraordinary part of the whole phenomenon is, that this radiant point was observed to remain stationary near the star γ Leonis for more than two hours and a half, which proved the source of the meteoric shower to be altogether independent of the earth’s rotation, and its parallax showed it to be far above the atmosphere.
As a body could not be actually at rest in that position, the group or nebula must either have been moving round the earth or the sun. Had it been moving about the earth, the course of the meteors would have been tangential to its surface; whereas they fell almost perpendicularly, so that the earth in its annual revolution must have met with the group. The bodies or the parts of the nebula that were nearest must have been attracted towards the earth by its gravity, and, as they were estimated to move at the rate of fourteen miles in a second, they must have taken fire on entering our atmosphere, and been consumed in their passage through it.
As all the circumstances of the phenomena were similar on the same day and during the same hours in 1832, and as extraordinary flights of shooting stars were seen at many places both in Europe and America on the 13th of November, 1834, 1835, and 1836, tending also from a fixed point in the constellation Leo, it has been conjectured, with much apparent probability, that this nebula or group of bodies performs its revolution round the sun in a period of about 182 days, in an elliptical orbit, whose major axis is 119 millions of miles; and that its aphelion distance, where it comes in contact with the earth’s atmosphere, is about 95 millions of miles, or nearly the same with the mean distance of the earth from the sun. This body must have met with disturbances after 1799, which prevented it from encountering the earth for 32 years, and it may again deviate from its path from the same cause.
It is now well ascertained that great showers of shooting stars occur also on the 12th of August, whose point of divergence is 423β Camelopardali, so that the earth’s atmosphere comes into contact with a zone of these small bodies twice in the year. By a systematic series of observations, MM. Benzenberg and Brand have clearly made out that the heights at which the falling stars appear and vanish vary from 16 miles to 140, and their velocities from 18 to 36 miles in a second, velocities so great as certainly to indicate a planetary revolution round the sun. As shooting stars are seen almost every night when the sky is clear, Sir John Lubbock has thought it probable that some of these bodies may have come so near, that the attraction of the earth has overcome that of the sun, and caused them to revolve as satellites round it. Should that be the case, they might shine by the reflected light of the sun, and suddenly cease to be visible on entering the earth’s shadow. The splitting of the falling stars like a rocket, and the trains of light, may be accounted for by supposing the stars to graze the surface of the shadow before being eclipsed; and the disappearance would be more or less rapid according to the breadth of the penumbra traversed. The calculations of M. Petit, Director of the Observatory of Toulouse, not only render probable the existence of small satellites, but tend to establish the identity of a body revolving round the earth in three hours and twenty minutes, at a distance of 5000 miles above its surface. It is evident that in this case the same satellite would be seen very often, and a very few would be sufficient to account for their nightly appearance. It is possible, however, that some shooting stars may belong to one class, and some to the other, since one group may be revolving about the sun, and another round the earth. In the case of a satellite shooting star, geometry furnishes the means of ascertaining its exact distance from the spectator, or from the centre of the earth, if the time and place of its disappearance be known with regard to the neighbouring stars. Since the falling stars are consumed in the atmosphere, their masses must be small, but it is possible that occasionally one may be large enough to arrive at the surface of the earth as an aërolite.
Diffusion of Matter through Space—Gravitation—Its Velocity—Simplicity of its Laws—Gravitation independent of the Magnitude and Distances of the Bodies—Not impeded by the intervention of any Substance—Its Intensity invariable—General Laws—Recapitulation and Conclusion.
The known quantity of matter bears a very small proportion to the immensity of space. Large as the bodies are, the distances which separate them are immeasurably greater; but, as design is manifest in every part of creation, it is probable that, if the various systems in the universe had been nearer to one another, their mutual disturbances would have been inconsistent with the harmony and stability of the whole. It is clear that space is not pervaded by atmospheric air of such density as that we breathe, since its resistance would long ere this have arrested the motion of the planets: it certainly is not a void, but replete with a medium possibly in itself electric or magnetic, but at all events capable of transmitting light, heat, magnetism, gravity, and probably influences of which we can form no idea.
Whatever the laws may be that obtain in the more distant regions of creation, we are assured that one alone regulates the motions, not only of our own system, but also of the binary systems of the fixed stars; and, as general laws form the ultimate object of philosophical research, we cannot conclude these remarks without considering the nature of gravitation—that extraordinary power whose effects we have been endeavouring to trace through some of their mazes. It was at one time imagined that the acceleration in the moon’s mean motion was occasioned by the successive transmission of the gravitating force. It has been proved that, in order to produce this effect, its velocity must be about fifty millions of times greater than that of light, which flies at the rate of 192,000 miles in a second. Its action, even at the distance of the sun, may therefore be regarded as instantaneous; yet, remote as the fixed stars are, the solar gravitation 425must have some influence on the nearest of them, as, for example, α Centauri, which is only 20,602 times the radius of the earth’s orbit from the sun, while La Place has computed that the solar gravitation extends a hundred millions of times farther than the semidiameter of the terrestrial orbit. Possibly the star dust in the Milky Way may be beyond, or on the verge of, that enormous limit; yet it is very unlikely that either the sun, or any of the stars which form the great cluster to which we belong, should be unconnected bodies.
The curves in which the celestial bodies move by the force of gravitation are only lines of the second order. The attraction of spheroids, according to any other law of force than that of gravitation, would be much more complicated; and, as it is easy to prove that matter might have been moved according to an infinite variety of laws, it may be concluded that gravitation must have been selected by Divine Wisdom out of an infinity of others, as being the most simple, and that which gives the greatest stability to the celestial motions.
It is a singular result of the simplicity of the laws of nature, which admit only of the observation and comparison of ratios, that the gravitation and theory of the motions of the celestial bodies are independent of their absolute magnitudes and distances. Consequently, if all the bodies of the solar system, their mutual distances, and their velocities, were to diminish proportionally, they would describe curves in all respects similar to those in which they now move; and the system might be successively reduced to the smallest sensible dimensions, and still exhibit the same appearances.
The action of the gravitating force is not impeded by the intervention even of the densest substances. If the attraction of the sun for the centre of the earth, and of the hemisphere diametrically opposite to him, were diminished by a difficulty in penetrating the interposed matter, the tides would be more obviously affected. Its attraction is the same also, whatever the substances of the celestial bodies may be; for, if the action of the sun upon the earth differed by a millionth part from his action upon the moon, the difference would occasion a periodical variation in the moon’s parallax, whose maximum would be the 1⁄15 of a second, and also a variation in her longitude amounting to several seconds—a supposition proved to be impossible by the agreement of 426theory with observation. Thus all matter is pervious to gravitation, and is equally attracted by it.
Gravitation is a feeble force, vastly inferior to electric action, chemical affinity, and cohesion; yet, as far as human knowledge extends, the intensity of gravitation has never varied within the limits of the solar system; nor does even analogy lead us to expect that it should: on the contrary, there is every reason to be assured that the great laws of the universe are immutable, like their Author. Nor can we suppose the structure of the globe alone to be exempt from the universal fiat of general laws, though ages may pass before the changes it has undergone, or that are now in progress, can be referred to existing causes with the same certainty with which the motions of the planets, and all their periodic and secular variations, are referable to the law of gravitation. The traces of extreme antiquity perpetually occurring to the geologist give that information, as to the origin of things, in vain looked for in the other parts of the universe. They date the beginning of time with regard to our system, since there is ground to believe that the formation of the earth was contemporaneous with that of the rest of the planets; but they show that creation is the work of Him with whom “a thousand years are as one day, and one day as a thousand years.”
In the work now brought to a conclusion, it has been necessary to select from the whole circle of the sciences a few of the most obvious of those proximate links which connect them together, and to pass over innumerable cases both of evident and occult alliance. Any one branch traced through its ramifications would alone have occupied a volume; it is hoped, nevertheless, that the view here given will suffice to show the extent to which a consideration of the reciprocal influence of even a few of these subjects may ultimately lead. It thus appears that the theory of dynamics, founded upon terrestrial phenomena, is indispensable for acquiring a knowledge of the revolutions of the celestial bodies and their reciprocal influences. The motions of the satellites are affected by the forms of their primaries, and the figures of the planets themselves depend upon their rotations. The symmetry of their internal structure proves the stability of these rotatory motions, and the immutability of the length of the day, which furnishes an invariable standard of time; and the actual size of the terrestrial spheroid affords the means of ascertaining 427the dimensions of the solar system, and provides an invariable foundation for a system of weights and measures. The mutual attraction of the celestial bodies disturbs the fluids at their surfaces, whence the theory of the tides and of the oscillations of the atmosphere. The density and elasticity of the air, varying with every alternation of temperature, lead to the consideration of barometrical changes, the measurement of heights, and capillary attraction; and the doctrine of sound, including the theory of music, is to be referred to the small undulations of the aërial medium. A knowledge of the action of matter upon light is requisite for tracing the curved path of its rays through the atmosphere, by which the true places of distant objects are determined, whether in the heavens or on the earth. By this we learn the nature and properties of the sunbeam, the mode of its propagation through the ethereal medium, or in the interior of material bodies, and the origin of colour. By the eclipses of Jupiter’s satellites the velocity of light is ascertained; and that velocity, in the aberration of the fixed stars, furnishes a direct proof of the real motion of the earth (N. 237). The effects of the invisible rays of the spectrum are immediately connected with chemical action; and heat, forming a part of the solar ray, so essential to animated and inanimated existence, is too important an agent in the economy of creation not to hold a principal place in the connexion of physical sciences; whence follows its distribution in the interior and over the surface of the globe, its power on the geological convulsions of our planet, its influence on the atmosphere and on climate, and its effects on vegetable and animal life, evinced in the localities of organized beings on the earth, in the waters, and in the air. The correlation between molecular and chemical action, light, heat, electricity, and magnetism, is continually becoming more perfect, and there is every reason to believe that these different modes of force, as well as gravity itself, will ultimately be found to merge in one great and universal power. Many more instances might be given in illustration of the immediate connexion of the physical sciences, most of which are united still more closely by the common bond of analysis, which is daily extending its empire, and will ultimately embrace almost every subject in nature in its formulæ.
These formulæ, emblematic of Omniscience, condense into a 428few symbols the immutable laws of the universe. This mighty instrument of human power itself originates in the primitive constitution of the human mind, and rests upon a few fundamental axioms, which have eternally existed in Him who implanted them in the breast of man when He created him after His own image.
Note 1, page 2. Diameter. A straight line passing through the centre, and terminated both ways by the sides or surface of a figure, such as of a circle or sphere. In fig. 1, q Q, N S, are diameters.
Note 2, p. 2. Mathematical and mechanical sciences. Mathematics teach the laws of number and quantity; mechanics treat of the equilibrium and motion of bodies.
Note 3, p. 2. Analysis is a series of reasoning conducted by signs or symbols of the quantities whose relations form the subject of inquiry.
Note 4, p. 3. Oscillations are movements to and fro, like the swinging of the pendulum of a clock, or waves in water. The tides are oscillations of the sea.
Note 5, p. 3. Gravitation. Gravity is the reciprocal attraction of matter on matter; gravitation is the difference between gravity and the centrifugal force induced by the velocity of rotation or revolution. Sensible gravity, or weight, is a particular instance of gravitation. It is the force which causes substances to fall to the surface of the earth, and which retains the celestial bodies in their orbits. Its intensity increases as the squares of the distance decrease.
Note 6, p. 4. Particles of matter are the indefinitely small or ultimate atoms into which matter is believed to be divisible. Their form is unknown; but, though too small to be visible, they must have magnitude.
Note 7, p. 4. A hollow sphere. A hollow ball, like a bomb-shell. A sphere is a ball or solid body, such, that all lines drawn from its centre to its surface are equal. They are called radii, and every line passing through the centre and terminated both ways by the surface is a diameter, which is consequently equal to twice the radius. In fig. 3, Q q or N S is a diameter, and C Q, C N are radii. A great circle of the sphere has the same centre with the sphere as the circles Q E q d and Q N q S. The circle A B is a lesser circle of the sphere.
Note 8, p. 4. Concentric hollow spheres. Shells, or hollow spheres, having the same centre, like the coats of an onion.
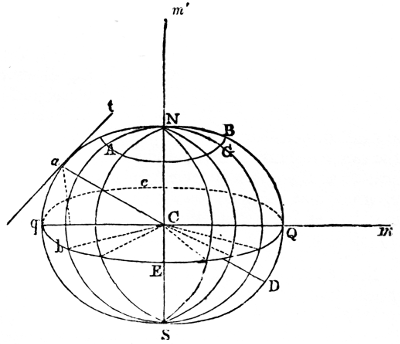
Fig. 1.
Note 9, p. 4. Spheroid. A solid body, which sometimes has the shape of an orange, as in fig. 1; 430it is then called an oblate spheroid, because it is flattened at the poles N and S. Such is the form of the earth and planets. When, on the contrary, it is drawn out at the poles like an egg, as in fig. 2, it is called a prolate spheroid. It is evident that in both these solids the radii C q, C a, C N, &c., are generally unequal; whereas in the sphere they are all equal.
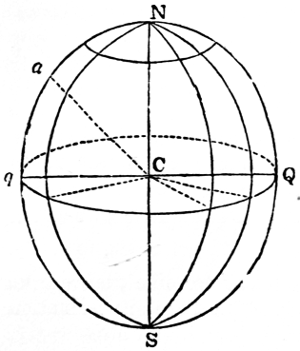
Fig. 2.
Note 10, p. 4. Centre of gravity. A point in every body, which if supported, the body will remain at rest in whatever position it may be placed. About that point all the parts exactly balance one another. The celestial bodies attract each other as if each were condensed into a single particle situate in the centre of gravity, or the particle situate in the centre of gravity of each may be regarded as possessing the resultant power of the innumerable oblique forces which constitute the whole attraction of the body.
Note 11, pp. 4, 6. Poles and equator. Let fig. 1 or 3 represent the earth, C its centre, N C S the axis of rotation, or the imaginary line about which it performs its daily revolution. Then N and S are the north and south poles, and the great circle q E Q, which divides the earth into two equal parts, is the equator. The earth is flattened at the poles, fig. 1, the equatorial diameter, q Q, exceeding the polar diameter, N S, by about 261⁄2 miles. Lesser circles, A B G, which are parallel to the equator, are circles or parallels of latitude, which is estimated in degrees, minutes, and seconds, north and south of the equator, every place in the same parallel having the same latitude. Greenwich is in the parallel of 51° 28ʹ 40ʺ. Thus terrestrial latitude is the angular distance between the direction of a plumb-line at any place and the plane of the equator. Lines such as N Q S, N G E S, fig. 3, are called meridians; all the places in any one of these lines have noon at the same instant. The meridian of Greenwich has been chosen by the British as the origin of terrestrial longitude, which is estimated in degrees, minutes, and seconds, east and west of that line. If N G E S be the meridian of Greenwich, the position of any place, B, is determined, when its latitude, Q C B, and its longitude, E C Q, are known.
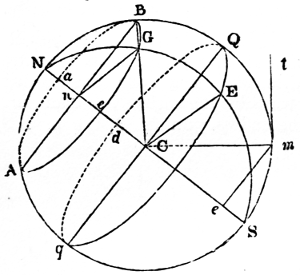
Fig. 3.
Note 12, p. 4. Mean quantities are such as are intermediate between others that are greater and less. The mean of any number of unequal quantities is equal to their sum divided by their number. For instance, the mean between two unequal quantities is equal to half their sum.
431Note 13, p. 4. A certain mean latitude. The attraction of a sphere on an external body is the same as if its mass were collected into one heavy particle in its centre of gravity, and the intensity of its attraction diminishes as the square of its distance from the external body increases. But the attraction of a spheroid, fig. 1, on an external body at m in the plane of its equator, E Q, is greater, and its attraction on the same body when at mʹ in the axis N S less, than if it were a sphere. Therefore, in both cases, the force deviates from the exact law of gravity. This deviation arises from the protuberant matter at the equator; and, as it diminishes towards the poles, so does the attractive force of the spheroid. But there is one mean latitude, where the attraction of a spheroid is the same as if it were a sphere. It is a part of the spheroid intermediate between the equator and the pole. In that latitude the square of the sine is equal to 1⁄3 of the equatorial radius.
Note 14, p. 4. Mean distance. The mean distance of a planet from the centre of the sun, or of a satellite from the centre of its planet, is equal to half the sum of its greatest and least distances, and, consequently, is equal to half the major axis of its orbit. For example, let P Q A D, fig. 6, be the orbit or path of the moon or of a planet; then P A is the major axis, C the centre, and C S is equal to C F. Now, since the earth or the sun is supposed to be in the point S according as P D A Q is regarded as the orbit of the moon or that of a planet, S A, S P are the greatest and least distances. But half the sum of S A and S P is equal to half of A P, the major axis of the orbit. When the body is at Q or D, it is at its mean distance from S, for S Q, S D, are each equal to C P, half the major axis by the nature of the curve.
Note 15, p. 4. Mean radius of the earth. The distance from the centre to the surface of the earth, regarded as a sphere. It is intermediate between the distances of the centre of the earth from the pole and from the equator.
Note 16, p. 5. Ratio. The relation which one quantity bears to another.
Note 17, p. 5. Square of moon’s distance. In order to avoid large numbers, the mean radius of the earth is taken for unity: then the mean distance of the moon is expressed by 60; and the square of that number is 3600, or 60 times 60.
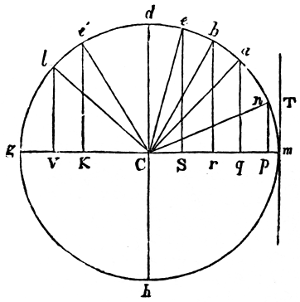
Fig. 4
Note 18, p. 5. Centrifugal force. The force with which a revolving body tends to fly from the centre of motion: a sling tends to fly from the hand in consequence of the centrifugal force. A tangent is a straight line touching a curved line in one point without cutting it, as m T, fig. 4. The direction of the centrifugal force is in the tangent to the curved line or path in which the body revolves, and its intensity increases with the angular swing of the body, and with its distance from the 432centre of motion. As the orbit of the moon does not differ much from a circle, let it be represented by m d g h, fig. 4, the earth being in C. The centrifugal force arising from the velocity of the moon in her orbit balances the attraction of the earth. By their joint action, the moon moves through the arc m n during the time that she would fly off in the tangent m T by the action of the centrifugal force alone, or fall through m p by the earth’s attraction alone. T n, the deflection from the tangent, is parallel and equal to m p, the versed sine of the arc m n, supposed to be moved over by the moon in a second, and therefore so very small that it may be regarded as a straight line. T n, or m p, is the space the moon would fall through in the first second of her descent to the earth, were she not retained in her orbit by her centrifugal force.
Note 19, p. 5. Action and reaction. When motion is communicated by collision or pressure, the action of the body which strikes is returned with equal force by the body which receives the blow. The pressure of a hand on a table is resisted with an equal and contrary force. This necessarily follows from the impenetrability of matter, a property by which no two particles of matter can occupy the same identical portion of space at the same time. When motion is communicated without apparent contact, as in gravitation, attraction, and repulsion, the quantity of motion gained by the one body is exactly equal to that lost by the other, but in a contrary direction; a circumstance known by experience only.
Note 20, p. 5. Projected. A body is projected when it is thrown: a ball fired from a gun is projected; it is therefore called a projectile. But the word has also another meaning. A line, surface, or solid body, is said to be projected upon a plane, when parallel straight lines are drawn from every point of it to the plane. The figure so traced upon a plane is a projection. The projection of a terrestrial object is therefore its daylight shadow, since the sun’s rays are sensibly parallel.
Note 21, p. 5. Space. The boundless region which contains all creation.
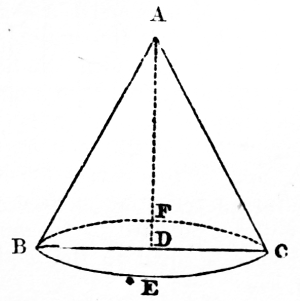
Fig. 5.
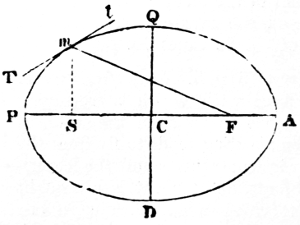
Fig. 6.
Note 22, pp. 5, 11. Conic sections. Lines formed by any plane cutting a cone. A cone is a solid figure, like a sugar-loaf, fig. 5, of which A is the apex, A D the axis, and the plane B E C F the base. The axis may or may not be perpendicular to the base, and the base may be a circle, or 433any other curved line. When the axis is perpendicular to the base, the solid is a right cone. If a right cone with a circular base be cut at right angles to the base by a plane passing through the apex, the section will be a triangle. If the cone be cut through both sides by a plane parallel to the base, the section will be a circle. If the cone be cut slanting quite through both sides, the section will be an ellipse, fig. 6. If the cone be cut parallel to one of the sloping sides as A B, the section will be a parabola, fig. 7. And if the plane cut only one side of the cone, and be not parallel to the other, the section will be a hyperbola, fig. 8. Thus there are five conic sections.
Fig. 7.
Fig. 8.
Note 23, p. 5. Inverse square of distance. The attraction of one body for another at the distance of two miles is four times less than at the distance of one mile; at three miles, it is nine times less than at one; at four miles, it is sixteen times less, and so on. That is, the gravitating force decreases in intensity as the squares of the distance increase.
Note 24, p. 5. Ellipse. One of the conic sections, fig. 6. An ellipse may be drawn by fixing the ends of a string to two points, S and F, in a sheet of paper, and then carrying the point of a pencil round in the loop of the string kept stretched, the length of the string being greater than the distance between the two points. The points S and F are called the foci, C the centre, S C or C F the excentricity, A P the major axis, Q D the minor axis, and P S the focal distance. It is evident that, the less the excentricity C S, the nearer does the ellipse approach to a circle; and from the construction it is clear that the length of the string S m F is equal to the major axis P A. If T t be a tangent to the ellipse at m, then the angle T m S is equal to the angle t m F; and, as this is true for every point in the ellipse, it follows that, in an elliptical reflecting surface, rays of light or sound coming from one focus S will be reflected by the surface to the other focus F, since the angle of incidence is equal to the angle of reflection by the theories of light and sound.
Note 25, p. 5. Periodic time. The time in which a planet or comet performs a revolution round the sun, or a satellite about its planet.
434Note 26, p. 5. Kepler discovered three laws in the planetary motions by which the principle of gravitation is established:—1st law, That the radii vectores of the planets and comets describe areas proportional to the time.—Let fig. 9 be the orbit of a planet; then, supposing the spaces or areas P S p, p S a, a S b, &c., equal to one another, the radius vector S P, which is the line joining the centres of the sun and planet, passes over these equal spaces in equal times; that is, if the line S P passes to S p in one day, it will come to S a in two days, to S b in three days, and so on. 2nd law, That the orbits or paths of the planets and comets are conic sections, having the sun in one of their foci. The orbits of the planets and satellites are curves like fig. 6 or 9, called ellipses, having the sun in the focus S. Several comets are known to move in ellipses; but the greater part seem to move in parabolas, fig. 7, having the sun in S, though it is probable that they really move in very long flat ellipses; others appear to move in hyperbolas, like fig. 8. The third law is, that the squares of the periodic times of the planets are proportional to the cubes of their mean distances from the sun. The square of a number is that number multiplied by itself, and the cube of a number is that number twice multiplied by itself. For example, the squares of the numbers 2, 3, 4, &c., are 4, 9, 16, &c., but their cubes are 8, 27, 64, &c. Then the squares of the numbers representing the periodic times of two planets are to one another as the cubes of the numbers representing their mean distances from the sun. So that, three of these quantities being known, the other may be found by the rule of three. The mean distances are measured in miles or terrestrial radii, and the periodic times are estimated in years, days, and parts of a day. Kepler’s laws extend to the satellites.
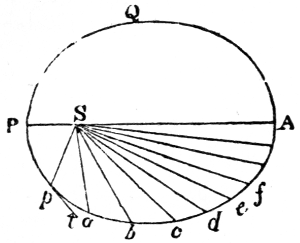
Fig. 9.
Note 27, p. 5. Mass. The quantity of matter in a given bulk. It is proportional to the density and volume or bulk conjointly.
Note 28, p. 5. Gravitation proportional to mass. But for the resistance of the air, all bodies would fall to the ground in equal times. In fact, a hundred equal particles of matter at equal distances from the surface of the earth would fall to the ground in parallel straight lines with equal rapidity, and no change whatever would take place in the circumstances of their descent, if 99 of them were united in one solid mass; for the solid mass and the single particle would touch the ground at the same instant, were it not for the resistance of the air.
Note 29, p. 5. Primary signifies, in astronomy, the planet about which a satellite revolves. The earth is primary to the moon.
Note 30, p. 6. Rotation. Motion round an axis, real or imaginary.
Note 31, p. 7. Compression of a spheroid. The flattening at the poles. It is equal to the difference between the greatest and least diameters, divided by the greatest, these quantities being expressed in some standard measure, as miles.
435Note 32, p. 7. Satellites. Small bodies revolving about some of the planets. The moon is a satellite to the earth.
Note 33, p. 7. Nutation. A nodding motion in the earth’s axis while in rotation, similar to that observed in the spinning of a top. It is produced by the attraction of the sun and moon on the protuberant matter at the terrestrial equator.
Note 34, p. 7. Axis of rotation. The line, real or imaginary, about which a body revolves. The axis of the earth’s rotation is that diameter, or imaginary line, passing through the centre and both poles. Fig. 1 being the earth, N S is the axis of rotation.
Note 35, p. 7. Nutation of lunar orbit. The action of the bulging matter at the earth’s equator on the moon occasions a variation in the inclination of the lunar orbit to the plane of the ecliptic. Suppose the plane N p n, fig. 13, to be the orbit of the moon, and N m n the plane of the ecliptic, the earth’s action on the moon causes the angle p N m to become less or greater than its mean state. The nutation in the lunar orbit is the reaction of the nutation in the earth’s axis.
Note 36, p. 7. Translated. Carried forward in space.
Note 37, p. 7. Force proportional to velocity. Since a force is measured by its effect, the motions of the bodies of the solar system among themselves would be the same whether the system be at rest or not. The real motion of a person walking the deck of a ship at sea is compounded of his own motion and that of the ship, yet each takes place independently of the other. We walk about as if the earth were at rest, though it has the double motion of rotation on its axis and revolution round the sun.
Note 38, p. 8. Tangent. A straight line which touches a curved line in one point without cutting it. In fig. 4, m T is tangent to the curve in the point m. In a circle the tangent is at right angles to the radius, C m.
Note 39, p. 8. Motion in an elliptical orbit. A planet m, fig. 6, moves round the sun at S in an ellipse P D A Q, in consequence of two forces, one urging it in the direction of the tangent m T, and another pulling it towards the sun in the direction m S. Its velocity, which is greatest at P, decreases throughout the arc to P D A to A, where it is least, and increases continually as it moves along the arc A Q P till it comes to P again. The whole force producing the elliptical motion varies inversely as the square of the distance. See note 23.
Note 40, p. 8. Radii vectores. Imaginary lines adjoining the centre of the sun and the centre of a planet or comet, or the centres of a planet and its satellite. In the circle, the radii are all equal; but in an ellipse, fig. 6, the radius vector S A is greater, and S P less than all the others. The radii vectores S Q, S D, are equal to C A or C P, half the major axis P A, and consequently equal to the mean distance. A planet is at its mean distance from the sun when in the points Q and D.
Note 41, p. 8. Equal areas in equal times. See Kepler’s 1st law, in note 26, p. 5.
Note 42, p. 8. Major axis. The line P A, fig. 6 or 10.
436Note 43, p. 8. If the planet described a circle, &c. The motion of a planet about the sun, in a circle A B P, fig. 10, whose radius C A is equal to the planet’s mean distance from him, would be equable, that is, its velocity, or speed, would always be the same. Whereas, if it moved in the ellipse A Q P, its speed would be continually varying, by note 39; but its motion is such, that the time elapsing between its departure from P and its return to that point again would be the same whether it moved in the circle or in the ellipse; for these curves coincide in the points P and A.
Note 44, p. 8. True motion. The motion of a body in its real orbit P D A Q, fig. 10.
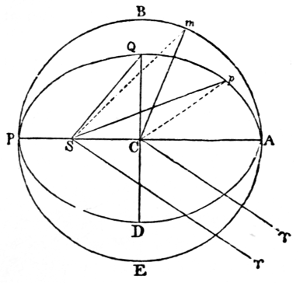
Fig. 10.
Note 45, p. 9. Mean motion. Equable motion in a circle P E A B, fig. 10, at the mean distance C P or C m, in the time that the body would accomplish a revolution in its elliptical orbit P D A Q.
Note 46, p. 9. The equinox. Fig. 11 represents the celestial sphere, and C its centre, where the earth is supposed to be. q ♈ Q ♎ is the equinoctial or great circle, traced in the starry heavens by an imaginary extension of the plane of the terrestrial equator, and E ♈ e ♎ is the ecliptic, or apparent path of the sun round the earth. ♈ ♎, the intersection of these two planes, is the line of the equinoxes; ♈ is the vernal equinox, and ♎ the autumnal. When the sun is in these points, the days and nights are equal. They are distant from one another by a semicircle, or two right angles. The points E and e are the solstices, where the sun is at his greatest distance from the equinoctial. The equinoctial is everywhere ninety degrees distant from its poles N and S, which are two points diametrically opposite to one another, where the axis of the earth’s rotation, if prolonged, would meet the heavens. The northern celestial pole N is within 1° 24ʹ of the pole star. As the latitude of any place on the surface of the earth is equal to the height of the pole above the horizon, it is easily determined by observation. The ecliptic E ♈ e ♎ is also everywhere ninety degrees distant from its poles P and p. The angle P C N, between the poles P and N of the equinoctial and ecliptic, is equal to the angle e C Q, called the obliquity of the ecliptic.
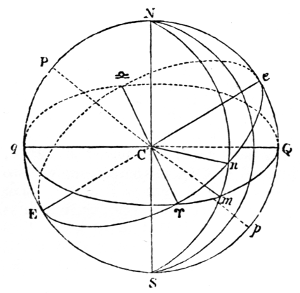
Fig. 11.
437Note 47, p. 9. Longitude. The vernal equinox, ♈, fig. 11, is the zero point in the heavens whence celestial longitudes, or the angular motions of the celestial bodies, are estimated from west to east, the direction in which they all revolve. The vernal equinox is generally called the first point of Aries, though these two points have not coincided since the early ages of astronomy, about 2233 years ago, on account of a motion in the equinoctial points, to be explained hereafter. If S ♈, fig. 10, be the line of the equinoxes, and ♈ the vernal equinox, the true longitude of a planet p is the angle ♈ S p, and its mean longitude is the angle ♈ C m, the sun being in S. Celestial longitude is the angular distance of a heavenly body from the vernal equinox; whereas terrestrial longitude is the angular distance of a place on the surface of the earth from a meridian arbitrarily chosen, as that of Greenwich.
Note 48, pp. 9, 58. Equation of the centre. The difference between ♈ C m and ♈ S p, fig. 10; that is, the difference between the true and mean longitudes of a planet or satellite. The true and mean places only coincide in the points P and A; in every other point of the orbit, the true place is either before or behind the mean place. In moving from A through the arc A Q P, the true place p is behind the mean place m; and through the arc P D A the true place is before the mean place. At its maximum, the equation of the centre measures C S, the excentricity of the orbit, since it is the difference between the motion of a body in an ellipse and in a circle whose diameter A P is the major axis of the ellipse.
Note 49, p. 9. Apsides. The points P and A, fig. 10, at the extremities of the major axis of an orbit. P is commonly called the perihelion, a Greek term signifying round the sun; and the point A is called the aphelion, a Greek term signifying at a distance from the sun.
Note 50, p. 9. Ninety degrees. A circle is divided into 360 equal parts, or degrees; each degree into 60 equal parts, called minutes; and each minute into 60 equal parts, called seconds. It is usual to write these quantities thus, 15° 16ʹ 10ʺ, which means fifteen degrees, sixteen minutes, and ten seconds. It is clear that an arc m n, fig. 4, measures the angle m C n; hence we may say, an arc of so many degrees, or an angle of so many degrees; for, if there be ten degrees in the angle m C n, there will be ten degrees in the arc m n. It is evident that there are 90° in a right angle, m C d, or quadrant, since it is the fourth part of 360°.
Note 51, p. 9. Quadratures. A celestial body is said to be in quadrature when it is 90 degrees distant from the sun. For example, in fig. 14, if d be the sun, S the earth, and p the moon, then the moon is said to be in quadrature when she is in either of the points Q or D, because the angles Q S d and D S d, which measure her apparent distance from the sun, are right angles.
Note 52, p. 9. Excentricity. Deviation from circular form. In fig. 6, C S is the excentricity of the orbit P Q A D. The less C S, the more nearly does the orbit or ellipse approach the circular form; and, when C S is zero, the ellipse becomes a circle.
Note 53, p. 9. Inclination of an orbit. Let S, fig. 12, be the centre of the sun, P N A n the orbit of a planet moving from west to east in the 438direction N p. Let E N m e n be the shadow or projection of the orbit on the plane of the ecliptic, then N S n is the intersection of these two planes, for the orbit rises above the plane of the ecliptic towards N p, and sinks below it at N P. The angle p N m, which these two planes make with one another, is the inclination of the orbit P N p A to the plane of the ecliptic.
Note 54, p. 9. Latitude of a planet. The angle p S m, fig. 12, or the height of the planet p above the ecliptic E N m. In this case the latitude is north. Thus, celestial latitude is the angular distance of a celestial body from the plane of the ecliptic, whereas terrestrial latitude is the angular distance of a place on the surface of the earth from the equator.
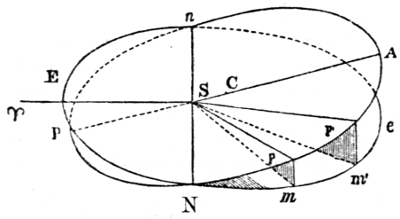
Fig. 12.
Note 55, p. 9. Nodes. The two points N and n, fig. 12, in which the orbit N A n P of a planet or comet intersects the plane of the ecliptic e N E n. The part N A n of the orbit lies above the plane of the ecliptic, and the part n P N below it. The ascending node N is the point through which the body passes in rising above the plane of the ecliptic, and the descending node n is the point in which the body sinks below it. The nodes of a satellite’s orbit are the points in which it intersects the plane of the orbit of the planet.
Note 56, p. 10. Distance from the sun. S p in fig. 12. If ♈ be the vernal equinox, then ♈ S p is the longitude of the planet p, m S p is its latitude, and S p its distance from the sun. When these three quantities are known, the place of the planet p is determined in space.
Note 57, pp. 10, 59. Elements of an orbit. Of these there are seven. Let P N A n, fig. 12, be the elliptical orbit of a planet, C its centre, S the sun in one of the foci, ♈ the point of Aries, and E N e n the plane of the ecliptic. The elements are—the major axis A P; the excentricity C S; the periodic time, that is, the time of a complete revolution of the body in its orbit; and the fourth is the longitude of the body at any given instant—for example, that at which it passes through the perihelion P, the point of its orbit nearest to the sun. That instant is assumed as the origin of time, whence all preceding and succeeding periods are estimated. These four quantities are sufficient to determine the form of the orbit, and the motion of the body in it. Three other elements are requisite for determining the position of the orbit in space. These are, the angle ♈ S P, the longitude of the perihelion; the angle A N e, which is the inclination of the orbit to the plane of the ecliptic; and, lastly, the angle ♈ S N, the longitude of N the ascending node.
Note 58, p. 10. Whose planes, &c. The planes of the orbits, as P N A n, fig. 12, in which the planets move, are inclined or make small angles e N A with the plane of the ecliptic E N e n, and cut it in straight lines, N S n passing through S, the centre of the sun.
439Note 59, p. 11. Momentum. Force measured by the weight of a body and its speed, or simple velocity, conjointly. The primitive momentum of the planets is, therefore, the quantity of motion which was impressed upon them when they were first thrown into space.
Note 60, p. 11. Unstable equilibrium. A body is said to be in equilibrium when it is so balanced as to remain at rest. But there are two kinds of equilibrium, stable and unstable. If a body balanced in stable equilibrium be slightly disturbed, it will endeavour to return to rest by a number of movements to and fro, which will continually decrease till they cease altogether, and then the body will be restored to its original state of repose. But, if the equilibrium be unstable, these movements to and fro, or oscillations, will become greater and greater till the equilibrium is destroyed.
Note 61, p. 14. Retrograde. Going backwards, as from east to west, contrary to the motion of the planets.
Note 62, p. 14. Parallel directions. Such as never meet, though prolonged ever so far.
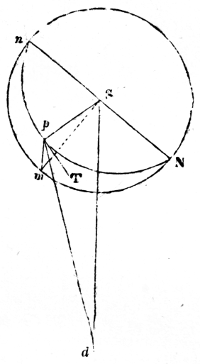
Fig. 13.
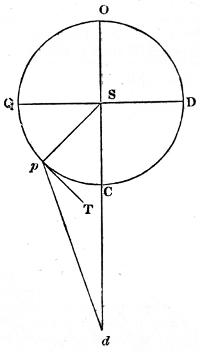
Fig. 14.
Note 63, pp. 14, 16. The whole force, &c. Let S, fig. 13, be the sun, N m n the plane of the ecliptic, p the disturbed planet moving in its orbit n p N, and d the disturbing planet. Now, d attracts the sun and the planet p with different intensities in the directions d S, d p: the difference only of these forces disturbs the motion of p; it is therefore called the disturbing force. But this whole disturbing force may be regarded as equivalent to three forces, acting in the directions p S, p T, and p m. The force acting in the radius vector p S, joining the centres of the sun and planet, is called the radial force. It sometimes draws the disturbed planet p from the sun, and sometimes brings it nearer to him. The force which acts in 440the direction of the tangent p T is called the tangential force. It disturbs the motion of p in longitude, that is, it accelerates its motion in some parts of its orbit and retards it in others, so that the radius vector S p does not move over equal areas in equal times. (See note 26.) For example, in the position of the bodies in fig. 14, it is evident that, in consequence of the attraction of d, the planet p will have its motion accelerated from Q to C, retarded from C to D, again accelerated from D to O, and lastly retarded from O to Q. The disturbing body is here supposed to be at rest, and the orbit circular; but, as both bodies are perpetually moving with different velocities in ellipses, the perturbations or changes in the motions of p are very numerous. Lastly, that part of the disturbing force which acts in the direction of a line p m, fig. 13, at right angles to the plane of the orbit N p n, may be called the perpendicular force. It sometimes causes the body to approach nearer, and sometimes to recede farther from, the plane of the ecliptic N m n, than it would otherwise do. The action of the disturbing forces is admirably explained in a work on gravitation, by Mr. Airy, the Astronomer Royal.
Note 64, pp. 16, 74. Perihelion. Fig. 10, P, the point of an orbit nearest the sun.
Note 65, p. 16. Aphelion. Fig. 10, A, the point of an orbit farthest from the sun.
Note 66, pp. 16, 17. In fig. 15 the central force is greater than the exact law of gravity; therefore the curvature P p a is greater than P p A the real ellipse; hence the planet p comes to the point a, called the aphelion, sooner than if it moved in the orbit P p A, which makes the line P S A advance to a. In fig. 16, on the contrary, the curvature P p a is less than in the true ellipse, so that the planet p must move through more than the arc P p A, or 180°, before it comes to the aphelion a, which causes the greater axis P S A to recede to a.

Fig. 15.
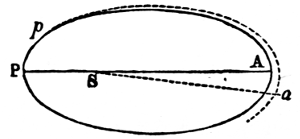
Fig. 16.
Note 67, pp. 16, 17. Motion of apsides. Let P S A, fig. 17, be the position of the elliptical orbit of a planet, at any time; then, by the action of the disturbing forces, it successively takes the position Pʹ S Aʹ, Pʺ S Aʺ, &c., till by this direct motion it has accomplished a revolution, and then it begins again; so that the motion is perpetual.
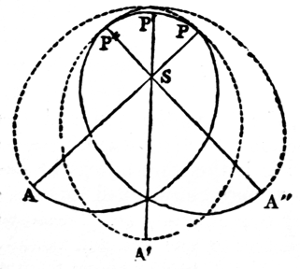
Fig. 17.
Note 68, p. 17. Sidereal revolution. The consecutive return of an object to the same star.
441Note 69, p. 17. Tropical revolution. The consecutive return of an object to the same tropic or equinox.
Note 70, p. 17. The orbit only bulges, &c. In fig. 18 the effect of the variation in the excentricity is shown where P p A is the elliptical orbit at any given instant; after a time it will take the form P pʹ A, in consequence of the decrease in the excentricity C S; then the forms P pʺ A, P pʹʹʹ A, &c., consecutively from the same cause; and, as the major axis P A always retains the same length, the orbit approaches more and more nearly to the circular form. But, after this has gone on for some thousands of years, the orbit contracts again, and becomes more and more elliptical.
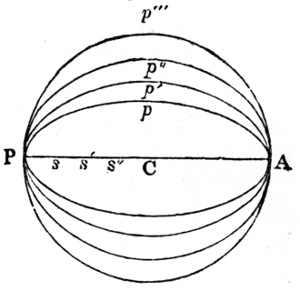
Fig. 18.
Note 71, pp. 18, 19. The ecliptic is the apparent path of the sun in the heavens. See note 46.
Note 72, p. 18. This force tends to pull, &c. The force in question, acting in the direction p m, fig. 13, pulls the planet p towards the plane N m n, or pushes it farther above it, giving the planet a tendency to move in an orbit above or below its undisturbed orbit N p n, which alters the angle p N m, and makes the node N and the line of nodes N n change their positions.
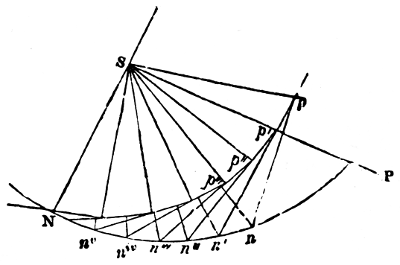
Fig. 19.
Note 73, p. 18. Motion of the nodes. Let S, fig. 19, be the sun; S N n the plane of the ecliptic; P the disturbing body; and p a planet moving in its orbit p n, of which p n is so small a part that it is represented as a straight line. The plane S n p of this orbit cuts the plane of the ecliptic in the straight line S n. Suppose the disturbing force begins to act on p, so as to draw the planet into the arc p pʹ; then, instead of moving in the orbit p n, it will tend to move in the orbit p pʹ nʹ, whose plane cuts the ecliptic in the straight line S nʹ. If the disturbing force acts again upon the body when at pʹ, so as to draw it into the arc pʹ pʺ, the planet will now 442tend to move in the orbit pʹ pʺ nʺ, whose plane cuts the ecliptic in the straight line S nʺ. The action of the disturbing force on the planet when at pʺ will bring the node to nʹʹʹ, and so on. In this manner the node goes backwards through the successive points n, nʹ, nʺ, nʹʹʹ, &c., and the line of nodes S n has a perpetual retrograde motion about S, the centre of the sun. The disturbing force has been represented as acting at intervals for the sake of illustration: in nature it is continuous, so that the motion of the node is continuous also; though it is sometimes rapid and sometimes slow, now retrograde and now direct; but, on the whole, the motion is slowly retrograde.
Note 74, p. 18. When the disturbing planet is anywhere in the line S N, fig. 19, or in its prolongation, it is in the same plane with the disturbed planet; and, however much it may affect its motions in that plane, it can have no tendency to draw it out of it. But when the disturbing planet is in P, at right angles to the line S N, and not in the plane of the orbit, it has a powerful effect on the motion of the nodes: between these two positions there is great variety of action.
Note 75, p. 19. The changes in the inclination are extremely minute when compared with the motion of the node, as evidently appears from fig. 19, where the angles n p nʹ, nʹ pʹ nʺ, &c., are much smaller than the corresponding angles n S nʹ, S nʺ, &c.
Note 76, p. 20. Sines and cosines. Figure 4 is a circle; n p is the sine, and C p is the cosine of an arc m n. Suppose the radius C m to begin to revolve at m, in the direction m n a; then at the point m the sine is zero, and the cosine is equal to the radius C m. As the line C m revolves and takes the successive positions C n, C a, C b, &c., the sines n p, a q, b r, &c., of the arcs m n, m a, m h, &c., increase, while the corresponding cosines C p, C q, C r, &c., decrease; and when the revolving radius takes the position C d, at right angles to the diameter g m, the sine becomes equal to the radius C d, and the cosine is zero. After passing the point d, the contrary happens; for the sines e K, l V, &c., diminish, and the cosines C K, C V, &c., go on increasing, till at g the sine is zero, and the cosine is equal to the radius C g. The same alternation takes place through the remaining parts g h, h m, of the circle, so that a sine or cosine never can exceed the radius. As the rotation of the earth is invariable, each point of its surface passes through a complete circle, or 360 degrees, in twenty-four hours, at a rate of 15 degrees in an hour. Time, therefore, becomes a measure of angular motion, and vice versâ, the arcs of a circle a measure of time, since these two quantities vary simultaneously and equably; and, as the sines and cosines of the arcs are expressed in terms of the time, they vary with it. Therefore, however long the time may be, and how often soever the radius may revolve round the circle, the sines and cosines never can exceed the radius; and, as the radius is assumed to be equal to unity, their values oscillate between unity and zero.
Note 77, p. 20. The small excentricities and inclinations of the planetary orbits, and the revolutions of all the bodies in the same direction, were proved by Euler, La Grange, and La Place, to be conditions necessary for the stability of the solar system. Subsequently, however, the periodicity of the terms of the series expressing the perturbations was 443supposed to be sufficient alone, but M. Poisson has shown that to be a mistake; that these three conditions are requisite for the necessary convergence of the series, and that therefore the stability of the system depends on them conjointly with the periodicity of the sines and cosines of each term. The author is aware that this note can only be intelligible to the analyst, but she is desirous of correcting an error, and the more so as the conditions of stability afford one of the most striking instances of design in the original construction of our system, and of the foresight and supreme wisdom of the Divine Architect.
Note 78, p. 22. Resisting medium. A fluid which resists the motions of bodies, such as atmospheric air, or the highly elastic fluid called ether, with which space is filled.
Note 79, p. 23. Obliquity of the ecliptic. The angle e ♈ q, fig. 11, between the plane of the terrestrial equator q ♈ Q, and the plane of the ecliptic E ♈ e. The obliquity is variable.
Note 80, p. 23. Invariable plane. In the earth the equator is the invariable plane which nearly maintains a parallel position with regard to itself while revolving about the sun, as in fig. 20, where E Q represents it. The two hemispheres balance one another on each side of this plane, and would still do so if all the particles of which they consist were moveable among themselves, provided the earth were not disturbed by the action of the sun and moon, which alters the parallelism of the equator by the small variation called nutation, to be explained hereafter.
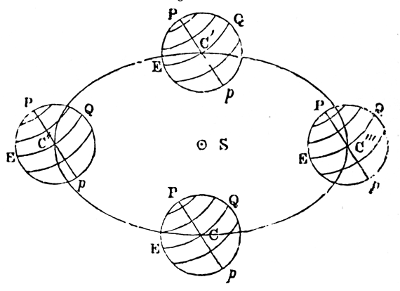
Fig. 20.
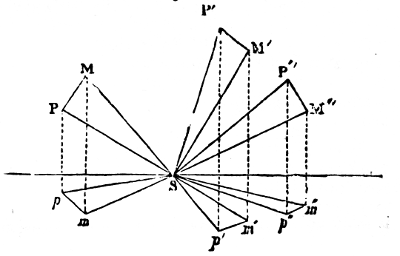
Fig. 21.
Note 81, p. 24. If each particle, &c. Let P, Pʹ, Pʺ, &c., fig. 21, be planets moving in their orbits about the centre of gravity of the system. Let P S M, Pʹ S Mʹ, &c., be portions of these orbits moved over by the radii vectores S P, S Pʹ, &c., in a given time, and let p S m, pʹ S mʹ, &c., be their shadows or projections on the invariable plane. Then, if the numbers which represent 444the masses of the planets P, Pʹ, &c., be respectively multiplied by the numbers representing the areas or spaces p S m, pʹ S mʹ, &c., the sum of the whole will be greater for the invariable plane than it would be for any plane that could pass through S, the centre of gravity of the system.
Note 82, p. 24. The centre of gravity of the solar system lies within the body of the sun, because his mass is much greater than the masses of all the planets and satellites added together.
Note 83, pp. 25, 36. Conjunction. A planet is said to be in conjunction when it has the same longitude with the sun, and in opposition when its longitude differs from that of the sun by 180 degrees. Thus two bodies are said to be in conjunction when they are seen exactly in the same part of the heavens, and in opposition when diametrically opposite to one another. Mercury and Venus, which are nearer to the sun than the earth, are called inferior planets; while all the others, being farther from the sun than the earth, are said to be superior planets. Suppose the earth to be at E, fig. 24; then a superior planet will be in conjunction with the sun at C, and in opposition to him when at O. Again, suppose the earth to be in O, then an inferior planet will be in conjunction when at E, and in opposition when at F.
Note 84, p. 26. The periodic inequalities are computed for a given time; and consequently for a given form and position of the orbits of the disturbed and disturbing bodies. Although the elements of the orbits vary so slowly that no sensible effect is produced on inequalities of a short period, yet, in the course of time, the secular variations of the elements change the forms and relative positions of the orbits so much, that Jupiter and Saturn, which would have come to the same relative positions with regard to the sun and to one another after 850 years, do not arrive at the same relative positions till after 918 years.
Note 85, p. 26. Configuration. The relative position of the planets with regard to one another, to the sun, and to the plane of the ecliptic.
Note 86, p. 27. In the same manner that the excentricity of an elliptical orbit may be increased or diminished by the action of the disturbing forces, so a circular orbit may acquire less or more ellipticity from the same cause. It is thus that the forms of the orbits of the first and second satellites of Jupiter oscillate between circles and ellipses differing very little from circles.
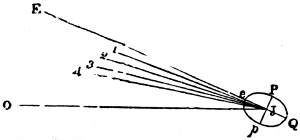
Fig. 22.
Note 87, p. 28. The plane of Jupiter’s equator is the imaginary plane passing through his centre at right angles to his axis of rotation, and corresponds to the plane q E Q e, in fig. 1. The satellites move very nearly in the plane of Jupiter’s equator; for, if J be Jupiter, fig. 22, P p his axis of rotation, e Q his equatorial diameter, which is 6000 miles longer than P p, and if J O and J E be the planes of his orbit 445and equator seen edgewise, then the orbits of his four satellites seen edgewise will have the positions J1, J2, J3, J4. These are extremely near to one another, for the angle E J O is only 3° 5ʹ 30ʺ.
Note 88, p. 28. In consequence of the satellites moving so nearly in the plane of Jupiter’s equator, when seen from the earth, they appear to be always very nearly in a straight line, however much they may change their positions with regard to one another and to their primary. For example, on the evenings of the 3rd, 4th, 5th, and 6th of January, 1835, the satellites had the configurations given in fig. 23, where O is Jupiter, and 1, 2, 3, 4, are the first, second, third, and fourth satellites. The satellite is supposed to be moving in a direction from the figure towards the point. On the sixth evening the second satellite was seen on the disc of the planet.

Fig. 23.
Note 89, p. 28. Angular motion or velocity is the swiftness with which a body revolves—a sling, for example; or the speed with which the surface of the earth performs its daily rotation about its axis.
Note 90, p. 29. Displacement of Jupiter’s orbit. The action of the planets occasions secular variations in the position of Jupiter’s orbit J O, fig. 22, without affecting the plane of his equator J E. Again, the sun and satellites themselves, by attracting the protuberant matter at Jupiter’s equator, change the position of the plane J E without affecting J O. Both of these cause perturbations in the motions of the satellites.
Note 91, p. 29. Precession, with regard to Jupiter, is a retrograde motion of the point where the lines J O, J E, intersect fig. 22.
Note 92, p. 30. Synodic motion of a satellite. Its motion during the interval between two of its consecutive eclipses.
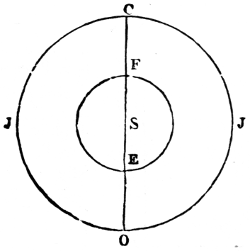
Fig. 24.
Note 93, p. 30. Opposition. A body is said to be in opposition when its longitude differs from that of the sun by 180°. If S, fig. 24, be the sun, and E the earth, then Jupiter is in opposition when at O, and in conjunction when at C. In these positions the three bodies are in the same straight line.
Note 94, p. 30. Eclipses of the 446satellites. Let S, fig. 25, be the sun, J Jupiter, and a B b his shadow. Let the earth be moving in its orbit, in the direction E A R T H, and the third satellite in the direction a b m n. When the earth is at E, the satellite, in moving through the arc a b, will vanish at a, and reappear at b, on the same side of Jupiter. If the earth be in R, Jupiter will be in opposition; and then the satellite, in moving through the arc a b, will vanish close to the disc of the planet, and will reappear on the other side of it. But, if the satellite be moving through the arc m n, it will appear to pass over the disc, and eclipse the planet.
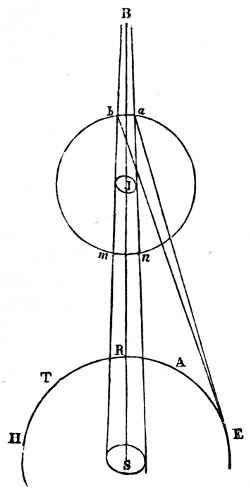
Fig. 25.
Note 95, pp. 30, 43. Meridian. A terrestrial meridian is a line passing round the earth and through both poles. In every part of it noon happens at the same instant. In figures 1 and 3, the lines N Q S and N G S are meridians, C being the centre of the earth, and N S its axis of rotation. The meridian passing through the Observatory at Greenwich is assumed by the British as a fixed origin from whence terrestrial longitudes are measured. And as each point on the surface of the earth passes through 360°, or a complete circle, in twenty-four hours, at the rate of 15° in an hour, time becomes a representative of angular motion. Hence, if the eclipse of a satellite happens at any place at eight o’clock in the evening, and the Nautical Almanac shows that the same phenomenon will take place at Greenwich at nine, the place of observation will be in the 15° of west longitude.
Note 96, p. 31. Conjunction. Let S be the sun, fig. 24, E the earth, and J O Jʹ Cʹ the orbit of Jupiter. Then the eclipses which happen when Jupiter is in O are seen 16m 26s sooner than those which take place when the planet is in C. Jupiter is in conjunction when at C, and in opposition when in O.
Fig. 26.
Note 97, p. 31. In the diagonal, &c. Were the line A S, fig. 26, 100,000 times longer than A B, Jupiter’s true place would be in the direction A Sʹ, the diagonal of the figure A B Sʹ S, which is, of course, out of proportion.
Note 98, p. 31. Aberration of light. The celestial bodies are so distant that the rays of light coming from them may be reckoned parallel. Therefore, let S A, Sʹ B, fig. 26, be two rays of light 447coming from the sun, or a planet, to the earth moving in its orbit in the direction A B. If a telescope be held in the direction A S, the ray S A, instead of going down the tube, will impinge on its side, and be lost in consequence of the telescope being carried with the earth in the direction A B. But, if the tube be held in the position A E, so that A B is to A S as the velocity of the earth to the velocity of light, the ray will pass through Sʹ E A. The star appears to be in the direction A Sʹ, when it really is in the direction A S; hence the angle S A Sʹ is the angle of aberration.
Note 99, p. 32. Density proportional to elasticity. The more a fluid, such as atmospheric air, is reduced in dimensions by pressure, the more it resists the pressure.
Note 100, p. 32. Oscillations of pendulum retarded. If a clock be carried from the pole to the equator, its rate will be gradually diminished, that is, it will go slower and slower: because the centrifugal force, which increases from the pole to the equator, diminishes the force of gravity.
Note 101, p. 34. Disturbing action. The disturbing force acts here in the very same manner as in note 63; only that the disturbing body d, fig. 14, is the sun, S the earth, and p the moon.
Note 102, pp. 35, 36, 86. Perigee. A Greek word, signifying round the earth. The perigee of the lunar orbit is the point P, fig. 6, where the moon is nearest to the earth. It corresponds to the perihelion of a planet. Sometimes the word is used to denote the point where the sun is nearest to the earth.
Note 103, p. 35. Evection. The evection is produced by the action of the radial force in the direction S p, fig. 14, which sometimes increases and sometimes diminishes the earth’s attraction to the moon. It produces a corresponding temporary change in the excentricity, which varies with the position of the major axis of the lunar orbit in respect of the line S d, joining the centres of the earth and sun.
Note 104, p. 35. Variation. The lunar perturbation called the variation is the alternate acceleration and retardation of the moon in longitude, from the action of the tangential force. She is accelerated in going from quadratures in Q and D, fig. 14, to the points C and O, called syzygies, and is retarded in going from the syzygies C and O to Q and D again.
Note 105, p. 36. Square of time. If the times increase at the rate of 1, 2, 3, 4, &c., years or hundreds of years, the squares of the times will be 1, 4, 9, 16, &c., years or hundreds of years.
Note 106, p. 37. In all investigations hitherto made with regard to the acceleration, it was tacitly assumed that the areas described by the radius vector of the moon were not permanently altered; that is to say, that the tangential disturbing force produced no permanent effect. But Mr. Adams has discovered that, in consequence of the constant decrease in the excentricity of the earth’s orbit, there is a gradual change in the central disturbing force which affects the aërial velocity, and consequently it alters the amount of the acceleration by a very small quantity, as well as the variation and other periodical inequalities of the moon. On the 448latter, however, it has no permanent effect, because it affects them in opposite directions in very moderate intervals of time, whereas a very small error in the amount of the acceleration goes on increasing as long as the excentricity of the earth’s orbit diminishes, so that it would ultimately vitiate calculations of the moon’s place for distant periods of time. This shows how complicated the moon’s motions are, and what rigorous accuracy is required in their determination.
To give an idea of the labour requisite merely to perfect or correct the lunar tables, the moon’s place was determined by observation at the Greenwich Observatory in 6000 different points of her orbit, each of which was compared with the same points calculated from Baron Plana’s formulæ, and to do that sixteen computers were constantly employed for eight years. Since the longitude is determined by the motions of the moon, the lunar tables are of the greatest importance.
Note 107, p. 37. Mean anomaly. The mean anomaly of a planet is its angular distance from the perihelion, supposing it to move in a circle. The true anomaly is its angular distance from the perihelion in its elliptical orbit. For example, in fig. 10, the mean anomaly is P C m, and the true anomaly is P S p.
Note 108, pp. 38, 68. Many circumferences. There are 360 degrees or 1,296,000 seconds in a circumference; and, as the acceleration of the moon only increases at the rate of eleven seconds in a century, it must be a prodigious number of ages before it accumulates to many circumferences.
Note 109, p. 39. Phases of the moon. The periodical changes in the enlightened part of her disc, from a crescent to a circle, depending upon her position with regard to the sun and earth.
Note 110, p. 39. Lunar eclipse. Let S, fig. 27, be the sun, E the earth, and m the moon. The space a A b is a section of the shadow, which has the form of a cone or sugar-loaf, and the spaces A a c, A b d, are the penumbra. The axis of the cone passes through A, and through E and S, the centres of the sun and earth, and n m nʹ is the path of the moon through the shadow.
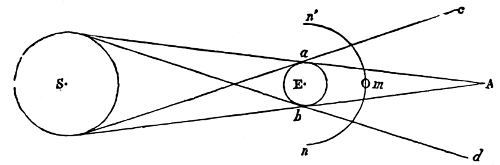
Fig. 27.
Note 111, p. 39. Apparent diameter. The diameter of a celestial body as seen from the earth.
Note 112, p. 40. Penumbra. The shadow or imperfect darkness which precedes and follows an eclipse.
449Note 113, p. 40. Synodic revolution of the moon. The time between two consecutive new or full moons.
Note 114, p. 40. Horizontal refraction. The light, in coming from a celestial object, is bent into a curve as soon as it enters our atmosphere; and that bending is greatest when the object is in the horizon.
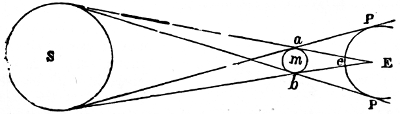
Fig. 28.
Note 115, p. 40. Solar eclipse. Let S, fig. 28, be the sun, m the moon, and E the earth. Then a E b is the moon’s shadow, which sometimes eclipses a small portion of the earth’s surface at e, and sometimes falls short of it. To a person at e, in the centre of the shadow, the eclipse may be total or annular; to a person not in the centre of the shadow a part of the sun will be eclipsed; and to one at the edge of the shadow there will be no eclipse at all. The spaces P b E, Pʹ a E, are the penumbra.
Note 116, p. 43. From the extremities, &c. If the length of the line a b, fig. 29, be measured, in feet or fathoms, the angles S b a, S a b, can be measured, and then the angle a S b is known, whence the length of the line S C may be computed. a S b is the parallax of the object S; and it is clear that, the greater the distance of S, the less the base a b will appear, because the angle a Sʹ b is less than a S b.
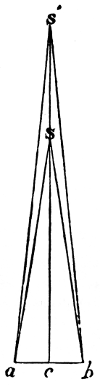
Fig. 29.
Note 117, p. 44. Every particle will describe a circle, &c. If N S, fig. 3, be the axis about which the body revolves, then particles at B, Q, &c., will whirl in the circles B G A a, Q E q d, whose centres are in the axis N S, and their planes parallel to one another. They are, in fact, parallels of latitude, Q E q d being the equator.
Note 118, p. 44. The force of gravity, &c. Gravity at the equator acts in the direction Q C, fig. 30. Whereas the direction of the centrifugal force is exactly contrary, being in the direction C Q; hence the difference of the two is the force called gravitation, which makes bodies fall to the surface of the earth. At any point, m, not at the equator, the direction of gravity is m b, perpendicular to the surface, but the centrifugal force acts perpendicularly to N S, the axis of rotation. Now the effect of the centrifugal force 450is the same as if it were two forces, one of which acting in the direction b m, diminishes the force of gravity, and another which, acting in the direction m t, tangent to the surface at m, urges the particles towards Q, and tends to swell out the earth at the equator.
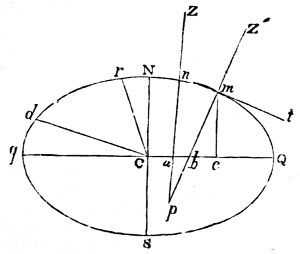
Fig. 30.
Note 119, p. 45. Homogeneous mass. A quantity of matter, everywhere of the same density.
Note 120, p. 45. Ellipsoid of revolution. A solid formed by the revolution of an ellipse about its axis. If the ellipse revolve about its minor axis Q D, fig. 6, the ellipsoid will be oblate, or flattened at the poles like an orange. If the revolution be about the greater axis A P, the ellipsoid will be prolate, like an egg.
Note 121, p. 45. Concentric elliptical strata. Strata, or layers, having an elliptical form and the same centre.
Note 122, p. 46. On the whole, &c. The line N Q S q, fig. 1, represents the ellipse in question, its major axis being Q q, its minor axis N S.
Note 123, p. 46. Increase in the length of the radii, &c. The radii gradually increase from the polar radius C N, fig. 30, which is least, to the equatorial radius C Q, which is greatest. There is also an increase in the lengths of the arcs corresponding to the same number of degrees from the equator to the poles; for, the angle N C r being equal to q C d, the elliptical arc N r is less than q d.
Note 124, p. 46. Cosine of latitude. The angles m C a, m C b, fig. 4, being the latitudes of the points a, b, &c., the cosines are C q, C r, &c.
Note 125, p. 47. An arc of the meridian. Let N Q S q, fig. 30, be the meridian, and m n the arc to be measured. Then, if Zʹ m, Z n, be verticals, or lines perpendicular to the surface of the earth, at the extremities of the arc m n they will meet in p. Q a n, Q b m, are the latitudes of the points m and n, and their difference is the angle m p n. Since the latitudes are equal to the height of the pole of the equinoctial above the horizon of the places m and n, the angle m p n may be found by observation. When the distance m n is measured in feet or fathoms, and divided by the number of degrees and parts of a degree contained in the angle m p n, the length of an arc of one degree is obtained.
Note 126, p. 47. A series of triangles. Let M Mʹ, fig. 31, be the meridian of any place. A line A B is measured with rods, on level ground, of any number of fathoms, C being some point seen from both ends of it. As two of the angles of the triangle A B C can be measured, the lengths of the sides A C, B C, can be computed; and if the angle m A B, which the 451base A B makes with the meridian, be measured, the length of the sides B m, A m, may be obtained by computation, so that A m, a small part of the meridian, is determined. Again, if D be a point visible from the extremities of the known line B C, two of the angles of the triangle B C D may be measured, and the length of the sides C D, B D, computed. Then, if the angle B m mʹ be measured, all the angles and the side B m of the triangle B m mʹ are known, whence the length of the line m mʹ may be computed, so that the portion A mʹ of the meridian is determined, and in the same manner it may be prolonged indefinitely.
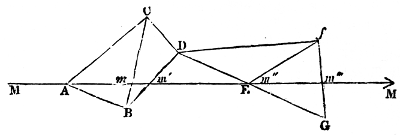
Fig. 31.
Note 127, pp. 47, 49. The square of the sine of the latitude. Q b m, fig. 30, being the latitude of m, e m is the sine and b e the cosine. Then the number expressing the length of e m, multiplied by itself, is the square of the sine of the latitude; and the number expressing the length of b e, multiplied by itself, is the square of the cosine of the latitude.
Note 128, p. 48. The polar diameter of the earth determined by the survey of Great Britain is 7900 miles; the equatorial is 7926, which gives a compression of 1⁄299·33.
Note 129, p. 50. A pendulum is that part of a clock which swings to and fro.
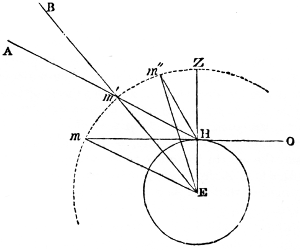
Fig. 32.
Note 130, p. 52. Parallax. The angle a S b, fig. 29, under which we view an object a b: it therefore diminishes as the distance increases. The parallax of a celestial object is the angle which the radius of the earth would be seen under, if viewed from that object. Let E, fig. 32, be the centre of the earth, E H its radius, and m H O the horizon of an observer at H. Then H m E is the parallax of a body m, the moon for example. As m rises higher and higher in the heavens to the points mʹ, mʺ, &c., the parallax H mʹ E, H mʺ E, &c., decreases. At Z, the zenith, or point immediately above the head of the observer, it is zero; and at m, where the body is in 452the horizon, the angle H m E is the greatest possible, and is called the horizontal parallax. It is clear that with regard to celestial bodies the whole effect of parallax is in the vertical, or in the direction m mʹ Z; and as a person at H sees mʹ in the direction H mʹ A, when it really is in the direction E mʹ B, it makes celestial objects appear to be lower than they really are. The distance of the moon from the earth has been determined from her horizontal parallax. The angle E m H can be measured. E H m is a right angle, and E H, the radius of the earth, is known in miles; whence the distance of the moon E m is easily found. Annual parallax is the angle under which the diameter of the earth’s orbit would be seen if viewed from a star.
Note 131, p. 52. The radii n B, n G, &c., fig. 3, are equal in any one parallel of latitude, A a B G; therefore a change in the parallax observed in that parallel can only arise from a change in the moon’s distance from the earth; and when the moon is at her mean distance, which is a constant quantity equal to half the major axis of her orbit, a change in the parallax observed in different latitudes, G and E, must arise from the difference in the lengths of the radii n G and C E.
Note 132, p. 52. When Venus is in her nodes. She must be in the line N S n where her orbit P N A n cuts the plane of the ecliptic E N e n, fig. 12.
Note 133, p. 53. The line described, &c. Let E, fig. 33, be the earth, S the centre of the sun, and V the planet Venus. The real transit of the planet, seen from E the centre of the earth, would be in the direction A B. A person at W would see it pass over the sun in the line v a, and a person at O would see it move across him in the direction vʹ aʹ.
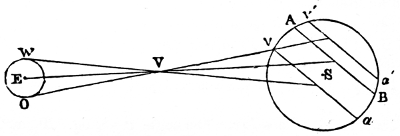
Fig. 33.
Note 134, p. 54. Kepler’s law. Suppose it were required to find the distance of Jupiter from the sun. The periodic times of Jupiter and Venus are given by observation, and the mean distance of Venus from the centre of the sun is known in miles or terrestrial radii; therefore, by the rule of three, the square root of the periodic time of Venus is to the square root of the periodic time of Jupiter as the cube root of the mean distance of Venus from the sun to the cube root of the mean distance of Jupiter from the sun, which is thus obtained in miles or terrestrial radii. The root of a number is that number which, once multiplied by itself, gives its square; twice multiplied by itself, gives its cube, &c. For example, twice 2 are 4, and twice 4 are 8; 2 is therefore the square root of 4, and the cube root of 8. In the same manner 3 times 3 are 9, and 3 times 9 are 27; 3 is therefore the square root of 9, and the cube root of 27.
Note 135, p. 55. Inversely, &c. The quantities of matter in any two 453primary planets are greater in proportion as the cubes of the numbers representing the mean distances of their satellites are greater, and also in proportion as the squares of their periodic times are less.
Note 136, p. 55. As hardly anything appears more impossible than that man should have been able to weigh the sun as it were in scales and the earth in a balance, the method of doing so may have some interest. The attraction of the sun is to the attraction of the earth as the quantity of matter in the sun to the quantity of matter in the earth; and, as the force of this reciprocal attraction is measured by its effects, the space the earth would fall through in a second by the sun’s attraction is to the space which the sun would fall through by the earth’s attraction as the mass of the sun to the mass of the earth. Hence, as many times as the fall of the earth to the sun in a second exceeds the fall of the sun to the earth in the same time, so many times does the mass of the sun exceed the mass of the earth. Thus the weight of the sun will be known if the length of these two spaces can be found in miles or parts of a mile. Nothing can be easier. A heavy body falls through 16·0697 feet in a second at the surface of the earth by the earth’s attraction; and, as the force of gravity is inversely as the square of the distance, it is clear that 16·0697 feet are to the space a body would fall through at the distance of the sun by the earth’s attraction, as the square of the distance of the sun from the earth to the square of the distance of the centre of the earth from its surface; that is, as the square of 95,000,000 miles to the square of 4000 miles. And thus, by a simple question in the rule of three, the space which the sun would fall through in a second by the attraction of the earth may be found in parts of a mile. The space the earth would fall through in a second, by the attraction of the sun, must now be found in miles also. Suppose m n, fig. 4, to be the arc which the earth describes round the sun in C, in a second of time, by the joint action of the sun and the centrifugal force. By the centrifugal force alone the earth would move from m to T in a second, and by the sun’s attraction alone it would fall through T n in the same time. Hence the length of T n, in miles, is the space the earth would fall through in a second by the sun’s attraction. Now, as the earth’s orbit is very nearly a circle, if 360 degrees be divided by the number of seconds in a sidereal year of 3651⁄4 days, it will give m n, the arc which the earth moves through in a second, and then the tables will give the length of the line C T in numbers corresponding to that angle; but, as the radius C n is assumed to be unity in the tables, if 1 be subtracted from the number representing C T, the length of T n will be obtained; and, when multiplied by 95,000,000, to reduce it to miles, the space which the earth falls through, by the sun’s attraction, will be obtained in miles. By this simple process it is found that, if the sun were placed in one scale of a balance, it would require 354,936 earths to form a counterpoise.
Note 137, p. 59. The sum of the greatest and least distances S P, S A, fig. 12, is equal to P A, the major axis; and their difference is equal to twice the excentricity C S. The longitude ♈ S P of the planet, when in the point P, at its least distance from the sun, is the longitude of the perihelion. The greatest height of the planet above the plane of the ecliptic E N e n, is equal to the inclination of the orbit P N A n to that plane. The longitude of the planet, when in the plane of the ecliptic, can only be the longitude of one of the points N or n; and, when one of these points is known, the other is given, being 180° distant from it. Lastly, 454the time included between two consecutive passages of the planet through the same node N or n, is its periodic time, allowance being made for the recess of the node in the interval.
Note 138, p. 60. Suppose that it were required to find the position of a point in space, as of a planet, and that one observation places it in n, fig. 34, another observation places it in nʹ, another in nʺ, and so on; all the points n, nʹ, nʺ, nʹʹʹ, &c., being very near to one another. The true place of the planet P will not differ much from any of these positions. It is evident, from this view of the subject, that P n, P nʹ, P nʺ, &c., are the errors of observation. The true position of the planet P is found by this property, that the squares of the numbers representing the lines P n, P nʹ, &c., when added together, is the least possible. Each line P n, P nʹ, &c., being the whole error in the place of the planet, is made up of the errors of all the elements; and, when compared with the errors obtained from theory, it affords the means of finding each. The principle of least squares is of very general application; its demonstration cannot find a place here; but the reader is referred to Biot’s Astronomy, vol. ii. p. 203.
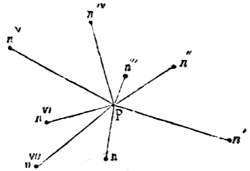
Fig. 34.
Note 139, p. 61. The true longitude of Uranus was in advance of the tables previous to 1795, and continued to advance till 1822, after which it diminished rapidly till 1830-1, when the observed and calculated longitudes agreed, but then the planet fell behind the calculated place so rapidly that it was clear the tables could no longer represent its motion.
Note 140, p. 65. An axis that, &c. Fig. 20 represents the earth revolving in its orbit about the sun in S, the axis of rotation P p being everywhere parallel to itself.
Note 141, p. 65. Angular velocities that are sensibly uniform. The earth and planets revolve about their axis with an equable motion, which is never either faster or slower. For example, the length of the day is never more nor less than twenty-four hours.
Note 142, p. 68. If fig. 1 be the moon, her polar diameter N S is the shortest; and of those in the plane of the equator, Q E q, that which points to the earth is greater than all the others.
Note 143, p. 73. Inversely proportional, &c. That is, the total amount of solar radiation becomes less as the minor axis C Cʹ, fig. 20, of the earth’s orbit becomes greater.
Note 144, p. 75. Fig. 35 represents the position of the apparent orbit of the sun as it is at present, the earth being in E. The sun is nearer to the earth in moving through ♎ P ♈ than in moving through ♈ A ♎, but its motion through ♎ P ♈ is more rapid than its motion through ♈ A ♎; and, as the swiftness of the motion and the quantity of heat received vary in the same proportion, a compensation takes place.
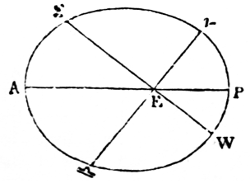
Fig. 35.
Note 145, p. 76. In an ellipsoid of revolution, 455fig. 1, the polar diameter N S, and every diameter in the equator q E Q e, are permanent axes of rotation, but the rotation would be unstable about any other. Were the earth to begin to rotate about C a, the angular distance from a to the equator at q would no longer be ninety degrees, which would be immediately detected by the change it would occasion in the latitudes.
Note 146, pp. 50, 80. Let q ♈ Q, and E ♎ e, fig. 11, be the planes of the equator and ecliptic. The angle e ♈ Q, which separates them, called the obliquity of the ecliptic, varies in consequence of the action of the sun and moon upon the protuberant matter at the earth’s equator. That action brings the point Q towards e, and tends to make the plane q ♈ Q coincide with the ecliptic E ♈ e, which causes the equinoctial points ♈ and ♎ to move slowly backwards on the plane e ♈ E, at the rate of 50ʺ·41 annually. This part of the motion, which depends upon the form of the earth, is called luni-solar precession. Another part, totally independent of the form of the earth, arises from the mutual action of the earth, planets, and sun, which, altering the position of the plane of the ecliptic e ♈ E, causes the equinoctial points ♈ and ♎ to advance at the rate of Oʺ·31 annually; but, as this motion is much less than the former, the equinoctial points recede on the plane of the ecliptic at the rate of 50ʺ·1 annually. This motion is called the precession of the equinoxes.
Note 147, p. 81. Let q ♈ Q, e ♈ E, fig. 36, be the planes of the equinoctial or celestial equator and ecliptic, and p, P, their poles. Then suppose p, the pole of the equator, to revolve with a tremulous or wavy motion in the little ellipse p c d b in about 19 years, both motions being very small, while the point a is carried round in the circle a A B in 25,868 years. The tremulous motion may represent the half-yearly variation, the motion in the ellipse gives an idea of the nutation discovered by Bradley, and the motion in the circle a A B arises from the precession of the equinoxes. The greater axis p d of the small ellipse is 18ʺ·5, its minor axis b c is 13ʺ·74. These motions are so small that they have very little effect on the parallelism of the axis of the earth’s rotation during its revolution round the sun, as represented in fig. 20. As the stars are fixed, this real motion in the pole of the earth must cause an apparent change in their places.
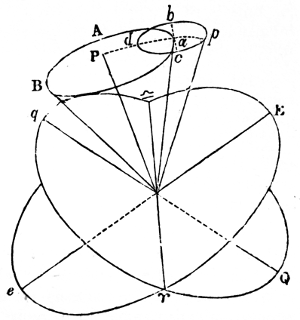
Fig. 36.
Note 148, p. 83. By means of a transit instrument, which is a telescope mounted so as to revolve only in the plane of the meridian, the instant of the transit or passage of a celestial body across the meridian can be determined. The transits of the principal stars are used to ascertain the time, or, which is the same thing, the amount of the error of clocks. A system of equidistant wires, as represented in the figure, is placed in the 456focus of the eye-piece, so that the middle wire is perpendicular and at right angles to the axis of the telescope. It consequently represents a portion of the celestial meridian; and when a star is seen to cross that wire it then crosses the celestial meridian of the place of observation. A clock beating seconds being close at hand, the duty of an observer is to note the exact second and part of a second at which a star crosses each wire successively in consequence of the rotation of the earth. Then the mean of all these observations will give the time at which the star crosses the celestial meridian of the place of observation to the tenth of a second, provided the observations are accurate. Now it happens that the simultaneous impression on the eye and ear is estimated differently by different observers, so that one person will note the transit of a star, for example, as happening the fraction of a second sooner or later than another person; and as that is the case in every observation he makes, it is called his personal equation, that is to say, it is a correction that must be applied to all the observations of the individual, and a curious instance of individuality it is. For instance, M. Otto Struve notes every observation Oʺ·11 too soon, M. Peters Oʺ·13 too late; M. Struve noted every observation one second later than M. Bessel, and M. Argelander estimated the transit of a star 1ʺ·2 later than M. Bessel. All these gentlemen were or are first-rate observers; and when the personal equation is known it is easy to correct the observations. However, to avoid that inconvenience Mr. Bond has introduced a method in the Observatory at Cambridge in the United States in which touch is combined with sight instead of hearing, which is now used also at Greenwich. The observer at the moment of the observation presses his fingers on a machine which by means of a galvanic battery conveys the impression to where time is measured and marked, so that the observation is at once recorded and the personal equation avoided.
Note 149, p. 84. Let N be the pole, fig. 11, e E the ecliptic, and Q q the equator. Then, N n m S being a meridian, and at right angles to the equator, the arc ♈ m is less than the arc ♈ n.
Note 150, p. 85. Heliacal rising of Sirius. When the star appears in the morning, in the horizon, a little before the rising of the sun.
Note 151, p. 87. Let P ♈ A ♎, fig. 35, be the apparent orbit or path of the sun, the earth being in E. Its major axis, A P, is at present situate as in the figure, where the solar perigee P is between the solstice of winter and the equinox of spring. So that the time of the sun’s passage through the arc ♈ A ♎ is greater than the time he takes to go through the arc ♎ P ♈. The major axis A P coincided with ♎ ♈, the line of the equinoxes, 4000 years before the Christian era; at that time P was in the point ♈. In 6468 of the Christian era the perigee P will coincide with ♎. In 1234 A.D. the major axis was perpendicular to ♈ ♎, and then P was in the winter solstice.
Note 152, p. 88. At the solstices, &c. Since the declination of a celestial object is its angular distance from the equinoctial, the declination of the sun at the solstice is equal to the arc Q e, fig. 11, which measures the obliquity of the ecliptic, or angular distance of the plane ♈ e ♎ from the plane ♈ Q ♎.
Note 153, p. 88. Zenith distance is the angular distance of a celestial object from the point immediately over the head of an observer.
457Note 154, p. 89. Reduced to the level of the sea. The force of gravitation decreases as the square of the height above the surface of the earth increases, so that a pendulum vibrates slower on high ground; and, in order to have a standard independent of local circumstances, it is necessary to reduce it to the length that would exactly make 86,400 vibrations in a mean solar day at the level of the sea.
Note 155, p. 90. A quadrant of the meridian is a fourth part of a meridian, or an arc of a meridian containing 90°, as N Q, fig. 11.
Note 156, p. 93. Moon’s southing. The time when the moon is on the meridian of any place, which happens about forty-eight minutes later every day.
Note 157, p. 96. The angular velocity of the earth’s rotation is at the rate of 180° in twelve hours, which is the time included between the passages of the moon at the upper and under meridian.
Note 158, p. 96. If S be the earth, fig. 14, d the sun, and C Q O D the orbit of the moon, then C and O are the syzygies. When the moon is new, she is at C, and when full she is at O; and, as both sun and moon are then on the same meridian, it occasions the spring-tides, it being high water at places under C and O, while it is low water at those under Q and D. The neap-tides happen when the moon is in quadrature at Q or D, for then she is distant from the sun by the angle d S Q, or d S D, each of which is 90°.
Note 159, p. 97. Declination. If the earth be in C, fig. 11, and if q ♈ Q be the equinoctial, and N m S a meridian, then m C n is the declination of a body at n. Therefore the cosine of that angle is the cosine of the declination.
Note 160, pp. 99, 131. Fig 37 shows the propagation of waves from two points C and Cʹ, where stones are supposed to have fallen. Those points in which the waves cross each other are the places where they counteract each other’s effects, so that the water is smooth there, while it is agitated in the intermediate spaces.
Note 161, p. 100. The centrifugal force may, &c. The centrifugal force acts in a direction at right angles to N S, the axis of rotation, fig. 30. Its effects are equivalent to two forces, one of which is in the direction b m perpendicular to the surface Q m n of the earth, and diminishes the force of gravity at m. The other acts in the direction of the tangent m T, which makes the fluid particles tend towards the equator.
Fig. 37.
458Note 162, p. 106. Analytical formula or expression. A combination of symbols or signs expressing or representing a series of calculation, and including every particular case that can arise from a general law.
Note 163, p. 106. Fig. 38 is a perfect octahedron. Sometimes its angles, A, X, a, a, &c., are truncated, or cut off. Sometimes a slice is cut off its edges A a, X a, a a, &c. Occasionally both these modifications take place.
Fig. 38.
Note 164, p. 107. Prismatic crystals of sulphate of nickel are somewhat like fig. 62, only that they are thin, like a hair.
Note 165, p. 108. Zinc, a metal either found as an ore or mixed with other metals. It is used in making brass.
Note 166, p. 108. A cube is a solid contained by six plane square surfaces, as fig. 39.
Fig. 39.
Note 167, p. 108. A tetrahedron is a solid contained by four triangular surfaces, as fig. 40: of this solid there are many varieties.
Fig. 40.
Note 168, p. 108. There are many varieties of the octahedron. In that mentioned in the text, the base a a a a, fig. 38, is a square, but the base may be a rhomb; this solid may also be elongated in the direction of its axis A X, or it may be depressed.
Note 169, pp. 109, 192, 273. A rhombohedron is a solid contained by six plane surfaces, as in fig. 63, the opposite planes being equal and similar rhombs parallel to one another; but all the planes are not necessarily equal or similar, nor are its angles right angles. In carbonate of lime the angle C A B is 105°·55, and the angle B or C is 75°·05.
Note 170, p. 109. Sublimation. Bodies raised into vapour which is again condensed into a solid state.
Note 171, p. 112. Platinum. The heaviest of metals; its colour is between that of silver and lead.
Note 172, p. 113. The surface of a column of water, or spirit of 459wine, in a capillary tube, is hollow; and that of a column of quicksilver is convex, or rounded, as in fig. 41.
Note 173, p. 113. Inverse ratio, &c. The elevation of the liquid is greater in proportion as the internal diameter of the tube is less.
Note 174, p. 114. In fig. 41 the line c d shows the direction of the resulting force in the two cases.
Fig. 41.
Note 175, p. 115. When two plates of glass are brought near to one another in water, the liquid rises between them; and, if the plates touch each other at one of their upright edges, the outline of the water will become an hyperbola.
Note 176, p. 115. Let A Aʹ, fig. 42, be two plates, both of which are wet, and B Bʹ two that are dry. When partly immersed in a liquid, its surface will be curved close to them, but will be of its usual level for the rest of the distance. At such a distance they will neither attract nor repel one another. But, as soon as they are brought near enough to have the whole of the liquid surface between them curved, as in a aʹ, b bʹ, they will rush together. If one be wet and another dry, as C Cʹ, they will repel one another at a certain distance; but, as soon as they are brought very near, they will rush together, as in the former cases.
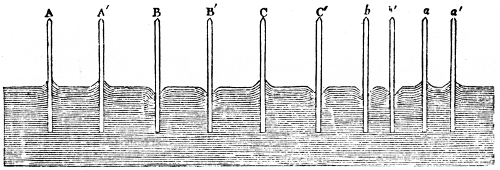
Fig. 42.
Note 177, p. 123. In a paper on the atmospheric changes that produce rain and wind, by Thomas Hopkins, Esq., in the Geographical Journal, it is shown that, when vapour is condensed and falls in rain, a partial vacuum is formed, and that heavier air presses in as a current of wind. Thus the vacuum arising from the great precipitation at the tropics causes the polar winds to descend from the upper regions of the atmosphere and blow along the surface to the equator as trade winds to supply the place of the hot currents that are continually raising them into the higher regions. This circumstance removes the only difficulty in Lieutenant Maury’s theory of the winds.
Note 178, p. 134. Latent or absorbed heat. There is a certain quantity of heat in all bodies, which cannot be detected by the thermometer, but which may become sensible by compression.
460Note 179, p. 137. Reflected waves. A series of waves of light, sound, or water, diverge in all directions from their origin I, fig. 43, as from a centre. When they meet with an obstacle S S, they strike against it, and are reflected or turned back by it in the same form as if they had proceeded from the centre C, at an equal distance on the other side of the surface S S.
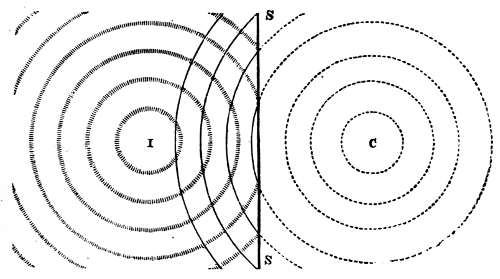
Fig. 43.
Note 180, p. 138. Elliptical shell. If fig. 6 be a section of an elliptical shell, then all sounds coming from the focus S to different points on the surface, as m, are reflected back to F, because the angle T m S is equal to t m F. In a spherical hollow shell, a sound diverging from the centre is reflected back to the centre again.
Note 181, p. 142. Fig. 44 represents musical strings in vibration; the straight lines are the strings when at rest. The first figure of the four would give the fundamental note, as, for example, the low C. The second and third figures would give the first and second harmonics; that is, the octave and the 12th above C, n n n being the points at rest; the fourth figure shows the real motion when compounded of all three.
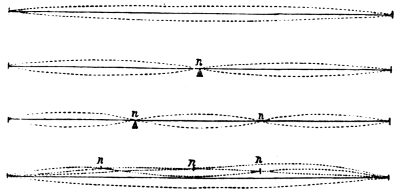
Fig. 44.
461Note 182, p. 143. Fig. 45 represents sections of an open and of a shut pipe, and of a pipe open at one end. When sounded, the air spontaneously divides itself into segments. It remains at rest in the divisions or nodes n nʹ, &c., but vibrates between them in the direction of the arrow-heads. The undulations of the whole column of air give the fundamental note, while the vibrations of the divisions give the harmonics.
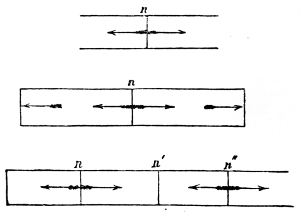
Fig. 45.
Note 183, p. 144. Fig. 1, plate 1, shows the vibrating surface when the sand divides it into squares, and fig. 2 represents the same when the nodal lines divide it into triangles. The portions marked a a are in different states of vibration from those marked b b.
Note 184, p. 145. Plates 1 and 2 contain a few of Chladni’s figures. The white lines are the forms assumed by the sand, from different modes of vibration, corresponding to musical notes of different degrees of pitch. Plate 3 contains six of Chladni’s circular figures.
Note 185, p. 145. Mr. Wheatstone’s principle is, that when vibrations producing the forms of figs. 1 and 2, plate 3, are united in the same surface, they make the sand assume the form of fig. 3. In the same manner, the vibrations which would separately cause the sand to take the forms of figs. 4 and 5, would make it assume the form in fig. 6 when united. The figure 9 results from the modes of vibration of 7 and 8 combined. The parts marked a a are in different states of vibration from those marked b b. Figs. 1, 2, and 3, plate 4, represent forms which the sand takes in consequence of simple modes of vibration; 4 and 5 are those arising from two combined modes of vibration; and the last six figures arise from four superimposed simple modes of vibration. These complicated figures are determined by computation independent of experiment.
Note 186, p. 146. The long cross-lines of fig. 46 show the two systems of nodal lines given by M. Savart’s laminæ.
Fig. 46.
Note 187, p. 146. The short lines on fig. 46 show the positions of the nodal lines on the other sides of the same laminæ.
Note 188, p. 146. Fig. 47 gives the nodal lines on a cylinder, with the paper rings that mark the quiescent points.

Fig. 47.
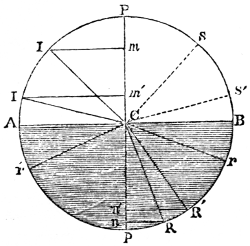
Fig. 48.
Note 189, pp. 138, 153, 156. Reflection and Refraction. Let P C p, fig. 48, be perpendicular to a surface of glass or water A B. When a ray of light, passing through the air, falls on this surface in any direction I C, part of it is reflected in the direction C S, and the other part is bent at C, and passes through the glass or water in the direction C R. I C is called the incident ray, and I C P the angle of incidence; C S is the reflected ray, and P C S the angle of reflection; C R is the refracted ray, and p C R the angle of refraction. The plane passing through S C and I C is the plane of reflection, and the plane passing through I C and C R is the plane of refraction. In ordinary cases, C I, C S, C R, are all in the same plane. We see the surface by means of the reflected light, which would otherwise be invisible. Whatever the reflecting surface may be, and however obliquely the light may fall upon it, the angle of reflection is always equal to the angle of incidence. Thus I C, Iʹ C, being rays incident on the surface at C, they will be reflected into C S, C Sʹ, so that the angle S C P will be equal to the angle I C P, and Sʹ C P equal to Iʹ C P. That is by no means the case with the refracted rays. The incident rays I C, Iʹ C, are bent at C towards the perpendicular, in the direction C R, C Rʹ; and the law of refraction is such, that the sine of the angle of incidence has a constant ratio to the sine of the angle of refraction; that is to say, the number expressing the length of I m, the sine of I C P, divided by the number expressing the length of R n, the sine of R C p, is the same for all the rays of light that can fall upon the surface of any one substance, and is called its index of refraction. Though the index of refraction be the same for any one substance, it is not the same for all substances. For water it is 1·336; for crown-glass it is 1·535; for flint-glass, 1·6; for diamond, 2·487; and for chromate of lead it is 3, which substance has a higher refractive power than any other known. Light falling perpendicularly on a surface passes through it without being refracted. If the light be now supposed to pass from a dense into a rare medium, as from glass or water into air, then R C, Rʹ C, become the incident rays; and in this case the refracted rays, C I, C Iʹ, are bent from the perpendicular instead of towards it. When the incidence is very oblique, as r C, the light never passes into the air at all, but it is totally reflected in the direction C rʹ, so that the angle p C r is equal to p C rʹ; that frequently happens at the second surface of glass. When a ray I C falls from air upon a piece of glass A B, it is in general refracted at each surface. At C it is bent towards the perpendicular, and at R from it, and the ray emerges parallel to I C; but, when the ray is very oblique to the second surface, it is totally reflected. An object seen by total reflection is nearly as vivid as when seen by direct vision, because no part of the light is refracted. When light falls upon a plate of crown-glass, at an angle of 4° 32ʹ counted from the surface, the glass reflects 4 times more light than it transmits. At an angle of 7° 1ʹ the reflected light is double of the transmitted; at an angle of 11° 8ʹ the light reflected is equal to that transmitted; at 17° 17ʹ the reflected is 463equal to 1⁄2 the transmitted light; at 26° 38ʹ it is equal to 1⁄4, the variation, according to Arago, being as the square of the cosine.
Note 189, p. 154. Atmospheric refraction. Let a b, a b, &c., fig. 49, be strata, or extremely thin layers, of the atmosphere, which increase in density towards m n, the surface of the earth. A ray coming from a star meeting the surface of the atmosphere at S would be refracted at the surface of each layer, and would consequently move in the curved line S v v v A; and as an object is seen in the direction of the ray that meets the eye, the star, which really is in the direction A S, would seem to a person at A to be in s. So that refraction, which always acts in a vertical direction, raises objects above their true place. For that reason, a body at Sʹ, below the horizon H A O, would be raised, and would be seen in sʹ. The sun is frequently visible by refraction after he is set, or before he is risen. There is no refraction in the zenith at Z. It increases all the way to the horizon, where it is greatest, the variation being proportional to the tangent of the angles Z A S, Z A Sʹ, the distances of the bodies S Sʹ from the zenith. The more obliquely the rays fall, the greater the refraction.
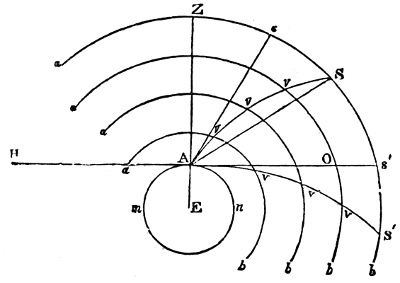
Fig. 49.
Fig. 50.
Note 190, p. 154. Bradley’s method of ascertaining the amount of refraction. Let Z, fig. 50, be the zenith or point immediately above an observer at A; let H O be his horizon, and P the pole of the equinoctial A Q. Hence P A Q is a right angle. A star as near to the pole as s would appear to revolve about it, in consequence of the rotation of the earth. At noon, for example, it would be at s above the pole, and at midnight it would be in sʹ below it. The sum of the true zenith distances, Z A s, Z A sʹ, is equal 464to twice the angle Z A P. Again, S and Sʹ being the sun at his greatest distances from the equinoctial A Q when in the solstices, the sum of his true zenith distances, Z A S, Z A Sʹ, is equal to twice the angle Z A Q. Consequently, the four true zenith distances, when added together, are equal to twice the right angle Q A P; that is, they are equal to 180°. But the observed or apparent zenith distances are less than the true on account of refraction; therefore the sum of the four apparent zenith distances is less than 180° by the whole amount of the four refractions.
Note 191, p. 155. Terrestrial refraction. Let C, fig. 51, be the centre of the earth, A an observer at its surface, A H his horizon, and B some distant point, as the top of a hill. Let the arc B A be the path of a ray coming from B to A; E B, E A, tangents to its extremities; and A G, B F, perpendicular to C B. However high the hill B may be, it is nothing when compared with C A, the radius of the earth; consequently, A B differs so little from A D that the angles A E B and A C B are supplementary to one another; that is, the two taken together are equal to 180°. A C B is called the horizontal angle. Now B A H is the real height of B, and E A H its apparent height; hence refraction raises the object B, by the angle E A B, above its real place. Again, the real depression of A, when viewed from B, is F B A, whereas its apparent depression is F B E, so E B A is due to refraction. The angle F B A is equal to the sum of the angles B A H and A C B; that is, the true elevation is equal to the true depression and the horizontal angle. But the true elevation is equal to the apparent elevation diminished by the refraction; and the true depression is equal to the apparent depression increased by refraction. Hence twice the refraction is equal to the horizontal angle augmented by the difference between the apparent elevation and the apparent depression.
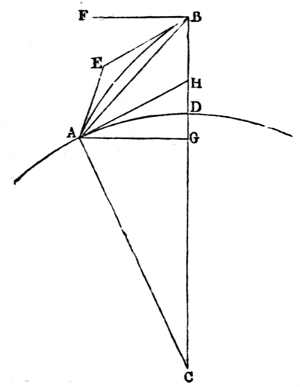
Fig. 51.
Note 192, p. 155. Fig. 52 represents the phenomenon in question. S P is the real ship, with its inverted and direct images seen in the air. Were there no refraction, the rays would come from the ship S P to the eye E in the direction of the straight lines; but, on account of the variable density of the inferior strata of the atmosphere, the rays are bent in the curved lines P c E, P d E, S m E, S n E. Since an object is seen in the direction of the tangent to that point of the ray which meets the eye, the point P of the real ship is seen at p and pʹ, and the point S seems to be in s and sʹ; and, as all the other points are transferred in the same manner, direct and inverted images of the ship are formed in the air above it.
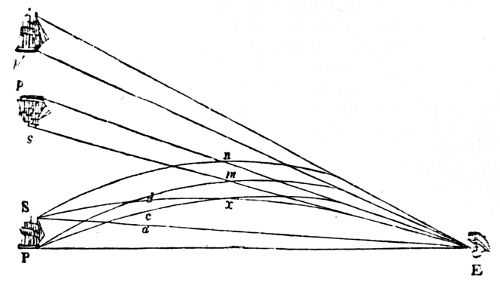
Fig. 52.
Note 193, p. 156. Fig. 53 represents the section of a poker, with the refraction produced by the hot air surrounding it.
Fig. 53.
Note 194, p. 156. The solar spectrum. A ray from the sun at S, fig. 54, admitted into a dark room, through a small round hole H in a window-shutter, proceeds in a straight line to a screen D, on which it forms a bright circular spot of white light, of nearly the same diameter with the hole H. But when the refracting angle B A C of a glass prism is interposed, so that the sunbeam falls on A C the first surface of the prism, and emerges from the second surface A B at equal angles, it causes the rays to deviate from the straight path S D, and bends them to the screen M N, where they form a coloured image V R of the sun, of the same breadth with the diameter of the hole H, but much longer. The space V R consists of seven colours—violet, indigo, blue, green, yellow, orange, and red. The violet and red, being the most and least refrangible rays, are at the extremities, and the green occupy the middle part at G. The angle D g G is called the mean deviation, and the spreading of the coloured rays over the angle V g R the dispersion. The deviation and dispersion vary with the refracting angle B A C of the prism, and with the substance of which it is made.
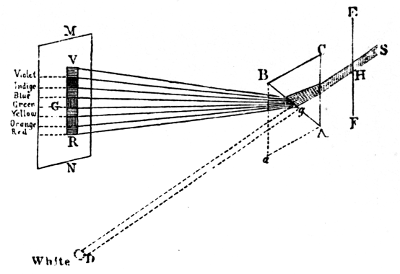
Fig. 54.
466Note 195, pp. 159, 164. Under the same circumstances, and where the refracting angles of the two prisms are equal, the angles D g G and V g R, fig. 54, are greater for flint-glass than for crown-glass. But, as they vary with the angle of the prism, it is only necessary to augment the refracting angle of the crown-glass prism by a certain quantity, to produce nearly the same deviation and dispersion with the flint-glass prism. Hence, when the two prisms are placed with their refracting angles in opposite directions, as in fig. 54, they nearly neutralize each other’s effects, and refract a beam of light without resolving it into its elementary coloured rays. Sir David Brewster has come to the conclusion that there may be refraction without colour by means of two prisms, or two lenses, when properly adjusted, even though they be made of the same kind of glass.
Note 196, p. 165. The object glass of the achromatic telescope consists of a convex lens A B, fig. 55, of crown-glass placed on the outside, towards the object, and of a concave-convex lens C D of flint-glass, placed towards the eye. The focal length of a lens is the distance of its centre from the point in which the rays converge, as F, fig. 60. If, then, the lenses A B and C D be so constructed that their focal lengths are in the same proportion as their dispersive powers, they will refract rays of light without colour.
Fig. 55.
Note 197, p. 165. If the mean refracting angle of the prism D g G, fig. 54, were the same for all substances, then the difference D g V - D g R would be the dispersion. But the angle of the prism being the same, all these angles are different in each substance, so that in order to obtain the dispersion of any substance the angle D g V - D g R must be divided by the angle D g G or its excess above unity, to which the mean refraction is always proportional. According to Mr. Fraunhofer the refraction of the extreme violet and red rays in crown-glass is 1·5466 and 1·5258; so D g V - D g R = 1·5466 - 1·5258 = ·0208, and half the sum of the excess of each above unity is = ·5362; consequently
so that the dispersive power of diamond is a little less than that of crown-glass; hence the splendid refracted colours which distinguish diamond from every other precious stone are not owing to its high dispersive power, but to its great mean refraction.—Sir David Brewster.
Note 198, p. 168. When a sunbeam, after having passed through a coloured glass V Vʹ, fig. 56, enters a dark room by two small slits O Oʹ in a card, or piece of tin, they produce alternate bright and black bands on a screen S Sʹ at a little distance. When either one or other of the slits O or Oʹ is stopped, the dark bands vanish, and the screen is illuminated by a uniform light, proving that the dark bands are produced by the interference of the two sets of rays. Again, let H m, fig. 57, be a beam of white light 467passing through a hole at H, made with a fine needle in a piece of lead or a card, and received on a screen S Sʹ. When a hair, or a small slip of card h hʹ, about the 30th of an inch in breadth, is held in the beam, the rays bend round on each side of it, and, arriving at the screen in different states of vibration, interfere and form a series of coloured fringes on each side of a central white band m. When a piece of card is interposed at C, so as to intercept the light which passes on one side of the hair, the coloured fringes vanish. When homogeneous light is used, the fringes are broadest in red, and become narrower for each colour of the spectrum progressively to the violet, which gives the narrowest and most crowded fringes. These very elegant experiments are due to Dr. Thomas Young.
Fig. 56.
Fig. 57.
Fig. 58.
Note 199, pp. 171, 200. Fig. 58 shows Newton’s rings, of which there are seven, formed by screwing two lenses of glass together. Provided the incident light be white, they always succeed each other in the following order:—
1st ring, or 1st order of colours: Black, very faint blue, brilliant white, yellow, orange, red.
2nd ring: Dark purple, or rather violet, blue, a very imperfect yellow green, vivid yellow, crimson red.
3rd ring: Purple, blue, rich grass green, fine yellow, pink, crimson.
4th ring: Dull blueish green, pale yellowish pink, red.
4685th ring: Pale blueish green, white, pink.
6th ring: Pale blue green, pale pink.
7th ring: Very pale blueish green, very pale pink.
After the seventh order the colours become too faint to be distinguished. The rings decrease in breadth, and the colours become more crowded together, as they recede from the centre. When the light is homogeneous, the rings are broadest in the red, and decrease in breadth with every successive colour of the spectrum to the violet.
Note 200, p. 172. The absolute thickness of the film of air between the glasses is found as follows:—Let A F B C, fig. 59, be the section of a lens lying on a plane surface or plate of glass P Pʹ, seen edgewise, and let E C be the diameter of the sphere of which the lens is a segment. If A B be the diameter of any one of Newton’s rings, and B D parallel to C E, then B D or C F is the thickness of the air producing it. E C is a known quantity; and when A B, the diameter, is measured with compasses, B D or F C can be computed. Newton found that the length of B D, corresponding to the darkest part of the first ring, is the 98,000th part of an inch when the rays fall perpendicularly on the lens, and from this he deduced the thickness corresponding to each colour in the system of rings. By passing each colour of the solar spectrum in succession over the lenses, Newton also determined the thickness of the film of air corresponding to each colour, from the breadth of the rings, which are always of the same colour with the homogeneous light.
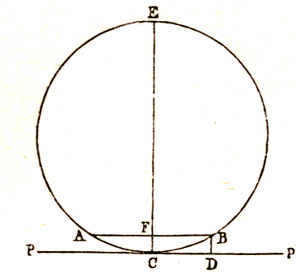
Fig. 59.
Note 201, p. 174. The focal length or distance of a lens is the distance from its centre to the point F, fig. 60, in which the refracted rays meet. Let L Lʹ be a lens of very short focal distance fixed in the window-shutter of a dark room. A sunbeam S L Lʹ passing through the lens will be brought to a focus in F, whence it will diverge in lines F C, F D, and will form a circular image of light on the opposite wall. Suppose a sheet of lead, having a small pin-hole pierced through it, to be placed in this beam; when the pin-hole is viewed from behind with a lens at E, it is surrounded with a series of coloured rings, which vary in appearance with the relative positions of the pin-hole and eye with regard to the point F. When the hole is the 30th of an inch in diameter and at the distance of 61⁄2 feet from F, when viewed at the distance of 24 inches, there are seven rings of the following colours:—
1st order: White, pale yellow, yellow, orange, dull red.
2nd order: Violet, blue, whitish, greenish yellow, fine yellow, orange red.
3rd order: Purple, indigo blue, greenish blue, brilliant green, yellow green, red.
4th order: Blueish green, blueish white, red.
5th order: Dull green, faint blueish white, faint red.
4696th order: Very faint green, very faint red.
7th order: A trace of green and red.
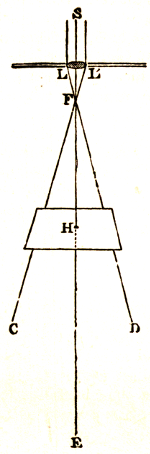
Fig. 60.
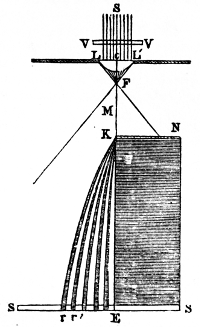
Fig. 61.
Fig. 62.
Note 202, p. 175. Let L Lʹ, fig. 61, be the section of a lens placed in a window-shutter, through which a very small beam of light S L Lʹ passes into a dark room, and comes to a focus in F. If the edge of a knife K N be held in the beam, the rays bend away from it in hyperbolic curves K r, K rʹ, &c., instead of coming directly to the screen in the straight line K E, which is the boundary of the shadow. As these bending rays arrive at the screen in different states of undulation, they interfere, and form a series of coloured fringes, r rʹ, &c., along the edge of the shadow K E S N of the knife. The fringes vary in breadth with the relative distances of the knife-edge and screen from F.
Note 203, p. 177. Fig. 43 represents the phenomena in question, where S S is the surface, and I the centre of incident waves. The reflected waves are the dark lines returning towards I, which are the same as if they had originated in C on the other side of the surface.
Note 204, p. 180. Fig. 62 represents a prismatic crystal of tourmaline, whose axis is A X. The slices that are used for polarising light are cut parallel to A X.
Note 205, p. 181. Double refraction. If a pencil of light R r, fig. 63, falls upon a rhombohedron of Iceland spar A B X C, it is separated into two equal pencils of light at r, which are refracted in the directions r O, r E: when these arrive at O and E they are again refracted, and pass into the air in the directions O o, E o, parallel to one another and to the 470incident ray R r. The ray r O is refracted according to the ordinary law, which is, that the sines of the angles of incidence and refraction bear a constant ratio to one another (see Note 184), and the rays R r, r O, O o, are all in the same plane. The pencil r E, on the contrary, is bent aside out of that plane, and its refraction does not follow the constant ratio of the sines; r E is therefore called the extraordinary ray, and r O the ordinary ray. In consequence of this bisection of the light, a spot of ink at O is seen double at O and E, when viewed from r I; and when the crystal is turned round, the image E revolves about O, which remains stationary.
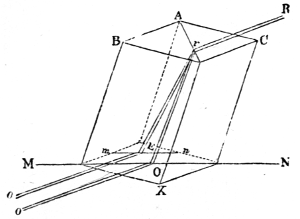
Fig. 63.
Note 206, p. 182. Both of the parallel rays O o and E o, fig. 63, are polarised on leaving the doubly refracting crystal, and in both the particles of light make their vibrations at right angles to the lines O o, E o. In the one, however, these vibrations lie, for example, in the plane of the horizon, while the vibrations of the other lie in the vertical plane perpendicular to the horizon.
Note 207, p. 183. If light be made to fall in various directions on the natural faces of a crystal of Iceland spar, or on faces cut and polished artificially, one direction A X, fig. 63, will be found, along which the light passes without being separated into two pencils. A X is the optic axis. In some substances there are two optic axes forming an angle with each other. The optic axis is not a fixed line, it only has a fixed direction; for if a crystal of Iceland spar be divided into smaller crystals, each will have its optic axis; but if all these pieces be put together again, their optic axes will be parallel to A X. Every line, therefore, within the crystal parallel to A X is an optic axis; but as these lines have all the same direction, the crystal is still said to have but one optic axis.
Note 208, p. 184. If I C, fig. 48, be the incident and C S the reflected rays, then the particles of polarised light make their vibrations at right angles to the plane of the paper.
Note 209, p. 184. Let A A, fig. 48, be the surface of the reflector, I C the incident and C S the reflected rays; then, when the angle S C B is 57°, and consequently the angle P C S equal to 33°, the black spot will be seen at C by an eye at S.
Note 210, p. 185. Let A B, fig. 48, be a reflecting surface, I C the incident and C S the reflected rays; then, if the surface be plate-glass, the angle S C B must be 57°, in order that C S may be polarised. If the surface be crown-glass or water, the angle S C B must be 56° 55ʹ for the first, and 53° 11ʹ for the second, in order to give a polarised ray.
Note 211, p. 186. A polarising apparatus is represented in fig. 64, where R r is a ray of light falling on a piece of glass r at an angle of 57°: 471the reflected ray r s is then polarised, and may be viewed through a piece of tourmaline in s, or it may be received on another plate of glass, B, whose surface is at right angles to the surface of r. The ray r s is again reflected in s, and comes to the eye in the direction s E. The plate of mica, M I, or of any substance that is to be examined, is placed between the points r and s.
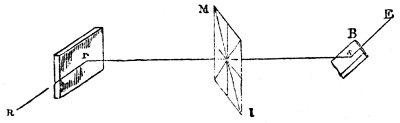
Fig. 64.
Note 212, p. 187. In order to see these figures, the polarised ray r s, fig. 64, must pass through the optic axis of the crystal, which must be held as near as possible to s on one side, and the eye placed as near as possible to s on the other. Fig. 65 shows the image formed by a crystal of Iceland spar which has one optic axis. The colours in the rings are exactly the same with those of Newton’s rings given in Note 199, and the cross is black. If the spar be turned round its axis, the rings suffer no change; but if the tourmaline through which it is viewed, or the plate of glass, B, be turned round, this figure will be seen at the angles 0°, 90°, 180°, and 270° of its revolution. But in the intermediate points, that is, at the angles 45°, 135°, 225°, and 315°, another system will appear, such as represented in fig. 66, where all the colours of the rings are complementary to those of fig. 65, and the cross is white. The two systems of rings, if superposed, would produce white light.
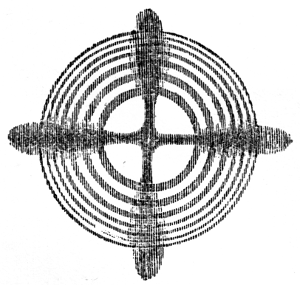
Fig. 65.
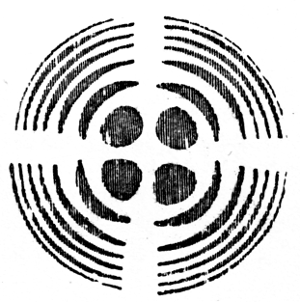
Fig. 66.
Note 213, p. 188. Saltpetre, or nitre, crystallises in six-sided prisms having two optic axes inclined to one another at an angle of 5°. A slice of this substance about the 6th or 8th of an inch thick, cut perpendicularly to the axis of the prism, and placed very near to s, fig. 64, so that the 472polarised ray r s may pass through it, exhibits the system of rings represented in fig. 67, where the points C and C mark the position of the optic axes. When the plate B, fig. 64, is turned round, the image changes successively to those given in figs. 68, 69, and 70. The colours of the rings are the same with those of thin plates, but they vary with the thickness of the nitre. Their breadth enlarges or diminishes also with the colour, when homogeneous light is used.
Fig. 67.
Fig. 68.
Fig. 69.
Fig. 70.
Fig. 71.
Note 214, p. 189. Fig. 71 represents the appearance produced by 473placing a slice of rock crystal in the polarised ray r s, fig. 64. The uniform colour in the interior of the image depends upon the thickness of the slice; but whatever that colour may be, it will alternately attain a maximum brightness and vanish with the revolution of the glass B. It may be observed, that the two kinds of quartz, or rock crystal, mentioned in the text, are combined in the amethyst, which consists of alternate layers of right-handed and left-handed quartz, whose planes are parallel to the axis of the crystal.
Note 215, p. 193. Suppose the major axis A P of an ellipse, fig. 18, to be invariable, but the excentricity C S continually to diminish, the ellipse would bulge more and more; and when C S vanished, it would become a circle whose diameter is A P. Again, if the excentricity were continually to increase, the ellipse would be more and more flattened till C S was equal to C P, when it would become a straight line A P. The circle and straight line are therefore the limits of the ellipse.
Note 216, p. 194. The coloured rings are produced by the interference of two polarised rays in different states of undulation, on the principle explained for common light.
Note 217, p. 225. According to Mr. Joule, that heat is produced by motion, and that it is equivalent to it, Mr. Thompson of Glasgow investigates from whence the sun derives his heat, since he shows that neither combustion nor his primitive heat could have supplied the waste during 6000 years. He concludes that the solar heat is maintained by myriads of minute bodies that are revolving at the edge of his dense nebulosity or atmosphere, some of which are often seen by us as falling stars. These, vaporized by his heat, and drawn by his attraction, meet with intense resistance on entering the solar atmosphere as a shower of meteoric rain; through it they descend in spiral lines to the sun’s surface, producing enormous heat by friction during their fall, and serving for fuel on their arrival.
Note 218, p. 252. The class Cryptogamia contains the ferns, mosses, funguses, and sea-weeds; in all of which the parts of the flowers are in general too minute to be evident.
Note 219, p. 254. Zoophytes are the animals which form madrepores, corals, sponges, &c.
Note 220, p. 254. The Saurian tribe are creatures of the crocodile and lizard kind.
Note 221, p. 266. If heat from a non-luminous source be polarised by reflection or refraction at r, fig. 64, the polarised ray r s will be stopped or transmitted by a plate of mica M I, under the same circumstances that it would stop or transmit light; and if heat were visible, images analogous to those of figs. 65, 67, &c., would be seen at the point s.
Note 222, pp. 275, 329, 357. The foot-pound, or unit of mechanical force established by Mr. Joule, is the force that would raise one pound weight of matter to the height of one foot; or it is the impetus or force generated by a body of one pound weight falling by its gravitation through the height of one foot.
474Impetus, vis viva, or living force, is equal to the mass of a body multiplied by the square of the velocity with which it is moving, and is the true measure of work or labour. For if a weight be raised 10 feet, it will require four times the labour to raise an equal weight 40 feet. If both these weights be allowed to descend freely by their gravitation, at the end of their fall their velocities will be as 1 to 2; that is, as the square roots of their heights; but the effect produced will be as their masses multiplied by 1 and 4; but these are the squares of their velocities: hence the impetus or vis viva is as the mass into the square of the velocity.
Thus impetus is the true measure of the labour employed to raise the weights, and of the effect of their descent, and is entirely independent of time. Now heat is proportional to impetus, and impetus is the true measure of labour. In percussion the heat evolved is in proportion to the force of the impetus, and is thus measured by labour.
Travail is a word used in mechanics, to express that work done is equal to the labouring force employed. The work done may be resistance overcome or any other effect produced, while the labouring force may be a horse, a steam-engine, wind, falling water, &c.
Note 223, p. 313. When a stream of positive electricity descends from P to n, fig. 72, in a vertical wire at right angles to the plane of the horizontal circle A B, the negative electricity ascends from n to P, and the force exerted by the current makes the north pole of a magnet revolve about the wire in the direction of the arrow-heads in the circumference, and it makes the south pole revolve in the opposite direction. When the current of positive electricity flows upwards from n to P, these effects are reversed.
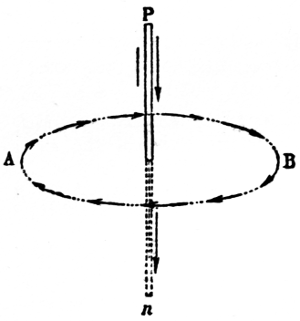
Fig. 72.
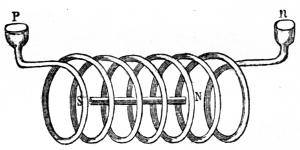
Fig. 73.
Note 224, p. 314. Fig. 73 represents a helix or coil of copper wire, terminated by two cups containing a little quicksilver. When the positive wire of a Voltaic battery is immersed in the cup p, and the negative wire in the cup n, the circuit is completed. The quicksilver ensures the connection between the battery and the helix, by conveying the electricity from the one to the other. While the electricity flows through the helix, the magnet S N remains suspended within it, but falls down the moment 475it ceases. The magnet always turns its south pole S towards P, the positive wire of the battery, and its north pole towards the negative wire.
Note 225, p. 316. A copper wire coiled in the form represented in fig. 73 was the first and most simple form of the electro-dynamic cylinder. When its extremities P and n are connected with the positive and negative poles of a Voltaic battery, it becomes a perfect magnet during the time that a current of electricity is flowing through it, P and n being its north and south poles.
Note 226, p. 344. It is to Halley we are indebted for the first declination chart and the theory of 4 poles of maximum magnetic intensity, since confirmed by observation, as well as the earliest authentic values of the magnetic elements in London and St. Helena, where he went on purpose to make observations on terrestrial magnetism. Since that time M. Gauss has formed charts of the magnetic lines, and published a theory which very nearly represents the magnetic state of the globe. The mass of observations daily making by our cruizers and our Government surveys in every part of the earth is enormous.
Note 227, p. 360. In fig. 74 the hyperbola H P Y, the parabola p P R, and the ellipse A E P L, have the focal distance S P, and coincide through a small space on each side of the perihelion P; and, as a comet is only visible when near P, it is difficult to ascertain which of the three curves it moves in.
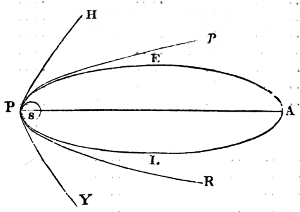
Fig. 74.
Note 228, p. 363. In fig. 75, E A represents the orbit of Halley’s comet, E T the orbit of the earth, and S the sun. The proportions are very nearly exact.
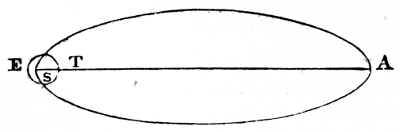
Fig. 75.
476Note 229, p. 382. Fig. 74 represents the curves in question. It is evident that, for the same focal distance S P, there can be but one circle and one parabola p P R, but that there may be an infinity of ellipses between the circle and the parabola, and an infinity of hyperbolas H P Y exterior to the parabola p P R.
Note 230, p. 387. Let A B, fig. 26, be the diameter of the earth’s orbit, and suppose a star to be seen in the direction A Sʹ from the earth when at A. Six months afterwards, the earth, having moved through half of its orbit, would arrive at B, and then the star would appear in the direction B Sʹ, if the diameter A B, as seen from Sʹ, had any sensible magnitude. But A B, which is 190,000,000 of miles, does not appear to be greater than the thickness of a spider’s thread, as seen from 61 Cygni, supposed to be the nearest of the fixed stars.
Note 231, p. 389. Stars whose parallax and proper motions are known.
| Name of Star. | Proper Motion. | Parallax. | Observers and Computers. |
|---|---|---|---|
| α Centauri | 3ʺ·764 | 0ʺ·92 | Maclear. |
| „ | .. | 1ʺ | Henderson. |
| 61 Cygni | 5ʺ·123 | 0ʺ·374 | Bessel. |
| α Lyræ | 0ʺ·364 | 0ʺ·207 | Peters. |
| Sirius | 1ʺ·234 | 0ʺ·230 | Henderson. |
| Arcturus | 2ʺ·269 | 0ʺ·127 | Peters. |
| Pole Star | 0ʺ·035 | 0ʺ·106 | Peters. |
| Capella | .. | 0ʺ·046 | Peters. |
| La Chevre | 0ʺ·461 | 0ʺ·046 | Peters. |
| ι Great Bear | 0ʺ·746 | 0ʺ·133 | Peters. |
The space run through in one second by these stars is therefore—
| α Centauri | 5 leagues | Henderson and Maclear. |
| 61 Cygni | 10 leagues | Bessel. |
| α Lyræ | 2 leagues | Struve and Peters. |
| Sirius | 6 leagues | Henderson and Maclear. |
| Arcturus | 22 leagues | Peters. |
| Pole Star | ½ league | Lindenau and Struve. |
| La Chevre | 12 leagues | Peters. |
| ι Great Bear | 7 leagues | Peters. |
There are three great discrepancies in the parallax of the star Argelander or 1830 Groombridge. M. Otto Struve makes it 0ʺ·034, which gives it a velocity of 251 leagues per second, while M. Faye finds the parallax to be between 0ʺ·03 and 0ʺ·01, which makes its velocity from 30 to 85 leagues per second.
These are all minimum velocities, because we can only determine on the celestial vault a projection perhaps much foreshortened of the real motions of the stars.
Note 232, pp. 398, 401. The following are the binary systems whose orbits have been accurately determined:—
| 477 | |||
| Name of Star. | Period in Years. | Perihelion Passage. | By whom Computed. |
|---|---|---|---|
| ζ Herculis | 30·216 | 1831·41 | Madler. |
| η Coronæ | 42·500 | 1807·21 | Madler. |
| ζ Cancri | 58·910 | 1853·37 | Madler. |
| ξ Ursæ Majoris | 58·262 | 1817·25 | Savary. |
| ω Leonis | 82·533 | 1849·76 | Villarceaux. |
| ρ Ophiuchi | 73·862 | 1806·83 | Encke. |
| 3062 in Dorpat Catalogue | 94·765 | 1837·41 | Madler. |
| ξ Bootis | 117·140 | 1779·88 | Sir J. Herschel. |
| δ Cygni | 178·700 | 1862·87 | Hind. |
| γ Virginis | 182·120 | 1836·43 | Sir J. Herschel. |
| Castor | 252·660 | 1855·83 | Sir J. Herschel. |
| ς Coronæ | 736·880 | 1826·48 | Hind. |
| γ Virginis | 632·270 | 1699 | Hind. |
| α Centauri | 77·000 | 1851·50 | Jacob. |
| Perihelion passage | 1836·40 |
| Inclination | 27° 36ʹ |
| Position of ascending Node | 19 7 |
| Angle between line of Nodes and Apsides | 295° 13 |
| Excentricity | 0·8794 |
| Period in years | 184·53 |
| Perihelion passage | 1830·56 |
| Inclination | 140° 39ʹ |
| Position of ascending Node | 217° 14ʹ |
| Angle between line of Nodes and Apsides | 266·53 |
| Eccentricity | 0·4381 |
| Period in years | 37·21 |
Note 233, p. 403. The mass is found in the manner explained in the text; but the method of computing the distance of the star may be made more clear by what follows. Though the orbit of the satellite star is really and apparently elliptical, let it be represented by C D O, fig. 14, for the sake of illustration, the earth being in d. It is clear that, when the star moves through C D O, its light will take longer in coming to the earth from O than from C, by the whole time it employs in passing through O C, the breadth of its orbit. When that time is known by observation, reduced to seconds, and multiplied by 190,000, which is the number of miles light darts through in a second, the product will be the breadth of the orbit in miles. From this the dimensions of the ellipse will be obtained by the aid of observation; the length and position of any diameter as S p may be found; and as all the angles of the triangle d S p can be determined by observation, the distance of the star from the earth may be computed.
Note 234, p. 405. The mean results of MM. Argelander, Otto Struve, and Luhndahl for stars in the northern hemisphere and the epoch 1790, places the point to which the sun is tending in 259° 5ʹ of right ascension and 55° 23ʹ of north polar distance. Mr. Gallaway computed from stars in the southern hemisphere, at the same epoch, the point to have been in 260° 1ʹ right ascension and 55° 37ʹ north polar distance, results nearly identical, though from very different data.
Note 235, p. 414. One of the globular clusters mentioned in the text is represented in fig. 1, plate 8. The stars are gradually condensed towards 478the centre, where they run together in a blaze. The more condensed part is projected on a ground of irregularly scattered stars, which fills the whole field of the telescope. There are few stars near this cluster.
Note 236, p. 420. Plate 8 shows five nebulæ as seen in Sir John Herschel’s 20-feet telescope.
1. An enormous ring seen obliquely with a dark centre and a small star at each extremity.
2. The ring in the constellation Lyra.
3. The dumb-bell nebula in Vulpicula.
4. The spiral nebula or brother system in the 20-feet telescope.
5. A spindle-shaped nebula.
Plate 9 represents some of the same objects as seen by Lord Rosse.
1. Nebula in the girdle of Andromeda.
2. The circular nebula of Lyra.
3. The dumb-bell nebula in Vulpicula.
The spiral nebulæ of 51 Messier, as seen by Lord Rosse, 1 in plate 10, represents fig. 4 of plate 8; and fig. 2 in the same plate is part of the great nebula in Orion, for the whole has never been seen, on account of extreme remoteness.
Note 237, pp. 32, 427. The motion of the earth is visibly proved by M. Foucault’s experiments. If a pendulum be left to oscillate quite freely, the forces producing the oscillations being in the vertical plane, there is no cause that can produce an absolute change in its position with regard to space; but the motion of the earth changes the position of a spectator with respect to the vertical plane, and he refers his own motion to it, which seems gradually to turn away from its position, precisely as a person in a boat refers his own motion to that of the land, and thus the motion of the earth is truly and visibly proved.
Plate 1.
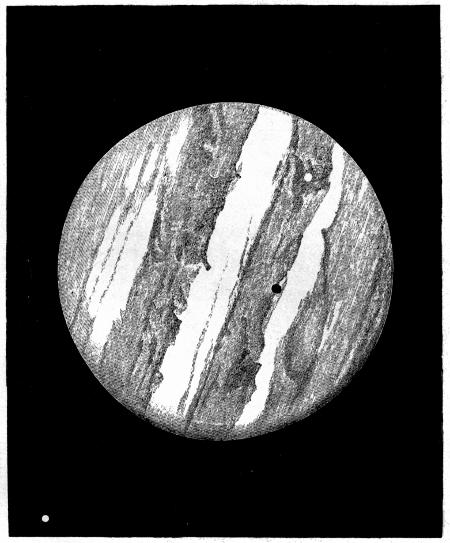
Plate 2.

Plate 3.

Plate 4.

Plate 5.

Plate 6.

Plate 7.
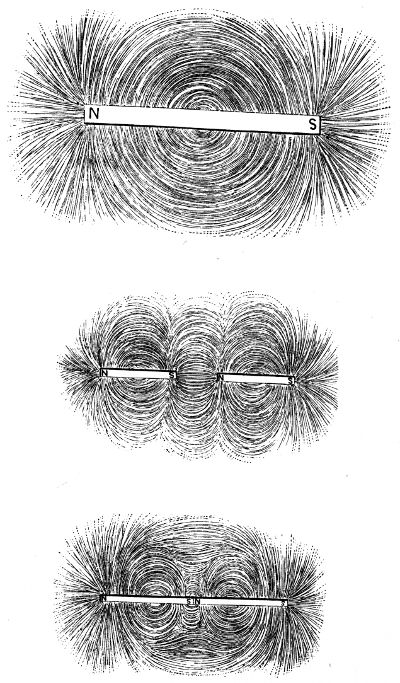
These correspond to No. 1, 6, and 7 of Faraday’s plate in his 29th Series of Experimental Researches in Electricity.
Plate 8.

Plate 9.
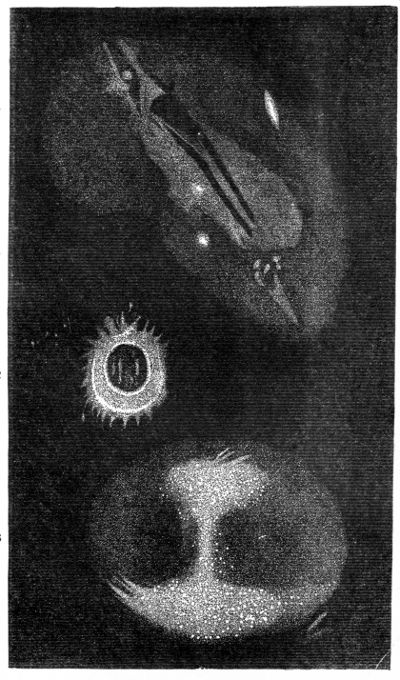
Plate 10.
Fig. 1.

Spiral nebulæ of 51 Messier, as seen by Lord Rosse.
Fig. 2.
Great nebula of Orion.
1. The mean distance of the earth from the sun is 95,000,000 miles, but to avoid the inconvenience of large numbers, it is assumed to be the unit of distance; hence the mean distance of Mars is 1·52369, or 1·5 nearly, that of the earth being = 1.
2. The obliquity given in the text is for the year 1858.
3. Sir John Herschel remarks that there are just as many thousands of feet in a degree of the meridian in our latitude as there are days in the year, viz. 365,000.
The Greenwich Observatory is in N. lat. 51° 28ʹ40ʺ.
4. Or more correctly 3422ʺ·325 and 238,793 miles, as deduced from Mr. Adams’ more accurate calculations.
5. Neptune was discovered in the year 1846.
6. The satellites of the two great planets on the farthest verge of the solar system form a singular exception to this law.
7. See the chapter on the Tides and Currents in the ‘Physical Geography,’ by the author, 4th edition.
8. Sir John Herschel on Meteorology.
9. Bakerian Lecture, by Michael Faraday, Esq. Phil. Trans. 1857.
11. M. Marbach of Breslau.
12. ‘Meteorology,’ by Sir J. Herschel.
13. This theory of heat and motion originated with Mr. Joule, of Manchester, who has maintained it with the greatest talent, both by experiment and analysis; and it has had an able advocate in Professor W. Thomson, of Glasgow.
14. To this remarkable man the world is indebted for the locomotive railway system, which is rapidly advancing the civilization of mankind. Britain may well be proud of its working classes, which can produce such men; and Mr. George Stephenson is not the only one; there are many others; but no man has ever had greater influence by his labours and discoveries on human affairs.
15. ‘Correlation of the Physical Forces, by W. R. Grove, Esq.,’ one of the most remarkable and talented works that has appeared, to which the author with pleasure acknowledges her obligations.
16. “Eripuit fulmen Cœlo, sceptrumque tyrannis,” is the inscription on a medal struck in honour of Franklin.
17. Faraday.
18. Professor Matteucci still expresses doubts on this subject, but has not yet finished his experiments.
19. Babbage.
20. Phil. Mag. for May 1858.
Some corrections were made to the original text. In particular, punctuation was corrected without further note. Inconsistent spelling and hyphenation was retained unless noted otherwise. There were two Notes 189 in the original; this was retained as printed. Spelling of Index entries was changed to reflect the body text where inconsistencies were found. Index page numbers were corrected where errors were found. Further corrections are noted below:
End of the Project Gutenberg EBook of On the Connexion of the Physical
Sciences, by Mary Somerville
*** END OF THIS PROJECT GUTENBERG EBOOK CONNEXION OF THE PHYSICAL SCIENCES ***
***** This file should be named 52869-h.htm or 52869-h.zip *****
This and all associated files of various formats will be found in:
http://www.gutenberg.org/5/2/8/6/52869/
Produced by Sonya Schermann and the Online Distributed
Proofreading Team at http://www.pgdp.net (This file was
produced from images generously made available by The
Internet Archive)
Updated editions will replace the previous one--the old editions
will be renamed.
Creating the works from public domain print editions means that no
one owns a United States copyright in these works, so the Foundation
(and you!) can copy and distribute it in the United States without
permission and without paying copyright royalties. Special rules,
set forth in the General Terms of Use part of this license, apply to
copying and distributing Project Gutenberg-tm electronic works to
protect the PROJECT GUTENBERG-tm concept and trademark. Project
Gutenberg is a registered trademark, and may not be used if you
charge for the eBooks, unless you receive specific permission. If you
do not charge anything for copies of this eBook, complying with the
rules is very easy. You may use this eBook for nearly any purpose
such as creation of derivative works, reports, performances and
research. They may be modified and printed and given away--you may do
practically ANYTHING with public domain eBooks. Redistribution is
subject to the trademark license, especially commercial
redistribution.
*** START: FULL LICENSE ***
THE FULL PROJECT GUTENBERG LICENSE
PLEASE READ THIS BEFORE YOU DISTRIBUTE OR USE THIS WORK
To protect the Project Gutenberg-tm mission of promoting the free
distribution of electronic works, by using or distributing this work
(or any other work associated in any way with the phrase "Project
Gutenberg"), you agree to comply with all the terms of the Full Project
Gutenberg-tm License (available with this file or online at
http://gutenberg.org/license).
Section 1. General Terms of Use and Redistributing Project Gutenberg-tm
electronic works
1.A. By reading or using any part of this Project Gutenberg-tm
electronic work, you indicate that you have read, understand, agree to
and accept all the terms of this license and intellectual property
(trademark/copyright) agreement. If you do not agree to abide by all
the terms of this agreement, you must cease using and return or destroy
all copies of Project Gutenberg-tm electronic works in your possession.
If you paid a fee for obtaining a copy of or access to a Project
Gutenberg-tm electronic work and you do not agree to be bound by the
terms of this agreement, you may obtain a refund from the person or
entity to whom you paid the fee as set forth in paragraph 1.E.8.
1.B. "Project Gutenberg" is a registered trademark. It may only be
used on or associated in any way with an electronic work by people who
agree to be bound by the terms of this agreement. There are a few
things that you can do with most Project Gutenberg-tm electronic works
even without complying with the full terms of this agreement. See
paragraph 1.C below. There are a lot of things you can do with Project
Gutenberg-tm electronic works if you follow the terms of this agreement
and help preserve free future access to Project Gutenberg-tm electronic
works. See paragraph 1.E below.
1.C. The Project Gutenberg Literary Archive Foundation ("the Foundation"
or PGLAF), owns a compilation copyright in the collection of Project
Gutenberg-tm electronic works. Nearly all the individual works in the
collection are in the public domain in the United States. If an
individual work is in the public domain in the United States and you are
located in the United States, we do not claim a right to prevent you from
copying, distributing, performing, displaying or creating derivative
works based on the work as long as all references to Project Gutenberg
are removed. Of course, we hope that you will support the Project
Gutenberg-tm mission of promoting free access to electronic works by
freely sharing Project Gutenberg-tm works in compliance with the terms of
this agreement for keeping the Project Gutenberg-tm name associated with
the work. You can easily comply with the terms of this agreement by
keeping this work in the same format with its attached full Project
Gutenberg-tm License when you share it without charge with others.
1.D. The copyright laws of the place where you are located also govern
what you can do with this work. Copyright laws in most countries are in
a constant state of change. If you are outside the United States, check
the laws of your country in addition to the terms of this agreement
before downloading, copying, displaying, performing, distributing or
creating derivative works based on this work or any other Project
Gutenberg-tm work. The Foundation makes no representations concerning
the copyright status of any work in any country outside the United
States.
1.E. Unless you have removed all references to Project Gutenberg:
1.E.1. The following sentence, with active links to, or other immediate
access to, the full Project Gutenberg-tm License must appear prominently
whenever any copy of a Project Gutenberg-tm work (any work on which the
phrase "Project Gutenberg" appears, or with which the phrase "Project
Gutenberg" is associated) is accessed, displayed, performed, viewed,
copied or distributed:
This eBook is for the use of anyone anywhere at no cost and with
almost no restrictions whatsoever. You may copy it, give it away or
re-use it under the terms of the Project Gutenberg License included
with this eBook or online at www.gutenberg.org/license
1.E.2. If an individual Project Gutenberg-tm electronic work is derived
from the public domain (does not contain a notice indicating that it is
posted with permission of the copyright holder), the work can be copied
and distributed to anyone in the United States without paying any fees
or charges. If you are redistributing or providing access to a work
with the phrase "Project Gutenberg" associated with or appearing on the
work, you must comply either with the requirements of paragraphs 1.E.1
through 1.E.7 or obtain permission for the use of the work and the
Project Gutenberg-tm trademark as set forth in paragraphs 1.E.8 or
1.E.9.
1.E.3. If an individual Project Gutenberg-tm electronic work is posted
with the permission of the copyright holder, your use and distribution
must comply with both paragraphs 1.E.1 through 1.E.7 and any additional
terms imposed by the copyright holder. Additional terms will be linked
to the Project Gutenberg-tm License for all works posted with the
permission of the copyright holder found at the beginning of this work.
1.E.4. Do not unlink or detach or remove the full Project Gutenberg-tm
License terms from this work, or any files containing a part of this
work or any other work associated with Project Gutenberg-tm.
1.E.5. Do not copy, display, perform, distribute or redistribute this
electronic work, or any part of this electronic work, without
prominently displaying the sentence set forth in paragraph 1.E.1 with
active links or immediate access to the full terms of the Project
Gutenberg-tm License.
1.E.6. You may convert to and distribute this work in any binary,
compressed, marked up, nonproprietary or proprietary form, including any
word processing or hypertext form. However, if you provide access to or
distribute copies of a Project Gutenberg-tm work in a format other than
"Plain Vanilla ASCII" or other format used in the official version
posted on the official Project Gutenberg-tm web site (www.gutenberg.org),
you must, at no additional cost, fee or expense to the user, provide a
copy, a means of exporting a copy, or a means of obtaining a copy upon
request, of the work in its original "Plain Vanilla ASCII" or other
form. Any alternate format must include the full Project Gutenberg-tm
License as specified in paragraph 1.E.1.
1.E.7. Do not charge a fee for access to, viewing, displaying,
performing, copying or distributing any Project Gutenberg-tm works
unless you comply with paragraph 1.E.8 or 1.E.9.
1.E.8. You may charge a reasonable fee for copies of or providing
access to or distributing Project Gutenberg-tm electronic works provided
that
- You pay a royalty fee of 20% of the gross profits you derive from
the use of Project Gutenberg-tm works calculated using the method
you already use to calculate your applicable taxes. The fee is
owed to the owner of the Project Gutenberg-tm trademark, but he
has agreed to donate royalties under this paragraph to the
Project Gutenberg Literary Archive Foundation. Royalty payments
must be paid within 60 days following each date on which you
prepare (or are legally required to prepare) your periodic tax
returns. Royalty payments should be clearly marked as such and
sent to the Project Gutenberg Literary Archive Foundation at the
address specified in Section 4, "Information about donations to
the Project Gutenberg Literary Archive Foundation."
- You provide a full refund of any money paid by a user who notifies
you in writing (or by e-mail) within 30 days of receipt that s/he
does not agree to the terms of the full Project Gutenberg-tm
License. You must require such a user to return or
destroy all copies of the works possessed in a physical medium
and discontinue all use of and all access to other copies of
Project Gutenberg-tm works.
- You provide, in accordance with paragraph 1.F.3, a full refund of any
money paid for a work or a replacement copy, if a defect in the
electronic work is discovered and reported to you within 90 days
of receipt of the work.
- You comply with all other terms of this agreement for free
distribution of Project Gutenberg-tm works.
1.E.9. If you wish to charge a fee or distribute a Project Gutenberg-tm
electronic work or group of works on different terms than are set
forth in this agreement, you must obtain permission in writing from
both the Project Gutenberg Literary Archive Foundation and Michael
Hart, the owner of the Project Gutenberg-tm trademark. Contact the
Foundation as set forth in Section 3 below.
1.F.
1.F.1. Project Gutenberg volunteers and employees expend considerable
effort to identify, do copyright research on, transcribe and proofread
public domain works in creating the Project Gutenberg-tm
collection. Despite these efforts, Project Gutenberg-tm electronic
works, and the medium on which they may be stored, may contain
"Defects," such as, but not limited to, incomplete, inaccurate or
corrupt data, transcription errors, a copyright or other intellectual
property infringement, a defective or damaged disk or other medium, a
computer virus, or computer codes that damage or cannot be read by
your equipment.
1.F.2. LIMITED WARRANTY, DISCLAIMER OF DAMAGES - Except for the "Right
of Replacement or Refund" described in paragraph 1.F.3, the Project
Gutenberg Literary Archive Foundation, the owner of the Project
Gutenberg-tm trademark, and any other party distributing a Project
Gutenberg-tm electronic work under this agreement, disclaim all
liability to you for damages, costs and expenses, including legal
fees. YOU AGREE THAT YOU HAVE NO REMEDIES FOR NEGLIGENCE, STRICT
LIABILITY, BREACH OF WARRANTY OR BREACH OF CONTRACT EXCEPT THOSE
PROVIDED IN PARAGRAPH 1.F.3. YOU AGREE THAT THE FOUNDATION, THE
TRADEMARK OWNER, AND ANY DISTRIBUTOR UNDER THIS AGREEMENT WILL NOT BE
LIABLE TO YOU FOR ACTUAL, DIRECT, INDIRECT, CONSEQUENTIAL, PUNITIVE OR
INCIDENTAL DAMAGES EVEN IF YOU GIVE NOTICE OF THE POSSIBILITY OF SUCH
DAMAGE.
1.F.3. LIMITED RIGHT OF REPLACEMENT OR REFUND - If you discover a
defect in this electronic work within 90 days of receiving it, you can
receive a refund of the money (if any) you paid for it by sending a
written explanation to the person you received the work from. If you
received the work on a physical medium, you must return the medium with
your written explanation. The person or entity that provided you with
the defective work may elect to provide a replacement copy in lieu of a
refund. If you received the work electronically, the person or entity
providing it to you may choose to give you a second opportunity to
receive the work electronically in lieu of a refund. If the second copy
is also defective, you may demand a refund in writing without further
opportunities to fix the problem.
1.F.4. Except for the limited right of replacement or refund set forth
in paragraph 1.F.3, this work is provided to you 'AS-IS' WITH NO OTHER
WARRANTIES OF ANY KIND, EXPRESS OR IMPLIED, INCLUDING BUT NOT LIMITED TO
WARRANTIES OF MERCHANTABILITY OR FITNESS FOR ANY PURPOSE.
1.F.5. Some states do not allow disclaimers of certain implied
warranties or the exclusion or limitation of certain types of damages.
If any disclaimer or limitation set forth in this agreement violates the
law of the state applicable to this agreement, the agreement shall be
interpreted to make the maximum disclaimer or limitation permitted by
the applicable state law. The invalidity or unenforceability of any
provision of this agreement shall not void the remaining provisions.
1.F.6. INDEMNITY - You agree to indemnify and hold the Foundation, the
trademark owner, any agent or employee of the Foundation, anyone
providing copies of Project Gutenberg-tm electronic works in accordance
with this agreement, and any volunteers associated with the production,
promotion and distribution of Project Gutenberg-tm electronic works,
harmless from all liability, costs and expenses, including legal fees,
that arise directly or indirectly from any of the following which you do
or cause to occur: (a) distribution of this or any Project Gutenberg-tm
work, (b) alteration, modification, or additions or deletions to any
Project Gutenberg-tm work, and (c) any Defect you cause.
Section 2. Information about the Mission of Project Gutenberg-tm
Project Gutenberg-tm is synonymous with the free distribution of
electronic works in formats readable by the widest variety of computers
including obsolete, old, middle-aged and new computers. It exists
because of the efforts of hundreds of volunteers and donations from
people in all walks of life.
Volunteers and financial support to provide volunteers with the
assistance they need, are critical to reaching Project Gutenberg-tm's
goals and ensuring that the Project Gutenberg-tm collection will
remain freely available for generations to come. In 2001, the Project
Gutenberg Literary Archive Foundation was created to provide a secure
and permanent future for Project Gutenberg-tm and future generations.
To learn more about the Project Gutenberg Literary Archive Foundation
and how your efforts and donations can help, see Sections 3 and 4
and the Foundation web page at http://www.pglaf.org.
Section 3. Information about the Project Gutenberg Literary Archive
Foundation
The Project Gutenberg Literary Archive Foundation is a non profit
501(c)(3) educational corporation organized under the laws of the
state of Mississippi and granted tax exempt status by the Internal
Revenue Service. The Foundation's EIN or federal tax identification
number is 64-6221541. Its 501(c)(3) letter is posted at
http://pglaf.org/fundraising. Contributions to the Project Gutenberg
Literary Archive Foundation are tax deductible to the full extent
permitted by U.S. federal laws and your state's laws.
The Foundation's principal office is located at 4557 Melan Dr. S.
Fairbanks, AK, 99712., but its volunteers and employees are scattered
throughout numerous locations. Its business office is located at
809 North 1500 West, Salt Lake City, UT 84116, (801) 596-1887, email
[email protected]. Email contact links and up to date contact
information can be found at the Foundation's web site and official
page at http://pglaf.org
For additional contact information:
Dr. Gregory B. Newby
Chief Executive and Director
[email protected]
Section 4. Information about Donations to the Project Gutenberg
Literary Archive Foundation
Project Gutenberg-tm depends upon and cannot survive without wide
spread public support and donations to carry out its mission of
increasing the number of public domain and licensed works that can be
freely distributed in machine readable form accessible by the widest
array of equipment including outdated equipment. Many small donations
($1 to $5,000) are particularly important to maintaining tax exempt
status with the IRS.
The Foundation is committed to complying with the laws regulating
charities and charitable donations in all 50 states of the United
States. Compliance requirements are not uniform and it takes a
considerable effort, much paperwork and many fees to meet and keep up
with these requirements. We do not solicit donations in locations
where we have not received written confirmation of compliance. To
SEND DONATIONS or determine the status of compliance for any
particular state visit http://pglaf.org
While we cannot and do not solicit contributions from states where we
have not met the solicitation requirements, we know of no prohibition
against accepting unsolicited donations from donors in such states who
approach us with offers to donate.
International donations are gratefully accepted, but we cannot make
any statements concerning tax treatment of donations received from
outside the United States. U.S. laws alone swamp our small staff.
Please check the Project Gutenberg Web pages for current donation
methods and addresses. Donations are accepted in a number of other
ways including checks, online payments and credit card donations.
To donate, please visit: http://pglaf.org/donate
Section 5. General Information About Project Gutenberg-tm electronic
works.
Professor Michael S. Hart is the originator of the Project Gutenberg-tm
concept of a library of electronic works that could be freely shared
with anyone. For thirty years, he produced and distributed Project
Gutenberg-tm eBooks with only a loose network of volunteer support.
Project Gutenberg-tm eBooks are often created from several printed
editions, all of which are confirmed as Public Domain in the U.S.
unless a copyright notice is included. Thus, we do not necessarily
keep eBooks in compliance with any particular paper edition.
Most people start at our Web site which has the main PG search facility:
http://www.gutenberg.org
This Web site includes information about Project Gutenberg-tm,
including how to make donations to the Project Gutenberg Literary
Archive Foundation, how to help produce our new eBooks, and how to
subscribe to our email newsletter to hear about new eBooks.