The Project Gutenberg eBook of On a Dynamical Top, by James Clerk Maxwell
This eBook is for the use of anyone anywhere in the United States and most other parts of the world at no cost and with almost no restrictions whatsoever. You may copy it, give it away or re-use it under the terms of the Project Gutenberg License included with this eBook or online at www.gutenberg.org. If you are not located in the United States, you will have to check the laws of the country where you are located before using this eBook.
Title: On a Dynamical Top
Author: James Clerk Maxwell
Release Date: June 1, 2002 [eBook #5192]
[Most recently updated: January 21, 2021]
Language: English
Character set encoding: UTF-8
Produced by: Gordon Keener
*** START OF THE PROJECT GUTENBERG EBOOK ON A DYNAMICAL TOP ***

On a Dynamical Top,

for exhibiting the phenomena of the motion of a system of invariable form about a fixed point, with some suggestions as to the Earth’s motion

James Clerk Maxwell

[From the Transactions of the Royal Society of Edinburgh, Vol. XXI. Part IV.]
(Read 20th April, 1857.)

To those who study the progress of exact science, the common spinning-top is a symbol of the labours and the perplexities of men who had successfully threaded the mazes of the planetary motions. The mathematicians of the last age, searching through nature for problems worthy of their analysis, found in this toy of their youth, ample occupation for their highest mathematical powers.

No illustration of astronomical precession can be devised more perfect than that presented by a properly balanced top, but yet the motion of rotation has intricacies far exceeding those of the theory of precession.

Accordingly, we find Euler and D’Alembert devoting their talent and their patience to the establishment of the laws of the rotation of solid bodies. Lagrange has incorporated his own analysis of the problem with his general treatment of mechanics, and since his time M. Poinsôt has brought the subject under the power of a more searching analysis than that of the calculus, in which ideas take the place of symbols, and intelligible propositions supersede equations.

In the practical department of the subject, we must notice the rotatory machine of Bohnenberger, and the nautical top of Troughton. In the first of these instruments we have the model of the Gyroscope, by which Foucault has been able to render visible the effects of the earth’s rotation. The beautiful experiments by which Mr J. Elliot has made the ideas of precession so familiar to us are performed with a top, similar in some respects to Troughton’s, though not borrowed from his.

The top which I have the honour to spin before the Society, differs from that of Mr Elliot in having more adjustments, and in being designed to exhibit far more complicated phenomena.

The arrangement of these adjustments, so as to produce the desired effects, depends on the mathematical theory of rotation. The method of exhibiting the motion of the axis of rotation, by means of a coloured disc, is essential to the success of these adjustments. This optical contrivance for rendering visible the nature of the rapid motion of the top, and the practical methods of applying the theory of rotation to such an instrument as the one before us, are the grounds on which I bring my instrument and experiments before the Society as my own.

I propose, therefore, in the first place, to give a brief outline of such parts of the theory of rotation as are necessary for the explanation of the phenomena of the top.

I shall then describe the instrument with its adjustments, and the effect of each, the mode of observing of the coloured disc when the top is in motion, and the use of the top in illustrating the mathematical theory, with the method of making the different experiments.

Lastly, I shall attempt to explain the nature of a possible variation in the earth’s axis due to its figure. This variation, if it exists, must cause a periodic inequality in the latitude of every place on the earth’s surface, going through its period in about eleven months. The amount of variation must be very small, but its character gives it importance, and the necessary observations are already made, and only require reduction.

On the Theory of Rotation.

The theory of the rotation of a rigid system is strictly deduced from the elementary laws of motion, but the complexity of the motion of the particles of a body freely rotating renders the subject so intricate, that it has never been thoroughly understood by any but the most expert mathematicians. Many who have mastered the lunar theory have come to erroneous conclusions on this subject; and even Newton has chosen to deduce the disturbance of the earth’s axis from his theory of the motion of the nodes of a free orbit, rather than attack the problem of the rotation of a solid body.

The method by which M. Poinsôt has rendered the theory more manageable, is by the liberal introduction of “appropriate ideas,” chiefly of a geometrical character, most of which had been rendered familiar to mathematicians by the writings of Monge, but which then first became illustrations of this branch of dynamics. If any further progress is to be made in simplifying and arranging the theory, it must be by the method which Poinsôt has repeatedly pointed out as the only one which can lead to a true knowledge of the subject,--that of proceeding from one distinct idea to another instead of trusting to symbols and equations.

An important contribution to our stock of appropriate ideas and methods has lately been made by Mr R. B. Hayward, in a paper, “On a Direct Method of estimating Velocities, Accelerations, and all similar quantities, with respect to axes, moveable in any manner in Space.” (Trans. Cambridge Phil. Soc Vol. x. Part I.)

* In this communication I intend to confine myself to that part of the subject which the top is intended io illustrate, namely, the alteration of the position of the axis in a body rotating freely about its centre of gravity. I shall, therefore, deduce the theory as briefly as possible, from two considerations only,--the permanence of the original angular momentum in direction and magnitude, and the permanence of the original vis viva.

* The mathematical difficulties of the theory of rotation arise chiefly from the want of geometrical illustrations and sensible images, by which we might fix the results of analysis in our minds.

It is easy to understand the motion of a body revolving about a fixed axle. Every point in the body describes a circle about the axis, and returns to its original position after each complete revolution. But if the axle itself be in motion, the paths of the different points of the body will no longer be circular or re-entrant. Even the velocity of rotation about the axis requires a careful definition, and the proposition that, in all motion about a fixed point, there is always one line of particles forming an instantaneous axis, is usually given in the form of a very repulsive mass of calculation. Most of these difficulties may be got rid of by devoting a little attention to the mechanics and geometry of the problem before entering on the discussion of the equations.

Mr Hayward, in his paper already referred to, has made great use of the mechanical conception of Angular Momentum.

Definition 1 The Angular Momentum of a particle about an axis is measured by the product of the mass of the particle, its velocity resolved in the normal plane, and the perpendicular from the axis on the direction of motion.

* The angular momentum of any system about an axis is the algebraical sum of the angular momenta of its parts.

As the rate of change of the linear momentum of a particle measures the moving force which acts on it, so the rate of change of angular momentum measures the moment of that force about an axis.

All actions between the parts of a system, being pairs of equal and opposite forces, produce equal and opposite changes in the angular momentum of those parts. Hence the whole angular momentum of the system is not affected by these actions and re-actions.

* When a system of invariable form revolves about an axis, the angular velocity of every part is the same, and the angular momentum about the axis is the product of the angular velocity and the moment of inertia about that axis.

* It is only in particular cases, however, that the whole angular momentum can be estimated in this way. In general, the axis of angular momentum differs from the axis of rotation, so that there will be a residual angular momentum about an axis perpendicular to that of rotation, unless that axis has one of three positions, called the principal axes of the body.

By referring everything to these three axes, the theory is greatly simplified. The moment of inertia about one of these axes is greater than that about any other axis through the same point, and that about one of the others is a minimum. These two are at right angles, and the third axis is perpendicular to their plane, and is called the mean axis.

* Let $A$, $B$, $C$ be the moments of inertia about the principal axes through the centre of gravity, taken in order of magnitude, and let $\omega_1$ $\omega_2$ $\omega_3$ be the angular velocities about them, then the angular momenta will be $A\omega_1$, $B\omega_2$, and $C\omega_3$.

Angular momenta may be compounded like forces or velocities, by the law of the “parallelogram,” and since these three are at right angles to each other, their resultant is

\begin{displaymath} \sqrt{A^2\omega_1^2 + B^2\omega_2^2 + C^2\omega_3^2} = H \end{displaymath} (1)

and this must be constant, both in magnitude and direction in space, since no external forces act on the body.

We shall call this axis of angular momentum the invariable axis. It is perpendicular to what has been called the invariable plane. Poinsôt calls it the axis of the couple of impulsion. The direction-cosines of this axis in the body are,


\begin{displaymath} \begin{array}{c c c} \displaystyle l = \frac{A\omega_1}{H}, ... ...ga_2}{H}, & \displaystyle n = \frac{C\omega_3}{H}. \end{array}\end{displaymath}

Since $I$, $m$ and $n$ vary during the motion, we need some additional condition to determine the relation between them. We find this in the property of the vis viva of a system of invariable form in which there is no friction. The vis viva of such a system must be constant. We express this in the equation


\begin{displaymath} A\omega_1^2 + B\omega_2^2 + C\omega_3^2 = V \end{displaymath} (2)

Substituting the values of $\omega_1$, $\omega_2$, $\omega_3$ in terms of $l$, $m$, $n$,


\begin{displaymath} \frac{l^2}{A} + \frac{m^2}{B} + \frac{n^2}{C} = \frac{V}{H^2}. \end{displaymath}

Let $1/A = a^2$, $1/B = b^2$, $1/c = c^2$, $V/H^2 = e^2$, and this equation becomes

\begin{displaymath} a^2l^2 + b^2m^2 + c^2n^2 = e^2 \end{displaymath} (3)

and the equation to the cone, described by the invariable axis within the body, is


\begin{displaymath} (a^2 - e^2) x^2 + (b^2 - e^2) y^2 + (c^2 - e^2) z^2 = 0 \end{displaymath} (4)

The intersections of this cone with planes perpendicular to the principal axes are found by putting $x$, $y$, or $z$, constant in this equation. By giving $e$ various values, all the different paths of the pole of the invariable axis, corresponding to different initial circumstances, may be traced.

Figure:
Figure 1

* In the figures, I have supposed $a^2 = 100$, $b^2= 107$, and $c^2= 110$. The first figure represents a section of the various cones by a plane perpendicular to the axis of $x$, which is that of greatest moment of inertia. These sections are ellipses having their major axis parallel to the axis of $b$. The value of $e^2$ corresponding to each of these curves is indicated by figures beside the curve. The ellipticity increases with the size of the ellipse, so that the section corresponding to $e^2 = 107$ would be two parallel straight lines (beyond the bounds of the figure), after which the sections would be hyperbolas.

Figure:
Figure 2

* The second figure represents the sections made by a plane, perpendicular to the mean axis. They are all hyperbolas, except when $e^2 = 107$, when the section is two intersecting straight lines.

Figure:
Figure 3

The third figure shows the sections perpendicular to the axis of least moment of inertia. From $e^2 = 110$ to $e^2 = 107$ the sections are ellipses, $e^2 = 107$ gives two parallel straight lines, and beyond these the curves are hyperbolas.

Figure:
Figure 4

* The fourth and fifth figures show the sections of the series of cones made by a cube and a sphere respectively. The use of these figures is to exhibit the connexion between the different curves described about the three principal axes by the invariable axis during the motion of the body.

Figure:
Figure 5

* We have next to compare the velocity of the invariable axis with respect to the body, with that of the body itself round one of the principal axes. Since the invariable axis is fixed in space, its motion relative to the body must be equal and opposite to that of the portion of the body through which it passes. Now the angular velocity of a portion of the body whose direction-cosines are $l$, $m$, $n$, about the axis of $x$ is


\begin{displaymath} \frac{\omega_1}{1 - l^2} - \frac{l}{1 - l^2}(l\omega_1 + m\omega_2 + n\omega-3). \end{displaymath}

Substituting the values of $\omega_1$, $\omega_2$, $\omega_3$, in terms of $l$, $m$, $n$, and taking account of equation (3), this expression becomes


\begin{displaymath} H\frac{(a^2 - e^2)}{1 - l^2}l. \end{displaymath}

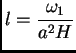Changing the sign and putting $\displaystyle l = \frac{\omega_1}{a^2H}$ we have the angular velocity of the invariable axis about that of $x$

\begin{displaymath} = \frac{\omega_1}{1 - l^2} \frac{e^2 - a^2}{a^2}, \end{displaymath}

always positive about the axis of greatest moment, negative about that of least moment, and positive or negative about the mean axis according to the value of $e^2$. The direction of the motion in every case is represented by the arrows in the figures. The arrows on the outside of each figure indicate the direction of rotation of the body.

* If we attend to the curve described by the pole of the invariable axis on the sphere in fig. 5, we shall see that the areas described by that point, if projected on the plane of $yz$, are swept out at the rate


\begin{displaymath} \omega_1 \frac{e^2 - a^2}{a^2}. \end{displaymath}

Now the semi-axes of the projection of the spherical ellipse described by the pole are


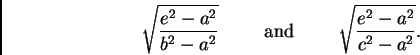
\begin{displaymath} \sqrt{\frac{e^2 - a^2}{b^2 - a^2}} \hspace{1cm}\textrm{and}\hspace{1cm} \sqrt{\frac{e^2 - a^2}{c^2 - a^2}}. \end{displaymath}

Dividing the area of this ellipse by the area described during one revolution of the body, we find the number of revolutions of the body during the description of the ellipse--


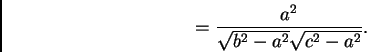
\begin{displaymath} = \frac{a^2}{\sqrt{b^2 - a^2}\sqrt{c^2 - a^2}}. \end{displaymath}

The projections of the spherical ellipses upon the plane of $yz$ are all similar ellipses, and described in the same number of revolutions; and in each ellipse so projected, the area described in any time is proportional to the number of revolutions of the body about the axis of $x$, so that if we measure time by revolutions of the body, the motion of the projection of the pole of the invariable axis is identical with that of a body acted on by an attractive central force varying directly as the distance. In the case of the hyperbolas in the plane of the greatest and least axis, this force must be supposed repulsive. The dots in the figures 1, 2, 3, are intended to indicate roughly the progress made by the invariable axis during each revolution of the body about the axis of $x$, $y$ and $z$ respectively. It must be remembered that the rotation about these axes varies with their inclination to the invariable axis, so that the angular velocity diminishes as the inclination increases, and therefore the areas in the ellipses above mentioned are not described with uniform velocity in absolute time, but are less rapidly swept out at the extremities of the major axis than at those of the minor.

* When two of the axes have equal moments of inertia, or $b = c$, then the angular velocity $\omega_1$ is constant, and the path of the invariable axis is circular, the number of revolutions of the body during one circuit of the invariable axis, being


\begin{displaymath} \frac{a^2}{b^2 - a^2} \end{displaymath}

The motion is in the same direction as that of the rotation, or in the opposite direction, according as the axis of $x$ is that of greatest or of least moment of inertia.

* Both in this case, and in that in which the three axes are unequal, the motion of the invariable axis in the body may be rendered very slow by diminishing the difference of the moments of inertia. The angular velocity of the axis of $x$ about the invariable axis in space is

\begin{displaymath} \omega_1\frac{e^2 - a^2l^2}{a^2(1 - l^2)}, \end{displaymath}

which is greater or less than $\omega_1$, as $e^2$ is greater or less than $a^2$, and, when these quantities are nearly equal, is very nearly the same as $\omega_1$ itself. This quantity indicates the rate of revolution of the axle of the top about its mean position, and is very easily observed.

* The instantaneous axis is not so easily observed. It revolves round the invariable axis in the same time with the axis of $x$, at a distance which is very small in the case when $a$, $b$, $c$, are nearly equal. From its rapid angular motion in space, and its near coincidence with the invariable axis, there is no advantage in studying its motion in the top.

* By making the moments of inertia very unequal, and in definite proportion to each other, and by drawing a few strong lines as diameters of the disc, the combination of motions will produce an appearance of epicycloids, which are the result of the continued intersection of the successive positions of these lines, and the cusps of the epicycloids lie in the curve in which the instantaneous axis travels. Some of the figures produced in this way are very pleasing.

In order to illustrate the theory of rotation experimentally, we must have a body balanced on its centre of gravity, and capable of having its principal axes and moments of inertia altered in form and position within certain limits. We must be able to make the axle of the instrument the greatest, least, or mean principal axis, or to make it not a principal axis at all, and we must be able to see the position of the invariable axis of rotation at any time. There must be three adjustments to regulate the position of the centre of gravity, three for the magnitudes of the moments of inertia, and three for the directions of the principal axes, nine independent adjustments, which may be distributed as we please among the screws of the instrument.

Figure:
Figure 6

The form of the body of the instrument which I have found most suitable is that of a bell (fig. 6). $C$ is a hollow cone of brass, $R$ is a heavy ring cast in the same piece. Six screws, with heavy heads, $x$, $y$, $z$, $x'$, $y'$, $z'$, work horizontally in the ring, and three similar screws, $l$, $m$, $n$, work vertically through the ring at equal intervals. $AS$ is the axle of the instrument, $SS$ is a brass screw working in the upper part of the cone $C$, and capable of being firmly clamped by means of the nut $c$. $B$ is a cylindrical brass bob, which may be screwed up or down the axis, and fixed in its place by the nut $b$.

The lower extremity of the axle is a fine steel point, finished without emery, and afterwards hardened. It runs in a little agate cup set in the top of the pillar $P$. If any emery had been embedded in the steel, the cup would soon be worn out. The upper end of the axle has also a steel point by which it may be kept steady while spinning.

When the instrument is in use, a coloured disc is attached to the upper end of the axle.

It will be seen that there are eleven adjustments, nine screws in the brass ring, the axle screwing in the cone, and the bob screwing on the axle. The advantage of the last two adjustments is, that by them large alterations can be made, which are not possible by means of the small screws.

The first thing to be done with the instrument is, to make the steel point at the end of the axle coincide with the centre of gravity of the whole. This is done roughly by screwing the axle to the right place nearly, and then balancing the instrument on its point, and screwing the bob and the horizontal screws till the instrument will remain balanced in any position in which it is placed.

When this adjustment is carefully made, the rotation of the top has no tendency to shake the steel point in the agate cup, however irregular the motion may appear to be.

The next thing to be done, is to make one of the principal axes of the central ellipsoid coincide with the axle of the top.

To effect this, we must begin by spinning the top gently about its axle, steadying the upper part with the finger at first. If the axle is already a principal axis the top will continue to revolve about its axle when the finger is removed. If it is not, we observe that the top begins to spin about some other axis, and the axle moves away from the centre of motion and then back to it again, and so on, alternately widening its circles and contracting them.

It is impossible to observe this motion successfully, without the aid of the coloured disc placed near the upper end of the axis. This disc is divided into sectors, and strongly coloured, so that each sector may be recognised by its colour when in rapid motion. If the axis about which the top is really revolving, falls within this disc, its position may be ascertained by the colour of the spot at the centre of motion. If the central spot appears red, we know that the invariable axis at that instant passes through the red part of the disc.

In this way we can trace the motion of the invariable axis in the revolving body, and we find that the path which it describes upon the disc may be a circle, an ellipse, an hyperbola, or a straight line, according to the arrangement of the instrument.

In the case in which the invariable axis coincides at first with the axle of the top, and returns to it after separating from it for a time, its true path is a circle or an ellipse having the axle in its circumference. The true principal axis is at the centre of the closed curve. It must be made to coincide with the axle by adjusting the vertical screws $l$, $m$, $n$.

Suppose that the colour of the centre of motion, when farthest from the axle, indicated that the axis of rotation passed through the sector $L$, then the principal axis must also lie in that sector at half the distance from the axle.

If this principal axis be that of greatest moment of inertia, we must raise the screw $l$ in order to bring it nearer the axle $A$. If it be the axis of least moment we must lower the screw $l$. In this way we may make the principal axis coincide with the axle. Let us suppose that the principal axis is that of greatest moment of inertia, and that we have made it coincide with the axle of the instrument. Let us also suppose that the moments of inertia about the other axes are equal, and very little less than that about the axle. Let the top be spun about the axle and then receive a disturbance which causes it to spin about some other axis. The instantaneous axis will not remain at rest either in space or in the body. In space it will describe a right cone, completing a revolution in somewhat less than the time of revolution of the top. In the body it will describe another cone of larger angle in a period which is longer as the difference of axes of the body is smaller. The invariable axis will be fixed in space, and describe a cone in the body.

The relation of the different motions may be understood from the following illustration. Take a hoop and make it revolve about a stick which remains at rest and touches the inside of the hoop. The section of the stick represents the path of the instantaneous axis in space, the hoop that of the same axis in the body, and the axis of the stick the invariable axis. The point of contact represents the pole of the instantaneous axis itself, travelling many times round the stick before it gets once round the hoop. It is easy to see that the direction in which the hoop moves round the stick, so that if the top be spinning in the direction $L$, $M$, $N$, the colours will appear in the same order.

By screwing the bob B up the axle, the difference of the axes of inertia may be diminished, and the time of a complete revolution of the invariable axis in the body increased. By observing the number of revolutions of the top in a complete cycle of colours of the invariable axis, we may determine the ratio of the moments of inertia.

By screwing the bob up farther, we may make the axle the principal axis of least moment of inertia.

The motion of the instantaneous axis will then be that of the point of contact of the stick with the outside of the hoop rolling on it. The order of colours will be $N$, $M$, $L$, if the top be spinning in the direction $L$, $M$, $N$, and the more the bob is screwed up, the more rapidly will the colours change, till it ceases to be possible to make the observations correctly.

In calculating the dimensions of the parts of the instrument, it is necessary to provide for the exhibition of the instrument with its axle either the greatest or the least axis of inertia. The dimensions and weights of the parts of the top which I have found most suitable, are given in a note at the end of this paper.

Now let us make the axes of inertia in the plane of the ring unequal. We may do this by screwing the balance screws $x$ and $x^1$ farther from the axle without altering the centre of gravity.

Let us suppose the bob $B$ screwed up so as to make the axle the axis of least inertia. Then the mean axis is parallel to $xx^1$, and the greatest is at right angles to $xx^1$ in the horizontal plane. The path of the invariable axis on the disc is no longer a circle but an ellipse, concentric with the disc, and having its major axis parallel to the mean axis $xx^1$.

The smaller the difference between the moment of inertia about the axle and about the mean axis, the more eccentric the ellipse will be; and if, by screwing the bob down, the axle be made the mean axis, the path of the invariable axis will be no longer a closed curve, but an hyperbola, so that it will depart altogether from the neighbourhood of the axle. When the top is in this condition it must be spun gently, for it is very difficult to manage it when its motion gets more and more eccentric.

When the bob is screwed still farther down, the axle becomes the axis of greatest inertia, and $xx^1$ the least. The major axis of the ellipse described by the invariable axis will now be perpendicular to $xx^1$, and the farther the bob is screwed down, the eccentricity of the ellipse will diminish, and the velocity with which it is described will increase.

I have now described all the phenomena presented by a body revolving freely on its centre of gravity. If we wish to trace the motion of the invariable axis by means of the coloured sectors, we must make its motion very slow compared with that of the top. It is necessary, therefore, to make the moments of inertia about the principal axes very nearly equal, and in this case a very small change in the position of any part of the top will greatly derange the position of the principal axis. So that when the top is well adjusted, a single turn of one of the screws of the ring is sufficient to make the axle no longer a principal axis, and to set the true axis at a considerable inclination to the axle of the top.

All the adjustments must therefore be most carefully arranged, or we may have the whole apparatus deranged by some eccentricity of spinning. The method of making the principal axis coincide with the axle must be studied and practised, or the first attempt at spinning rapidly may end in the destruction of the top, if not the table on which it is spun.

On the Earth’s Motion

We must remember that these motions of a body about its centre of gravity, are not illustrations of the theory of the precession of the Equinoxes. Precession can be illustrated by the apparatus, but we must arrange it so that the force of gravity acts the part of the attraction of the sun and moon in producing a force tending to alter the axis of rotation. This is easily done by bringing the centre of gravity of the whole a little below the point on which it spins. The theory of such motions is far more easily comprehended than that which we have been investigating.

But the earth is a body whose principal axes are unequal, and from the phenomena of precession we can determine the ratio of the polar and equatorial axes of the “central ellipsoid;” and supposing the earth to have been set in motion about any axis except the principal axis, or to have had its original axis disturbed in any way, its subsequent motion would be that of the top when the bob is a little below the critical position.

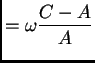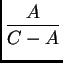The axis of angular momentum would have an invariable position in space, and would travel with respect to the earth round the axis of figure with a velocity $\displaystyle = \omega\frac{C - A}{A}$ where $\omega$ is the sidereal angular velocity of the earth. The apparent pole of the earth would travel (with respect to the earth) from west to east round the true pole, completing its circuit in $\displaystyle \frac{A}{C - A}$ sidereal days, which appears to be about 325.6 solar days.

The instantaneous axis would revolve about this axis in space in about a day, and would always be in a plane with the true axis of the earth and the axis of angular momentum. The effect of such a motion on the apparent position of a star would be, that its zenith distance should be increased and diminished during a period of 325.6 days. This alteration of zenith distance is the same above and below the pole, so that the polar distance of the star is unaltered. In fact the method of finding the pole of the heavens by observations of stars, gives the pole of the invariable axis, which is altered only by external forces, such as those of the sun and moon.

There is therefore no change in the apparent polar distance of stars due to this cause. It is the latitude which varies. The magnitude of this variation cannot be determined by theory. The periodic time of the variation may be found approximately from the known dynamical properties of the earth. The epoch of maximum latitude cannot be found except by observation, but it must be later in proportion to the east longitude of the observatory.

In order to determine the existence of such a variation of latitude, I have examined the observations of Polaris with the Greenwich Transit Circle in the years 1851-2-3-4. The observations of the upper transit during each month were collected, and the mean of each month found. The same was done for the lower transits. The difference of zenith distance of upper and lower transit is twice the polar distance of Polaris, and half the sum gives the co-latitude of Greenwich.

In this way I found the apparent co-latitude of Greenwich for each month of the four years specified.

There appeared a very slight indication of a maximum belonging to the set of months,

March, 51. Feb. 52. Dec. 52. Nov. 53. Sept. 54.

This result, however, is to be regarded as very doubtful, as there did not appear to be evidence for any variation exceeding half a second of space, and more observations would be required to establish the existence of so small a variation at all.

I therefore conclude that the earth has been for a long time revolving about an axis very near to the axis of figure, if not coinciding with it. The cause of this near coincidence is either the original softness of the earth, or the present fluidity of its interior. The axes of the earth are so nearly equal, that a considerable elevation of a tract of country might produce a deviation of the principal axis within the limits of observation, and the only cause which would restore the uniform motion, would be the action of a fluid which would gradually diminish the oscillations of latitude. The permanence of latitude essentially depends on the inequality of the earth’s axes, for if they had been all equal, any alteration of the crust of the earth would have produced new principal axes, and the axis of rotation would travel about those axes, altering the latitudes of all places, and yet not in the least altering the position of the axis of rotation among the stars.

Perhaps by a more extensive search and analysis of the observations of different observatories, the nature of the periodic variation of latitude, if it exist, may be determined. I am not aware of any calculations having been made to prove its non-existence, although, on dynamical grounds, we have every reason to look for some very small variation having the periodic time of 325.6 days nearly, a period which is clearly distinguished from any other astronomical cycle, and therefore easily recognised.

Note: Dimensions and Weights of the parts of the Dynamical Top.

Part Weight
  lb. oz.
I. Body of the top--
Mean diameter of ring, 4 inches.    
Section of ring, $\frac{1}{3}$ inch square.    
The conical portion rises from the upper and inner edge of the ring, a height of $1\frac{1}{2}$ inches from the base.    
The whole body of the top weighs 1 7
Each of the nine adjusting screws has its screw 1 inch long, and the screw and head together weigh 1 ounce. The whole weigh   9
II. Axle, &c.--
Length of axle 5 inches, of which $\frac{1}{2}$ inch at the bottom is occupied by the steel point, $3\frac{1}{2}$ inches are brass with a good screw turned on it, and the remaining inch is of steel, with a sharp point at the top. The whole weighs   $1\frac{1}{2}$
The bob $B$ has a diameter of 1.4 inches, and a thickness of .4. It weighs   $2\frac{3}{4}$
The nuts $b$ and $c$, for clamping the bob and the body of the top on the axle, each weigh $\frac{1}{2}$ oz.   1
Weight of whole top 2 $5\frac{1}{4}$

The best arrangement, for general observations, is to have the disc of card divided into four quadrants, coloured with vermilion, chrome yellow, emerald green, and ultramarine. These are bright colours, and, if the vermilion is good, they combine into a grayish tint when the rotation is about the axle, and burst into brilliant colours when the axis is disturbed. It is useful to have some concentric circles, drawn with ink, over the colours, and about 12 radii drawn in strong pencil lines. It is easy to distinguish the ink from the pencil lines, as they cross the invariable axis, by their want of lustre. In this way, the path of the invariable axis may be identified with great accuracy, and compared with theory.

* 7th May 1857. The paragraphs marked thus have been rewritten since the paper was read.

*** END OF THE PROJECT GUTENBERG EBOOK ON A DYNAMICAL TOP ***
This file should be named 5192-h.htm or 5192-h.zip
This and all associated files of various formats will be found in https://www.gutenberg.org/5/1/9/5192/
Updated editions will replace the previous one—the old editions will be renamed.
Creating the works from print editions not protected by U.S. copyright law means that no one owns a United States copyright in these works, so the Foundation (and you!) can copy and distribute it in the United States without permission and without paying copyright royalties. Special rules, set forth in the General Terms of Use part of this license, apply to copying and distributing Project Gutenberg™ electronic works to protect the PROJECT GUTENBERG™ concept and trademark. Project Gutenberg is a registered trademark, and may not be used if you charge for the eBooks, unless you receive specific permission. If you do not charge anything for copies of this eBook, complying with the rules is very easy. You may use this eBook for nearly any purpose such as creation of derivative works, reports, performances and research. They may be modified and printed and given away—you may do practically ANYTHING in the United States with eBooks not protected by U.S. copyright law. Redistribution is subject to the trademark license, especially commercial redistribution.
START: FULL LICENSE
THE FULL PROJECT GUTENBERG LICENSE
PLEASE READ THIS BEFORE YOU DISTRIBUTE OR USE THIS WORK
To protect the Project Gutenberg™ mission of promoting the free distribution of electronic works, by using or distributing this work (or any other work associated in any way with the phrase “Project Gutenberg”), you agree to comply with all the terms of the Full Project Gutenberg™ License available with this file or online at www.gutenberg.org/license.
Section 1. General Terms of Use and Redistributing Project Gutenberg™ electronic works
1.A. By reading or using any part of this Project Gutenberg™ electronic work, you indicate that you have read, understand, agree to and accept all the terms of this license and intellectual property (trademark/copyright) agreement. If you do not agree to abide by all the terms of this agreement, you must cease using and return or destroy all copies of Project Gutenberg™ electronic works in your possession. If you paid a fee for obtaining a copy of or access to a Project Gutenberg™ electronic work and you do not agree to be bound by the terms of this agreement, you may obtain a refund from the person or entity to whom you paid the fee as set forth in paragraph 1.E.8.
1.B. “Project Gutenberg” is a registered trademark. It may only be used on or associated in any way with an electronic work by people who agree to be bound by the terms of this agreement. There are a few things that you can do with most Project Gutenberg™ electronic works even without complying with the full terms of this agreement. See paragraph 1.C below. There are a lot of things you can do with Project Gutenberg™ electronic works if you follow the terms of this agreement and help preserve free future access to Project Gutenberg™ electronic works. See paragraph 1.E below.
1.C. The Project Gutenberg Literary Archive Foundation (“the Foundation” or PGLAF), owns a compilation copyright in the collection of Project Gutenberg™ electronic works. Nearly all the individual works in the collection are in the public domain in the United States. If an individual work is unprotected by copyright law in the United States and you are located in the United States, we do not claim a right to prevent you from copying, distributing, performing, displaying or creating derivative works based on the work as long as all references to Project Gutenberg are removed. Of course, we hope that you will support the Project Gutenberg™ mission of promoting free access to electronic works by freely sharing Project Gutenberg™ works in compliance with the terms of this agreement for keeping the Project Gutenberg™ name associated with the work. You can easily comply with the terms of this agreement by keeping this work in the same format with its attached full Project Gutenberg™ License when you share it without charge with others.
1.D. The copyright laws of the place where you are located also govern what you can do with this work. Copyright laws in most countries are in a constant state of change. If you are outside the United States, check the laws of your country in addition to the terms of this agreement before downloading, copying, displaying, performing, distributing or creating derivative works based on this work or any other Project Gutenberg™ work. The Foundation makes no representations concerning the copyright status of any work in any country outside the United States.
1.E. Unless you have removed all references to Project Gutenberg:
1.E.1. The following sentence, with active links to, or other immediate access to, the full Project Gutenberg™ License must appear prominently whenever any copy of a Project Gutenberg™ work (any work on which the phrase “Project Gutenberg” appears, or with which the phrase “Project Gutenberg” is associated) is accessed, displayed, performed, viewed, copied or distributed:
This eBook is for the use of anyone anywhere in the United States and most other parts of the world at no cost and with almost no restrictions whatsoever. You may copy it, give it away or re-use it under the terms of the Project Gutenberg License included with this eBook or online at www.gutenberg.org. If you are not located in the United States, you will have to check the laws of the country where you are located before using this eBook.
1.E.2. If an individual Project Gutenberg™ electronic work is derived from texts not protected by U.S. copyright law (does not contain a notice indicating that it is posted with permission of the copyright holder), the work can be copied and distributed to anyone in the United States without paying any fees or charges. If you are redistributing or providing access to a work with the phrase “Project Gutenberg” associated with or appearing on the work, you must comply either with the requirements of paragraphs 1.E.1 through 1.E.7 or obtain permission for the use of the work and the Project Gutenberg™ trademark as set forth in paragraphs 1.E.8 or 1.E.9.
1.E.3. If an individual Project Gutenberg™ electronic work is posted with the permission of the copyright holder, your use and distribution must comply with both paragraphs 1.E.1 through 1.E.7 and any additional terms imposed by the copyright holder. Additional terms will be linked to the Project Gutenberg™ License for all works posted with the permission of the copyright holder found at the beginning of this work.
1.E.4. Do not unlink or detach or remove the full Project Gutenberg™ License terms from this work, or any files containing a part of this work or any other work associated with Project Gutenberg™.
1.E.5. Do not copy, display, perform, distribute or redistribute this electronic work, or any part of this electronic work, without prominently displaying the sentence set forth in paragraph 1.E.1 with active links or immediate access to the full terms of the Project Gutenberg™ License.
1.E.6. You may convert to and distribute this work in any binary, compressed, marked up, nonproprietary or proprietary form, including any word processing or hypertext form. However, if you provide access to or distribute copies of a Project Gutenberg™ work in a format other than “Plain Vanilla ASCII” or other format used in the official version posted on the official Project Gutenberg™ web site (www.gutenberg.org), you must, at no additional cost, fee or expense to the user, provide a copy, a means of exporting a copy, or a means of obtaining a copy upon request, of the work in its original “Plain Vanilla ASCII” or other form. Any alternate format must include the full Project Gutenberg™ License as specified in paragraph 1.E.1.
1.E.7. Do not charge a fee for access to, viewing, displaying, performing, copying or distributing any Project Gutenberg™ works unless you comply with paragraph 1.E.8 or 1.E.9.
1.E.8. You may charge a reasonable fee for copies of or providing access to or distributing Project Gutenberg™ electronic works provided that
1.E.9. If you wish to charge a fee or distribute a Project Gutenberg™ electronic work or group of works on different terms than are set forth in this agreement, you must obtain permission in writing from both the Project Gutenberg Literary Archive Foundation and The Project Gutenberg Trademark LLC, the owner of the Project Gutenberg™ trademark. Contact the Foundation as set forth in Section 3 below.
1.F.
1.F.1. Project Gutenberg volunteers and employees expend considerable effort to identify, do copyright research on, transcribe and proofread works not protected by U.S. copyright law in creating the Project Gutenberg™ collection. Despite these efforts, Project Gutenberg™ electronic works, and the medium on which they may be stored, may contain “Defects,” such as, but not limited to, incomplete, inaccurate or corrupt data, transcription errors, a copyright or other intellectual property infringement, a defective or damaged disk or other medium, a computer virus, or computer codes that damage or cannot be read by your equipment.
1.F.2. LIMITED WARRANTY, DISCLAIMER OF DAMAGES - Except for the “Right of Replacement or Refund” described in paragraph 1.F.3, the Project Gutenberg Literary Archive Foundation, the owner of the Project Gutenberg™ trademark, and any other party distributing a Project Gutenberg™ electronic work under this agreement, disclaim all liability to you for damages, costs and expenses, including legal fees. YOU AGREE THAT YOU HAVE NO REMEDIES FOR NEGLIGENCE, STRICT LIABILITY, BREACH OF WARRANTY OR BREACH OF CONTRACT EXCEPT THOSE PROVIDED IN PARAGRAPH 1.F.3. YOU AGREE THAT THE FOUNDATION, THE TRADEMARK OWNER, AND ANY DISTRIBUTOR UNDER THIS AGREEMENT WILL NOT BE LIABLE TO YOU FOR ACTUAL, DIRECT, INDIRECT, CONSEQUENTIAL, PUNITIVE OR INCIDENTAL DAMAGES EVEN IF YOU GIVE NOTICE OF THE POSSIBILITY OF SUCH DAMAGE.
1.F.3. LIMITED RIGHT OF REPLACEMENT OR REFUND - If you discover a defect in this electronic work within 90 days of receiving it, you can receive a refund of the money (if any) you paid for it by sending a written explanation to the person you received the work from. If you received the work on a physical medium, you must return the medium with your written explanation. The person or entity that provided you with the defective work may elect to provide a replacement copy in lieu of a refund. If you received the work electronically, the person or entity providing it to you may choose to give you a second opportunity to receive the work electronically in lieu of a refund. If the second copy is also defective, you may demand a refund in writing without further opportunities to fix the problem.
1.F.4. Except for the limited right of replacement or refund set forth in paragraph 1.F.3, this work is provided to you ‘AS-IS’, WITH NO OTHER WARRANTIES OF ANY KIND, EXPRESS OR IMPLIED, INCLUDING BUT NOT LIMITED TO WARRANTIES OF MERCHANTABILITY OR FITNESS FOR ANY PURPOSE.
1.F.5. Some states do not allow disclaimers of certain implied warranties or the exclusion or limitation of certain types of damages. If any disclaimer or limitation set forth in this agreement violates the law of the state applicable to this agreement, the agreement shall be interpreted to make the maximum disclaimer or limitation permitted by the applicable state law. The invalidity or unenforceability of any provision of this agreement shall not void the remaining provisions.
1.F.6. INDEMNITY - You agree to indemnify and hold the Foundation, the trademark owner, any agent or employee of the Foundation, anyone providing copies of Project Gutenberg™ electronic works in accordance with this agreement, and any volunteers associated with the production, promotion and distribution of Project Gutenberg™ electronic works, harmless from all liability, costs and expenses, including legal fees, that arise directly or indirectly from any of the following which you do or cause to occur: (a) distribution of this or any Project Gutenberg™ work, (b) alteration, modification, or additions or deletions to any Project Gutenberg™ work, and (c) any Defect you cause.
Section 2. Information about the Mission of Project Gutenberg™
Project Gutenberg™ is synonymous with the free distribution of electronic works in formats readable by the widest variety of computers including obsolete, old, middle-aged and new computers. It exists because of the efforts of hundreds of volunteers and donations from people in all walks of life.
Volunteers and financial support to provide volunteers with the assistance they need are critical to reaching Project Gutenberg™’s goals and ensuring that the Project Gutenberg™ collection will remain freely available for generations to come. In 2001, the Project Gutenberg Literary Archive Foundation was created to provide a secure and permanent future for Project Gutenberg™ and future generations. To learn more about the Project Gutenberg Literary Archive Foundation and how your efforts and donations can help, see Sections 3 and 4 and the Foundation information page at www.gutenberg.org.
Section 3. Information about the Project Gutenberg Literary Archive Foundation
The Project Gutenberg Literary Archive Foundation is a non profit 501(c)(3) educational corporation organized under the laws of the state of Mississippi and granted tax exempt status by the Internal Revenue Service. The Foundation’s EIN or federal tax identification number is 64-6221541. Contributions to the Project Gutenberg Literary Archive Foundation are tax deductible to the full extent permitted by U.S. federal laws and your state’s laws.
The Foundation’s principal office is in Fairbanks, Alaska, with the mailing address: PO Box 750175, Fairbanks, AK 99775, but its volunteers and employees are scattered throughout numerous locations. Its business office is located at 809 North 1500 West, Salt Lake City, UT 84116, (801) 596-1887. Email contact links and up to date contact information can be found at the Foundation’s web site and official page at www.gutenberg.org/contact
For additional contact information:
Dr. Gregory B. Newby
Chief Executive and Director
[email protected]
Section 4. Information about Donations to the Project Gutenberg Literary Archive Foundation
Project Gutenberg™ depends upon and cannot survive without wide spread public support and donations to carry out its mission of increasing the number of public domain and licensed works that can be freely distributed in machine readable form accessible by the widest array of equipment including outdated equipment. Many small donations ($1 to $5,000) are particularly important to maintaining tax exempt status with the IRS.
The Foundation is committed to complying with the laws regulating charities and charitable donations in all 50 states of the United States. Compliance requirements are not uniform and it takes a considerable effort, much paperwork and many fees to meet and keep up with these requirements. We do not solicit donations in locations where we have not received written confirmation of compliance. To SEND DONATIONS or determine the status of compliance for any particular state visit www.gutenberg.org/donate.
While we cannot and do not solicit contributions from states where we have not met the solicitation requirements, we know of no prohibition against accepting unsolicited donations from donors in such states who approach us with offers to donate.
International donations are gratefully accepted, but we cannot make any statements concerning tax treatment of donations received from outside the United States. U.S. laws alone swamp our small staff.
Please check the Project Gutenberg Web pages for current donation methods and addresses. Donations are accepted in a number of other ways including checks, online payments and credit card donations. To donate, please visit: www.gutenberg.org/donate
Section 5. General Information About Project Gutenberg™ electronic works.
Professor Michael S. Hart was the originator of the Project Gutenberg™ concept of a library of electronic works that could be freely shared with anyone. For forty years, he produced and distributed Project Gutenberg™ eBooks with only a loose network of volunteer support.
Project Gutenberg™ eBooks are often created from several printed editions, all of which are confirmed as not protected by copyright in the U.S. unless a copyright notice is included. Thus, we do not necessarily keep eBooks in compliance with any particular paper edition.
Most people start at our Web site which has the main PG search facility: www.gutenberg.org.
This Web site includes information about Project Gutenberg™, including how to make donations to the Project Gutenberg Literary Archive Foundation, how to help produce our new eBooks, and how to subscribe to our email newsletter to hear about new eBooks.