

FOUR LECTURES DELIVERED AT PRINCETON UNIVERSITY, MAY, 1921
BY
WITH FOUR DIAGRAMS
PRINCETON
PRINCETON UNIVERSITY PRESS
1923
Copyright 1922 Princeton University Press Published 1922
NOTE.—The translation of these lectures into English was made by EDWIN PLIMPTON ADAMS, Professor of Physics in Princeton University
LECTURE I
SPACE AND TIME IN PRE-RELATIVITY PHYSICS
LECTURE II
THE THEORY OF SPECIAL RELATIVITY
LECTURE III
THE GENERAL THEORY OF RELATIVITY
LECTURE IV
THE GENERAL THEORY OF RELATIVITY (continued)
INDEX
THE theory of relativity is intimately connected with the theory of space and time. I shall therefore begin with a brief investigation of the origin of our ideas of space and time, although in doing so I know that I introduce a controversial subject. The object of all science, whether natural science or psychology, is to co-ordinate our experiences and to bring them into a logical system. How are our customary ideas of space and time related to the character of our experiences?
The experiences of an individual appear to us arranged in a series of events; in this series the single events which we remember appear to be ordered according to the criterion of "earlier" and "later," which cannot be analysed further. There exists, therefore, for the individual, an I-time, or subjective time. This in itself is not measurable. I can, indeed, associate numbers with the events, in such a way that a greater number is associated with the later event than with an earlier one; but the nature of this association may be quite arbitrary. This association I can define by means of a clock by comparing the order of events furnished by the clock with the order of the given series of events. We understand by a clock something which provides a series of events which can be counted, and which has other properties of which we shall speak later. [Pg 1]
By the aid of speech different individuals can, to a certain extent, compare their experiences. In this way it is shown that certain sense perceptions of different individuals correspond to each other, while for other sense perceptions no such correspondence can be established. We are accustomed to regard as real those sense perceptions which are common to different individuals, and which therefore are, in a measure, impersonal. The natural sciences, and in particular, the most fundamental of them, physics, deal with such sense perceptions. The conception of physical bodies, in particular of rigid bodies, is a relatively constant complex of such sense perceptions. A clock is also a body, or a system, in the same sense, with the additional property that the series of events which it counts is formed of elements all of which can be regarded as equal.
The only justification for our concepts and system of concepts is that they serve to represent the complex of our experiences; beyond this they have no legitimacy. I am convinced that the philosophers have had a harmful effect upon the progress of scientific thinking in removing certain fundamental concepts from the domain of empiricism, where they are under our control, to the intangible heights of the a priori. For even if it should appear that the universe of ideas cannot be deduced from experience by logical means, but is, in a sense, a creation of the human mind, without which no science is possible, nevertheless this universe of ideas is just as little independent of the nature of our experiences as clothes are of the form of the human body. This is particularly true of our concepts of time and space, which physicists have been obliged by the facts to bring down from the Olympus of the a priori in order to adjust them and put them in a serviceable condition. [Pg 2]
We now come to our concepts and judgments of space. It
is essential here also to pay strict attention to the relation of
experience to our concepts. It seems to me that Poincaré clearly
recognized the truth in the account he gave in his book, "La
Science et l'Hypothèse." Among all the changes which we can
perceive in a rigid body those are marked by their simplicity
which can be made reversibly by an arbitrary motion of the
body; Poincaré calls these, changes in position. By means of
simple changes in position we can bring two bodies into contact.
The theorems of congruence, fundamental in geometry, have to
do with the laws that govern such changes in position. For the
concept of space the following seems essential. We can form new
bodies by bringing bodies ,
, ... up to body
; we say that
we continue body
. We can continue body
in such a way that
it comes into contact with any other body,
. The ensemble of
all continuations of body
we can designate as the "space of
the body
." Then it is true that all bodies are in the "space of
the (arbitrarily chosen) body
." In this sense we cannot speak
of space in the abstract, but only of the "space belonging to a
body
." The earth's crust plays such a dominant rôle in our
daily life in judging the relative positions of bodies that it has
led to an abstract conception of space which certainly cannot be
defended. In order to free ourselves from this fatal error we shall
speak only of "bodies of reference," or "space of reference." It
was only through the theory of general relativity that refinement
of these concepts became necessary, as we shall see later.
I shall not go into detail concerning those properties of the
space of reference which lead to our conceiving points as elements
of space, and space as a continuum. Nor shall I attempt
to analyse further the properties of space which justify the conception
[Pg 3]
of continuous series of points, or lines. If these concepts
are assumed, together with their relation to the solid bodies of
experience, then it is easy to say what we mean by the three-dimensionality
of space; to each point three numbers, ,
,
(co-ordinates), may be associated, in such a way that this association
is uniquely reciprocal, and that
,
and
vary
continuously when the point describes a continuous series of points
(a line).
It is assumed in pre-relativity physics that the laws of the
orientation of ideal rigid bodies are consistent with Euclidean
geometry. What this means may be expressed as follows: Two
points marked on a rigid body form an interval. Such an interval
can be oriented at rest, relatively to our space of reference, in
a multiplicity of ways. If, now, the points of this space can
be referred to co-ordinates ,
,
, in such a way that the
differences of the co-ordinates,
,
,
, of the two ends
of the interval furnish the same sum of squares,
for every orientation of the interval, then the space of reference
is called Euclidean, and the co-ordinates Cartesian.[1] It is
sufficient, indeed, to make this assumption in the limit for an
infinitely small interval. Involved in this assumption there are
some which are rather less special, to which we must call attention
on account of their fundamental significance. In the first
place, it is assumed that one can move an ideal rigid body in an
arbitrary manner. In the second place, it is assumed that the behaviour
of ideal rigid bodies towards orientation is independent
[Pg 4]
of the material of the bodies and their changes of position, in the
sense that if two intervals can once be brought into coincidence,
they can always and everywhere be brought into coincidence.
Both of these assumptions, which are of fundamental importance
for geometry and especially for physical measurements,
naturally arise from experience; in the theory of general relativity
their validity needs to be assumed only for bodies and spaces
of reference which are infinitely small compared to astronomical
dimensions.
[1]This relation must hold for an arbitrary choice of the origin and of the
direction
(ratios )
of the interval.
The quantity we call the length of the interval. In order
that this may be uniquely determined it is necessary to fix arbitrarily
the length of a definite interval; for example, we can put
it equal to 1 (unit of length). Then the lengths of all other intervals
may be determined. If we make the
linearly dependent
upon a parameter
,
we obtain a line which has all the properties of the straight
lines of the Euclidean geometry. In particular, it easily follows
that by laying off
times the interval
upon a straight line, an
interval of length
is obtained. A length, therefore, means
the result of a measurement carried out along a straight line by
means of a unit measuring rod. It has a significance which is as
independent of the system of co-ordinates as that of a straight
line, as will appear in the sequel.
We come now to a train of thought which plays an analogous
role in the theories of special and general relativity. We ask
the question: besides the Cartesian co-ordinates which we have
used are there other equivalent co-ordinates? An interval has
[Pg 5]
a physical meaning which is independent of the choice of co-ordinates;
and so has the spherical surface which we obtain as
the locus of the end points of all equal intervals that we lay off
from an arbitrary point of our space of reference. If as well
as
(
from 1 to 3) are Cartesian co-ordinates of our space
of reference, then the spherical surface will be expressed in our
two systems of co-ordinates by the equations
How must the
be expressed in terms of the
in order that
equations (2) and (2a) may be equivalent to each other? Regarding
the
expressed as functions of the
, we can write,
by Taylor's theorem, for small values of the
,
If we substitute (2a) in this equation and compare with (1),
we see that the
must be linear functions of the
. If we
therefore put
[Pg 6]
then the equivalence of equations (2) and (2a) is expressed in
the form
It therefore follows that
must be a constant. If we put
= 1,
(2b) and (3a) furnish the conditions
in which
= 1, or
= 0, according
=
or
≠
. The
conditions (4) are called the conditions of orthogonality, and the
transformations (3), (4), linear orthogonal transformations. If
we stipulate that
shall be equal to the square of
the length in every system of co-ordinates, and if we always measure
with the same unit scale, then
must be equal to 1. Therefore
the linear orthogonal transformations are the only ones by
means of which we can pass from one Cartesian system of co-ordinates
in our space of reference to another. We see that in
applying such transformations the equations of a straight line
become equations of a straight line. Reversing equations (3a)
by multiplying both sides by
and summing for all
the
's, we obtain
The same coefficients,
, also determine the inverse substitution
of
. Geometrically,
is the cosine of the angle between
the
axis and the
axis.
[Pg 7]
To sum up, we can say that in the Euclidean geometry
there are (in a given space of reference) preferred systems of
co-ordinates, the Cartesian systems, which transform into each
other by linear orthogonal transformations. The distance between
two points of our space of reference, measured by a measuring
rod, is expressed in such co-ordinates in a particularly
simple manner. The whole of geometry may be founded upon
this conception of distance. In the present treatment, geometry
is related to actual things (rigid bodies), and its theorems are
statements concerning the behaviour of these things, which may
prove to be true or false.
One is ordinarily accustomed to study geometry divorced from any relation between its concepts and experience. There are advantages in isolating that which is purely logical and independent of what is, in principle, incomplete empiricism. This is satisfactory to the pure mathematician. He is satisfied if he can deduce his theorems from axioms correctly, that is, without errors of logic. The question as to whether Euclidean geometry is true or not does not concern him. But for our purpose it is necessary to associate the fundamental concepts of geometry with natural objects; without such an association geometry is worthless for the physicist. The physicist is concerned with the question as to whether the theorems of geometry are true or not. That Euclidean geometry, from this point of view, affirms something more than the mere deductions derived logically from definitions may be seen from the following simple consideration.
Between points of space there are
distances,
;
between these and the
co-ordinates we have the relations
[Pg 8]
From these equations the
co-ordinates may be
eliminated, and from this elimination at least
equations in the
, will result.[2]
Since the
are measurable
quantities, and by definition are independent of each other, these
relations between the
are not necessary a priori.
[2]In reality there are equations.
From the foregoing it is evident that the equations of transformation
(3), (4) have a fundamental significance in Euclidean
geometry, in that they govern the transformation from one
Cartesian system of co-ordinates to another. The Cartesian
systems of co-ordinates are characterized by the property that
in them the measurable distance between two points, , is
expressed by the equation
If and
are two Cartesian systems of co-ordinates,
then
The right-hand side is identically equal to the left-hand side
on account of the equations of the linear orthogonal transformation,
and the right-hand side differs from the left-hand side
only in that the are replaced by the
. This is expressed
by the statement that
is an invariant with respect to
linear orthogonal transformations. It is evident that in the Euclidean
geometry only such, and all such, quantities have an
objective significance, independent of the particular choice of
[Pg 9]
the Cartesian co-ordinates, as can be expressed by an invariant
with respect to linear orthogonal transformations. This is
the reason that the theory of invariants, which has to do with
the laws that govern the form of invariants, is so important for
analytical geometry.
As a second example of a geometrical invariant, consider a
volume. This is expressed by
By means of Jacobi's theorem we may write
where the integrand in the last integral is the functional determinant
of the
with respect to the
, and this by (3) is equal
to the determinant
of the coefficients of substitution,
. If
we form the determinant of the
from equation (4), we obtain,
by means of the theorem of multiplication of determinants,
If we limit ourselves to those transformations which have the determinant
+1,[3]
and only these arise from continuous variations
of the systems of co-ordinates, then
is an invariant.
[3]There are thus two kinds of Cartesian systems which are designated as "right-handed" and "left-handed" systems. The difference between these is familiar to every physicist and engineer. It is interesting to note that these two kinds of systems cannot be defined geometrically, but only the contrast between them.
[Pg 10]
Invariants, however, are not the only forms by means of
which we can give expression to the independence of the particular
choice of the Cartesian co-ordinates. Vectors and tensors
are other forms of expression. Let us express the fact that the
point with the current co-ordinates lies upon a straight line.
We have
Without limiting the generality we can put
If we multiply the equations by (compare (3a) and (5))
and sum for all the
's, we get
where we have written
These are the equations of straight lines with respect to a
second Cartesian system of co-ordinates '. They have the
same form as the equations with respect to the original system
of co-ordinates. It is therefore evident that straight lines
have a significance which is independent of the system of co-ordinates.
Formally, this depends upon the fact that the quantities (
) -
are
transformed as the components of
an interval,
. The ensemble of three quantities, defined for
every system of Cartesian co-ordinates, and which transform as
the components of an interval, is called a vector. If the three
[Pg 11]
components of a vector vanish for one system of Cartesian co-ordinates,
they vanish for all systems, because the equations of
transformation are homogeneous. We can thus get the meaning
of the concept of a vector without referring to a geometrical representation.
This behaviour of the equations of a straight line
can be expressed by saying that the equation of a straight line
is co-variant with respect to linear orthogonal transformations.
We shall now show briefly that there are geometrical entities
which lead to the concept of tensors. Let be the centre of a
surface of the second degree,
any point on the surface, and
the projections of the interval
upon the co-ordinate axes.
Then the equation of the surface is
In this, and in analogous cases, we shall omit the sign of summation,
and understand that the summation is to be carried out
for those indices that appear twice. We thus write the equation
of the surface
The quantities
determine the surface completely, for a given
position of the centre, with respect to the chosen system of
Cartesian co-ordinates. From the known law of transformation
for the
(3a) for linear orthogonal transformations, we easily
find the law of transformation for the
:[4]
[4]The equation
may, by (5), be replaced by
= 1,
from which the result stated immediately follows.
[Pg 12]
This transformation is homogeneous and of the first degree in
the . On account of this transformation, the
, are called
components of a tensor of the second rank (the latter on account
of the double index). If all the components,
, of a tensor with
respect to any system of Cartesian co-ordinates vanish, they
vanish with respect to every other Cartesian system. The form
and the position of the surface of the second degree is described
by this tensor (
).
Analytic tensors of higher rank (number of indices) may be
defined. It is possible and advantageous to regard vectors as
tensors of rank 1, and invariants (scalars) as tensors of rank 0.
In this respect, the problem of the theory of invariants may be so
formulated: according to what laws may new tensors be formed
from given tensors? We shall consider these laws now, in order
to be able to apply them later. We shall deal first only with the
properties of tensors with respect to the transformation from
one Cartesian system to another in the same space of reference,
by means of linear orthogonal transformations. As the laws are
wholly independent of the number of dimensions, we shall leave
this number, , indefinite at first.
Definition. If a figure is defined with respect to every system
of Cartesian co-ordinates in a space of reference of dimensions
by the
numbers
(
= number of indices), then
these numbers are the components of a tensor of rank
if the
transformation law is
[Pg 13]
Remark. From this definition it follows that
is an invariant, provided that (
), (
),
(
) ... are vectors.
Conversely, the tensor character of (
) may be inferred, if it
is known that the expression (8) leads to an invariant for an
arbitrary choice of the vectors (
), (
), etc.
Addition and Subtraction. By addition and subtraction of
the corresponding components of tensors of the same rank, a
tensor of equal rank results:
The proof follows from the definition of a tensor given above.
Multiplication. From a tensor of rank and a tensor of
rank
we may obtain a tensor of rank
+
by multiplying all
the components of the first tensor by all the components of the
second tensor:
Contraction. A tensor of rank - 2 may be obtained from
one of rank
by putting two definite indices equal to each other
and then summing for this single index:
[Pg 14]
The proof is
In addition to these elementary rules of operation there is
also the formation of tensors by differentiation ("erweiterung"):
New tensors, in respect to linear orthogonal transformations, may be formed from tensors according to these rules of operation.
Symmetrical Properties of Tensors. Tensors are called symmetrical
or skew-symmetrical in respect to two of their indices,
and
, if both the components which result from interchanging
the indices
and
are equal to each other or equal with
opposite signs.
Theorem. The character of symmetry or skew-symmetry exists independently of the choice of co-ordinates, and in this lies its importance. The proof follows from the equation defining tensors.
Special Tensors.
I. The quantities (4) are tensor components
(fundamental tensor).
[Pg 15]
Proof. If in the right-hand side of the equation of transformation
=
, we substitute
for
the quantities
(which are equal
to 1 or 0 according as
=
or
≠
),
we get
The justification for the last sign of equality becomes evident if
one applies (4) to the inverse substitution (5).
II. There is a tensor () skew-symmetrical with respect
to all pairs of indices, whose rank is equal to the number of
dimensions,
, and whose components are equal to +1 or -1
according as
is an even or odd permutation of 1 2 3....
The proof follows with the aid of the theorem proved above
These few simple theorems form the apparatus from the theory of invariants for building the equations of pre-relativity physics and the theory of special relativity.
We have seen that in pre-relativity physics, in order to specify
relations in space, a body of reference, or a space of reference,
is required, and, in addition, a Cartesian system of co-ordinates.
We can fuse both these concepts into a single one by thinking
of a Cartesian system of co-ordinates as a cubical frame-work
formed of rods each of unit length. The co-ordinates of the lattice
points of this frame are integral numbers. It follows from
the fundamental relation
that the members of such a space-lattice are all of unit length.
To specify relations in time, we require in addition a standard
clock placed at the origin of our Cartesian system of co-ordinates
[Pg 16]
or frame of reference. If an event takes place anywhere we can
assign to it three co-ordinates,
, and a time
, as soon as
we have specified the time of the clock at the origin which is
simultaneous with the event. We therefore give an objective significance
to the statement of the simultaneity of distant events,
while previously we have been concerned only with the simultaneity
of two experiences of an individual. The time so specified
is at all events independent of the position of the system of co-ordinates
in our space of reference, and is therefore an invariant
with respect to the transformation (3).
It is postulated that the system of equations expressing the laws of pre-relativity physics is co-variant with respect to the transformation (3), as are the relations of Euclidean geometry. The isotropy and homogeneity of space is expressed in this way.[5] We shall now consider some of the more important equations of physics from this point of view.
[5]The laws of physics could be expressed, even in case there were a unique direction in space, in such a way as to be co-variant with respect to the transformation (3); but such an expression would in this case be unsuitable. If there were a unique direction in space it would simplify the description of natural phenomena to orient the system of co-ordinates in a definite way in this direction. But if, on the other hand, there is no unique direction in space it is not logical to formulate the laws of nature in such a way as to conceal the equivalence of systems of co-ordinates that are oriented differently. We shall meet with this point of view again in the theories of special and general relativity.
The equations of motion of a material particle are
(
) is a vector;
, and therefore also
, an invariant; thus
[Pg 17]
(
) is a vector; in the same way it may be shown that
(
) is a vector. In general, the operation of differentiation
with respect to time does not alter the tensor character. Since
is an invariant (tensor of rank 0),
)
is a vector, or
tensor of rank 1 (by the theorem of the multiplication of tensors).
If the force (
) has a vector character, the same holds for
the difference (
. These equations of motion are
therefore valid in every other system of Cartesian co-ordinates
in the space of reference. In the case where the forces are conservative
we can easily recognize the vector character of (
).
For a potential energy,
, exists, which depends only upon the
mutual distances of the particles, and is therefore an invariant.
The vector character of the force,
=
,
is then a consequence of our general theorem about the derivative of a tensor
of rank 0.
Multiplying by the velocity, a tensor of rank 1, we obtain the
tensor equation
By contraction and multiplication by the scalar
we obtain the
equation of kinetic energy
[Pg 18]
If denotes the difference of the co-ordinates of the material
particle and a point fixed in space, then the
have the
character of vectors. We evidently have
=
, so that
the equations of motion of the particle may be written
Multiplying this equation by we obtain a tensor equation
Contracting the tensor on the left and taking the time average
we obtain the virial theorem, which we shall not consider
further. By interchanging the indices and subsequent subtraction,
we obtain, after a simple transformation, the theorem of
moments,
It is evident in this way that the moment of a vector is not a
vector but a tensor. On account of their skew-symmetrical character
there are not nine, but only three independent equations of
this system. The possibility of replacing skew-symmetrical tensors
of the second rank in space of three dimensions by vectors
depends upon the formation of the vector
[Pg 19]
If we multiply the skew-symmetrical tensor of rank 2 by the
special skew-symmetrical tensor introduced above, and contract
twice, a vector results whose components are numerically
equal to those of the tensor. These are the so-called axial vectors
which transform differently, from a right-handed system to
a left-handed system, from the
. There is a gain in
picturesqueness in regarding a skew-symmetrical tensor of rank 2
as a vector in space of three dimensions, but it does not represent
the exact nature of the corresponding quantity so well as
considering it a tensor.
We consider next the equations of motion of a continuous
medium. Let be the density,
the velocity components
considered as functions of the co-ordinates and the time,
the
volume forces per unit of mass, and
the stresses upon a
surface perpendicular to the a-axis in the direction of increasing
. Then the equations of motion are, by Newton's law,
in which
is the acceleration of the particle which
at time
has the co-ordinates
. If we express this acceleration
by partial differential coefficients, we obtain, after dividing by
,
We must show that this equation holds independently of the
special choice of the Cartesian system of co-ordinates. () is a
vector, and therefore
is also a vector.
[Pg 20]
is a tensor of rank 2,
is a tensor of rank 3. The second term on the left
results from contraction in the indices
,
. The vector character
of the second term on the right is obvious. In order that the first
term on the right may also be a vector it is necessary for
to be
a tensor. Then by differentiation and contraction
results,
and is therefore a vector, as it also is after multiplication by
the reciprocal scalar
. That
is a tensor, and therefore
transforms according to the equation
is proved in mechanics by integrating this equation over an infinitely
small tetrahedron. It is also proved there, by application
of the theorem of moments to an infinitely small parallelopipedon,
that
, and hence that the tensor of the stress is
a symmetrical tensor. From what has been said it follows that,
with the aid of the rules given above, the equation is co-variant
with respect to orthogonal transformations in space (rotational
transformations); and the rules according to which the quantities
in the equation must be transformed in order that the
equation may be co-variant also become evident.
The co-variance of the equation of continuity,
requires, from the foregoing, no particular discussion.
We shall also test for co-variance the equations which express
the dependence of the stress components upon the properties of
[Pg 21]
the matter, and set up these equations for the case of a compressible
viscous fluid with the aid of the conditions of co-variance.
If we neglect the viscosity, the pressure, , will be a scalar, and
will depend only upon the density and the temperature of the
fluid. The contribution to the stress tensor is then evidently
in which
is the special symmetrical tensor. This term will
also be present in the case of a viscous fluid. But in this case
there will also be pressure terms, which depend upon the space
derivatives of the
. We shall assume that this dependence is a
linear one. Since these terms must be symmetrical tensors, the
only ones which enter will be
(for
is a scalar). For
physical reasons (no slipping) it
is assumed that for symmetrical dilatations in all directions,
i.e. when
there are no frictional forces present, from which it follows that
=
. If only
is different from zero, let
,
by which
is determined. We then obtain for the complete
stress tensor,
[Pg 22]
The heuristic value of the theory of invariants, which arises from the isotropy of space (equivalence of all directions), becomes evident from this example.
We consider, finally, Maxwell's equations in the form which are the foundation of the electron theory of Lorentz.
is a vector, because the current density is defined as the
density of electricity multiplied by the vector velocity of the
electricity. According to the first three equations it is evident
that
is also to be regarded as a vector. Then
cannot be
regarded as a vector.[6] The equations may, however, easily be
[Pg 23]
interpreted if
is regarded as a skew-symmetrical tensor of the
second rank. In this sense, we write
,
,
in place of
,
,
respectively. Paying attention to the skew-symmetry
of
, the first three equations of (19) and (20) may be written
in the form
In contrast to
,
appears as a quantity which has the same type
of symmetry as an angular velocity. The divergence equations
then take the form
The last equation is a skew-symmetrical tensor equation of the
third rank (the skew-symmetry of the left-hand side with respect
to every pair of indices may easily be proved, if attention
is paid to the skew-symmetry of
). This notation is more
natural than the usual one, because, in contrast to the latter,
it is applicable to Cartesian left-handed systems as well as to
right-handed systems without change of sign.
[Pg 24]
[6]These considerations will make the reader familiar with tensor operations without the special difficulties of the four-dimensional treatment; corresponding considerations in the theory of special relativity (Minkowski's interpretation of the field) will then offer fewer difficulties.
THE previous considerations concerning the configuration of
rigid bodies have been founded, irrespective of the assumption
as to the validity of the Euclidean geometry, upon the hypothesis
that all directions in space, or all configurations of Cartesian systems
of co-ordinates, are physically equivalent. We may express
this as the "principle of relativity with respect to direction," and
it has been shown how equations (laws of nature) may be found,
in accord with this principle, by the aid of the calculus of tensors.
We now inquire whether there is a relativity with respect
to the state of motion of the space of reference; in other words,
whether there are spaces of reference in motion relatively to each
other which are physically equivalent. From the standpoint of
mechanics it appears that equivalent spaces of reference do exist.
For experiments upon the earth tell us nothing of the fact
that we are moving about the sun with a velocity of approximately
30 kilometres a second. On the other hand, this physical
equivalence does not seem to hold for spaces of reference in arbitrary
motion; for mechanical effects do not seem to be subject
to the same laws in a jolting railway train as in one moving with
uniform velocity; the rotation of the earth must be considered
in writing down the equations of motion relatively to the earth.
It appears, therefore, as if there were Cartesian systems of co-ordinates,
the so-called inertial systems, with reference to which
the laws of mechanics (more generally the laws of physics) are
expressed in the simplest form. We may infer the validity of
the following theorem: If is an inertial system, then every
[Pg 25]
other system
' which moves uniformly and without rotation
relatively to
, is also an inertial system; the laws of nature are
in concordance for all inertial systems. This statement we shall
call the "principle of special relativity." We shall draw certain
conclusions from this principle of "relativity of translation" just
as we have already done for relativity of direction.
In order to be able to do this, we must first solve the following
problem. If we are given the Cartesian co-ordinates, , and
the time,
, of an event relatively to one inertial system,
,
how can we calculate the co-ordinates,
, and the time,
', of
the same event relatively to an inertial system
' which moves
with uniform translation relatively to
? In the pre-relativity
physics this problem was solved by making unconsciously two
hypotheses:—
1. The time is absolute; the time of an event, ', relatively
to
' is the same as the time relatively to
. If instantaneous
signals could be sent to a distance, and if one knew that the
state of motion of a clock had no influence on its rate, then this
assumption would be physically established. For then clocks,
similar to one another, and regulated alike, could be distributed
over the systems
and
', at rest relatively to them, and their
indications would be independent of the state of motion of the
systems; the time of an event would then be given by the clock
in its immediate neighbourhood.
2. Length is absolute; if an interval, at rest relatively to ,
has a length
, then it has the same length
relatively to a
system
' which is in motion relatively to
.
If the axes of and
' are parallel to each other, a simple
calculation based on these two assumptions, gives the equations
[Pg 26]
of transformation
This transformation is known as the "Galilean Transformation."
Differentiating twice by the time, we get
Further, it follows that for two simultaneous events,
The invariance of the distance between the two points results
from squaring and adding. From this easily follows the co-variance
of Newton's equations of motion with respect to the
Galilean transformation (21). Hence it follows that classical
mechanics is in accord with the principle of special relativity if
the two hypotheses respecting scales and clocks are made.
But this attempt to found relativity of translation upon the
Galilean transformation fails when applied to electromagnetic
phenomena. The Maxwell-Lorentz electromagnetic equations
are not co-variant with respect to the Galilean transformation.
In particular, we note, by (21), that a ray of light which referred
to has a velocity
, has a different velocity referred to
',
depending upon its direction. The space of reference of
is
therefore distinguished, with respect to its physical properties,
from all spaces of reference which are in motion relatively to it
(quiescent æther). But all experiments have shown that electromagnetic
and optical phenomena, relatively to the earth as the
[Pg 27]
body of reference, are not influenced by the translational velocity
of the earth. The most important of these experiments are
those of Michelson and Morley, which I shall assume are known.
The validity of the principle of special relativity can therefore
hardly be doubted.
On the other hand, the Maxwell-Lorentz equations have
proved their validity in the treatment of optical problems in
moving bodies. No other theory has satisfactorily explained the
facts of aberration, the propagation of light in moving bodies
(Fizeau), and phenomena observed in double stars (De Sitter).
The consequence of the Maxwell-Lorentz equations that in a
vacuum light is propagated with the velocity , at least with respect
to a definite inertial system
, must therefore be regarded
as proved. According to the principle of special relativity, we
must also assume the truth of this principle for every other
inertial system.
Before we draw any conclusions from these two principles
we must first review the physical significance of the concepts
"time" and "velocity." It follows from what has gone before, that
co-ordinates with respect to an inertial system are physically
defined by means of measurements and constructions with the
aid of rigid bodies. In order to measure time, we have supposed
a clock, , present somewhere, at rest relatively to
. But
we cannot fix the time, by means of this clock, of an event
whose distance from the clock is not negligible; for there are no
"instantaneous signals" that we can use in order to compare the
time of the event with that of the clock. In order to complete the
definition of time we may employ the principle of the constancy
of the velocity of light in a vacuum. Let us suppose that we
place similar clocks at points of the system
, at rest relatively
[Pg 28]
to it, and regulated according to the following scheme. A ray
of light is sent out from one of the clocks,
, at the instant
when it indicates the time
, and travels through a vacuum a
distance
, to the clock
; at the instant when this ray meets
the clock
the latter is set to indicate the time
=
+
.[7]
The principle of the constancy of the velocity of light then states
that this adjustment of the clocks will not lead to contradictions.
With clocks so adjusted, we can assign the time to events which
take place near any one of them. It is essential to note that this
definition of time relates only to the inertial system
, since
we have used a system of clocks at rest relatively to
. The
assumption which was made in the pre-relativity physics of the
absolute character of time (i.e. the independence of time of the
choice of the inertial system) does not follow at all from this
definition.
[7]Strictly speaking, it would be more correct to define simultaneity first,
somewhat as follows: two events taking place at the points and
of
the system
are simultaneous if they appear at the same instant when
observed from the middle point,
, of the interval
. Time is then
defined as the ensemble of the indications of similar clocks, at rest relatively
to
, which register the same simultaneously.
The theory of relativity is often criticized for giving, without justification, a central theoretical role to the propagation of light, in that it founds the concept of time upon the law of propagation of light. The situation, however, is somewhat as follows. In order to give physical significance to the concept of time, processes of some kind are required which enable relations to be established between different places. It is immaterial what kind of processes one chooses for such a definition of time. It is advantageous, however, for the theory, to choose only those [Pg 29] processes concerning which we know something certain. This holds for the propagation of light in vacuo in a higher degree than for any other process which could be considered, thanks to the investigations of Maxwell and H. A. Lorentz.
From all of these considerations, space and time data have
a physically real, and not a mere fictitious, significance; in particular
this holds for all the relations in which co-ordinates and
time enter, e.g. the relations (21). There is, therefore, sense in
asking whether those equations are true or not, as well as in
asking what the true equations of transformation are by which
we pass from one inertial system to another,
', moving relatively
to it. It may be shown that this is uniquely settled by
means of the principle of the constancy of the velocity of light
and the principle of special relativity.
To this end we think of space and time physically defined
with respect to two inertial systems, and
', in the way that
has been shown. Further, let a ray of light pass from one point
to another point
of
through a vacuum. If
is the measured
distance between the two points, then the propagation of light
must satisfy the equation
If we square this equation, and express by the differences
of the co-ordinates,
, in place of this equation we can write
This equation formulates the principle of the constancy of the
velocity of light relatively to
. It must hold whatever may be
the motion of the source which emits the ray of light.
[Pg 30]
The same propagation of light may also be considered relatively
to ', in which case also the principle of the constancy of
the velocity of light must be satisfied. Therefore, with respect
to
', we have the equation
Equations (22a) and (22) must be mutually consistent with
each other with respect to the transformation which transforms
from to
'. A transformation which effects this we shall call
a "Lorentz transformation."
Before considering these transformations in detail we shall
make a few general remarks about space and time. In the pre-relativity
physics space and time were separate entities. Specifications
of time were independent of the choice of the space of
reference. The Newtonian mechanics was relative with respect
to the space of reference, so that, e.g. the statement that two
non-simultaneous events happened at the same place had no objective
meaning (that is, independent of the space of reference).
But this relativity had no role in building up the theory. One
spoke of points of space, as of instants of time, as if they were
absolute realities. It was not observed that the true element
of the space-time specification was the event, specified by the
four numbers ,
,
,
. The conception of something
happening was always that of a four-dimensional continuum; but
the recognition of this was obscured by the absolute character
of the pre-relativity time. Upon giving up the hypothesis of the
absolute character of time, particularly that of simultaneity, the
four-dimensionality of the time-space concept was immediately
recognized. It is neither the point in space, nor the instant in
[Pg 31]
time, at which something happens that has physical reality, but
only the event itself. There is no absolute (independent of the
space of reference) relation in space, and no absolute relation
in time between two events, but there is an absolute (independent
of the space of reference) relation in space and time, as
will appear in the sequel. The circumstance that there is no
objective rational division of the four-dimensional continuum
into a three-dimensional space and a one-dimensional time continuum
indicates that the laws of nature will assume a form
which is logically most satisfactory when expressed as laws in
the four-dimensional space-time continuum. Upon this depends
the great advance in method which the theory of relativity owes
to Minkowski. Considered from this standpoint, we must regard
,
,
,
as the four co-ordinates of an event in the
four-dimensional continuum. We have far less success in picturing
to ourselves relations in this four-dimensional continuum than
in the three-dimensional Euclidean continuum; but it must be
emphasized that even in the Euclidean three-dimensional geometry
its concepts and relations are only of an abstract nature in
our minds, and are not at all identical with the images we form
visually and through our sense of touch. The non-divisibility of
the four-dimensional continuum of events does not at all, however,
involve the equivalence of the space co-ordinates with the
time co-ordinate. On the contrary, we must remember that the
time co-ordinate is defined physically wholly differently from the
space co-ordinates. The relations (22) and (22a) which when
equated define the Lorentz transformation show, further, a difference
in the role of the time co-ordinate from that of the space
co-ordinates; for the term
has the opposite sign to the space
terms,
,
,
.
[Pg 32]
Before we analyse further the conditions which define the
Lorentz transformation, we shall introduce the light-time, ,
in place of the time,
, in order that the constant
shall not
enter explicitly into the formulas to be developed later. Then
the Lorentz transformation is defined in such a way that, first,
it makes the equation
a co-variant equation, that is, an equation which is satisfied with
respect to every inertial system if it is satisfied in the inertial
system to which we refer the two given events (emission and
reception of the ray of light). Finally, with Minkowski, we introduce
in place of the real time co-ordinate
, the imaginary
time co-ordinate
Then the equation defining the propagation of light, which must
be co-variant with respect to the Lorentz transformation, becomes
This condition is always satisfied[8] if we satisfy the more general
condition that
[Pg 33]
shall be an invariant with respect to the transformation. This
condition is satisfied only by linear transformations, that is,
transformations of the type
in which the summation over the
is to be extended from
= 1
to
= 4. A glance at equations (23) and (24) shows that the
Lorentz transformation so defined is identical with the translational
and rotational transformations of the Euclidean geometry,
if we disregard the number of dimensions and the relations of reality.
We can also conclude that the coefficients
must satisfy
the conditions
Since the ratios of the
are real, it follows that all the
and
the
are real, except
,
,
,
,
,
and
, which
are purely imaginary.
[8]That this specialization lies in the nature of the case will be evident later.
Special Lorentz Transformation. We obtain the simplest
transformations of the type of (24) and (25) if only two of the
co-ordinates are to be transformed, and if all the , which determine
the new origin, vanish. We obtain then for the indices
1 and 2, on account of the three independent conditions which
the relations (25) furnish,
[Pg 34]
This is a simple rotation in space of the (space) co-ordinate
system about -axis. We see that the rotational transformation
in space (without the time transformation) which we studied
before is contained in the Lorentz transformation as a special
case. For the indices 1 and 4 we obtain, in an analogous manner,
On account of the relations of reality must be taken as
imaginary. To interpret these equations physically, we introduce
the real light-time
and the velocity
of
' relatively to
,
instead of the imaginary angle
. We have, first,
Since for the origin of
' i.e., for
= 0, we must have
,
it follows from the first of these equations that
and also
[Pg 35]
so that we obtain
These equations form the well-known special Lorentz transformation,
which in the general theory represents a rotation,
through an imaginary angle, of the four-dimensional system of
co-ordinates. If we introduce the ordinary time , in place of the
light-time
, then in (29) we must replace
by
and
by
.
We must now fill in a gap. From the principle of the constancy
of the velocity of light it follows that the equation
has a significance which is independent of the choice of the inertial
system; but the invariance of the quantity
does
not at all follow from this. This quantity might be transformed
with a factor. This depends upon the fact that the right-hand
side of (29) might be multiplied by a factor
, independent of
.
But the principle of relativity does not permit this factor to be
different from 1, as we shall now show. Let us assume that we
have a rigid circular cylinder moving in the direction of its axis.
If its radius, measured at rest with a unit measuring rod is equal
to
, its radius
in motion, might be different from
, since
the theory of relativity does not make the assumption that the
shape of bodies with respect to a space of reference is independent
of their motion relatively to this space of reference. But
[Pg 36]
all directions in space must be equivalent to each other.
may
therefore depend upon the magnitude
of the velocity, but not
upon its direction;
must therefore be an even function of
. If
the cylinder is at rest relatively to
' the equation of its lateral
surface is
If we write the last two equations of (29) more generally
then the lateral surface of the cylinder referred to
satisfies the
equation
The factor
therefore measures the lateral contraction of the
cylinder, and can thus, from the above, be only an even function
of
.
If we introduce a third system of co-ordinates, ", which
moves relatively to ' with velocity
in the direction of the
negative
-axis of
, we obtain, by applying (29) twice,
Now, since
must be equal to
and since we assume
that we use the same measuring rods in all the systems, it follows
that the transformation of
" to must be the identical
[Pg 37]
transformation (since the possibility
does not need to
be considered). It is essential for these considerations to assume
that the behaviour of the measuring rods does not depend upon
the history of their previous motion.
Moving Measuring Rods and Clocks. At the definite -time,
, the position of the points given by the integers
, is with respect to
, given by
; this follows
from the first of equations (29) and expresses the Lorentz
contraction. A clock at rest at the origin
of
, whose
beats are characterized by
, will, when observed from
',
have beats characterized by
this follows from the second of equations (29) and shows that
the clock goes slower than if it were at rest relatively to
'.
These two consequences, which hold, mutatis mutandis, for every
system of reference, form the physical content, free from
convention, of the Lorentz transformation.
Addition Theorem for Velocities. If we combine two special
Lorentz transformations with the relative velocities and
,
then the velocity of the single Lorentz transformation which
takes the place of the two separate ones is, according to (27),
given by
[Pg 38]
General Statements about the Lorentz Transformation and
its Theory of Invariants. The whole theory of invariants of the
special theory of relativity depends upon the invariant (23).
Formally, it has the same rôle in the four-dimensional space-time
continuum as the invariant
+
+
in the Euclidean
geometry and in the pre-relativity physics. The latter quantity
is not an invariant with respect to all the Lorentz transformations;
the quantity
of equation (23) assumes the rôle of this
invariant. With respect to an arbitrary inertial system,
may
be determined by measurements; with a given unit of measure
it is a completely determinate quantity, associated with an arbitrary
pair of events.
The invariant differs, disregarding the number of dimensions,
from the corresponding invariant of the Euclidean geometry
in the following points. In the Euclidean geometry
is
necessarily positive; it vanishes only when the two points concerned
come together. On the other hand, from the vanishing
of
it cannot be concluded that the two space-time points fall together;
the vanishing of this quantity
, is the invariant condition
that the two space-time points can be connected by a light
signal in vacuo. If
a point (event) represented in the
four-dimensional space of the
,
,
,
then all the "points" which
can be connected to
by means of a light signal lie upon the
cone
= 0 (compare Fig. 1, in which the dimension
is suppressed).
The "upper" half of the cone may contain the "points"
to which light signals can be sent from
; then the "lower" half
[Pg 39]
of the cone will contain the "points" from which light signals
can be sent to
. The points
enclosed by the conical surface
furnish, with
, a negative
;
as well as
is then,
according to Minkowski, of the nature of a time. Such intervals
represent elements of possible paths of motion, the velocity being
less than that of light.[9] In
this case the
-axis may be drawn
[Pg 40]
in the direction of
by suitably choosing the state of motion
of the inertial system. If
lies outside of the "light-cone" then
is of the nature of a space; in this case, by properly choosing
the inertial system,
can be made to vanish.
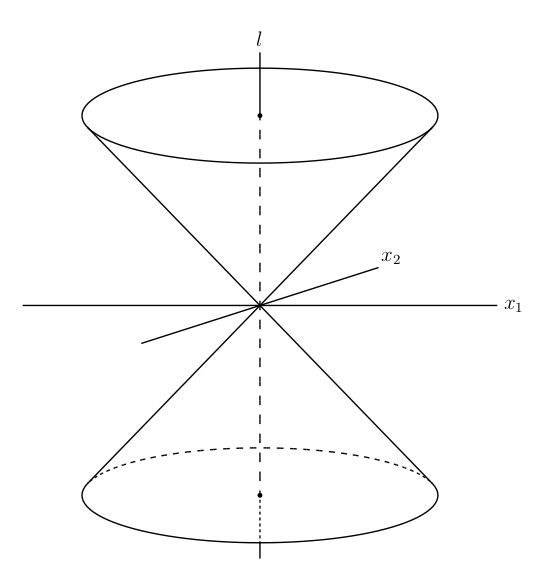
FIG. 1.
[9]That material velocities exceeding that of light are not possible, follows from the appearance of the radical in the special Lorentz
transformation (29).
By the introduction of the imaginary time variable, ,
Minkowski has made the theory of invariants for the four-dimensional
continuum of physical phenomena fully analogous
to the theory of invariants for the three-dimensional continuum
of Euclidean space. The theory of four-dimensional tensors of
special relativity differs from the theory of tensors in three-dimensional
space, therefore, only in the number of dimensions
and the relations of reality.
A physical entity which is specified by four quantities, ,
in an arbitrary inertial system of the
,
,
,
, is called
a 4-vector, with the components
, if the
correspond in
their relations of reality and the properties of transformation to
the
; it may be of the nature of a space or of a time. The
sixteen quantities
, then form the components of a tensor of
the second rank, if they transform according to the scheme
It follows from this that the
behave, with respect to
their properties of transformation and their properties of reality,
as the products of components,
of two 4-vectors,
(
) and (
). All the components are real except those which
contain the index 4 once, those being purely imaginary. Tensors
[Pg 41]
of the third and higher ranks may be defined in an analogous
way. The operations of addition, subtraction, multiplication,
contraction and differentiation for these tensors are wholly
analogous to the corresponding operations for tensors in three-dimensional space.
Before we apply the tensor theory to the four-dimensional space-time continuum, we shall examine more particularly the skew-symmetrical tensors. The tensor of the second rank has, in general, 16 = 4·4 components. In the case of skew-symmetry the components with two equal indices vanish, and the components with unequal indices are equal and opposite in pairs. There exist, therefore, only six independent components, as is the case in the electromagnetic field. In fact, it will be shown when we consider Maxwell's equations that these may be looked upon as tensor equations, provided we regard the electromagnetic field as a skew-symmetrical tensor. Further, it is clear that the skew-symmetrical tensor of the third rank (skew-symmetrical in all pairs of indices) has only four independent components, since there are only four combinations of three different indices.
We now turn to Maxwell's equations (19a), (19b), (20a),
(20b), and introduce the notation:[10]
with the convention that
shall be equal to
. Then
[Pg 42]
Maxwell's equations may be combined into the forms
as one can easily verify by substituting from (30a) and (31).
Equations (32) and (33) have a tensor character, and are
therefore co-variant with respect to Lorentz transformations,
if the
and the
have a tensor character, which we assume.
Consequently, the laws for transforming these quantities from
one to another allowable (inertial) system of co-ordinates are
uniquely determined. The progress in method which electrodynamics
owes to the theory of special relativity lies principally
in this, that the number of independent hypotheses is diminished.
If we consider, for example, equations (19a) only from the
standpoint of relativity of direction, as we have done above, we
see that they have three logically independent terms. The way
in which the electric intensity enters these equations appears to
be wholly independent of the way in which the magnetic intensity
enters them; it would not be surprising if instead of
,
we had, say,
or if this term were absent. On the other
hand, only two independent terms appear in equation (32). The
electromagnetic field appears as a formal unit; the way in which
the electric field enters this equation is determined by the way in
which the magnetic field enters it. Besides the electromagnetic
field, only the electric current density appears as an independent
entity. This advance in method arises from the fact that the
[Pg 43]
electric and magnetic fields draw their separate existences from
the relativity of motion. A field which appears to be purely an
electric field, judged from one system, has also magnetic field
components when judged from another inertial system. When
applied to an electromagnetic field, the general law of transformation
furnishes, for the special case of the special Lorentz
transformation, the equations
[10]In
order to avoid confusion from now on we shall use the three-dimensional
space indices, ,
,
instead of 1, 2, 3, and we shall reserve the
numeral indices 1, 2, 3, 4 for the four-dimensional space-time continuum.
If there exists with respect to only a magnetic field,
, but
no electric field,
, then with respect to
' there exists an electric
field
as well, which would act upon an electric particle at rest
relatively to
'. An observer at rest relatively to
would
designate this force as the Biot-Savart force, or the Lorentz electromotive
force. It therefore appears as if this electromotive force
had become fused with the electric field intensity into a single
entity.
In order to view this relation formally, let us consider the
expression for the force acting upon unit volume of electricity,
in which
is the vector velocity of electricity, with the velocity
of light as the unit. If we introduce
and
according to
(30a) and (31), we obtain for the first component the expression
[Pg 44]
Observing that
vanishes on account of the skew-symmetry of
the tensor (
), the components of
are given by the first three
components of the four-dimensional vector
and the fourth component is given by
There is, therefore, a four-dimensional vector of force per unit
volume, whose first three components,
,
,
, are
the ponderomotive force components per unit volume, and whose fourth
component is the rate of working of the field per unit volume,
multiplied by
.
A comparison of (36) and (35) shows that the theory of relativity
formally unites the ponderomotive force of the electric
field, , and the Biot-Savart or Lorentz force [
,
].
Mass and Energy. An important conclusion can be drawn
from the existence and significance of the 4-vector . Let us
imagine a body upon which the electromagnetic field acts for
a time. In the symbolic figure (Fig. 2)
designates the
-axis, and is at the same time a substitute for the three space axes
,
,
;
designates the real time axis. In this diagram
a body of finite extent is represented, at a definite time
, by
the interval
the whole space-time existence of the body is
represented by a strip whose boundary is everywhere inclined
less than 45° to the
-axis. Between the time sections,
=
and
=
, but not extending to them,
a portion of the strip is shaded. This represents the portion
of the space-time manifold
[Pg 45]
in which the electromagnetic field acts upon the body, or upon
the electric charges contained in it, the action upon them being
transmitted to the body. We shall now consider the changes
which take place in the momentum and energy of the body as a
result of this action.
FIG. 2.
We shall assume that the principles of momentum and
energy are valid for the body. The change in momentum,
,
,
, and the change
in energy,
are then given
[Pg 46]
by the expressions
Since the four-dimensional element of volume is an invariant,
and (
,
,
,
) forms a 4-vector, the four-dimensional
integral extended over the shaded portion transforms as a 4-vector,
as does also the integral between the limits
and
, because
the portion of the region which is not shaded contributes nothing
to the integral. It follows, therefore, that
,
,
,
form a 4-vector. Since the quantities themselves transform in
the same way as their increments, it follows that the aggregate
of the four quantities
has itself the properties of a vector; these quantities are referred
to an instantaneous condition of the body (e.g. at the time
=
).
This 4-vector may also be expressed in terms of the mass ,
and the velocity of the body, considered as a material particle.
To form this expression, we note first, that
[Pg 47]
is an invariant which refers to an infinitely short portion of the
four-dimensional line which represents the motion of the material
particle. The physical significance of the invariant
may
easily be given. If the time axis is chosen in such a way that it
has the direction of the line differential which we are considering,
or, in other words, if we reduce the material particle to rest,
we shall then have
; this will therefore be measured by
the light-seconds clock which is at the same place, and at rest
relatively to the material particle. We therefore call
the proper
time of the material particle. As opposed to
,
is therefore an
invariant, and is practically equivalent to
for motions whose
velocity is small compared to that of light. Hence we see that
has, just as the
, the character of a vector; we shall designate
(
) as the four-dimensional vector (in brief, 4-vector) of
velocity. Its components satisfy, by (38), the condition
We see that this 4-vector, whose components in the ordinary
notation are
is the only 4-vector which can be formed from the velocity components
of the material particle which are defined in three dimensions by
[Pg 48]
We therefore see that
must be that 4-vector which is to be equated to the 4-vector of
momentum and energy whose existence we have proved above.
By equating the components, we obtain, in three-dimensional
notation,
We recognize, in fact, that these components of momentum agree with those of classical mechanics for velocities which are small compared to that of light. For large velocities the momentum increases more rapidly than linearly with the velocity, so as to become infinite on approaching the velocity of light.
If we apply the last of equations (43) to a material particle
at rest ( = 0), we see that the energy,
of a, body at rest is
equal to its mass. Had we chosen the second as our unit of time,
we would have obtained
Mass and energy are therefore essentially alike; they are only
different expressions for the same thing. The mass of a body
[Pg 49]
is not a constant; it varies with changes in its energy.[11]
We see from the last of equations (43) that
becomes infinite when
approaches 1, the velocity of light. If we develop
in powers
of
, we obtain,
The second term of this expansion corresponds to the kinetic
energy of the material particle in classical mechanics.
[11]The emission of energy in radioactive processes is evidently connected with the fact that the atomic weights are not integers. Attempts have been made to draw conclusions from this concerning the structure and stability of the atomic nuclei.
Equations of Motion of Material Particles. From (43) we
obtain, by differentiating by the time , and using the principle
of momentum, in the notation of three-dimensional vectors,
This equation, which was previously employed by H. A.
Lorentz for the motion of electrons, has been proved to be true,
with great accuracy, by experiments with -rays.
Energy Tensor of the Electromagnetic Field. Before the development of the theory of relativity it was known that the principles of energy and momentum could be expressed in a differential form for the electromagnetic field. The four-dimensional formulation of these principles leads to an important conception, [Pg 50] that of the energy tensor, which is important for the further development of the theory of relativity.
If in the expression for the 4-vector of force per unit volume,
using the field equations (32), we express
in terms of the
field intensities,
, we obtain, after some transformations and
repeated application of the field equations (32) and (33), the
expression
where we have written[12]
[12]To be summed for the indices and
.
The physical meaning of equation (47) becomes evident if in
place of this equation we write, using a new notation,
[Pg 51]
or, on eliminating the imaginary,
When expressed in the latter form, we see that the first three
equations state the principle of momentum; ,...,
are the
Maxwell stresses in the electromagnetic field, and (
,
,
) is
the vector momentum per unit volume of the field. The last of
equations (47b) expresses the energy principle;
is the vector
flow of energy, and
the energy per unit volume of the field. In
fact, we get from (48) by introducing the well-known expressions
for the components of the field intensity from electrodynamics,
[Pg 52]
We conclude from (48) that the energy tensor of the electromagnetic
field is symmetrical; with this is connected the fact
that the momentum per unit volume and the how of energy are
equal to each other (relation between energy and inertia).
We therefore conclude from these considerations that the
energy per unit volume has the character of a tensor. This has
been proved directly only for an electromagnetic field, although
we may claim universal validity for it. Maxwell's equations determine
the electromagnetic field when the distribution of electric
charges and currents is known. But we do not know the
laws which govern the currents and charges. We do know, indeed,
that electricity consists of elementary particles (electrons,
positive nuclei), but from a theoretical point of view we cannot
comprehend this. We do not know the energy factors which
determine the distribution of electricity in particles of definite
size and charge, and all attempts to complete the theory in this
direction have failed. If then we can build upon Maxwell's equations
in general, the energy tensor of the electromagnetic field
is known only outside the charged particles.[13] In these regions,
outside of charged particles, the only regions in which we can believe
that we have the complete expression for the energy tensor,
we have, by (47),
[13]It has been attempted to remedy this lack of knowledge by considering the charged particles as proper singularities. But in my opinion this means giving up a real understanding of the structure of matter. It seems to me much better to give in to our present inability rather than to be satisfied by a solution that is only apparent.
[Pg 53]
General Expressions for the Conservation Principles. We
can hardly avoid making the assumption that in all other cases,
also, the space distribution of energy is given by a symmetrical
tensor, , and that this complete energy tensor everywhere
satisfies the relation (47c). At any rate we shall see that by
means of this assumption we obtain the correct expression for
the integral energy principle.
Let us consider a spatially bounded, closed system, which,
four-dimensionally, we may represent as a strip, outside of which
the vanish. Integrate equation (47c) over a space section.
Since the integrals of
,
and
vanish because
the
vanish at the limits of integration, we obtain
Inside the parentheses are the expressions for the momentum of
the whole system, multiplied by
, together with the negative
energy of the system, so that (49) expresses the conservation
principles in their integral form. That this gives the right conception
of energy and the conservation principles will be seen
from the following considerations.
PHENOMENOLOGICAL REPRESENTATION OF THE ENERGY TENSOR OF MATTER.
Hydrodynamical Equations. We know that matter is built
up of electrically charged particles, but we do not know the laws
which govern the constitution of these particles. In treating mechanical
problems, we are therefore obliged to make use of an
[Pg 54]
inexact description of matter, which corresponds to that of classical
mechanics. The density , of a material substance and the
hydrodynamical pressures are the fundamental concepts upon
which such a description is based.
FIG. 3.
Let be the density of matter at a place, estimated with
reference to a system of co-ordinates moving with the matter.
Then
, the density at rest, is an invariant. If we think of the
matter in arbitrary motion and neglect the pressures (particles
of dust in vacuo, neglecting the size of the particles and the
temperature), then the energy tensor will depend only upon the
[Pg 55]
velocity components,
and
. We secure the tensor character
of
by putting
in which the
, in the three-dimensional representation, are
given by (41). In fact, it follows from (50) that for
,
(equal to the negative energy per unit volume), as it should,
according to the theorem of the equivalence of mass and energy,
and according to the physical interpretation of the energy tensor
given above. If an external force (four-dimensional vector,
)
acts upon the matter, by the principles of momentum and energy
the equation
must hold. We shall now show that this equation leads to the
same law of motion of a material particle as that already obtained.
Let us imagine the matter to be of infinitely small extent
in space, that is, a four-dimensional thread; then by integration
over the whole thread with respect to the space co-ordinates
,
,
, we obtain
Now is an invariant, as is, therefore, also
.
We shall calculate this integral, first with
respect to the inertial system which we have chosen, and second,
with respect to a system relatively to which the matter has the
velocity zero. The integration is to be extended over a filament
[Pg 56]
of the thread for which
may be regarded as constant over the
whole section. If the space volumes of the filament referred to
the two systems are
and
respectively, then we have
and therefore also
If we substitute the right-hand side for the left-hand side in
the former integral, and put outside the sign of integration,
we obtain,
We see, therefore, that the generalized conception of the energy
tensor is in agreement with our former result.
The Eulerian Equations for Perfect Fluids. In order to get
nearer to the behaviour of real matter we must add to the energy
tensor a term which corresponds to the pressures. The simplest
case is that of a perfect fluid in which the pressure is determined
by a scalar . Since the tangential stresses
, etc., vanish in
this case, the contribution to the energy tensor must be of the
form
. We must therefore put
[Pg 57]
At rest, the density of the matter, or the energy per unit volume,
is in this case, not
but
. For
In the absence of any force, we have
If we multiply this equation by
and sum for the
's we obtain, using (40),
where we have put
.
This is the equation of continuity, which differs from that of
classical mechanics by the term
, which, practically,
is vanishingly small. Observing (52), the conservation principles take the form
The equations for the first three indices evidently correspond to
the Eulerian equations. That the equations (52) and (53) correspond,
to a first approximation, to the hydrodynamical equations
of classical mechanics, is a further confirmation of the generalized
energy principle. The density of matter and of energy
has the character of a symmetrical tensor.
[Pg 58]
ALL of the previous considerations have been based upon the assumption that all inertial systems are equivalent for the description of physical phenomena, but that they are preferred, for the formulation of the laws of nature, to spaces of reference in a different state of motion. We can think of no cause for this preference for definite states of motion to all others, according to our previous considerations, either in the perceptible bodies or in the concept of motion; on the contrary, it must be regarded as an independent property of the space-time continuum. The principle of inertia, in particular, seems to compel us to ascribe physically objective properties to the space-time continuum. Just as it was necessary from the Newtonian standpoint to make both the statements, tempus est absolutum, spatium est absolutum, so from the standpoint of the special theory of relativity we must say, continuum spatii et temporis est absolutum. In this latter statement absolutum means not only "physically real," but also "independent in its physical properties, having a physical effect, but not itself influenced by physical conditions."
As long as the principle of inertia is regarded as the keystone of physics, this standpoint is certainly the only one which is justified. But there are two serious criticisms of the ordinary conception. In the first place, it is contrary to the mode of thinking in science to conceive of a thing (the space-time continuum) which acts itself, but which cannot be acted upon. This is the reason why E. Mach was led to make the attempt to eliminate space as an active cause in the system of mechanics. According [Pg 59] to him, a material particle does not move in unaccelerated motion relatively to space, but relatively to the centre of all the other masses in the universe; in this way the series of causes of mechanical phenomena was closed, in contrast to the mechanics of Newton and Galileo. In order to develop this idea within the limits of the modern theory of action through a medium, the properties of the space-time continuum which determine inertia must be regarded as field properties of space, analogous to the electromagnetic field. The concepts of classical mechanics afford no way of expressing this. For this reason Mach's attempt at a solution failed for the time being. We shall come back to this point of view later. In the second place, classical mechanics indicates a limitation which directly demands an extension of the principle of relativity to spaces of reference which are not in uniform motion relatively to each other. The ratio of the masses of two bodies is defined in mechanics in two ways which differ from each other fundamentally; in the first place, as the reciprocal ratio of the accelerations which the same motional force imparts to them (inert mass), and in the second place, as the ratio of the forces which act upon them in the same gravitational field (gravitational mass). The equality of these two masses, so differently defined, is a fact which is confirmed by experiments of very high accuracy (experiments of Eötvös), and classical mechanics offers no explanation for this equality. It is, however, clear that science is fully justified in assigning such a numerical equality only after this numerical equality is reduced to an equality of the real nature of the two concepts.
That this object may actually be attained by an extension
of the principle of relativity, follows from the following consideration.
A little reflection will show that the theorem of the
[Pg 60]
equality of the inert and the gravitational mass is equivalent
to the theorem that the acceleration imparted to a body by a
gravitational field is independent of the nature of the body. For
Newton's equation of motion in a gravitational field, written out
in full, is
It is only when there is numerical equality between the inert
and gravitational mass that the acceleration is independent of
the nature of the body. Let now
be an inertial system. Masses
which are sufficiently far from each other and from other bodies
are then, with respect to
, free from acceleration. We shall
also refer these masses to a system of co-ordinates
' uniformly
accelerated with respect to
. Relatively to
' all the masses
have equal and parallel accelerations; with respect to
' they
behave just as if a gravitational field were present and
' were
unaccelerated. Overlooking for the present the question as to the
"cause" of such a gravitational field, which will occupy us later,
there is nothing to prevent our conceiving this gravitational field
as real, that is, the conception that
' is "at rest" and a gravitational
field is present we may consider as equivalent to the conception
that only
is an "allowable" system of co-ordinates and
no gravitational field is present. The assumption of the complete
physical equivalence of the systems of co-ordinates,
and
',
we call the "principle of equivalence;" this principle is evidently
intimately connected with the theorem of the equality between
the inert and the gravitational mass, and signifies an extension
of the principle of relativity to co-ordinate systems which are in
[Pg 61]
non-uniform motion relatively to each other. In fact, through
this conception we arrive at the unity of the nature of inertia
and gravitation. For according to our way of looking at it, the
same masses may appear to be either under the action of inertia
alone (with respect to
) or under the combined action of
inertia and gravitation (with respect to
'). The possibility of
explaining the numerical equality of inertia and gravitation by
the unity of their nature gives to the general theory of relativity,
according to my conviction, such a superiority over the conceptions
of classical mechanics, that all the difficulties encountered
in development must be considered as small in comparison.
What justifies us in dispensing with the preference for inertial systems over all other co-ordinate systems, a preference that seems so securely established by experiment based upon the principle of inertia? The weakness of the principle of inertia lies in this, that it involves an argument in a circle: a mass moves without acceleration if it is sufficiently far from other bodies; we know that it is sufficiently far from other bodies only by the fact that it moves without acceleration. Are there, in general, any inertial systems for very extended portions of the space-time continuum, or, indeed, for the whole universe? We may look upon the principle of inertia as established, to a high degree of approximation, for the space of our planetary system, provided that we neglect the perturbations due to the sun and planets. Stated more exactly, there are finite regions, where, with respect to a suitably chosen space of reference, material particles move freely without acceleration, and in which the laws of the special theory of relativity, which have been developed above, hold with remarkable accuracy. Such regions we shall call "Galilean regions." We shall proceed from the consideration of such regions [Pg 62] as a special case of known properties.
The principle of equivalence demands that in dealing with
Galilean regions we may equally well make use of non-inertial
systems, that is, such co-ordinate systems as, relatively to inertial
systems, are not free from acceleration and rotation. If,
further, we are going to do away completely with the difficult
question as to the objective reason for the preference of certain
systems of co-ordinates, then we must allow the use of arbitrarily
moving systems of co-ordinates. As soon as we make this
attempt seriously we come into conflict with that physical interpretation
of space and time to which we were led by the special
theory of relativity. For let ' be a system of co-ordinates whose
'-axis coincides with the
-axis of
, and which rotates about
the latter axis with constant angular velocity. Are the configurations
of rigid bodies, at rest relatively to
', in accordance with
the laws of Euclidean geometry? Since
' is not an inertial system,
we do not know directly the laws of configuration of rigid
bodies with respect to
', nor the laws of nature, in general. But
we do know these laws with respect to the inertial system
,
and we can therefore estimate them with respect to
'. Imagine
a circle drawn about the origin in the
plane of
' and a
diameter of this circle. Imagine, further, that we have given a
large number of rigid rods, all equal to each other. We suppose
these laid in series along the periphery and the diameter of the
circle, at rest relatively to
'. If
is the number of these rods
along the periphery,
the number along the diameter, then, if
' does not rotate relatively to
, we shall have
[Pg 63]
But if
' rotates we get a different result. Suppose that at
a definite time
of
we determine the ends of all the rods.
With respect to
all the rods upon the periphery experience
the Lorentz contraction, but the rods upon the diameter do not
experience this contraction (along their lengths!).[14]
It therefore follows that
It therefore follows that the laws of configuration of rigid
bodies with respect to ' do not agree with the laws of configuration
of rigid bodies that are in accordance with Euclidean geometry.
If, further, we place two similar clocks (rotating with
'),
one upon the periphery, and the other at the centre of the circle,
then, judged from
, the clock on the periphery will go
slower than the clock at the centre. The same thing must take
place, judged from
', if we define time with respect to
' in a
not wholly unnatural way, that is, in such a way that the laws
with respect to
' depend explicitly upon the time. Space and
time, therefore, cannot be defined with respect to
' as they
were in the special theory of relativity with respect to inertial
systems. But, according to the principle of equivalence,
' is
also to be considered as a system at rest, with respect to which
there is a gravitational field (field of centrifugal force, and force
of Coriolis). We therefore arrive at the result: the gravitational
field influences and even determines the metrical laws of the
space-time continuum. If the laws of configuration of ideal rigid
bodies are to be expressed geometrically, then in the presence
of a gravitational field the geometry is not Euclidean.
[14]These considerations assume that the behaviour of rods and clocks depends only upon velocities, and not upon accelerations, or, at least, that the influence of acceleration does not counteract that of velocity.
[Pg 64]
The case that we have been considering is analogous to that
which is presented in the two-dimensional treatment of surfaces.
It is impossible in the latter case also, to introduce co-ordinates
on a surface (e.g. the surface of an ellipsoid) which
have a simple metrical significance, while on a plane the Cartesian
co-ordinates, ,
, signify directly lengths measured by a
unit measuring rod. Gauss overcame this difficulty, in his theory
of surfaces, by introducing curvilinear co-ordinates which,
apart from satisfying conditions of continuity, were wholly arbitrary,
and afterwards these co-ordinates were related to the
metrical properties of the surface. In an analogous way we
shall introduce in the general theory of relativity arbitrary co-ordinates,
,
,
,
, which shall number uniquely the space-time
points, so that neighbouring events are associated with
neighbouring values of the co-ordinates; otherwise, the choice
of co-ordinates is arbitrary. We shall be true to the principle
of relativity in its broadest sense if we give such a form to the
laws that they are valid in every such four-dimensional system
of co-ordinates, that is, if the equations expressing the laws are
co-variant with respect to arbitrary transformations.
The most important point of contact between Gauss's theory
of surfaces and the general theory of relativity lies in the metrical
properties upon which the concepts of both theories, in the
main, are based. In the case of the theory of surfaces, Gauss's
argument is as follows. Plane geometry may be based upon the
concept of the distance , between two indefinitely near points.
The concept of this distance is physically significant because
the distance can be measured directly by means of a rigid measuring
rod. By a suitable choice of Cartesian co-ordinates this
[Pg 65]
distance may be expressed by the formula
.
We may base upon this quantity the concepts of the straight
line as the geodesic (
), the interval, the circle, and the
angle, upon which the Euclidean plane geometry is built. A
geometry may be developed upon another continuously curved
surface, if we observe that an infinitesimally small portion of the
surface may be regarded as plane, to within relatively infinitesimal
quantities. There are Cartesian co-ordinates,
,
, upon
such a small portion of the surface, and the distance between
two points, measured by a measuring rod, is given by
If we introduce arbitrary curvilinear co-ordinates,
,
, on the
surface, then
,
, may be expressed linearly in terms of
,
. Then everywhere upon the surface we have
where
,
,
are determined by the nature of the surface
and the choice of co-ordinates; if these quantities are known,
then it is also known how networks of rigid rods may be laid
upon the surface. In other words, the geometry of surfaces may
be based upon this expression for
exactly as plane geometry
is based upon the corresponding expression.
There are analogous relations in the four-dimensional space-time
continuum of physics. In the immediate neighbourhood of
an observer, falling freely in a gravitational field, there exists no
gravitational field. We can therefore always regard an infinitesimally
small region of the space-time continuum as Galilean.
For such an infinitely small region there will be an inertial system
(with the space co-ordinates, ,
,
, and the time
[Pg 66]
co-ordinate
) relatively to which we are to regard the laws of
the special theory of relativity as valid. The quantity which is
directly measurable by our unit measuring rods and clocks,
or its negative,
is therefore a uniquely determinate invariant for two neighbouring
events (points in the four-dimensional continuum), provided
that we use measuring rods that are equal to each other when
brought together and superimposed, and clocks whose rates are
the same when they are brought together. In this the physical
assumption is essential that the relative lengths of two measuring
rods and the relative rates of two clocks are independent, in
principle, of their previous history. But this assumption is certainly
warranted by experience; if it did not hold there could be
no sharp spectral lines; for the single atoms of the same element
certainly do not have the same history, and it would be absurd
to suppose any relative difference in the structure of the single
atoms due to their previous history if the mass and frequencies
of the single atoms of the same element were always the same.
Space-time regions of finite extent are, in general, not
Galilean, so that a gravitational field cannot be done away
with by any choice of co-ordinates in a finite region. There
is, therefore, no choice of co-ordinates for which the metrical
relations of the special theory of relativity hold in a finite region.
But the invariant always exists for two neighbouring
points (events) of the continuum. This invariant
may be
[Pg 67]
expressed in arbitrary co-ordinates. If one observes that the
local
may be expressed linearly in terms of the co-ordinate
differentials
,
may be expressed in the form
The functions describe, with respect to the arbitrarily
chosen system of co-ordinates, the metrical relations of the
space-time continuum and also the gravitational field. As in
the special theory of relativity, we have to discriminate between
time-like and space-like line elements in the four-dimensional
continuum; owing to the change of sign introduced, time-like line
elements have a real, space-like line elements an imaginary
.
The time-like
can be measured directly by a suitably chosen
clock.
According to what has been said, it is evident that the formulation of the general theory of relativity assumes a generalization of the theory of invariants and the theory of tensors; the question is raised as to the form of the equations which are co-variant with respect to arbitrary point transformations. The generalized calculus of tensors was developed by mathematicians long before the theory of relativity. Riemann first extended Gauss's train of thought to continua of any number of dimensions; with prophetic vision he saw the physical meaning of this generalization of Euclid's geometry. Then followed the development of the theory in the form of the calculus of tensors, particularly by Ricci and Levi-Civita. This is the place for a brief presentation of the most important mathematical concepts and operations of this calculus of tensors.
We designate four quantities, which are defined as functions
of the with respect to every system of co-ordinates, as components,
[Pg 68]
, of a contra-variant vector, if they transform in a
change of co-ordinates as the co-ordinate differentials
. We
therefore have
Besides these contra-variant vectors, there are also co-variant
vectors. If
are the components of a co-variant vector, these
vectors are transformed according to the rule
The definition of a co-variant vector is chosen in such a way that
a co-variant vector and a contra-variant vector together form a
scalar according to the scheme,
Accordingly,
In particular, the derivatives
of a scalar
, are components
of a co-variant vector, which, with the co-ordinate differentials,
form the scalar
;
we see from this example how natural
is the definition of the co-variant vectors.
There are here, also, tensors of any rank, which may have
co-variant or contra-variant character with respect to each index;
as with vectors, the character is designated by the position
[Pg 69]
of the index. For example, denotes a tensor of the second
rank, which is co-variant with respect to the index
, and contra-variant
with respect to the index
. The tensor character indicates
that the equation of transformation is
Tensors may be formed by the addition and subtraction of
tensors of equal rank and like character, as in the theory of
invariants of orthogonal linear substitutions, for example,
The proof of the tensor character of
depends upon (58).
Tensors may be formed by multiplication, keeping the character
of the indices, just as in the theory of invariants of linear
orthogonal transformations, for example,
The proof follows directly from the rule of transformation.
Tensors may be formed by contraction with respect to two
indices of different character, for example,
The tensor character of
determines the tensor character
of
. Proof—
[Pg 70]
The properties of symmetry and skew-symmetry of a tensor with respect to two indices of like character have the same significance as in the theory of invariants.
With this, everything essential has been said with regard to the algebraic properties of tensors.
The Fundamental Tensor. It follows from the invariance
of for an arbitrary choice of the
, in connexion with
the condition of symmetry consistent with (55), that the
are components of a symmetrical co-variant tensor (Fundamental
Tensor). Let us form the determinant,
, of the
, and
also the minors, divided by
, corresponding to the single
.
These minors, divided by
, will be denoted by
, and their
co-variant character is not yet known. Then we have
If we form the infinitely small quantities (co-variant vectors)
multiply by
and sum over the
, we obtain, by the use
of (62),
Since the ratios of the
, are arbitrary, and the
as well as
the
are components of vectors, it follows that the
are the
components of a contra-variant tensor[15]
(contra-variant fundamental tensor).
The tensor character of
(mixed fundamental
[Pg 71]
tensor) accordingly follows, by (62). By means of the fundamental
tensor, instead of tensors with co-variant index character, we
can introduce tensors with contra-variant index character, and
conversely. For example,
[15]If we multiply (64)
by ,
sum over the
, and replace the
by
a transformation to the accented system, we obtain
The statement made above follows from this, since, by (64), we must also
have
and both equations
must hold for every choice of
.
Volume Invariants. The volume element
is not an invariant. For by Jacobi's theorem,
But we can complement
so that it becomes an invariant. If
we form the determinant of the quantities
[Pg 72]
we obtain, by a double application of the theorem of multiplication
of determinants,
We therefore get the invariant,
Formation of Tensors by Differentiation. Although the algebraic
operations of tensor formation have proved to be as
simple as in the special case of invariance with respect to linear
orthogonal transformations, nevertheless in the general case,
the invariant differential operations are, unfortunately, considerably
more complicated. The reason for this is as follows. If
is a contra-variant vector, the coefficients of its
transformation,
, are
independent of position only if the transformation
is a linear one. For then the vector components,
,
at a neighbouring point transform in the same way as the
,
from which follows the vector character of the vector differentials,
and the tensor character of
.
But if the
are variable this is no longer true.
That there are, nevertheless, in the general case, invariant
differential operations for tensors, is recognized most satisfactorily
in the following way, introduced by Levi-Civita and Weyl.
Let () be a contra-variant vector whose components are given
with respect to the co-ordinate system of the
.
Let
and
[Pg 73]
be two infinitesimally near points of the continuum. For the infinitesimal
region surrounding the point
, there is, according
to our way of considering the matter, a co-ordinate system of
the
(with imaginary
-co-ordinate) for which the
continuum is Euclidean. Let
be the co-ordinates of the vector at
the point
. Imagine a vector drawn at the point
, using the
local system of the
, with the same co-ordinates (parallel vector
through
), then this parallel vector is uniquely determined
by the vector at
and the displacement. We designate this operation,
whose uniqueness will appear in the sequel, the parallel
displacement of the vector
from
to the infinitesimally near
point
. If we form the vector difference of the vector (
) at
the point
and the vector obtained by parallel displacement
from
to
, we get a vector which may be regarded as the
differential of the vector (
) for the given displacement
.
This vector displacement can naturally also be considered
with respect to the co-ordinate system of the . If
are the
co-ordinates of the vector at
,
the co-ordinates of
the vector displaced to
along the interval (
), then
the
do not vanish in this case. We know of these quantities, which
do not have a vector character, that they must depend linearly
and homogeneously upon the
and the
. We therefore put
In addition, we can state that the must be symmetrical
with respect to the indices
and
.
For we can assume from
a representation by the aid of a Euclidean system of local co-ordinates
that the same parallelogram will be described by the
displacement of an element
along a second element
[Pg 74]
as by a displacement of
along
.
We must therefore have
The statement made above follows from this, after interchanging
the indices of summation,
and
, on the right-hand side.
Since the quantities determine all the metrical properties
of the continuum, they must also determine the
. If we
consider the invariant of the vector
that is, the square of its
magnitude,
which is an invariant, this cannot change in a parallel displacement.
We therefore have
or, by (67),
Owing to the symmetry of the expression in the brackets
with respect to the indices and
, this equation can be valid
for an arbitrary choice of the vectors (
) and
only when
the expression in the brackets vanishes for all combinations of
the indices. By a cyclic interchange of the indices
,
,
, we
obtain thus altogether three equations, from which we obtain,
on taking into account the symmetrical property of the
,
[Pg 75]
in which, following Christoffel, the abbreviation has been used,
If we multiply (68) by and sum over the
, we obtain
in which
is
the Christoffel symbol of the second kind.
Thus the quantities
are deduced from the
. Equations
(67) and (70) are the foundation for the following discussion.
Co-variant Differentiation of Tensors. If () is
the vector resulting from an infinitesimal parallel displacement
from
to
, and (
) the vector
at
the point
,
then the difference of these two,
is also a vector. Since this is the case for an arbitrary choice of
the
, it follows that
is a tensor, which we designate as the co-variant derivative of
the tensor of the first rank (vector). Contracting this tensor, we
obtain the divergence of the contra-variant tensor
. In this
we must observe that according to (70),
[Pg 76]
If we put, further,
a quantity designated by Weyl as the contra-variant tensor density[16]
of the first rank, it follows that,
is a scalar density.
[16]This expression is justified, in that
has a tensor
character. Every tensor, when multiplied by
, changes into a tensor
density. We employ capital Gothic letters for tensor densities.
We get the law of parallel displacement for the co-variant
vector by stipulating that the parallel displacement shall be
effected in such a way that the scalar
remains unchanged, and that therefore
vanishes for every value assigned to (
). We therefore get
From this we arrive at the co-variant derivative of the co-variant
vector by the same process as that which led to (71),
[Pg 77]
By interchanging the indices
and
, and subtracting, we get
the skew-symmetrical tensor,
For the co-variant differentiation of tensors of the second
and higher ranks we may use the process by which (75) was
deduced. Let, for example, () be a co-variant tensor of the
second rank. Then
is a scalar,
if
and
are vectors.
This expression must not be changed by the
-displacement;
expressing this by a formula, we get, using (67),
, whence
we get the desired co-variant derivative,
In order that the general law of co-variant differentiation of
tensors may be clearly seen, we shall write down two co-variant
derivatives deduced in an analogous way:
The general law of formation now becomes evident. From these
formulae we shall deduce some others which are of interest for
the physical applications of the theory.
In case is skew-symmetrical, we obtain the tensor
[Pg 78]
which is skew-symmetrical in all pairs of indices, by cyclic
interchange and addition.
If, in (78), we replace by the fundamental tensor,
,
then the right-hand side vanishes identically; an analogous statement
holds for (80) with respect to
; that is, the co-variant
derivatives of the fundamental tensor vanish. That this must be
so we see directly in the local system of co-ordinates.
In case is skew-symmetrical, we obtain from (80), by
contraction with respect to
and
,
In the general case, from (79) and (80), by contraction with
respect to and
, we obtain the equations,
The Riemann Tensor. If we have given a curve extending
from the point to the point
of the continuum, then a
vector
, given at
, may, by a parallel displacement, be moved
along the curve to
. If the continuum is Euclidean (more generally,
if by a suitable choice of co-ordinates the
, are constants)
then the vector obtained at
as a result of this displacement
does not depend upon the choice of the curve joining
and
.
But otherwise, the result depends upon the path of the displacement.
FIG.4.
In this case, therefore, a vector suffers a change,
(in its direction, not its magnitude), when it is carried from a
[Pg 79]
point
of a closed curve, along the curve, and back to P. We
shall now calculate this vector change:
As in Stokes' theorem for the line integral of a vector around
a closed curve, this problem may be reduced to the integration
around a closed curve with infinitely small linear dimensions; we
shall limit ourselves to this case.
We have, first, by (67),
In this, is the value of
this quantity at the variable
point
of the path of integration. If we put
[Pg 80]
and denote the value of
at
by
then we have, with
sufficient accuracy,
Let, further, be the value obtained from
by a parallel
displacement along the curve from
to
. It may now easily
be proved by means of (67) that
-
is infinitely small of
the first order, while, for a curve of infinitely small dimensions
of the first order,
is infinitely small of the second order.
Therefore there is an error of only the second order if we put
If we introduce these values of
and
into the integral,
we obtain, neglecting all quantities of a higher order of small
quantities than the second,
The quantity removed from under the sign of integration refers
to the point
. Subtracting
from the integrand, we
obtain
This skew-symmetrical tensor of the second rank,
, characterizes
the surface element bounded by the curve in magnitude
and position. If the expression in the brackets in (85) were
skew-symmetrical with respect to the indices
and
, we could
[Pg 81]
conclude its tensor character from (85). We can accomplish this
by interchanging the summation indices
and
in (85) and
adding the resulting equation to (85). We obtain
in which
The tensor character of follows from (86); this is the
Riemann curvature tensor of the fourth rank, whose properties of
symmetry we do not need to go into. Its vanishing is a sufficient
condition (disregarding the reality of the chosen co-ordinates)
that the continuum is Euclidean.
By contraction of the Riemann tensor with respect to the
indices ,
, we obtain the symmetrical tensor of the second
rank,
The last two terms vanish if the system of co-ordinates is so
chosen that
. From
, we can form the scalar,
Straightest Geodetic Lines. A line may be constructed in
such a way that its successive elements arise from each other by
parallel displacements. This is the natural generalization of the
straight line of the Euclidean geometry. For such a line, we have
[Pg 82]
The left-hand side is to be replaced by
,[17]
so that we have
We get the same line if we find the line which gives a stationary
value to the integral
between two points (geodetic line).
[17]The direction vector at a neighbouring point of the curve results, by
a parallel displacement along the line element (), from the direction
vector of each point considered.
[Pg 83]
WE are now in possession of the mathematical apparatus which is necessary to formulate the laws of the general theory of relativity. No attempt will be made in this presentation at systematic completeness, but single results and possibilities will be developed progressively from what is known and from the results obtained. Such a presentation is most suited to the present provisional state of our knowledge.
A material particle upon which no force acts moves, according
to the principle of inertia, uniformly in a straight line. In
the four-dimensional continuum of the special theory of relativity
(with real time co-ordinate) this is a real straight line. The
natural, that is, the simplest, generalization of the straight line
which is plausible in the system of concepts of Riemann's general
theory of invariants is that of the straightest, or geodetic,
line. We shall accordingly have to assume, in the sense of the
principle of equivalence, that the motion of a material particle,
under the action only of inertia and gravitation, is described by
the equation,
In fact, this equation reduces to that of a straight line if all the
components,
, of the gravitational field vanish.
How are these equations connected with Newton's equations
of motion? According to the special theory of relativity,
the as well as the
, have
the values, with respect to an inertial
[Pg 84]
system (with real time co-ordinate and suitable choice of the
sign of
),
The equations of motion then become
We shall call this the "first approximation" to the
-field. In
considering approximations it is often useful, as in the special
theory of relativity, to use an imaginary
-co-ordinate, as then
the
. to the first approximation, assume the values
These values may be collected in the relation
To the second approximation we must then put
where the
are to be regarded as small of the first order.
[Pg 85]
Both terms of our equation of motion are then small of the
first order. If we neglect terms which, relatively to these, are
small of the first order, we have to put
We shall now introduce an approximation of a second kind. Let
the velocity of the material particles be very small compared to
that of light. Then
will be the same as the time differential,
.
Further,
,
,
will vanish compared to
.
We shall assume, in addition, that the gravitational field varies
so little with the time that the derivatives of the
by
may
be neglected. Then the equation of motion (for
= 1,2,3)
reduces to
This equation is identical with Newton's equation of motion for
a material particle in a gravitational field, if we identify
with the potential of the gravitational field; whether or not this
is allowable, naturally depends upon the field equations of gravitation,
that is, it depends upon whether or not this quantity
satisfies, to a first approximation, the same laws of the field
as the gravitational potential in Newton's theory. A glance at
(90) and (90a) shows that the
actually do play the rôle of
the intensity of the gravitational field. These quantities do not
have a tensor character.
Equations (90) express the influence of inertia and gravitation upon the material particle. The unity of inertia and gravitation [Pg 86] is formally expressed by the fact that the whole left-hand side of (90) has the character of a tensor (with respect to any transformation of co-ordinates), but the two terms taken separately do not have tensor character, so that, in analogy with Newton's equations, the first term would be regarded as the expression for inertia, and the second as the expression for the gravitational force.
We must next attempt to find the laws of the gravitational
field. For this purpose, Poisson's equation,
of the Newtonian theory must serve as a model. This equation
has its foundation in the idea that the gravitational field
arises from the density
of ponderable matter. It must also
be so in the general theory of relativity. But our investigations
of the special theory of relativity have shown that in place of
the scalar density of matter we have the tensor of energy per
unit volume. In the latter is included not only the tensor of
the energy of ponderable matter, but also that of the electromagnetic
energy. We have seen, indeed, that in a more complete
analysis the energy tensor can be regarded only as a provisional
means of representing matter. In reality, matter consists of electrically
charged particles, and is to be regarded itself as a part,
in fact, the principal part, of the electromagnetic field. It is
only the circumstance that we have not sufficient knowledge of
the electromagnetic field of concentrated charges that compels
us, provisionally, to leave undetermined in presenting the theory,
the true form of this tensor. From this point of view our
problem now is to introduce a tensor,
. of the second rank,
[Pg 87]
whose structure we do not know provisionally, and which includes
in itself the energy density of the electromagnetic field
and of ponderable matter; we shall denote this in the following
as the "energy tensor of matter."
According to our previous results, the principles of momentum
and energy are expressed by the statement that the divergence
of this tensor vanishes (47c). In the general theory of relativity,
we shall have to assume as valid the corresponding general
co-variant equation. If () denotes the co-variant energy tensor
of matter,
the corresponding mixed tensor density, then,
in accordance with (83), we must require that
be satisfied. It must be remembered that besides the energy density
of the matter there must also be given an energy density of
the gravitational field, so that there can be no talk of principles
of conservation of energy and momentum for matter alone. This
is expressed mathematically by the presence of the second term
in (95), which makes it impossible to conclude the existence of
an integral equation of the form of (49). The gravitational field
transfers energy and momentum to the "matter," in that it exerts
forces upon it and gives it energy; this is expressed by the
second term in (95).
If there is an analogue of Poisson's equation in the general
theory of relativity, then this equation must be a tensor equation
for the tensor of the gravitational potential; the energy
tensor of matter must appear on the right-hand side of this
equation. On the left-hand side of the equation there must be
a differential tensor in the
. We have to find this differential
[Pg 88]
tensor. It is completely determined by the following three
conditions:—
1. It may contain no differential coefficients of the higher
than the second.
2. It must be linear and homogeneous in these second differential coefficients.
3. Its divergence must vanish identically.
The first two of these conditions are naturally taken from
Poisson's equation. Since it may be proved mathematically
that all such differential tensors can be formed algebraically
(i.e. without differentiation) from Riemann's tensor, our tensor
must be of the form
in which
and
are defined by (88) and (89) respectively.
Further, it may be proved that the third condition requires a
to have the value
. For the law of the gravitational field we
therefore get the equation
Equation (95) is a consequence of this equation.
denotes a
constant, which is connected with the Newtonian gravitation
constant.
In the following I shall indicate the features of the theory
which are interesting from the point of view of physics, using as
little as possible of the rather involved mathematical method.
It must first be shown that the divergence of the left-hand side
actually vanishes. The energy principle for matter may be expressed, by (83),
[Pg 89]
in which
The analogous operation, applied to the left-hand side of (96),
will lead to an identity.
In the region surrounding each world-point there are systems
of co-ordinates for which, choosing the -co-ordinate imaginary,
at the given point,
and for which the first derivatives of the
and the
vanish.
We shall verify the vanishing of the divergence of the left-hand
side at this point. At this point the components
vanish, so
that we have to prove the vanishing only of
Introducing (88) and (70) into this expression, we see that the
only terms that remain are those in which third derivatives of
the
enter. Since the
are to be replaced by
, we obtain,
finally, only a few terms which may easily be seen to cancel
each other. Since the quantity that we have formed has a tensor
character, its vanishing is proved for every other system of co-ordinates
also, and naturally for every other four-dimensional
point. The energy principle of matter (97) is thus a mathematical
consequence of the field equations (96).
In order to learn whether the equations (96) are consistent
with experience, we must, above all else, find out whether they
[Pg 90]
lead to the Newtonian theory as a first approximation. For this
purpose we must introduce various approximations into these
equations. We already know that Euclidean geometry and the
law of the constancy of the velocity of light are valid, to a certain
approximation, in regions of a great extent, as in the planetary
system. If, as in the special theory of relativity, we take the
fourth co-ordinate imaginary, this means that we must put
in which the
are so small compared to 1 that we can neglect
the higher powers of the
and their derivatives. If we do this,
we learn nothing about the structure of the gravitational held, or
of metrical space of cosmical dimensions, but we do learn about
the influence of neighbouring masses upon physical phenomena.
Before carrying through this approximation we shall transform
(96). We multiply (96) by , summed over the
and
observing the relation which follows from the definition of
the
,
we obtain the equation
If we put this value of
in (96) we obtain
When the approximation which has been mentioned is carried
out, we obtain for the left-hand side,
[Pg 91]
or
in which has been put
We must now note that equation (96) is valid for any system
of co-ordinates. We have already specialized the system of
co-ordinates in that we have chosen it so that within the region
considered the differ infinitely little from the constant values
. But this condition remains satisfied in any infinitesimal
change of co-ordinates, so that there are still four conditions
to which the
may be subjected, provided these conditions
do not conflict with the conditions for the order of magnitude of
the
. We shall now assume that the system of co-ordinates
is so chosen that the four relations—
are satisfied. Then (96a) takes the form
These equations may be solved by the method, familiar in
electrodynamics, of retarded potentials; we get, in an easily
understood notation,
[Pg 92]
In order to see in what sense this theory contains the Newtonian
theory, we must consider in greater detail the energy
tensor of matter. Considered phenomenologically, this energy
tensor is composed of that of the electromagnetic field and of
matter in the narrower sense. If we consider the different parts
of this energy tensor with respect to their order of magnitude,
it follows from the results of the special theory of relativity that
the contribution of the electromagnetic field practically vanishes
in comparison to that of ponderable matter. In our system of
units, the energy of one gram of matter is equal to 1, compared
to which the energy of the electric fields may be ignored, and
also the energy of deformation of matter, and even the chemical
energy. We get an approximation that is fully sufficient for our
purpose if we put
In this,
is the density at rest, that is, the density of the ponderable
matter, in the ordinary sense, measured with the aid
of a unit measuring rod, and referred to a Galilean system of
co-ordinates moving with the matter.
We observe, further, that in the co-ordinates we have chosen,
we shall make only a relatively small error if we replace the
by
, so that we put
The previous developments are valid however rapidly the
masses which generate the field may move relatively to our chosen
system of quasi-Galilean co-ordinates. But in astronomy
[Pg 93]
we have to do with masses whose velocities, relatively to the
co-ordinate system employed, are always small compared to the
velocity of light, that is, small compared to 1, with our choice
of the unit of time. We therefore get an approximation which is
sufficient for nearly all practical purposes if in (101) we replace
the retarded potential by the ordinary (non-retarded) potential,
and if, for the masses which generate the field, we put
Then we get for
and
the values
For
we get the value
, and, finally,
for
the values,
We thus get, from (101),
[Pg 94]
while all the other
, vanish. The least of these equations,
in connexion with equation (90a), contains Newton's theory of
gravitation. If we replace
by
we get
We see that the Newtonian gravitation constant
, is connected
with the constant
that enters into our field equations by the
relation
From the known numerical value of
, it therefore follows that
From (101) we see that even in the first approximation the structure
of the gravitational field differs fundamentally from that
which is consistent with the Newtonian theory; this difference
lies in the fact that the gravitational potential has the character
of a tensor and not a scalar. This was not recognized in the past
because only the component
, to a first approximation, enters
the equations of motion of material particles.
In order now to be able to judge the behaviour of measuring
rods and clocks from our results, we must observe the following.
According to the principle of equivalence, the metrical relations
of the Euclidean geometry are valid relatively to a Cartesian
system of reference of infinitely small dimensions, and in a suitable
state of motion (freely falling, and without rotation). We
can make the same statement for local systems of co-ordinates
[Pg 95]
which, relatively to these, have small accelerations, and therefore
for such systems of co-ordinates as are at rest relatively to
the one we have selected. For such a local system, we have, for
two neighbouring point events,
where
is measured directly by a measuring rod and
by
a clock at rest relatively to the system; these are the naturally
measured lengths and times. Since
, on the other hand, is
known in terms of the co-ordinates
employed in finite regions,
in the form
we have the possibility of getting the relation between naturally
measured lengths and times, on the one hand, and the corresponding
differences of co-ordinates, on the other hand. As the
division into space and time is in agreement with respect to the
two systems of co-ordinates, so when we equate the two expressions
for
we get two relations. If, by (101a), we put
we obtain, to a sufficiently close approximation,
[Pg 96]
The unit measuring rod has therefore the length,
in respect to the system of co-ordinates we have selected. The
particular system of co-ordinates we have selected insures that
this length shall depend only upon the place, and not upon the
direction. If we had chosen a different system of co-ordinates
this would not be so. But however we may choose a system of
co-ordinates, the laws of configuration of rigid rods do not agree
with those of Euclidean geometry; in other words, we cannot
choose any system of co-ordinates so that the co-ordinate differences,
,
,
, corresponding
to the ends of a unit measuring rod, oriented in any way,
shall always satisfy the relation
.
In this sense space is not Euclidean,
but "curved." It follows from the second of the relations above
that the interval between two beats of the unit clock (
= 1)
corresponds to the "time"
in the unit used in our system of co-ordinates. The rate of a
clock is accordingly slower the greater is the mass of the ponderable
matter in its neighbourhood. We therefore conclude that
spectral lines which are produced on the sun's surface will be
displaced towards the red, compared to the corresponding lines
produced on the earth, by about 2 • 10-6 of their wave-lengths.
At first, this important consequence of the theory appeared to
conflict with experiment; but results obtained during the past
year seem to make the existence of this effect more probable, and
[Pg 97]
it can hardly be doubted that this consequence of the theory will
be confirmed within the next year.
Another important consequence of the theory, which can be
tested experimentally, has to do with the path of rays of light.
In the general theory of relativity also the velocity of light is
everywhere the same, relatively to a local inertial system. This
velocity is unity in our natural measure of time. The law of
the propagation of light in general co-ordinates is therefore,
according to the general theory of relativity, characterized, by the
equation
To within the approximation which we are using, and in the
system of co-ordinates which we have selected, the velocity of
light is characterized, according to (106), by the equation
The velocity of light
, is therefore expressed in our co-ordinates
by
We can therefore draw the conclusion from this, that a ray of
light passing near a large mass is deflected. If we imagine the
sun, of mass
concentrated at the origin of our system of co-ordinates,
then a ray of fight, travelling parallel to the
-axis.
in the
plane, at a distance
from the origin, will be
deflected, in all, by an amount
[Pg 98]
towards the sun. On performing the integration we get
The existence of this deflection, which amounts to 1.7'' for
equal to the radius of the sun, was confirmed, with remarkable
accuracy, by the English Solar Eclipse Expedition in 1919, and
most careful preparations have been made to get more exact
observational data at the solar eclipse in 1922. It should be
noted that this result, also, of the theory is not influenced by
our arbitrary choice of a system of co-ordinates.
This is the place to speak of the third consequence of the theory which can be tested by observation, namely, that which concerns the motion of the perihelion of the planet Mercury. The secular changes in the planetary orbits are known with such accuracy that the approximation we have been using is no longer sufficient for a comparison of theory and observation. It is necessary to go back to the general field equations (96). To solve this problem I made use of the method of successive approximations. Since then, however, the problem of the central symmetrical statical gravitational field has been completely solved by Schwarzschild and others; the derivation given by H. Weyl in his book, "Raum-Zeit-Materie," is particularly elegant. The calculation can be simplified somewhat if we do not go back directly to the equation (96), but base it upon a principle of variation that is equivalent to this equation. I shall indicate the procedure only in so far as is necessary for understanding the method. [Pg 99]
In the case of a statical field, must have the form
where the summation on the right-hand side of the last equation
is to be extended over the space variables only. The central
symmetry of the field requires the
, to be of the form,
,
and
are functions of
only. One
of these three functions can be chosen arbitrarily, because our
system of co-ordinates is, a priori, completely arbitrary; for by
a substitution
we can always insure that one of these three functions shall be
an assigned function of
'. In place of (110) we can therefore
put, without limiting the generality,
In this way the are expressed in terms of the two quantities
and
. These are to be determined as functions of
,
by introducing them into equation (96), after first calculating
[Pg 100]
the
from (109) and (110a). We have
With the help of these results, the field equations furnish
Schwarzschild's solution:
in which we have put
denotes the sun's mass, centrally symmetrically placed
about the origin of co-ordinates; the solution (109) is valid only
outside of this mass, where all the
vanish. If the motion
of the planet takes place in the
plane then we
must replace (109a) by
[Pg 101]
The calculation of the planetary motion depends upon equation (90).
From the first of equations (110b) and (90) we get,
for the indices 1, 2, 3,
or, if we integrate, and express the result in polar co-ordinates,
From (90), for = 4, we get
From this, after multiplication by
and integration, we have
In (109c), (111) and (112) we have three equations between
the four variables ,
,
and
, from which the motion of the
planet may be calculated in the same way as in classical mechanics.
The most important result we get from this is a secular
rotation of the elliptic orbit of the planet in the same sense as
the revolution of the planet, amounting in radians per revolution
to
[Pg 102]
where
This expression furnishes the explanation of the motion of the
perihelion of the planet Mercury, which has been known for a
hundred years (since Leverrier), and for which theoretical astronomy
has hitherto been unable satisfactorily to account.
There is no difficulty in expressing Maxwell's theory of the
electromagnetic field in terms of the general theory of relativity;
this is done by application of the tensor formation (81), (82)
and (77). Let be a tensor of the first rank, to be denoted
as an electromagnetic 4-potential; then an electromagnetic field
tensor may be defined by the relations,
The second of Maxwell's systems of equations is then defined by
the tensor equation, resulting from this,
and the first of Maxwell's systems of equations is defined by the
tensor-density relation
[Pg 103]
in which
If we introduce the energy tensor of the electromagnetic field
into the right-hand side of (96), we obtain (115), for the special
case
= 0, as a consequence of (96) by taking the divergence.
This inclusion of the theory of electricity in the scheme of the
general theory of relativity has been considered arbitrary and
unsatisfactory by many theoreticians. Nor can we in this way
conceive of the equilibrium of the electricity which constitutes
the elementary electrically charged particles. A theory in which
the gravitational field and the electromagnetic field enter as an
essential entity would be much preferable. H. Weyl, and recently
Th. Kaluza, have discovered some ingenious theorems along this
direction; but concerning them, I am convinced that they do not
bring us nearer to the true solution of the fundamental problem.
I shall not go into this further, but shall give a brief discussion
of the so-called cosmological problem, for without this, the considerations
regarding the general theory of relativity would, in
a certain sense, remain unsatisfactory.
Our previous considerations, based upon the field equations (96), had for a foundation the conception that space on the whole is Galilean-Euclidean, and that this character is disturbed only by masses embedded in it. This conception was certainly justified as long as we were dealing with spaces of the order of magnitude of those that astronomy has to do with. But whether portions of the universe, however large they may be, are quasi-Euclidean, is a wholly different question. We can [Pg 104] make this clear by using an example from the theory of surfaces which we have employed many times. If a portion of a surface is observed by the eye to be practically plane, it does not at all follow that the whole surface has the form of a plane; the surface might just as well be a sphere, for example, of sufficiently large radius. The question as to whether the universe as a whole is non-Euclidean was much discussed from the geometrical point of view before the development of the theory of relativity. But with the theory of relativity, this problem has entered upon a new stage, for according to this theory the geometrical properties of bodies are not independent, but depend upon the distribution of masses.
If the universe were quasi-Euclidean, then Mach was wholly
wrong in his thought that inertia, as well as gravitation, depends
upon a kind of mutual action between bodies. For in this case,
with a suitably selected system of co-ordinates, the would
be constant at infinity, as they are in the special theory of relativity,
while within finite regions the
would differ from these
constant values by small amounts only, with a suitable choice
of co-ordinates, as a result of the influence of the masses in finite
regions. The physical properties of space would not then be
wholly independent, that is, uninfluenced by matter, but in the
main they would be, and only in small measure, conditioned by
matter. Such a dualistic conception is even in itself not satisfactory;
there are, however, some important physical arguments
against it, which we shall consider.
The hypothesis that the universe is infinite and Euclidean
at infinity, is, from the relativistic point of view, a complicated
hypothesis. In the language of the general theory of relativity
it demands that the Riemann tensor of the fourth rank
[Pg 105]
shall vanish at infinity, which furnishes twenty independent conditions,
while only ten curvature components
, enter into
the laws of the gravitational field. It is certainly unsatisfactory
to postulate such a far-reaching limitation without any physical
basis for it.
But in the second place, the theory of relativity makes it appear probable that Mach was on the right road in his thought that inertia depends upon a mutual action of matter. For we shall show in the following that, according to our equations, inert masses do act upon each other in the sense of the relativity of inertia, even if only very feebly. What is to be expected along the line of Mach's thought?
1. The inertia of a body must increase when ponderable masses are piled up in its neighbourhood.
2. A body must experience an accelerating force when neighbouring masses are accelerated, and, in fact, the force must be in the same direction as the acceleration.
3. A rotating hollow body must generate inside of itself a "Coriolis field," which deflects moving bodies in the sense of the rotation, and a radial centrifugal field as well.
We shall now show that these three effects, which are to be expected in accordance with Mach's ideas, are actually present according to our theory, although their magnitude is so small that confirmation of them by laboratory experiments is not to be thought of. For this purpose we shall go back to the equations of motion of a material particle (90), and carry the approximations somewhat further than was done in equation (90a). [Pg 106]
First, we consider as small of the first order. The square
of the velocity of masses moving under the influence of the gravitational
force is of the same order, according to the energy
equation. It is therefore logical to regard the velocities of the
material particles we are considering, as well as the velocities
of the masses which generate the field, as small, of the order
.
We shall now carry out the approximation in the equations that
arise from the field equations (101) and the equations of motion (90)
so far as to consider terms, in the second member
of (90), that are linear in those velocities. Further, we shall not
put
and
equal to each other, but, corresponding to the
higher approximation, we shall put
From (90) we obtain, at first,
From (101) we get, to the approximation sought for,
in which, in (117),
and
denote the space indices only.
[Pg 107]
On the right-hand side of (116) we can replace
1 + by 1
and
by
.
It is easy to see, in addition, that to this
degree of approximation we must put
in which
,
and
denote space indices.
We therefore obtain
from (116), in the usual vector notation,
The equations of motion, (118), show now, in fact, that
1. The inert mass is proportional to 1 + and therefore
increases when ponderable masses approach the test
body.
2. There is an inductive action of accelerated masses,
of the same sign, upon the test body. This is the
term .
[Pg 108]
3. A material particle, moving perpendicularly to the axis of rotation inside a rotating hollow body, is deflected in the sense of the rotation (Coriolis field). The centrifugal action, mentioned above, inside a rotating hollow body, also follows from the theory, as has been shown by Thirring.[18]
[18]That the centrifugal action must be inseparably connected with the existence of the Coriolis field may be recognized, even without calculation, in the special case of a co-ordinate system rotating uniformly relatively to an inertial system; our general co-variant equations naturally must apply to such a case.
Although all of these effects are inaccessible to experiment,
because is so small, nevertheless they certainly exist according
to the general theory of relativity. We must see in them a
strong support for Mach's ideas as to the relativity of all inertial
actions. If we think these ideas consistently through to the end
we must expect the whole inertia, that is, the whole
-field, to
be determined by the matter of the universe, and not mainly by
the boundary conditions at infinity.
For a satisfactory conception of the -field of cosmical dimensions,
the fact seems to be of significance that the relative
velocity of the stars is small compared to the velocity of light.
It follows from this that, with a suitable choice of co-ordinates,
is nearly constant in the universe, at least, in that part of
the universe in which there is matter. The assumption appears
natural, moreover, that there are stars in all parts of the universe,
so that we may well assume that the inconstancy of
depends
only upon the circumstance that matter is not distributed
continuously, but is concentrated in single celestial bodies and
systems of bodies. If we are willing to ignore these more local
[Pg 109]
non-uniformities of the density of matter and of the
-field, in
order to learn something of the geometrical properties of the universe
as a whole, it appears natural to substitute for the actual
distribution of masses a continuous distribution, and furthermore
to assign to this distribution a uniform density
. In this
imagined universe all points with space directions will be geometrically
equivalent; with respect to its space extension it will
have a constant curvature, and will be cylindrical with respect
to its
-co-ordinate. The possibility seems to be particularly
satisfying that the universe is spatially bounded and thus, in
accordance with our assumption of the constancy of
, is of
constant curvature, being either spherical or elliptical; for then
the boundary conditions at infinity which are so inconvenient
from the standpoint of the general theory of relativity, may be
replaced by the much more natural conditions for a closed surface.
According to what has been said, we are to put
in which the indices
and
run from 1 to 3 only.
The
will be such functions of
,
,
as correspond to
a three-dimensional continuum of constant positive curvature. We must
now investigate whether such an assumption can satisfy the field
equations of gravitation.
In order to be able to investigate this, we must first find
what differential conditions the three-dimensional manifold of
constant curvature satisfies. A spherical manifold of three dimensions,
[Pg 110]
embedded in a Euclidean continuum of four dimensions,[19]
is given by the equations
By eliminating
, we get
[19]The aid of a fourth space dimension has naturally no significance except that of a mathematical artifice.
As far as terms of the third and higher degrees in the , we
can put, in the neighbourhood of the origin of co-ordinates,
Inside the brackets are the of the manifold in the neighbourhood
of the origin. Since the first derivatives of the
,
and therefore also the
, vanish at the origin, the calculation
of the
for this manifold, by (88), is very simple at the origin.
We have
Since the relation
is universally co-variant,
and since all points of the manifold are geometrically equivalent,
this relation holds for every system of co-ordinates, and
everywhere in the manifold. In order to avoid confusion with
[Pg 111]
the four-dimensional continuum, we shall, in the following, designate
quantities that refer to the three-dimensional continuum
by Greek letters, and put
We now proceed to apply the field equations (96) to our special
case. From (119) we get for the four-dimensional manifold,
For the right-hand side of (96) we have to consider the energy
tensor for matter distributed like a cloud of dust. According to
what has gone before we must therefore put
specialized for the case of rest. But in addition, we shall add
a pressure term that may be physically established as follows.
Matter consists of electrically charged particles. On the basis
of Maxwell's theory these cannot be conceived of as electromagnetic
fields free from singularities. In order to be consistent
with the facts, it is necessary to introduce energy terms, not
contained in Maxwell's theory, so that the single electric particles
may hold together in spite of the mutual repulsions between
their elements, charged with electricity of one sign. For the sake
of consistency with this fact, Poincaré has assumed a pressure
[Pg 112]
to exist inside these particles which balances the electrostatic
repulsion. It cannot, however, be asserted that this pressure
vanishes outside the particles. We shall be consistent with this
circumstance if, in our phenomenological presentation, we add
a pressure term. This must not, however, be confused with a
hydrodynamical pressure, as it serves only for the energetic presentation
of the dynamical relations inside matter. In this sense
we put
In our special case we have, therefore, to put
Observing that the field equation (96) may be written in the
form
we get from (96) the equations,
From this follows
If the universe is quasi-Euclidean, and its radius of curvature
therefore infinite, then σ would vanish. But it is improbable that
[Pg 113]
the mean density of matter in the universe is actually zero; this
is our third argument against the assumption that the universe
is quasi-Euclidean. Nor does it seem possible that our hypothetical
pressure can vanish; the physical nature of this pressure can
be appreciated only after we have a better theoretical knowledge
of the electromagnetic field. According to the second of equations
(123) the radius, , of the universe is determined in terms
of the total mass,
, of matter, by the equation
The complete dependence of the geometrical upon the physical
properties becomes clearly apparent by means of this equation.
Thus we may present the following arguments against the conception of a space-infinite, and for the conception of a space-bounded, universe:—
1. From the standpoint of the theory of relativity, the condition for a closed surface is very much simpler than the corresponding boundary condition at infinity of the quasi-Euclidean structure of the universe.
2. The idea that Mach expressed, that inertia depends upon the mutual action of bodies, is contained, to a first approximation, in the equations of the theory of relativity; it follows from these equations that inertia depends, at least in part, upon mutual actions between masses. As it is an unsatisfactory assumption to make that inertia depends in part upon mutual actions, and in part upon an independent property of space, Mach's idea gains in probability. But this idea of Mach's corresponds only to a finite universe, bounded in space, and not to a quasi-Euclidean, infinite universe. From the standpoint of epistemology [Pg 114] it is more satisfying to have the mechanical properties of space completely determined by matter, and this is the case only in a space-bounded universe.
3. An infinite universe is possible only if the mean density of matter in the universe vanishes. Although such an assumption is logically possible, it is less probable than the assumption that there is a finite mean density of matter in the universe. [Pg 115]
A
Accelerated masses, inductive
action of, 108
Addition and subtraction of
tensors, 14
—theorem of velocities, 38
B
Biot-Savart force, 44
C
Centrifugal force, 64
Clocks, moving, 38
Compressible viscous fluid, 22
Concept of space, 3
—time, 28
Conditions of orthogonality, 7
Congruence, theorems of, 3
Conservation principles, 54
Continuum, four-dimensional, 31
Contraction of tensors, 14
Contra-variant vectors, 69
—tensors, 71
Co-ordinates, preferred systems
of, 8
Co-variance of equation of
continuity, 21
Co-variant, 12 et seq.
—vector, 68
Criticism of principle of inertia, 62
Criticisms of theory of
relativity, 29
Curvilinear co-ordinates, 65
D
Differentiation of tensors, 73, 76
Displacement of spectral lines, 97
E
Energy and mass, 45, 49
—tensor of electromagnetic
field, 50
—of matter, 54
Equation of continuity, co-variance
of, 21
Equations of motion of material
particle, 50
Equivalence of mass and
energy, 49
Equivalent spaces of reference, 25
Euclidean geometry, 4
F
Finiteness of universe, 105
Fizeau, 28
Four-dimensional continuum, 31
Four-vector, 41
Fundamental tensor, 71
G
Galilean regions, 62
—transformation, 27
Gauss, 65
Geodetic lines, 82
Geometry, Euclidean, 4
Gravitation constant, 95
Gravitational mass, 60
H
Homogeneity of space, 17
Hydrodynamical equations, 54
Hypotheses of pre-relativity
physics, 73
I
Inductive action of accelerated
masses, 108
Inert and gravitational mass, equality
of, 60
Invariant, 9 et seq.
Isotropy of space, 17
K
Kaluza, 104
L
Levi-Civita, 73
Light-cone, 41
Light ray, path of, 98
Light-time, 33
Linear orthogonal
transformation, 7
Lorentz electromotive force, 44
—transformation, 31
M
Mach, 59, 105, 106, 109, 114
Mass and Energy, 45, 49
—equality of gravitational and
inert, 60
—gravitational, 60
Maxwell's equations, 23
Mercury, perihelion of, 99, 103
Michelson and Morley, 28
Minkowski, 32
Motion of particle, equations of, 50
Moving measuring rods and
clocks, 38
Multiplication of tensors, 14
N
Newtonian gravitation
constant, 95
O
Operations on tensors, 13 et seq.
Orthogonal transformations, linear, 7
Orthogonality, conditions of, 7
P
Path of light ray, 98
Perihelion of Mercury, 99, 103
Poisson's equation, 87
Preferred systems of
co-ordinates, 8
Pre-relativity physics, hypotheses
of, 26
Principle of equivalence, 61
—inertia, criticism of, 62
Principles of conservation, 54
R
Radius of Universe, 113
Rank of tensor, 13
Ray of light, path of, 98
Reference, space of, 3
Riemann, 68
—tensor, 79, 82, 105
Rods (measuring) and clocks in
motion, 38
Rotation, 63
S
Simultaneity, 17, 29
Sitter, 28
Skew-symmetrical tensor, 15
Solar Eclipse expedition (1919), 99
Space, concept of, 2
—Homogeneity of, 17
—Isotropy of, 17
Spaces of reference, 3
—equivalence of, 25
Special Lorentz transformation, 34
Spectral lines, displacement of, 97
Straightest lines, 82
Stress tensor, 22
Symmetrical tensor, 15
Systems of co-ordinates,
preferred, 8
T
Tensor, 12 et seq., 68 et seq.
—Addition and subtraction of, 14
—Contraction of, 14
—Fundamental, 71
—Multiplication of, 14
—operations, 13 et seq.
—Rank of, 13
—Symmetrical and
Skew-symmetrical, 15
Tensors, formation by
differentiation, 73
Theorem for addition of
velocities, 38
Theorems of congruence, 3
Theory of relativity, criticisms
of, 29
Thirring, 109
Time-concept, 28
Time-space concept, 31
Transformation, Galilean, 27
—Linear orthogonal, 7
U
Universe, Finiteness of, 105
—Radius of, 113
V
Vector, co-variant, 69
—contra-variant, 69
Velocities, addition theorem of, 38
Viscous compressible fluid, 22
W
PRINTED IN GREAT BRITAIN AT THE UNIVERSITY PRESS, ABERDEEN
TRANSCRIBER'S NOTES
This ebook was produced using OCR text provided by Northeastern University's Snell Library through the Internet Archive.
Minor typographical corrections and presentational changes have been made without comment.